24 Hour Advance Forecast of Surface Ozone Using Linear and Non-Linear Models at a Semi-Urban Site of Indo-Gangetic Plain
Nidhi Verma, Sonal Kumari, Anita Lakhani and K Maharaj Kumari*
Department of Chemistry, Dayalbagh Educational Institute, India
Submission: February 23, 2019; Published: March 29, 2019
*Corresponding author: K Maharaj Kumari, Department of Chemistry, Faculty of Science, Dayalbagh Educational Institute, Dayalbagh, Agra 282110, India
How to cite this article: Nidhi V, Sonal K, Anita L, K Maharaj K. 24 Hour Advance Forecast of Surface Ozone Using Linear and Non-Linear Models at a Semi-Urban Site of Indo-Gangetic Plain. Int J Environ Sci Nat Res. 2019; 18(2): 555982. DOI:10.19080/IJESNR.2019.18.555982
Abstract
The present study includes prediction of next day hourly ozone concentration using four models viz. multiple linear regression (MLR), principal component regression (PCR), artificial neural network (ANN) and principal component based artificial neural network (PCANN). The input variables used for models construction were hourly concentration of previous day ozone, nitrogen dioxide (NO2), carbon monoxide (CO), temperature (T), relative humidity (RH), wind speed (WS), solar radiation (SR) and solar radiation duration (SRD). The measurement of ozone and its precursors was carried out at a semi-urban site of Dayalbagh, Agra. The models showed good agreement with observed levels of ozone. The value of regression coefficient ranged from 0.85 to 0.92 for different models. The highest value of regression coefficient was observed for PCANN model. In addition, normalized absolute error (NAE), root mean square error (RMSE), index of agreement (IA) and mean biased error (MBE) were also calculated to check the performance of different models. The principal component-based ANN model was the best model as it is associated with maximum value of regression coefficient (R = 0.92) and minimum value of errors. The efficiency of models was also checked for unknown datasets that were not used in model construction.
Keywords: Ozone; Multiple linear regression; Principal components; Artificial neural network; Errors
Abbrevations: MLR: Multiple Linear Regression; PCR: Principal Component Regression; ANN: Artificial Neural Network; PCANN: Principal Component based Artificial Neural Network; O3: Ozone; NO2: Nitrogen dioxide; CO: Carbon monoxide; T: Temperature; RH: Relative Humidity; WS: Wind speed; SR: Solar Radiation; SRD: Solar Radiation Duration; NAE: Normalized Absolute Error; RMSE: Root Mean Square Error; IA: Index of Agreement; MBE: Mean Biased Error
Introduction
Air pollution in urban areas has become a serious issue for developed as well as developing countries. Air pollution leads to both acute and chronic health effects [1,2]. Several studies have been conducted around the world on association of deteriorating air quality and daily mortality and morbidity [3-5]; therefore, control of air pollution is required. Among the harmful air pollutants, ozone has detrimental effects on human being as well as on vegetation. The short-term acute effects of ozone exposure include pulmonary dysfunction, irritation in airways and inflammation in the air passage [6]. Long-term exposure to humans causes worsening of previous respiratory diseases like asthma, dry throat, severe inflammation, persistent coughing and chest pain [7,8]. The critical level of O3 for human exposure is 90ppb for one hour according to NAAQS, CPCB, India [9] and equal to or greater than 70ppb for eight hours according to NAAQS, EPA [10].
Ozone levels at a site are influenced by precursor levels and meteorological conditions of the site. Although, the background levels of ozone are in the range of 20-35ppb but levels higher than 150ppb are also observed at various sites [11,12]. Several factors influence episodic levels of ozone that include high precursor levels, favourable meteorological conditions and poor circulation of air-masses. Therefore, if it is possible to predict these events one or two days in advance, it will be beneficial to human beings. The short-term forecasting is a significant step to take preventive actions during episodic events. Through these short-term forecasts, we can alert sensitive group of people (children, asthmatics and elderly people) and reduce the need of medication. Prediction of high ozone episodes using mathematical tools is very useful to provide early warning to the population. However, modelling of ozone levels is a complicated task as ozone has complex relationships with precursors and meteorological parameters [13].
Various air quality agencies have been working around the world to monitor air pollutants to forecast episodic events and to assess the impact of reduction in pollutants emission. To fulfil all these criteria and forecast pollutant levels several models have been employed. These models can be classified into two categories deterministic and statistical. Deterministic models are termed as cause and effect models; involve complex chemical reactions, transport and dispersion processes. These models are time consuming and need a large amount of dataset [14]. However, statistical models are quite simple and can be applied on real time data. In addition, deterministic models are suitable for large study areas and require accurate information of emission levels, transportation processes and meteorological conditions. However, statistical models can identify relationship of output variable with input variables without applying cause and effect analysis.
During the last decade several researchers have used various statistical techniques to analyze and forecast ozone levels including graphical analysis, fuzzy logics, multiple linear regression (MLR), principal component analysis (PCA), artificial neural networks (ANN) and combination of various methods [15-25]. MLR is a widely used statistical method in various fields like psychology, biology, medicine and environment [22,26,27]. PCA is considered as a useful tool to determine similarity in variables [23]. ANN has been suggested as the most appropriate statistical method for predicting the time series of different pollutants [28]. Several studies have used ANN as a viable approach for forecasting of O3, PM10, NO2, and NOx at different sites around the world [29,30].
In the present study, four models were constructed using MLR, PCR, ANN and PCANN. To model hourly ozone levels of next day, precursor concentrations (NO2 and CO), ozone levels and meteorological parameters viz. temperature (T), relative humidity (RH), solar radiation (SR), solar radiation duration (SRD) and wind speed (WS) of previous day were used as input variables.
Methodology
Study site and data
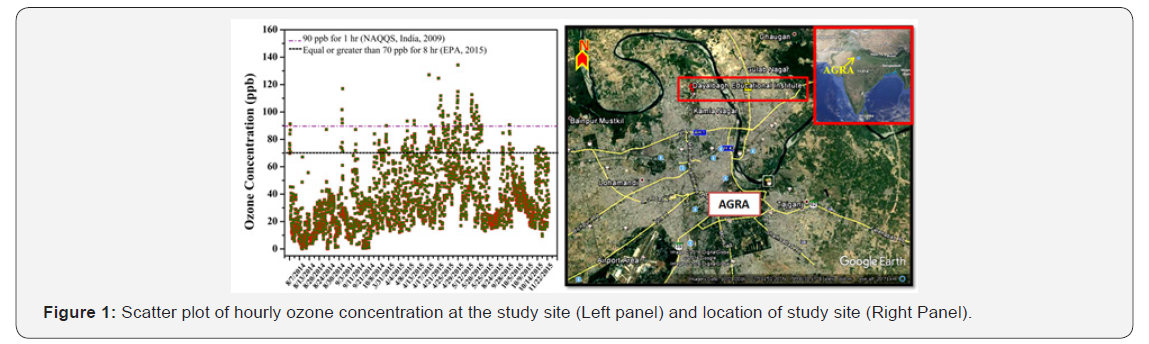
Trace gases (O3, NO2 and CO) measurements were carried out at the campus of Dayalbagh Educational Institute (semi-urban site), Agra (27°10´ N, 78°05´ E) located in North-central part of India. The location of sampling site in Agra is shown in Figure 1. The detailed description of the site has been discussed elsewhere [12]. O3, NOx and CO measurements were carried out using ozone (Thermo Scientific 49i), NOx (Thermo Scientific 42i) and CO analyzers (Teledyne T300), respectively. The ozone analyzer works on the principle of Lambert - Beer’s law. The ozone molecules show peak absorption at 254nm. NOx analyzer works on the principle of chemiluminescence by NO2 molecules which peak at nearly 630nm. The CO analyzer based on absorption of infra-red (IR) radiations at 4.67μm by CO molecules. The details on principles of these analyzers have been discussed elsewhere [12,31,32]. The detection limit of O3, NOx, and CO analyzer was 1.0ppb, 0.4ppb and < 0.04ppm respectively. Zero and span calibrations of these analyzers were done on a weekly basis using zero air generator and dynamic gas calibrator (Teledyne T700).
Meteorological parameters viz. temperature, relative humidity, solar radiation, solar radiation duration and wind speed were recorded at the sampling site using Automatic Weather Station WM271 Data Logger at one-hour interval.
Models
Four models were constructed using MLR, PCR, ANN and PCANN. Statistical Packages for Social Sciences 16.0 (SPSS 16.0) was used for MLR and PCR while MATLAB R2013a was used for ANN analysis.
Model 1: Multiple Linear Regression (MLR)
Multiple linear regression (MLR) establishes a linear relationship between a dependent variable and more than one independent variables [33]. The general equation of MLR can be expressed by the formula given below:
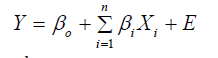
where,
Y = Response variable (O3(d+1))
βo = Constant
βi= Coefficients of explanatory variables
Xi= explanatory variables viz. O3, NO2, CO, temperature, relative humidity, solar radiation, solar radiation duration and wind speed.
E= Error associated with the model regression.
MLR depends on linear and additive coalition of independent explanatory variables. MLR is based on following assumptions:
(i) The variables should be independent in nature and
(ii) Normal distribution of the residual errors. Normal distribution is associated with zero mean and constant variance [34]. However, MLR is often associated with multicollinearity which indicates dependence of two or more explanatory variables on one another. It can be determined using tolerance value; a tolerance of less than or equals to 0.5 indicates multicollinearity is a problem, a tolerance of 0.30 or less indicates a serious multicollinearity problem [35].
Model 2: Principal Component Regression (PCR)
PCR is a combined method of PCA and MLR. In this method principal components generated through PCA are used as input variables to reduce multicollinearity and to make model simple. As these selected PCs were associated with high loadings and can explain majority of original variables, therefore they are ideal for the use in MLR [36].
Principal Component Analysis (PCA): Principal Component Analysis (PCA) is a useful multivariate statistical method to explain the variance of a complex set of correlated variables. PCA transforms them into small number of independent variables termed as principal components (PCs) [37]. PCs are linear combination of original variables and they are orthogonal to each other [16]. PCA has ability to identify most significant variable and can omit least significant variables without affecting the original data [38]. In PCA, Bartlett’s test of sphericity is applied to check whether variables are correlated to each other or not. Kaiser-Meyer- Olkin (KMO) test verifies the applicability of PCA on the dataset and KMO value >0.5 indicates suitability of data for PCA. Varimax rotation was applied which makes the model simple by making small loadings smaller and large loadings larger and it assures that each variable has maximum correlation with only one principal component and minimally correlated with other variables [37].
Model 3: Artificial Neural Network (ANN)
As the relationship of O3 with its precursors and meteorological variables is non-linear in nature therefore, nonlinear models like ANN can predict O3 levels efficiently as compared to linear models [21]. The feedforward backpropagation network is commonly used to resolve nonlinear problems [38]. This network consists of three layers: input layer, hidden layer and output layer. These three layers remain connected to each other through neurons or nodes, these neurons can exchange information with all other neurons of layers. The output value of a neuron is obtained by applying an activation function viz. sigmoid, hyperbolic tangential or linear. Earlier studies have suggested that there is no strict rule to design the architecture of network [39,40]. The number of neurons in input layer is equal to the number of input variables. The most common problems in designing architecture of hidden layer includes number of neurons and suitable activation function. The optimum number of neurons in hidden layer is required because small number of neurons may lead to underfitting while large number of neurons may lead to overfitting of the model. According to Yang et al. [41], number of neurons in hidden layer can be determined by using formula:
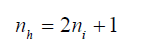
where, nh is number of neurons in hidden layer while ni is number of neurons in input layer. In the present study, linear (purelin) and hyperbolic tangent sigmoid (transig) activation functions were used [39,42]. The overfitting problem in ANN was avoided using cross-validation test which involves data testing on one subgroup and its validation on the other [40].
Model 4: Principal Component based Artificial Neural Network (PC-ANN)
For PC-ANN model, principal components are used as input variables instead of original variables. Therefore, the model has less complex architecture and might be more efficient in predicting ozone levels.
Performance Indicators
The errors and accuracies of developed models can be evaluated using performance indicators like NAE (Normalized Absolute Error), RMSE (Root Mean Square Error), IA (Index of Agreement), MBE (Mean Biased Error) and coefficient of determination (R2) [34].
a) NAE: Normalized absolute error is summation of difference of predicted and measured value divided by summation of observed values.
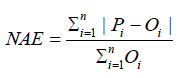
b) RMSE: Root mean square error indicates success of prediction of models. RMSE is defined by the formula:

c) IA: Index of Agreement measures how accurately models are working and given by the formula [43].
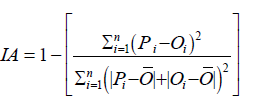
IA values have a range of 0 to 1. IA equals to 0 indicates that predicted and observed values have no agreement while IA equals to 1 indicates that there is perfect correlation between observed and predicted values.
d) MBE: Mean biased error indicates degree of over or under prediction. MBE value > 0 is an indicator of over prediction while < 0 value is an indicator of under prediction.
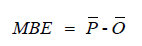
where, Oi = Observed concentration, Pi = Predicted concentration, O = mean of observed concentration, P = mean of predicted concentration, n = number of data points.
In this study datasets of 2014-2015 were used for model’s construction (data for those days when value of any variable was missing for more than six hours was removed). Therefore, 2400 datasets were selected for the study. The complete dataset was normalized before using it in different models. The efficiencies of all the models were also checked by using an unknown dataset which was not included in the construction of these models. The unknown dataset was around 25% of the total data used.
Results and Discussion
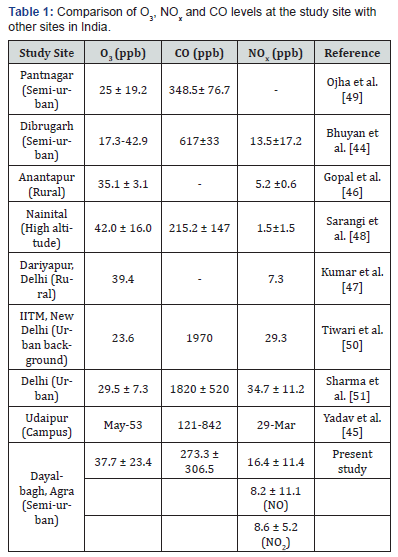
The comparison of average concentration of O3, NOx and CO at the study site with other sites in India is shown in Table 1 [44,45]. The levels of O3 at the study site were moderate and comparable with a rural site (35.1 ± 3.5ppb) of Anantapur [46] and a rural site (39.4ppb) of Delhi [47] while lower (42.0 ± 16.0ppb) than a high-altitude site of Nainital [48]. The average O3 concentration at the study site was higher than a semi-urban site of Pantnagar [49], an urban background site of New Delhi [50] and an urban site of Delhi [51]. NOx levels were higher than a rural site of Anantapur, a rural site of Delhi, a high-altitude site of Nainital and a semi-urban site of Dibrugarh. However, CO levels at the study site were lower than other sites except high altitude site, Nainital. At the study site, hourly ozone levels frequently exceed air quality standards provided by CPCB, India (2009) (O3 > 90 ppb for one hour) and EPA (2015) (O3 levels ≥ 70 ppb for eight hours) (Figure 1). The days when ozone exceeds air quality standards may be termed as ozone episodes [12]. These high ozone episodes may cause detrimental effects on sensitive group of people and crops.
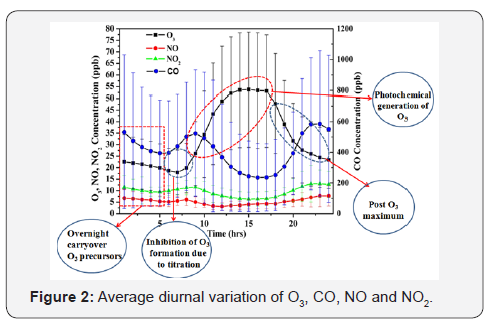
Ozone levels are significantly influenced by precursor levels, meteorological conditions and topography of the site as it is a secondary pollutant [52]. Figure 2 shows the diurnal pattern of ozone, NO, NO2 and CO. The average diurnal pattern of ozone was characterized by minimum value of 17.9±9.7ppb during early morning hours (~7:00h), reached a maximum value of 53.7±24.9ppb during afternoon (~15:00h), remained steady until ~17:00h, and then decreased until next morning. The night time low levels of ozone can be attributed to absence of photochemical generation and titration with NO. The diurnal variation of ozone can be classified into four phases as shown in Figure 2. During the first phase (01:00-05:00h), there was a slow decrease in ozone and its precursor levels. The second phase lies in between 06:00h to 08:00h when ozone generation was inhibited by NO and NO2 generated from photolysis of night time accumulated NO3˙ and N2O5. The third phase was the photochemical generation of ozone during 09:00 h to 17:00h and the rate of ozone formation was high during these hours. The last phase was post maximum phase which started after 17:00h. During this phase, levels of ozone fall as loss by NO, NO2 and deposition was fast in the descended boundary layer.
To find out the relationship of ozone with its precursors and meteorological parameters, Pearson correlation analysis was performed. Table 2 shows results of correlation analysis among hourly data of O3(d+1), O3, NO2, CO, T, RH, WS, SR and SRD. The next day hourly ozone concentration showed strong positive correlation with ozone concentration, temperature and solar radiation duration of previous day and strong negative correlation with relative humidity. The O3(d+1) levels also showed moderate positive correlation with solar radiation and negative correlation with NO2. Significant positive correlation of ozone with temperature and solar radiation suggest role of photochemistry in surface ozone formation. O3(d+1) showed negative correlation with its precursors NO2 and CO. The negative correlation with wind speed suggests that high wind speed causes dilution of air and may result in low levels of O3.

*-Correlation is significant at p<0.001

FS = Factor Scores.
Model 1: Multiple linear regression (MLR)
In the present study, stepwise multiple linear regression was used which can determine the contribution of different variables to predictive equation. The histogram plot for residuals was normalized in nature. Model summary is shown in Table 3 which gives value of multiple correlation R, R2, adjusted R2 and equation of best fit model which has maximum R2. The R2 is also known as coefficient of determination which explains the fraction of variation in the dependent variable explained by overall regression model [53]. The higher value of R2 indicates that model fits well with data. R2 defines that variation of dependent variable is explained by all the independent variables, however, adjusted R2 is a measure of variation of dependent variable explained by only those independent variables that affect the dependent variable [20].
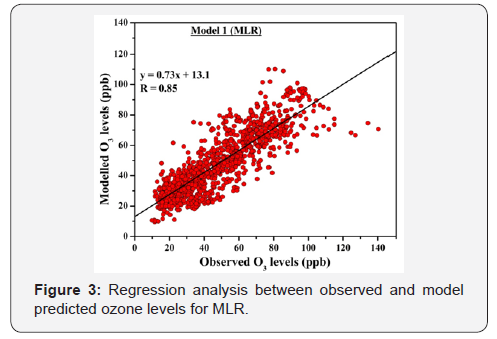
In Table 3, coefficients used in MLR equation are for normalized dataset which suggests that ozone levels of the next day are maximally influenced by previous day hourly ozone levels. In the regression equation CO and SRD were not included as predictors by the model because their variation was not statistically significant (p>0.01). A significant positive regression coefficient (R=0.85) was observed between measured and modelled values as shown in Table 3 and Figure 3. The tolerance value was less than 0.5 for O3 (0.491), NO2 (0.482) and T (0.454).
Model 2: Principal component regression (PCR)
As discussed in introduction section that PCR is a combination of PCA and MLR, therefore, we first applied PCA on the whole dataset. PCA is useful for selecting variables for MLR [54]. The limitation of multicollinearity associated with MLR can be avoided using PCA.
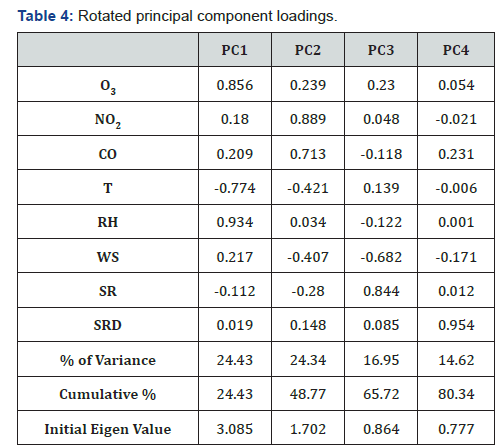
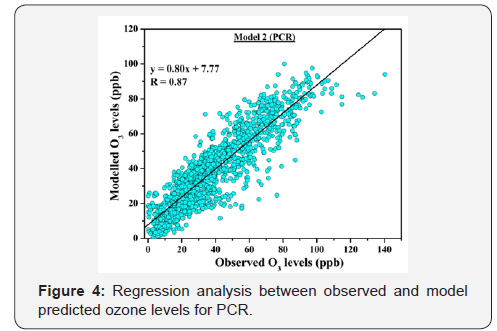
Principal component analysis (PCA): The varimax rotation was applied and the main objective of PCA is to get small number of components which can explain maximum variation. Bartlett’s sphericity test was applied to verify the usability of PCA in the data- set used and it was significant (p < 0.001), therefore, the data is applicable for PCA. The KMO value was also greater than 0.5 which also indicates suitability of data for PCA. According to Kaiser criterion, PCs with eigen value equal or greater than one is usually retained for the analysis, however, Izenman [55] suggested that PCs with eigen value greater than or equal to 0.7 are also statistically significant. He et al. [56] also followed the similar criteria in their study. Following this criterion, four PCs were selected for the present study (Table 4). Table 4 shows loadings associated with four PCs. The first four PCs explain 80.34% of variance. On first PC, O3, temperature and RH have significant loadings and it explains 24.43% of variation in independent variables. Second PC explains 24.34% of variance and it is heavily loaded on NO2 and CO. The third PC is heavily loaded on wind speed and solar radiation; and explains 16.95% variance. The fourth PC has significant positive loading on solar radiation duration. As four principal components are selected for the study therefore corresponding four factor scores are also saved by the model which can be further utilized as input variables in MLR analysis [16,17]. Table 3 shows R, R2 and adjusted R2 which are better for Model 2 as compared to Model 1. The regression coefficient between observed and predicted value was 0.87 (Figure 4).
Model 3: Artificial neural network (ANN)
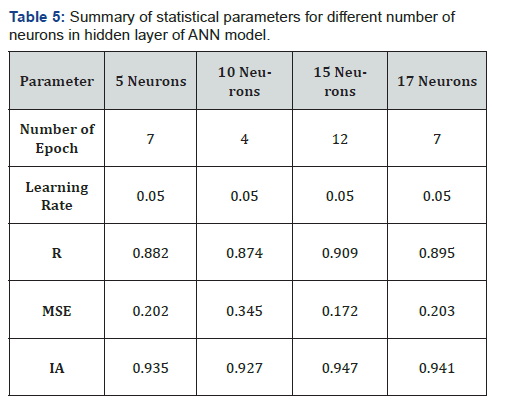
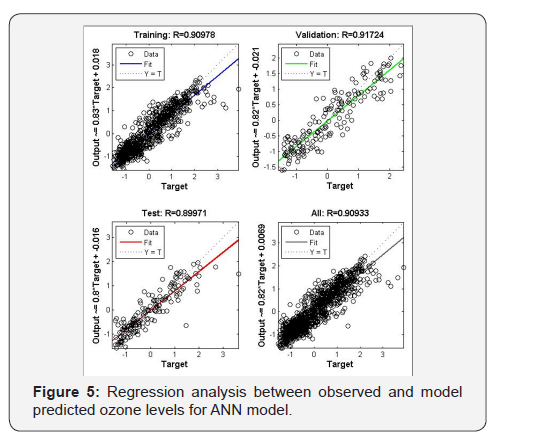
Model 3 is a feedforward back-propagation ANN model which consists of three layers: input, hidden and output layer. The Levenberg Marquardt backpropagation method was used for the model construction. There are eight input variables and one output variable, therefore, eight and one neuron were selected in input and output layer, respectively. The number of neurons in hidden layer affects model’s efficiency far greater as compared to number of hidden layers [57]. Following the approach of Yang et al. [41] optimum number of neurons in hidden layer was 17 (ni = 8). The model was optimized for best performance by using different numbers of neurons in hidden layer. Here, we are showing the results of model output for 5, 10, 15 and 17 neurons in hidden layer (Table 5). The ANN model with 15 neurons in hidden layer showed maximum correlation (R = 0.91) with the observed levels. This model was associated with minimum value of mean square error (MSE) (0.172), maximum number of epochs (12) and highest value of index of agreement (IA) (0.947). Therefore, the model with 15 neurons is considered as optimized model. Although the value of regression coefficient increases with further increase in number of hidden layer neurons (nh = 20, 25 and so on) but the error also increases. Figure 5 shows regression analysis between observed and model predicted ozone levels for training, testing and validation dataset. The whole dataset was partitioned into 70% of training, 15% of validation and 15% of testing dataset. For training, validation and testing datasets regression coefficients were 0.91, 0.92 and 0.89, respectively. The overall regression coefficient was 0.91.
Model 4: Principal component-based ANN model (PCANN)
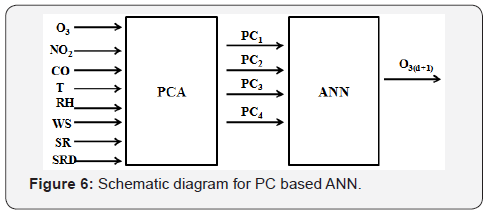

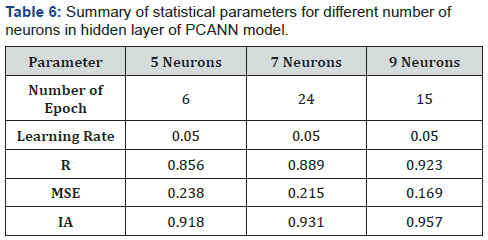
The model 3 can be simpler and more efficient if principal components are used as input variables instead of all eight variables because PC based ANN model is devoid of multicollinearity. The construction of model was initiated by the application of PCA analysis on input variable like model 2. Therefore, four principal components were generated, and, on these PCs, ANN was applied. The basic structure of PC-ANN is shown in Figure 6. Figure 6 shows that eight variables were used to generate four PCs which can explain most of the variance in the original variables and were used as input variables in ANN. Therefore, input layer is consisted of four neurons and optimum number in hidden layer is 9 (2ni +1) [41]. The efficiency of the model was again checked by considering different number of neurons in hidden layer. Table 6 shows variation in statistical parameters by taking 5, 7 and 9 neurons in hidden layer. The transig and purelin activation function were used. The PCANN model with 9 neurons in hidden layer showed maximum correlation (R = 0.92) with the observed levels. This model was associated with minimum value of MSE (0.169) and the highest value of IA (0.957). For PCANN model, the dataset was partitioned into training (70%), validation (15%) and testing dataset (15%). The regression coefficients for training, validation and testing datasets were 0.89, 0.92 and 0.87. The overall regression coefficient was 0.92 (Figure 7).
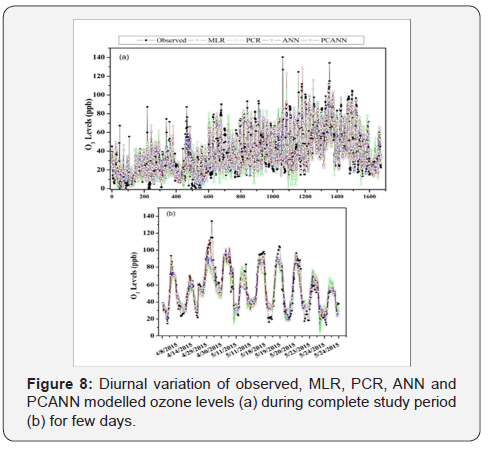
Figure 8 (a) shows time series of observed ozone levels and model predicted ozone levels during the study period while Figure 8 (b) shows diurnal variation of ozone only for few days to describe efficiency of various models in explaining the diurnal variation of ozone. As shown in Figure 8(b) most of the days MLR underestimates ozone levels during peak ozone hours while overestimates its levels during early morning and late-night hours. ANN and PCANN showed good agreement with observed data, however, extent of correlation is better for PCANN. On the other hand, all the models are not able to predict sudden rise in ozone levels. In the present study, other precursors of ozone like nonmethane hydrocarbons (NMHCs) and meteorological parameters like wind direction were not considered hence the efficiency of these models can be improved by using them as input variables. In addition, ozone levels are driven by complex set of chemical reactions therefore it is difficult to predict its exact concentrations.
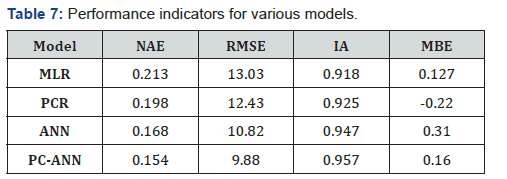
The performance of all these models were assessed using various error terms like normalized absolute error, root mean square error, index of agreement and mean biased error. Table 7 shows values of performance indicators for all models. The value of NAE was the maximum for MLR based model followed by PCR, ANN and PC-ANN models. Similarly, RMSE was the maximum for MLR model and the minimum for PC-ANN model. The value of NAE and RMSE should be closer to zero for the most accurate model [51].
RMSE gives the estimate of overall deviation between observed and predicted values. The low value of RMSE indicates that model is working well [34]. However, high value of RMSE does not mean that model is completely wrong because peak values have high impact on RMSE [58]. IA is an indicator of closeness of observed and predicted value. If the model is closer to one it indicates that predicted values are close to observed values and it was closest to 1 for PC-ANN based model indicating best agreement of this model with observed dataset. The value of MBE was less than zero for PCR while greater than zero for MLR, ANN and PCANN which suggest that MLR, ANN and PCANN were over predicting ozone levels while PCR showed under prediction.
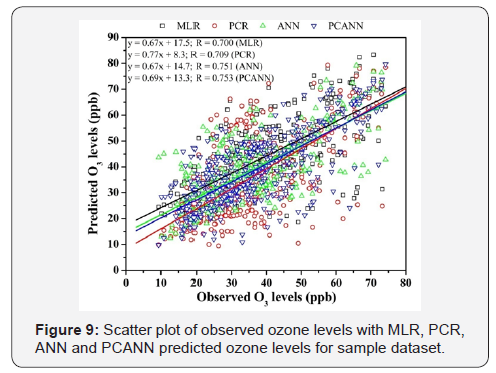
Figure 9 shows regression analysis of predicted ozone and observed ozone levels for sample dataset. This sample dataset was not used for construction of models. For multiple linear regression, the regression coefficient between observed and predicted data was 0.7 while for PCR regression coefficient was 0.709. The value of regression coefficient for ANN (R = 0.751) and PC-ANN (R = 0.753) was slightly higher. The R value for sample data set was smaller than that of modelled data. The models were optimized for the dataset used for their construction and not for sample data which may result in decrease in accuracy for sample data.
Conclusion
The study includes prediction of next day hourly ozone concentration using four models. These models are multiple linear regression (MLR), principal component regression (PCR), artificial neural network (ANN) and principal component-based ANN (PCANN). These models were constructed using hourly concentration of O3, NO2, CO, temperature, relative humidity, wind speed, solar radiation and solar radiation duration of 2014-2015. During the study period, the average concentration of O3, NO2 and CO was 37.7±23.4, 8.6±5.2 and 273.3±306.5ppb, respectively. At the study site, ozone levels exceed hourly and eight hourly NAAQS ozone limit on several days which may result in detrimental effect on human health and vegetation, therefore, prediction of ozone levels is an essential requirement.
The first model is based on MLR and regression coefficient for this model was 0.85. The equation for the model suggests that O3 levels of next day maximally influenced by previous day hourly O3 levels. The second model was PCR model which was constructed by using factor scores of principal components (PCs) as input variable in multiple linear regression. For these four principal components were generated through principal component analysis. The regression coefficient for second model (R = 0.87) was better than first model as it is devoid of problem of multicollinearity. The model 3 is feedforward backpropagation ANN model consisted of three layers. The best model has 15 neurons in hidden layer and regression coefficient of 0.909. The model 4 is principal component- based ANN model. Like model 2 in this model, factor scores of four PCs were used as input variables. The best model is consisted of 9 neurons in hidden layer and has regression coefficient of 0.923. The R value is significantly higher for nonlinear models (ANN and PCANN) as compared to linear models (MLR and PCR).
The performance of all models was checked using various error terms. Based on error terms, the best model was PCANN as it is associated with minimum value of NAE, RMSE and maximum value of IA. The efficiency of model was also checked using an unknown dataset which was not used in the construction of models. All the models showed satisfactory agreement between observed and predicted O3 levels.
Acknowledgment
The authors are thankful to the Director, Dayalbagh Educational Institute, Agra and the Head, Department of Chemistry for necessary help. The authors gratefully acknowledge the financial support for this work which was provided by ISRO GBP under AT-CTM project.
References
- Kim KH, Kabir E, Kabir S (2015) A review on the human health impact of airborne particulate matter. Environ Int 74: 136-143.
- Turnock ST, Butt EW, Richardson TB, Mann GW, Reddington CL, et al. (2016) The impact of European legislative and technology measures to reduce air pollutants on air quality, human health and climate. Environ Res Lett 11(2): 024010.
- Dimitriou K, Paschalidou AK, Kassomenos PA (2013) Assessing air quality with regards to its effect on human health in the European Union through air quality indices. Ecol Indic 27: 108-115.
- Ogwu FA, Peters AA, Aliyu HB, Abubakar N (2015) An Investigative approach on the effect of air pollution on climate change and human health in the niger delta region of Nigeria. Int J Sci Res Innov Technol 2(5): 37-49.
- Tedoldi D, Chebbo G, Pierlot D, Branchu P, Kovacs Y, et al. (2017) Spatial distribution of heavy metals in the surface soil of source-control stormwater infiltration devices–Inter-site comparison. Sci Total Environ 579: 881-892.
- Moustris KP, Nastos, PT, Larissi IK, Paliatsos AG (2012) Application of multiple linear regression models and artificial neural networks on the surface ozone forecast in the greater Athens area, Greece. Adv. Meteorol 2012(894714): 8.
- Nastos PT, Paliatsos AG, Anthracopoulos MB, Roma ES, Priftis KN (2010) Outdoor particulate matter and childhood asthma admissions in Athens, Greece: a time-series study. Environ Health 9(1): 45.
- Samoli E, Nastos PT, Paliatsos AG, Katsouyanni K, Priftis KN (2011) Acute effects of air pollution on pediatric asthma exacerbation: evidence of association and effect modification. Environ Res 111(3): 418-424.
- NAAQS, CPCB (2009) The gazette of India, ministry of environmental and forests notification. National Ambient Air Quality Standards 16.
- NAAQS, EPA (2015) Criteria pollutants.
- Saavedra S, Rodríguez A, Taboada JJ, Souto JA, Casares JJ (2012) Synoptic patterns and air-mass transport during ozone episodes in northwestern Iberia. Sci Total Environ 441: 97-110.
- Verma N, Lakhani A, Kumari KM (2017a) High ozone episodes at a semiurban site in India: Photochemical generation and transport. Atmos Res 197: 232-243.
- Borrego C, Schatzmann M, Galmarini S (2003) Quality assurance of air pollution models. In Air Quality in Cities, Springer Berlin Heidelberg, USA, pp. 155-183.
- Zanetti M, Litteri L, Gennaro R, Horstmann H, Romeo D (1990) Bactenecins, defense polypeptides of bovine neutrophils, are generated from precursor molecules stored in the large granules. J Cell Biol 111(4): 1363-1371.
- Abdul-Wahab SA, Al-Alawi SM (2002) Assessment and prediction of tropospheric ozone concentration levels using artificial neural networks. Environ Modell Softw 17(3): 219-228.
- Abdul-Wahab SA, Bakheit CS, Al-Alawi, SM (2005) Principal component and multiple regression analysis in modelling of groundlevel ozone and factors affecting its concentrations. Environ Modell Softw 20(10):1263-1271.
- Al-Alawi SM, Abdul-Wahab SA, Bakheit CS (2008) Combining principal component regression and artificial neural networks for more accurate predictions of ground-level ozone. Environ Modell Softw 23(4): 396- 403.
- Feng Y, Zhang W, Sun D, Zhang L (2011) Ozone concentration forecast method based on genetic algorithm optimized back propagation neural networks and support vector machine data classification. Atmos Environ 45(11): 1979-1985.
- Gocheva-Ilieva SG, Ivanov AV, Voynikova DS, Boyadzhiev DT (2014) Time series analysis and forecasting for air pollution in small urban area: an SARIMA and factor analysis approach. Stoch Environ Res Risk Assess 28(4): 1045-1060.
- Lengyel A, Héberger K, Paksy L, Bánhidi O, Rajkó R (2004) Prediction of ozone concentration in ambient air using multivariate methods. Chemosphere 57(8): 889-896.
- Moustris KP, Ziomas IC, Paliatsos AG (2010) 3-Day-ahead forecasting of regional pollution index for the pollutants NO2, CO, SO2, and O3 using artificial neural networks in Athens, Greece. Water Air Soil Pollut 209(1-4): 29-43.
- Özbay B, Keskin GA, Doğruparmak ŞÇ, Ayberk S (2011) Multivariate methods for ground-level ozone modeling. Atmos Res 102(1-2): 57-65.
- Sousa SIV, Martins FG, Alvim-Ferraz MCM, Pereira MC (2007) Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations. Environ Modell Softw 22(1): 97-103.
- Singla V, Pachauri T, Satsangi A, Kumari KM, Lakhani A (2012) Surface ozone concentrations in Agra: links with the prevailing meteorological parameters. Theor Appl climatol 110(3): 409-421.
- Verma N, Satsangi A, Lakhani A, Kumari KM (2015) Prediction of ground level ozone concentration in ambient air using multiple linear regression. J Chem Biol Phy Sci 5(4): 3685-3696.
- Ansiau D, Marquié JC, Soubelet A, Ramos S (2005) Relationships between cognitive characteristics of the job, age, and cognitive efficiency. In International Congress Series, Elsevier 1280: 43-48.
- Smith CM, Wachob DG (2006) Trends associated with residential development in riparian breeding bird habitat along the Snake River in Jackson Hole, WY, USA: implications for conservation planning. Biol Cons 128(4): 431-446.
- Gardner MW, Dorling SR (1998) Artificial neural networks (the multilayer perceptron)—a review of applications in the atmospheric sciences. Atmos Environ 32(14-15): 2627-2636.
- Dutot AL, Rynkiewicz J, Steiner FE, Rude J (2007) A 24-h forecast of ozone peaks and exceedance levels using neural classifiers and weather predictions. Environ Modell Softw 22(9): 1261-1269.
- Papanastasiou DK, Melas D, Kioutsioukis I (2007) Development and assessment of neural network and multiple regression models in order to predict PM10 levels in a medium-sized Mediterranean city. Water Air Soil Pollut 182(1-4): 325-334.
- Singla V, Pachauri T, Satsangi A, Kumari KM, Lakhani A (2011) O3 Formation and Destruction at a Sub-urban Site in North Central Region of India. Atmos Res 101(1-2): 373-385.
- Verma N, Satsangi A, Lakhani A, Kumari KM, Lal S (2017b) Diurnal, Seasonal, and Vertical Variability in Carbon Monoxide Levels at a Semi‐ Urban Site in India. CLEAN 45(5).
- Pires JCM, Martins FG, Sousa SIV, Alvim-Ferraz MCM, Pereira MC (2008) Selection and validation of parameters in multiple linear and principal component regressions. Environ Modell Softw 23(1): 50-55.
- Vlachogianni A, Kassomenos P, Karppinen A, Karakitsios S, Kukkonen J (2011) Evaluation of a multiple regression model for the forecasting of the concentrations of NOx and PM10 in Athens and Helsinki. Sci Total Environ 409(8): 1559-1571.
- Janssen W, Wijnen K, Pelsmacker PD, Kenhove PV (2008) Marketing Research with SPSS. Pearson Education Limited, UK.
- Gvozdić V, Kovač-Andrić E, Brana J (2011) Influence of meteorological factors NO2, SO2, CO and PM10 on the concentration of O3 in the urban atmosphere of Eastern Croatia. Environ Modell Assess 16(5): 491-501.
- Dominick D, Juahir H, Latif MT, Zain SM, Aris AZ (2012) Spatial assessment of air quality patterns in Malaysia using multivariate analysis. Atmos Environ 60: 172-181.
- Ul-Saufie AZ, Yahaya AS, Ramli NA, Rosaida N, Hamid HA (2013) Future daily PM10 concentrations prediction by combining regression models and feedforward backpropagation models with principle component analysis (PCA). Atmos Environ 77: 621-630.
- Elbayoumi M, Ramli NA, Yusof NFFM (2015) Spatial and temporal variations in particulate matter concentrations in twelve schools environment in urban and overpopulated camps landscape. Build Environ 90: 157-167.
- Chellali MR, Abderrahim H, Hamou A, Nebatti A, Janovec J (2016) Artificial neural network models for prediction of daily fine particulate matter concentrations in Algiers. Environ Sci Pollut Res 23(14): 14008-14017.
- Yang J, Rivard H, Zmeureanu R (2005) On-line building energy prediction using adaptive artificial neural networks. Energy Build 37(12): 1250-1259.
- Kriesel D (2007) A Brief Introduction to Neural Networks, (1st edn).
- Yusof NFFM, Ramli NA, Yahaya AS, Sansuddin N, Ghazali NA, et al. (2010) Monsoonal differences and probability distribution of PM10 concentration. Environ Monitor Assess 163(1-4): 655-667.
- Bhuyan PK, Bharali C, Pathak B, Kalita G (2014) The role of precursor gases and meteorology on temporal evolution of O3 at a tropical location in northeast India. Environ Sci Pollut Res 21(10): 6696-6713.
- Yadav R, Sahu LK, Beig G, Jaaffrey SN (2016) Role of long-range transport and local meteorology in seasonal variation of surface ozone and its precursors at an urban site in India. Atmos Res 176-177: 96- 107.
- Gopal KR, Lingaswamy AP, Arafath SM, Balakrishnaiah G, Kumari SP, et al. (2014) Seasonal heterogeneity in ozone and its precursors (NOx) by in-situ and model observations on semi-arid station in Anantapur (AP), South India. Atmos Environ 84: 294-306.
- Kumar A, Singh D, Singh BP, Singh M, Anandam K, et al. (2015) Spatial and temporal variability of surface ozone and nitrogen oxides in urban and rural ambient air of Delhi-NCR, India. Air Qual Atmos Health 8(4): 391-399.
- Sarangi T, Naja M, Ojha N, Kumar R, Lal S, et al. (2014) First simultaneous measurements of ozone, CO, and NOy at a high‐altitude regional representative site in the central Himalayas. J Geophys Res Atmos 119(3): 1592-1611.
- Ojha N, Naja M, Singh KP, Sarangi T, Kumar R, et al. (2012) Variabilities in ozone at a semi‐urban site in the Indo‐Gangetic Plain region: Association with the meteorology and regional processes. J Geophys Res Atmos 117(D20).
- Tiwari S, Dahiya A, Kumar N (2015) Investigation into relationships among NO, NO2, NOx, O3, and CO at an urban background site in Delhi, India. Atmos Res 157: 119-126.
- Sharma A, Sharma SK, Mandal TK (2016) Influence of ozone precursors and particulate matter on the variation of surface ozone at an urban site of Delhi, India. Sustain Environ Res 26(2): 76-83.
- Naja M, Lal S (2002) Surface ozone and precursor gases at Gadanki (13.5°N, 79.2°E), tropical rural site in India. J Geophys Res 107(D14): ACH 8-1-ACH 8-13.
- Bowerman BL, O’Connell RT, Koehler AB (2005) Forecasting Times Series, and regression. An Applied Approach (4th edn), Belmont, CA: Thomson Learning, USA.
- Awang NR, Ramli NA, Yahaya AS, Elbayoumi M (2015) Multivariate methods to predict ground level ozone during daytime, nighttime, and critical conversion time in urban areas. Atmos Pollut Res 6(5): 726- 734.
- Izenman AJ (2008) Modern multivariate statistical techniques (Chapter 7.2). Springer, New York, USA.
- He HD, Lu WZ, Xue Y (2015) Prediction of particulate matters at urban intersection by using multilayer perceptron model based on principal components. Stoch Environ Res Risk Assess 29(8): 2107-2114.
- Abderrahim H, Chellali MR, Hamou A (2016) Forecasting PM10 in Algiers: efficacy of multilayer perceptron networks. Environ Sci Pollut Res 23(2): 1634-1641.
- Willmott CJ (1981) On the validation of models. Phys Geography 2(2): 184-194.






























