Horacio E Cristiani*; Maricruz Oviedo

doi:10.19080/GJO.2018.17.555969

Research Article

Auditory Synaptopathy and Masking Psychometric Function Slope: A Conjecture

**Horacio E Cristiani* and Maricruz Oviedo**

Mutualidad Argentina de Hipoacúsicos, Buenos Aires, Argentina hc, Argentina

Submission: September 05, 2018; Published: September 17, 2018

*Corresponding author: Horacio E Cristiani, Mutualidad Argentina de Hipoacúsicos, Argentina.

How to cite this article: Horacio E C, Maricruz O . Auditory Synaptopathy and Masking Psychometric Function Slope: A Conjecture. Glob J Oto, 2018; 17(4):555969. DOI: 10.19080/GJO.2018.17.555969

Abstract

Kujawa and Liberman showed in laboratory animals that, because of exposure to noise doses that do not produce a permanent displacement of the thresholds, synapse destruction occurs between the internal hair cells (IHC) and the fibers of the auditory nerve (ANF). Studies were proposed to confirm this result in humans and estimate the perceptual effects that this type of dysfunction (called Hidden Hearing Loss) could cause. The decrease in the number of synapses would mainly affect the neurons of high threshold and low spontaneous firing rate, being less affected the low threshold and high spontaneous firing rate. The effect of this type of loss should be detected in situations of speech detection with background noise, in particular with high levels of such noise. A summary is presented with some of the previous knowledge on auditory synaptopathy and a rationale about a method to detect these hidden losses in subjects with normal hearing and hearing impaired is conjectured. The proposed method is based on the comparison of the slope of the psychometric curves of signal to noise ratio, obtained in high frequency, for different levels of masking noise.

Keywords: Synaptopathy; Hidden Hearing Loss; Psychometric Function; Psychoacoustics

Abbrevations: IHC: inner hair cells; HHL: Hidden Hearing Losses

Introduction

From the revealing work of [1], which showed the existence of “hidden” hearing losses, a change in the auditory system as a result of the damage at the synapses between the inner hair cells (IHC) and the fibers of the auditory nerve (ANF) called Synaptopathy a great amount of effort was generated looking for confirmation of its existence in humans and to estimate the perceptual effects that this type of dysfunction could cause [2-4]. It has also been speculated about the efficiency that different methods, both objective and behavioral, could provide in an attempt to achieve a differential diagnosis of this type of auditory deficit [2,5-9]. Synaptopathy occurs by exposure to noise and also as a natural part of aging and is not detected in pure tone audiometry, therefore, many people can have hearing damage without being diagnosed. While this type of exposure does not have permanent consequences for outer (OHCs) and inner hair cells (IHCs), it mainly damages the synapses corresponding to low-spontaneous rate fibers that are involved in the processing of high level sounds, which they are less resistant to the masking produced by background noise. This hearing losses are referenced as “Hidden” because, although the loss of synapses is immediate, it is not seen in routine histological studies and the subsequent loss of cells of the spiral ganglion takes months and even years (due to the loss of trophic factors generated by supporting cells in areas of IHC).

On the other hand, neural degeneration is selective for high threshold fibers, which, despite not being required in silence (for audiometric thresholds), are critical for listening in noisy environments. In the experiments carried out by Kujawa and Liberman, mice exposed to noise doses that do not cause a permanent shift of the auditory threshold, but do produce a temporary shift, showed a decrease in the count of synapses between the inner hair cells and the fibers of the auditory nerve. The animals studied had displacements in their auditory thresholds, which could be measured through ABR and OEAs. These displacements were of a transitory nature, since after two weeks the thresholds resumed their initial values, however the post-mortem count of synapses of these same animals showed significant differences with non-exposed animals. This decrease in the number of synapses would preferentially take place in the fibers of high threshold and low spontaneous rate, being less affected the low level and high spontaneous rate. This last distinction between the groups of fibers that are affected explains why these hearing losses are not revealed in a standard audiometry.

For that reason they are named “Hidden Hearing Losses” (HHL). The effect of this type of loss should be more noticeable in speech situations with background noise, and especially with high levels of noise. This type of exposure does not have permanent damage for external (OHCs) or internal hair cells (IHCs) but it produce damage to the synapses corresponding to low spontaneous fibers that are involved in the processing of high level sounds, which are less resistant to masking that produces background noise. The fibers of the auditory nerve, mostly (60- 80%) have low threshold and high rate of spontaneous activity in the absence of noise, while a small percentage, between 20- 40% correspond to the high threshold and low spontaneous rate, the latter being the most vulnerable to noise. Fibers of low spontaneous response rate do not contribute to the detection of silent thresholds but by means of their high thresholds they are the key to the encoding of transient stimuli in the presence of background noise that saturates the response of high spontaneous rate fibers.

This observation suggests that the loss of fibers of low spontaneous response rate would be the major contributor in the difficulty of speech discrimination in noisy environments. In this work a summary with some of the previous knowledge on the auditory synaptopathy is showed and a conjecture is presented and explained with a mathematic model that can give results that could help on the diagnosis of these hidden losses in subjects with normal hearing and hearing impaired. The comparison of the slope in the psychometric curves of the signal to noise ratio in high frequency, for different levels of masking noise is introduced as a method to help in the diagnostic of this kind of hearing loss.

Basic Concepts

Sensorineural hearing damage can occur as a result of dysfunction in one or more of these four components:

a) Outer hair cells (OHCs)

b) Inner hair cells (IHCs)

c) Synapses between the IHCs and the auditory nerve

d) Fibers of the auditory nerve (ANFs)

The loss or damage of external hair cells brings, among other consequences, the elevation of the auditory thresholds, which is easily revealed in standard audiometry. The same does not occur with the other components, whose damage estimation is not always possible by current methods in the clinic [10]. Developed a test with a special type of masking noise called Threshold Equalizing Noise (TEN): a fast and reliable method to detect regions of the cochlea where the IHCs are missing or dysfunctional. These are called “cochlear dead regions” [10]. The damage in the IHCs is not clearly detectable in a pure tone audiometry because the tones with frequencies whose characteristic frequency (CF) falls within a cochlear region that has lost their IHCs are still detectable by the hair cells of cochlear regions located in other healthy areas (phenomenon known as “off frequency listening”).

This method, as presented by the authors, is less expensive in terms of time, than another classic alternative to evaluate the existence of dead regions: the determination of Psychophysical Tuning Curves (PTCs) [10]. Auditory neuropathy can have origin anywhere from the synaptic transmission to the action potentials conduction in the ANFs. Although auditory neuropathy is classified as a subclass of sensorineural hearing loss, it is considered infrequent. It is characterized by the correct functioning of OCHs and ICHs but abnormal responses ABR (with normal acoustic otoacoustic emissions, negative ABR, normal pure tone audiometry and reduced speech discrimination). There has been a consensus that hair cells are the primary target of noise, the “main victim”, and that the damage of sensory neurons, if it exists, it is secondary.

Lab experiments with animals have suggested that the damage to the synapses induced by noise exposure appears even before the damage in the OHCs and the IHCs and this could explain the existence of hidden hearing losses [1]. Some authors suggest that the survival of the ANFs depends on the neurotrophins of the supporting cells in areas of the IHCs, even in the absence of the latter. In case the hair cells survival, neurotrophin therapy could elicit dendritic growth of spiral ganglion neurons and thus restore the synapses. Although the loss of synapses from noise exposure occurs several hours later, the degeneration of cochlear neurons may take years or decades. Therefore, there could be a therapeutic possibility whereby sensory cells and neurons would be reconnected. Indeed, recent animal studies reported regeneration of the synapse between the IHCs and ANFs after exposure to noise with functional recovery, using neurotrophinbased therapy, either through genetic overexpression or through local neurotrophics factor administration directly in the round window [9]. These studies suggest that OHCs and IHCs are not the elements affected at first in the inner ear. Synapses are the first to be damaged as a result of aging or noise exposure. This neural degeneration does not change auditory thresholds, but it is very likely to produce poorer discrimination in noisy environments. As a result of experiments they showed that at noise exposures that cause a temporary threshold shift (TTS) of between 35 and 45 dB, but not a permanent shift (the latter verified by measuring thresholds by objective methods, after two weeks), cause an immediate synaptopathy in the first 24 hours. This synaptopathy is visualized as a loss of between 40% and 50% of the synapses in the area of the IHC. At the same time there is no evidence of loss of IHCs or OHCs. Despite this loss of synapses, both ABR and DPOAE thresholds are fully recovered, indicating the temporal nature of the hearing loss. Although the eventual loss of the SGN is very slow, the loss of an ANF as a result of exposure to noise renders this fiber useless.

In the original work by Kujawa and Liberman, no evidence of synapse regeneration was found, and an even greater loss of synapses could be demonstrated over time in the exposed mice. In terms of the temporary threshold shifts, this research showed that the basal part is more vulnerable than the apical part of the cochlea. The fact that a loss of synapses can take place without damage to the hair cells does not mean that both kinds of hearing damages are mutually exclusive. Most likely, there is always a component of synaptopathy accompanying cochlear loss, when we refer to losses induced by noise or the effect of aging. Bearing in mind that the primary consequence of noise exposure (the one that chronologically appears first) is precisely the synaptic degeneration, the loss in hair cells may appear later. Therefore, the loss in the synapses may not be alone. Instead, it can be a companion of the dysfunction in the OHCs and IHCs. So there may be a “hidden” component that is added to the component of hearing loss showed in an audiogram.

This hidden component could explain some of the differences in the percentages of speech discrimination if we compare subjects with similar hearing losses or the uneven performance with hearing aids in people fitted with similar technologies and equal audiometric profiles: perhaps one of them adds up to a greater amount of the hidden component. As Ridley (2018) points out, in a group of people with identical audiograms, whether they are normal or hearing impaired, the performance in suprathreshold tests may be different due to the existence of this hidden component [10]. Showed that the total hearing loss can be considered formed by two components, each one attributable to a group of cells (outer and inner).

HLOHC + HLIHC = HLTOTAL (1)

Although it is not possible to separate the specific amounts corresponding to each type of loss by means of audiometric techniques, the detection of cochlear dead regions can provide frequency information regarding where the regions with greater loss due to dysfunction in the IHCs would be located. To these components of hearing loss, which brings less sensitivity, and can be measured through a pure tone audiometry (and separated in terms of its two components through the TEN test), another one could be added, which does not produce differences in the auditory threshold itself, but it would have a negative impact on supra threshold signal detection in noisy environments. We will call this HHL and we will not include it explicitly in equation (1) since this component does not produce an increase in the audiometric thresholds. When Moore describes dead regions he explain them as generically “cochlear regions”, that is, he places them in the IHCs. But when he goes into more detail, he talks about “internal hair cells in certain places of the basilar membrane that can be completely nonfunctional, and also the auditory afferent neurons that innervate these places can be non-functional” [10] and ends by saying: “We refer to the places (of the BM) with IHC’s non-functional neurons as dead regions. “Therefore Moore includes two different entities in the definition of dead regions, the IHCs and the neurons. When we talk about synaptopathy we are talking about only one of them.

As known, each IHC has in average 10 synapses with neurons of the afferent system, so the loss of synapses would produce the same effect as the dead cochlear region only if all the synapses corresponding to a given IHC were damaged. If only some of them are damaged there would still be a link to the auditory nerve. If IHCs are safe, as may be the case after exposure to noise that causes a transient threshold shift, but synapses corresponding to low spontaneous rate and high threshold have damage and those of low threshold remain safe, this would not affect the audiometric thresholds, but would bring poorer speech discrimination in noisy environments. Thus, the difference between a synaptopathy and a dead region is that in the first case, at the threshold level, it is these same IHCs that capture the stimulus, while in the case of the dead region the stimulus is captured outside of frequency, by means of IHCs from other cochlear regions (Off- frequency listening).

Porposals for the Diagnostic of Synaptopathy

The experiments of [1] have shown that noise exposure that does not produce permanent threshold changes can induce an appreciable and permanent decrease in the number of synapses between the IHCs and the auditory nerve. However, the existence of this same pattern in humans could not yet be demonstrated directly, although [11] found loss of synapses in post-mortem studies in elderly humans, without reported hearing deficit, with an almost normal amount of hair cells. In the attempts of finding evidence of hidden hearing loss in humans, several studies can be carried out to evaluate the integrity of the system along the stimulus path, through objective (DPOAE’s, ABR) or behavioral (psychoacoustic) methods to detect and recognize the specific responses of OHCs, IHCs, synapses and ANFs. As synaptopathy would mainly affect the ANFs nerve of low spontaneous and high threshold rate (LSR), the method must be able to evaluate them in some differential way {12]. Reviewed the approaches faced by various authors to achieve a diagnosis of this type of loss. We add some other proposals. First of all, the ones based on electrophysiological measurements:

a) ABR: Amplitude decrease of Wave I (Action Potential) at high levels of stimulation

b) FFR: Reduction in the synchrony to frecuency modulation.

c) Relationship between summation potential and the action potential (SP/AP rate).

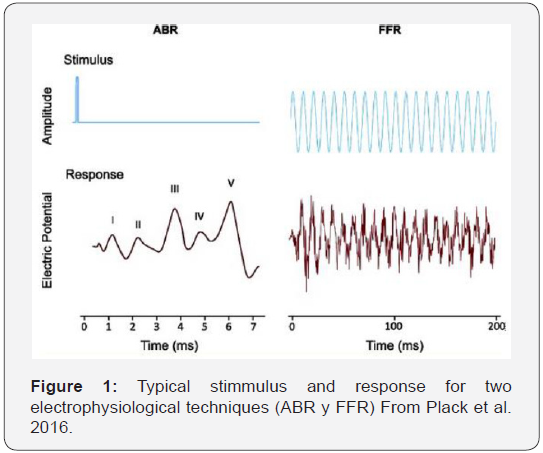
The technique of ABRs evoked by clicks has the advantage of objectivity: it is relatively easy to find and measure Wave I, which reflects the function of the auditory nerve (Figure 1) [1]. Found that after exposure to noise the amplitude of Wave I is reduced at moderate to high levels, but has no changes at low levels, suggesting a selective loss of fibers of low spontaneous rate (LSR). Even more important is the fact that the amplitude of wave I in these studies has a high correlation with the population of non affected synapses. This provides a validation for this model in rodents. In humans, the question is less evident, but both in the case of aging and in the case of noise exposure, a reduction in the amplitude of the Wave I for high-level clicks has been demonstrated.

In addition, this amplitude of the Wave I for high level clicks does not translate into wave V amplitude reduction in patients with tinnitus, due to an increase in the compensatory central gain [12,13]. However, there are some problems arising from the use of ABR for the diagnosis of HHL, because in humans Wave I has relatively low amplitude and shows a wide variability intra and inter subjects (Beattie, 1988, Lauter & Loomis, 1988). Therefore, the variability in the amplitude of the Wave I may be the result not only of a synaptopathy but of another number of factors totally different to it, such as, for example, sex, head size, variations in synchronization, external noise, physiological, etc. So, although measurements of Wave I allow demonstrating group differences, for example, between groups of exposed subjects and those not exposed to noise, they would not be useful to determine whether or not a particular individual has a hidden component. In addition, the amplitude of Wave I evoked by a click (broad band) is strongly influenced by activity in basal regions of the cochlea. Although conventional audiometry was normal in the clinical range up to 8 KHz, the loss of hair cells in regions corresponding to higher frequencies would also have an influence on the results, which would make it necessary to cancel the possible effect of the more basal regions, by means of adequate low-pass filtering.

The second proposed technique, FFR (Frequency Following Response) shows the neural activity in the synchronized cortex phase locked to the stimulus wave. This is a more robust measure than the amplitude of the Wave I. There is some evidence that FFR can predict the performance in frequency and modulation discrimination experiments, which would be affected by synaptopathy. The drawback of this method is that the FFR potential occurs at the cortical level, mainly in the inferior colliculus area (Krishan, 2006), so its characteristics are influenced by the central activity. In addition, like Wave I it shows great intra and inter subject variability. Figure 1 shows the shape of the stimuli and the expected response [2].

The third procedure [6] is based on the hypothesis that the rate of growth of the Compound Action Potential (CAP) will be lower in cochlear regions with auditory synaptopathy due to exposure to noise. The results are encouraging, as they found a relationship between this fall in the growth rate and the risk factors evaluated (basically low performance in speech discrimination tests in noise). The relationship between the Summating Potential (SP) and the Action Potential AP (SP / AP) has been proposed by Liberman et al. as a good measure to quantify the degree of neural loss, useful for the diagnosis of hidden hearing losses. The analysis of the electrocochleograms suggests a significant difference between the peaks of the waves generated by the hair cells (Summating Potential, SP) and those generated by the cochlear neurons (Action Potential, AP).

Psychoacoustics and Synaptopathy

One of the expected consequences of auditory synaptopathy is the loss of performance in detection tasks of signals in the presence of background noise. More specifically, it has been speculated that hidden hearing losses, although they do not bring visible effects in a standard pure tone audiometry, could explain some deficits in speech discrimination in the presence of noise, but it is not easy to determine if the performance decrease found in those experiments are caused by perceptual factors or central processing disorders. That is, the response to these psychophysical tests is impregnated with numerous factors and does not allow to discern the origin of the different observable behaviors. Although there is evidence that subjects with a history of noise exposure but with normal audiograms have difficulties in speech perception and temporal processing (Alvord, 1983; Kumar, Ammendin, Sangamanatha, 2012), it is uncertain whether these problems are the result of a synaptopathy or other type of dysfunction, for example of the IHCs or central processing disorders.

The same occurs with the deficits in speech perception and temporal processing due to aging: although they have been confirmed [14], (Rajan, Crainer, 2002) it is not possible to detect their exact origin [12]. Points out that psychophysical measurements, such as obtaining thresholds, require a response from the subject and therefore potentially reflect the state of the complete path from peripheral hearing to the finger that press a key or a button to give the answer. Then one can consider that the answers will be influenced by factors not related to the synaptopathy like memory and attention, among others [3]. Performs an analysis through a model based on Signal Detection Theory (Green & Sweets, 1950), to predict the possible perceptual consequences of synaptopathy and concludes that an appreciable loss of synapses would produce changes in noise detection thresholds that result too small to be measured reliably. Following the work of [15] who calculated the amount of auditory nerve fibers required to achieve certain levels of intensity discrimination, based on the properties of an individual neuron, Oxenham determined that with a loss in the count of synapses as significant as 50%, the sensitivity d’ would be reduced by a factor of just √2.

This would lead to a threshold increase of only 1.5 dB which is too small to be measured with a high degree of reliability. But the same author points out that this analysis is based on three simplifications: it consider the fibers response to be independent between them, it assumes that fiber information is optimally combined and also consider that all fibers carry the same information, so that a functional loss of fibers does not depend on what type of fibers are damaged. These conclusions are based on a model of how information about the fibers of the auditory nerve is combined. This model also assumes that the synapse loss is evenly distributed, when in fact it is believed that it mainly affects the fibers of low spontaneous rate and also in a specific region of the cochlea [12]. Concludes that psychoacoustic experiments performed at high levels in the region of the affected frequencies could have the necessary sensitivity. He also points out that the performance of some psychoacoustic experiments may be inherently more sensitive to synaptopathy, especially those related to temporal processing, such as modulation detection.

Differential Measurements for Synaptopathy Detection

Trying to find evidence of synaptopathy in humans finds an important stumbling block in the variability of measurable characteristics, both inter and intra subjects. One approach that would minimize both types of variability is to use a differential measurement, in which two measures are compared for an individual, one supposed to be affected by the synaptopathy and the other that is considered not affected. Both measures should also be affected by other forms of variability, in such a way that it would be minimized or canceled altogether. A procedure of this type would be adequate in both physiological and psychophysical tests and would at least reduce or eliminate the influence of central processing factors [12]. points out that there are at least two approaches for differential measurements of synaptopathy, based on the characteristics of the stimulus:

a) Comparisons changing the level

b) Comparisons changing the frequency

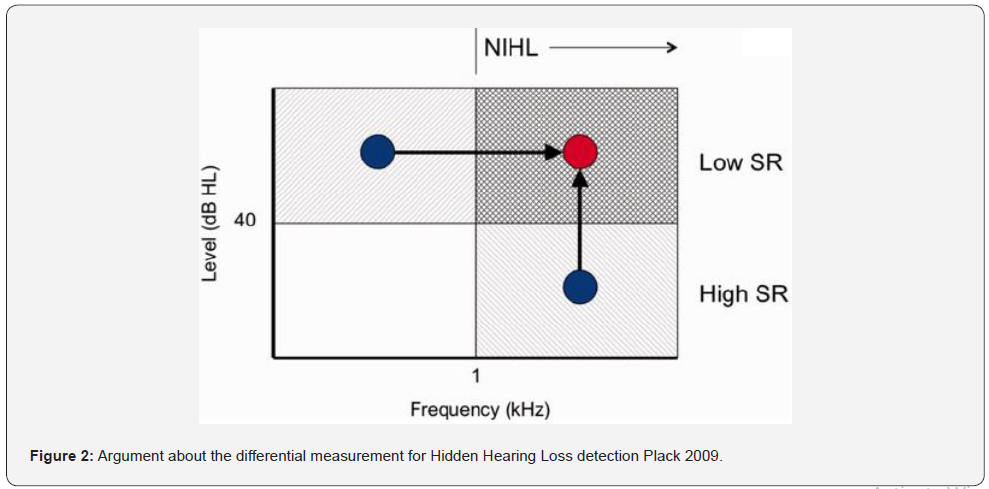
It is believed that synaptopathies preferentially affect fibers with low spontaneous rate, so their effects should be observed at high levels of stimulus. On the other hand, noise-induced hearing losses affect the sensitivity at high frequencies preferably, so it is postulated that synaptopathies should affect the region of high level and high frequency more noticeably. Figure 2 [12] shows the logic behind the use of differential methods for the detection of synaptopathy. Since the fibers with low spontaneous rate (LSR) and high threshold would be affected, the effects should be noticeable at a high level and since noise-induced hearing losses (NIHL) occur mainly at high frequencies, the shaded area is where alterations should be found, and we can perform comparison experiments from the regions indicated with the points (high level and low frequency or high frequency low level), compared to high frequency, high level. Figure 2 Argument about the differential measurement for Hidden Hearing Loss detection [12].

Following this approach, [8] proposes an interesting method based on the measurement of auditory thresholds with background noise and its comparison with auditory thresholds without background noise by correlation analysis. It is postulated that the residual of the correlation can provide a quantitative measure of the degree of hidden hearing loss, because it represents the portion of the variance in the thresholds in noise, which does not depend on the thresholds in silence, but is only evident in a supraliminal measure of auditory function [8]. The procedure for the identification of the hidden component of loss, which can be assigned to the auditory synaptopathy, make the comparison of the residue of the correlation between the thresholds measured with background noise [10] and the silent thresholds at 1KHz and 4 KHz. This work is important, because it tries to find an evidence of synaptopathy that is based on psychoacoustic experimentation. Another attempt to reveal this type of hearing loss through behavioral tasks is based in detection with binaural masking [16]. The approach proposed in the present work is based on the analysis of the effect that synaptopathy can produce in the slope of the psychometric curve of signal-to-noise ratio, for high stimulus values.

The Psychometric Function (FP)

The psychometric function Figure 3 shows the relationship between the magnitude of a stimulus and its detection probability. In this case stimulus value is the signal-to-noise ratio (SNR), the sound level difference (expressed in dB) between a test tone and the background noise. The ability to detect the presence of a test tone in the presence of a masking noise has been widely studied in the literature. The magnitude of the stimulus (or variable independent of the FP) is in our case the SNR and is shown on the abscissa. The dependent variable as in all FP, is the percentage of detection represented in the ordinate axis.

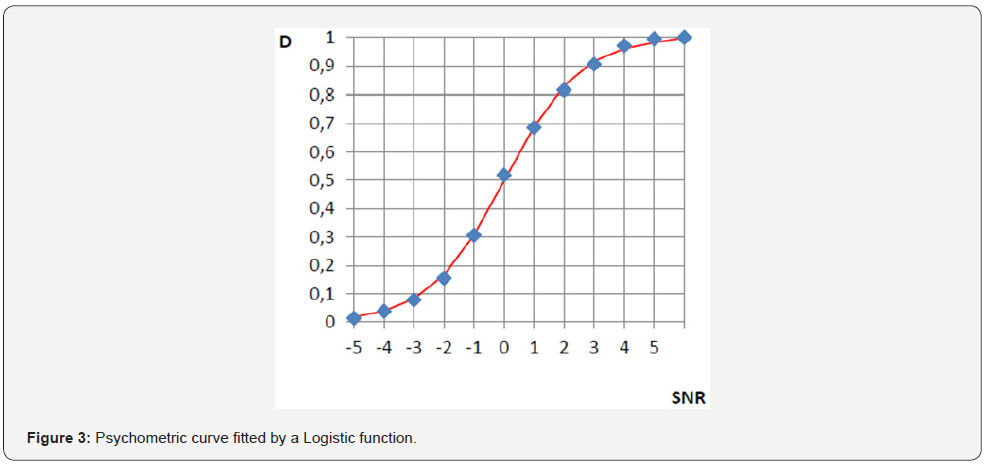
Figure 3 shows a typical psychometric function, where D corresponds to the detection % divided by 100, such that when the stimulus is detected 100% of the presentations, D = 1. The points on the graph show the different values obtained in an experiment of this type. These values are subsequently fitted to obtain the function. The most used fitting are Weibull and Logistic function, the latter is expressed by:

Here x is the value of SNR in dB, β is the slope of the function and α is related to the threshold. The threshold is defined as the value of the stimulus (x = u) for which D = 0.5 thus:

Considering logarithm in both members:

We obtain the threshold value:

The slope is given by β / 4 and shows the growth rate of the PF with increase of the SNR. The theoretical understanding of the characteristics of the psychometric function and how to interpret variations in its threshold and slope is a way for the exploration of a neuronal alteration such as synaptopathy. In the case of stimulus detection experiments, there has been a theoretical research framework that accounts for the meaning of the psychometric curve, both in the visual and the auditory domain. The individual sensory neurons show response functions (rate-level) that closely resemble the psychometric function, and an approximation to the interpretation of psychophysical data is to establish a summation of probabilities model among the sensory units [17]. In the case of patterns recognition, both visual and auditory, the same author recognizes that we are far from this model of psychometric function. The reason is that it is not yet clear how to make a model that includes the combination of low level sensory information in the pattern recognition process. Then, an eminently empirical and descriptive point of view is taken, without giving special meaning to the characteristics of the psychometric curve [17]. Gold and Ding (2013) proposed a model that explains the way decision mechanisms affect the shape of the psychometric curve, both in Yes-No and 2AFC procedures. Hence, the result of psychophysical experiments can be related, that is, “perceptual sensibility” with “neurometric sensitivity”.

The slope of the psychometric curve describes the reliability in the performance of the subject, for the different values of stimulus, but particularly in the measurement of the threshold. One of the first attempts to interpret the slope of the psychometric function in terms of the neural mechanisms focused on problems of contrasts detection. In an experiment of this kind, an ideal observer with complete knowledge of all the relevant parameters of the stimulus should, in principle, present a sensitivity that grows linearly as a function of the contrast. The reduction of the masking effect in low spontaneous rate and high threshold fibers is understood based on its two main characteristics: high threshold and high dynamic range. Low threshold neurons reach saturation with low stimulus levels and do not work for the differential detections required at a high level (as they have already reached saturation). In contrast, the high threshold (and low spontaneous rate) fibers are useful at high level because they have that differential response capacity.

The slope of the psychometric function shows the subject’s incremental ability to improve its detection rate when the stimulus value is increased. Several authors have shown the necessary association of the psychometric curve and the response to the stimulus of an individual neuron [18]. The presented analysis is intended to show that the dysfunction of low spontaneous rate and high threshold fibers can be reflected in the slope of the psychometric curve for high levels of signal and noise. The aim of the proposed experiments is to evaluate the ability to detect tonal stimuli of different intensity ranges, masked with narrow band noise, at different values of signal-to-noise ratio (SNR). The parameter that serves as intensity is here the SNR. A neuron permanently stimulated with noise is in such an excited state that it will result in a certain base firing rate. The superposition of the tonal stimulus requires, to be detected, an increase in that firing rate. The ratio between the stimulus increments and the firing rate is the slope of this neurometric curve, which will in turn be reflected in the psychometric function. At a low level of stimulation, the neurons of high spontaneous and low threshold are the main “contributors of slope” to the psychometric curve, those of low threshold and high spontaneous rate either have not yet reached their threshold or are in a region of the stimulus range where they have not yet reached their maximum contributions to the slope. On the other hand, for high values of the stimulus, the neurons of high spontaneous rate are already saturated, being those of low spontaneous and high threshold that contribute to the slope. The absence or decrease of these fibers should then translate into a fall in the slope of the psychometric function, with respect to that obtained for low stimulus levels, where the intact fibers of high spontaneous rate would act. It would then be useful to evaluate the complete psychometric curve and not simply the threshold and adjust the curves obtained to obtain information their thresholds and slopes. The conjecture presented here suggests that the failure in low spontaneous and high threshold neurons should be appreciated in the variation of the slope of the psychometric function of signal-to-noise ratio (SNR) obtained at a high level, compared with the slope of the same function obtained at low level.

Discussion

Signal Detection Theory based Approach

The intensity coding of a stimulus is carried out through the joint intervention of several groups of fibers that cover the dynamic range of possible values of the stimulus. A system of this type is called a multiple channel sensory system. It is characterized by having a number of receivers working in parallel, covering different stimulus ranges, thus achieving a greater dynamic range, with better characteristics of linearity and resolution than if a single group of receivers were used. A single receiver cannot encode all possible values of a stimulus because the firing rate (the frequency of the action potentials it can generate) is limited. For this reason, it is not possible to achieve linearity, high dynamic range and high sensory discrimination at the same time. In sensory systems this problem is solved by a strategy consisting of different groups of neurons starting to respond from a certain intensity of the stimulus, its respective threshold.

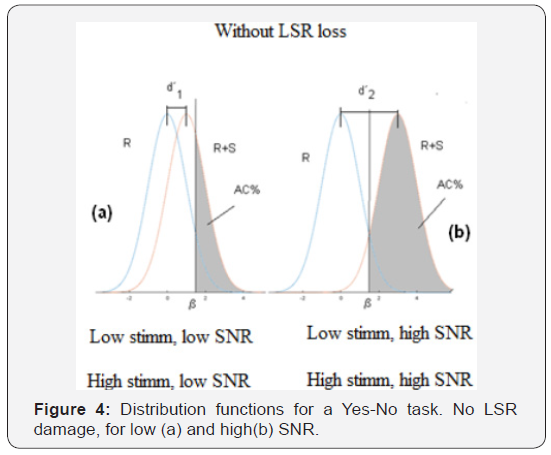
Signal Detection Theory (Green Sweets, 1959) provides an adequate conceptual framework to visualize the different experimental variables that may come into play. In Figure 4a we see the distribution function of Noise (R) and Signal + Noise (S + R), the latter corresponding to a given stimulus, during the course of a Yes-No experiment. On the abscissa axis we represent the internal variable r that reflects the level of sensation, or level of “internal representation” caused by the stimulus. This variable reflects the firing rate of the neurons that are involved in the detection process. The curve on the left shows the probability density of the values of the internal variable, when the stimulus is “noise only”, while the one on the right shows the probability density for the different values of the internal variable, when the stimulus has the signal (the probe tone) added to the noise. In SDT, the variance of both functions is considered to be the same. The decision process of the subject under test consist in comparing the internal variable r the value with a certain value that we call the criterion (β): if this internal variable is higher than the criterion the subject’s response will be YES (signal present) and if it is lower than the criterion, it will answer NO (signal not present). The shaded area, to the right of the criterion, under the curve that shows the combination of signal and noise is the integral of the distribution function that indicates the hit rate (AC) in this type of experiment. The distance between the mean values of both distribution functions is the discriminability d´, also called real sensitivity. Figure 4a shows the case of a presentation in an experiment where the subject detects some stimulus level, above noise level. In other presentation (Figure 4b), with a higher stimulus level, the S + R curve would be moved to the right, thus increasing the area under the curve on the right side of the criterion, and therefore the hit rate (AC). This can be seen as an increase in sensitivity d’(d2’> d1’). The illustrated situation could correspond, for example, to a case of low level stimulation or also to the case of high signal and noise levels. The decision process in both cases is similar, but the stimulus levels and the values of the internal variable are modified. Now suppose a situation where the stimulus and the noise are of high level, but where the subject tested suffers the loss of synapses in the fibers of low spontaneous rate. This should be reflected in the previous curves as a shift of the Signal + Noise distribution function to the left. For the same stimulus values as in the previous case (equal signal to noise ratio), the decrease in the number of synapses with a low spontaneous rate results in lower values of the internal variable r. Then we could have the situation showed in Figure 5. Although the criterion has not been modified, the smaller distance between the distribution function curves (d’3 < d’2), that is, the lower sensitivity will be reflected in a smaller number of hits. The shaded area has decreased. The difference between the shaded areas is directly related to the difference in the hit rate and the percentage of detections, which is the value represented on the ordinate axis in the psychometric function (Figure 5a).

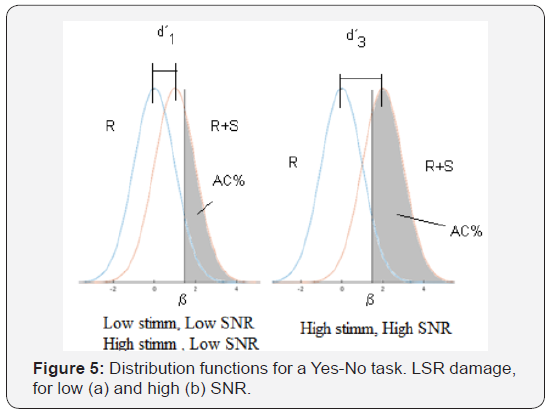
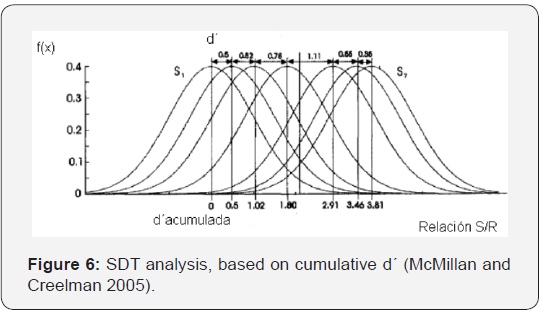
For a higher stimulus, compared with noise (in other words, a higher signal-to-noise ratio), the same thing will happen: there will be a difference between the distribution functions with and without the disfunction of LSR fibers. And there will be a difference in the distribution functions in low and high level of stimulation, which should be more evident in that at high levels there is a greater degradation of the synapses. The difference between the shaded areas of (Figures 4b & 5b) indicates that we can expect a decrease in the slope of the psychometric curve, in cases where there is actually a decrease in the number of synapses. Another way to understand this is to consider the graph that shows the cumulative sensitivity obtained for different stimulus values. Based on an analysis similar to that of McMillan and Creelman (2005), it is possible to evaluate the cumulative sensitivity (d’ac) related the stimulus value. This graph shows the spacing in the aspects of the sensory and physical stimulus and its slope tells us how fast the perceptual effect increases with the variation of the stimulus. Figure 6 represents the different distribution functions that correspond to different stimulus values and their corresponding sensitivity values (d’). The cumulative sensitivity is shown in horizontal axis.

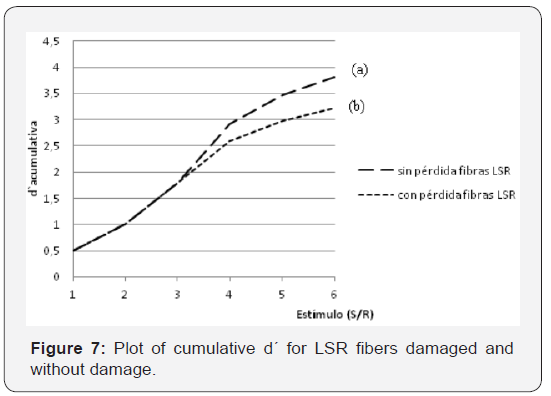
In Figure 7 shows curves of cumulative sensitivity as a function of the stimulus level (SNR). The figure shows two curves, curve (a) corresponds to a subject that does not have LSR loss. In curve (b) the argument derived by [3] is used, which calculated that, as a maximum, the decrease in sensitivity at the threshold level due to a loss of synapses of 50% would be in the order of √ 2 , that is, 1.5 dB. By affecting the sensitivity values for this same factor and finding the cumulative sensitivity we obtain a representative curve of the case of absence of 50% of LSR fibers. Looking again at Figure 6, it is evident that, for equal values of SNR, the distribution functions will tend to be closer to the one belonging to noise only. This can be understood as a horizontal compression of the distribution functions in the Figure 7. It should be noted that, as the stimulus grows, it is necessary the cooperation of a greater population of fibers of low spontaneous rate to achieve detection. If these are absent due to a synaptopathy, higher stimulus values will be necessary in order to obtain a higher success rate, which is translated in a lower slope in the psychometric function. The conjecture we present considers that the slope of the psychometric curve of SNR ratio at high levels of stimulus must be lower than the slope of the same curve at low levels, when the subject suffers some type of disorder in the fibers of high threshold and low spontaneous rate.

Approach through a Mathematical Model

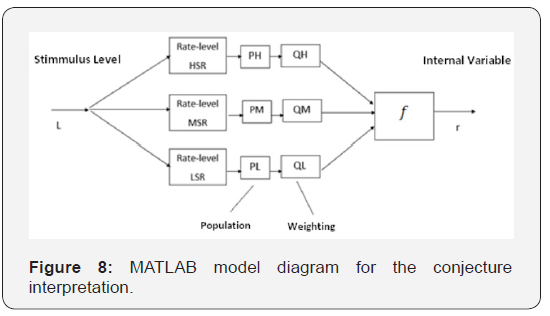
A simplified model was developed in MATLAB to conceptually visualize and estimate the practical scope of the conjecture. It represents a population of fibers with different spontaneous firing rates and thresholds, characterized by the Rate-Level curves. Many authors [19,20] have published curves resulting from measurement under different conditions. The aim of this model is to represent the effects of the variables that define the function that relates the stimulus level (L) and the internal variable (r). A block diagram of the model can be seen in Figure 8. Each of the Rate-level blocks contains the average transfer function (Spike rate vs. stimulus level) of the average neurons for each of the types identified by [20], that is, high, medium and low spontaneous rate (HSR, MSR and LSR, respectively). These functions provide information on the spontaneous firing rates, the thresholds and the dynamic ranges of each of these types of receivers. Blocks PH, PM and PL take into account the populations of the different types mentioned, while the Q coefficients account for other weighting factors that affect the conformation of the internal variable. These weighting factors act together with the last block (f) which is responsible for translating the combination of the individual stimuli into the internal variable. Different combination rules that would imply different expressions for the function f have been suggested. A simple additive model is assumed for the formation of the internal variable r. Of course, this is not the only possible model, but it is the most simple and appropriate to the scope of this work, because only a qualitative justification is sought. The rate - level functions proposed in the work published by [21], adequately represent the characteristics observed in the direct measurement works consulted (Winter, Robertson and Yates (1989) in guinea pigs, and Hellstrom and Schmiedt (1990) in gerbils and [20] in cats. Colburn et al present several possible mathematical expressions, but the one that best reflects the aspects that we want to take into account in our analysis is presented by functions defined by sections.

For the different groups of neurons, the firing rate depending on the level is given by:

High Spontaneous Rate Neurons (HSR):

Medium Spontaneous Rate (MSR):

Low Spontaneous Rate (LSR):

The values assumed in this model are:

a) Spontaneous Rates:

Low threshold: S_RH=50 spikes/seg

Median threshold: S_RM=10 spikes/seg

High threshold: S_RL=0,5 spikes/seg

b) Saturation Levels:

Low threshold: LH_SAT=45 dBSPL

Median threshold: LM_SAT=60 dBSPL

High threshold: LH_SAT=80 dBSPL

In the same work, (Colburn et al. op. cited) a plot that clarifies the influence of the different fiber groups on the sensitivity index (squared) is shown in Figure 9. It can be seen, once again, how the LSR fibers (Low, in the graphic) contribute a much more important proportion in high levels, with respect to those of medium and high spontaneous rate to this index. Considering the functions described in the previous paragraph, the average rate-level curves for each type of fibers are shown in Figure 10.

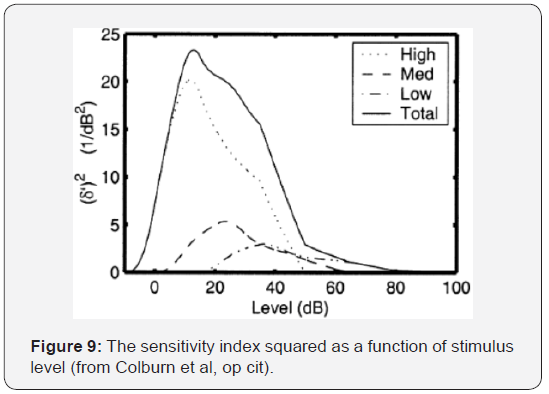
The population of each type (high, medium and low spontaneous rate) is not homogeneous. According to [20] the proportions of high, medium and low spontaneous rate are, 60%, 25% and 15% respectively. Once we have the average rate-level for each type of fiber it is necessary to combine the information from the different sensors to generate the value of the internal variable of sensation (r, in the SDT). This is the classic problem of encoding the level of a stimulus, based on the knowledge of the response to the stimulus of a set of neurons. The work of Colburn, Carney and Heinz (op. cit) provides an adequate theoretical framework for this analysis. A useful parameter to relate the performance in psychoacoustic experiments of stimulus detection with the theoretical predictions based on the behavior of the individual receptors is the measure of the sensitivity per decibel δ ‘ [21], defined as:

Where L and L + ΔL are the stimulus levels measured in dB and d´ is the sensitivity as defined in SDT, that is, the distance between the mean values of the distributions of both stimuli, expressed in units of standard deviation. Colburn et al, 2000 suggested three combination rules:

c) Optimal Combination (Siebert, 1965, 1968)

d) Single Channel at a Time (Zwicker, 1956)

e) Total Count (Goldstein, 1974)

Assuming optimal combination rule: (Siebert):

As d´is calculated as:

This means that:

Thus we can write the internal variable r as follows:

r (L) is expressed in units of the internal variable, K is an scale factor and km is a weighting factor that takes into account populations of different fiber groups. Combination rules provide different ways to find the magnitude of the internal variable of sensation. In a first analysis we used the simplest one based on the linear combination of the responses of the different groups of cells, weighted according to their population (PL, PM and PH factors) and their degree of survival (factors QL, QM and QH). This corresponds to the sum of the contributions of the different fiber groups.

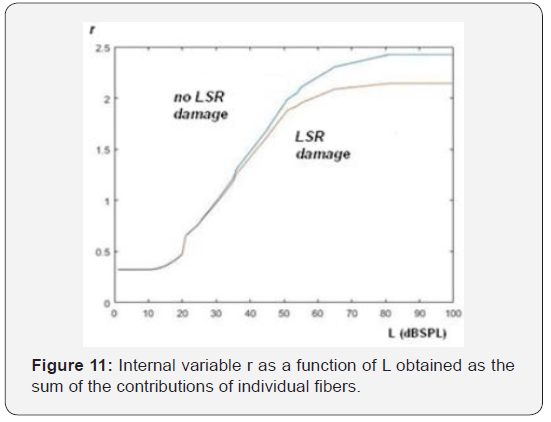
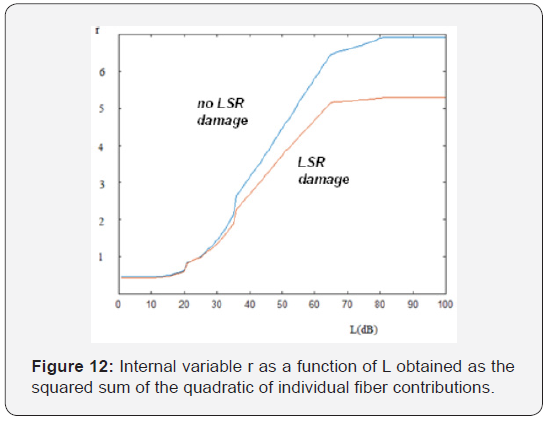
The upper curve in Figure 11 shows the result of the application of the model, to the case of not damaged fibers in the three groups of receptors, Instead, the lower curve, consider a decrease in the number of high threshold receptors of 50% and a decrease in the receptors of medium threshold of 20%, [23- 35] keeping intact those of low threshold. Note that the slope corresponding to the case of absence of high threshold receptors is lower than in the case of intact receptors. If we apply the model suggested by Siebert and calculate the internal variable through the square root of the sum of the squares of the firing rates of the individual fibers, we obtain the result shown in Figure 12. We can also note here the slope difference between the curves at high level, in the case of dysfunction in LSR fibers.

Conclusion

a) The association between the psychometric function for Yes-No experiments and the rate-level curve for fibers of the auditory nerve has been proposed by different authors. This allows suspecting that the loss of some synapses may have some visible manifestation in above function.

b) Both the reasoning based on the Signal Detection Theory and the prediction based on a simplified model of the diverse groups of the auditory nerve fibers behavior allow to raise the conjecture that the effects of the auditory synaptopathy should be detectable through the comparison of the slopes of psychometric functions for high and low levels of stimulation.

c) The model predicts a decrease in the slope of the FP for high levels stimmulation in cases where there is no loss of LSR fibers but predicts a greater decrease in cases where there is such loss.

d) This observation should be verified experimentally through tests that seek to correlate results with other indicators of supposed auditory synaptopathy.

e) Starting research along this path, a set of psychophysical experiments was designed for the detection of absolute thresholds and the survey of psychometric functions. It is in trial stages and is part of a larger work that consists in the evaluation and analysis of correlation of different indicators of the presence of a possible synaptopathy.

GJO.MS.ID.555969

Our Media Partner

GJO Menu

Useful Links

Downloads