Abstract

This paper looks into the parametric study of the deflection of double-walled Carbon Nanotubes. Using the Bernoulli-Euler beam theory, a beam model is developed for the transverse displacement of double-walled carbon nanotube under compressive axial load. The model includes the effect of the axial load and also the effect of the van der Waals force that exists between the inner and outer tubes of the carbon nanotube. Expressions for the deflection of the carbon nanotube, a function of both time and space, are derived and solutions are obtained by applying Galerkin’s decomposition method (which allows focus on the temporal aspect of the deflection) and Differential Transformation Method (DTM). The solutions are treated using the Cosine After Treatment (CAT) technique to produce converging equations. Graphs of the dynamic response analysis (deflection against time) and steady-state analysis (deflection at certain points on the beam length) and observations are made. The graphs generally describe how the deflection is affected by both temporal and flexural aspects, since it is dependent on both time and space. It is seen from the dynamic response that the inner tube vibrates more than the outer tube does. Also, the number of deflections present along the length of the double-walled carbon nanotube increases as the mode number increases.

Keywords: Dynamic Response; Steady State; Double-Walled Carbon Nanotube; Compressive Axial Load; Galerkin Decomposition Method; Differential Transform Method; Cosine After Treatment.

Nomenclature:F: Compressive Axial Load; V: Shear Force;M: Moment of force; ω: transverse deflection of the tube; x: axial length; A: Cross-sectional Area; ρ: mass density; m: mass; a: acceleration;E: Young’s Modulus; I: Second moment of Area; t: time; 12P: Van der Waals pressure; c:innertube interaction coefficient; 0xσ: axial stress; 0()ea: Non-local parameter; Ω: Initial static displacement; L: Length of the tube.

Introduction

Carbon Nanotubes were discovered by Iijima in [1], and since then have generated lots of huge activities in most areas of science and engineering due to their unprecedented mechanical, electrical and thermal properties which have led to a lot of resources being put into studies to discover the secrets of these innovative materials. Treacy et al. measured the amplitude of intrinsic thermal vibrations observed in Transmission Electron Microscopy (TEM) and the average value of Young’s modulus of Carbon Nanotubes derived from this experimental technique was 1.8 TPa [1]. Poncharal et al. obtained Young’s modulus of CNTs which is between 0.7 and 1.3 TPa by electromechanical resonant vibrations [1]. Based on an atomic force microscope (AFM), Wong et al. in 1997 firstly directly measured the stiffness constant of armchair Multi-walled Carbon Nanotubes pinned at one end, from which the value of Young’s modulus of Carbon Nanotubes is 1.28 TPa [1]. Salvetat et al. used the AFM for experiment of bending an armchair Multi-walled Carbon Nanotube pinned at each end over a hole and obtained an average modulus value of Carbon Nanotubes of 0.81 TPa [1]. In 1993, Overney et al. calculated Young’s modulus of rigid short Single-walled Carbon Nanotubes which is 1.5 TPa, approximately equal to that of graphite [1]. Lu who also used the MD approach, reported that Young’s modulus is 1 TPa and claimed that chirality and the number of walls have little effect on the value of Young’s modulus [1]. Yao and Lordi made use of a different potential model and obtained Young’s modulus of CNTs as 1 TPa [1].

P. Soltani et al.[2] performed a periodic solution for nonlinear vibration of a fluid conveying single-walled Carbon Nanotube showing that the deviation of the nonlinear flow-induced frequency from the linear frequency is considerable when the amplitude, flow velocity and non-local parameter are high while for the CNTs embedded in the mediums of high Pasternak parameters, the nonlinearity of the model does show any effect on the frequency. M. Hosseini et al. [3] performed research on the vibration analysis of single-walled Carbon Nanotube conveying fluid while being subjected to a longitudinal magnetic field with results showing that in the presence of a strong longitudinal magnetic field, the influence of internal fluid flow and nonlocal parameter on the vibrational frequencies of the single-walled CNT can be reduced.

M. Malikan et al. [4] carried out an analysis of damped forced vibration of single-walled carbon nanotubes resting on a viscoelastic foundation in a thermal environment and showed that the higher the value of the nonlocal parameter, the more the effects of abating resonant vibration would be increased in the physical structures of the nanotube. R. Ansari et al. [5] carried out a study on the Torsional vibrational analysis of Carbon Nanotubes based on the Strain gradient theory and Molecular Dynamic simulations and were able to notice that the size effect had a significant role in the vibrational response of nanotubes in small aspect ratios. S. Takahashi et al. [6] performed analysis of flow induced vibrations in closed side branch pipes showing that adding another side branch with an orifice was very effective in suppressing the flow-induced acoustic resonance. M. Malikan et al. [7] performed a buckling analysis of a non-concentric double-walled carbon nanotube and concluded from their results that being off-center in the double-walled CNTs reduces the effects of the inner tube’s boundary condition.

X. Yi et al. [8] performed a vibrational analysis of fluid conveying carbon nanotubes based on Nonlocal Timoshenko Beam Theory by Spectral Element method, they were able to conclude that the effect of internal fluid velocity on the natural frequencies of the Single-walled CNT conveying fluid is the same as that of a macro pipe conveying fluid. H. Aminikhah et al. [9] carried out research work on the nonlinear vibrations of Multi-walled Carbon Nanotubes under various boundary conditions applying the Homotopy Perturbation method. Their results showed that the nonlinear vibration frequency of the nanotubes rose quite rapidly with an increase in the amplitude. D. M. Santee et al. [10] performed a research work on the oscillations of a beam on a nonlinear elastic foundation under periodic loads using analytical and semianalytical perturbation methods to carry out a parametric study. M. Shaban et al. [11] worked on free vibration analysis of carbon nanotubes by using three-dimensional theory of elasticity. S. Zghal et al. [12] did a research work on free vibration analysis of carbon reinforced functionally graded composite shell structures and they did a comparison study of the vibrational behaviour of the various functionally graded composite shell structures. C. Dinckal [13] carried out work on free vibrational analysis of Carbon Nanotubes by using finite element method making use of both the Bernoulli- Euler and Timoshenko beam theories.

S. Oveissi et al. [14] performed longitudinal vibration and stability analysis of carbon nanotubes conveying viscous fluid showing that there is a decrease in the natural frequencies of the system caused by the fluid flowing in the nanotube. S. Kamarian et al. [15] worked on free vibration analysis of conical shells reinforced with agglomerated carbon nanotubes. M. Aydogdu [16] carried out work on axial vibration analysis of carbon nanotubes embedded in an elastic medium using non local elasticity, hence showing that the axial frequencies of the embedded nanotubes are highly overestimated by the classical continuum rod model. C. D. Reddy et al. [17] performed research on free vibration analysis of fluid-conveying single-walled carbon nanotubes. They were able to develop an expression which was used to measure the mass flow rate of the fluid velocities. T. Natsuki [18] engaged in a research work on vibrational analysis of embedded carbon nanotubes using wave propagation approach. S. Asghar et al. [19] carried out the research on non-local effect on the vibration analysis of doublewalled carbon nanotubes based on Donnell shell theory which showed the possibility of performing free frequency analysis of DWCNTs using the developed non-local elastic shell model. S.K. Georgantzinos et al. [20] worked on making an efficient numerical model for vibration analysis of single-walled carbon nanotubes giving new natural frequencies and mode shapes for different support conditions. C. M. Wang et al. [21] did a research work on using Timoshenko beam model for analysis of multi-walled carbon nanotubes.

Model Formulation

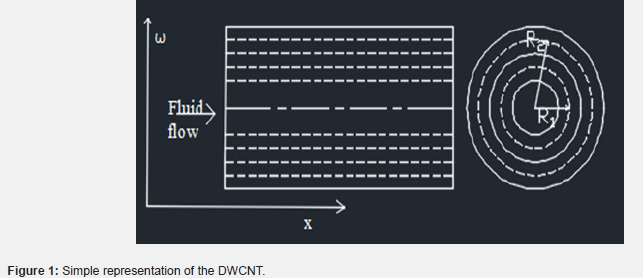
The Double Elastic beam model: (Figure 1)

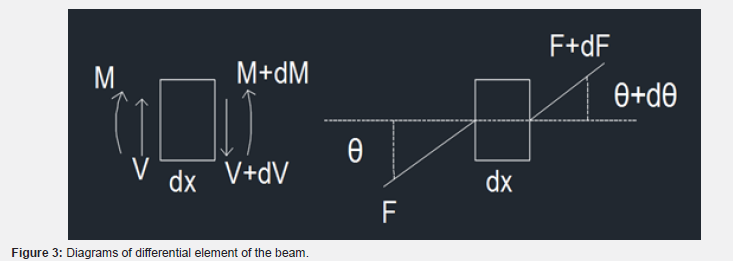
By following the Bernoulli-Euler beam theory [22] , the general equation for transverse vibrations of an elastic beam under compressive axial load can be obtained (Figures 2 & 3):

Consider a small slice of the beam as shown above,

Which can be rearranged to give,

Also, since ω is a function of both the axial coordinate, x , and the time, t, hence.

However, for double-walled Carbon Nanotubes, it is known that the presence of the innertube Van der Waals forces is one major distinguishing factor from traditional single-walled nanotubes. Assuming that both inner and outer tubes possess the same material constants [23-25], Eq. then becomes

where the subscripts 1 and 2 are used to indicate the quantities associated with the inner and outer tubes respectively, and P12 represents the Van der Waals pressure per unit axial length exerted on the inner tube by the outer tube.

By considering the Lennard-Jones model, the Van der Waals pressure at any point between the two tubes is given as a linear function of the jump in deflection at that point, which is expressed as

Where c is the innertube interaction coefficient per unit length, which is estimated by,

Where R₁ is the radius of the inner tube and d = 0.142nm. Thus, the equation of the model can then be written as:

These two equations describe the free transverse vibrations of double-walled carbon nanotubes under compressive axial load.

Analytical Solution to Model

Non-dimensionalizing the equations

The Non-dimensionalized forms of the equations are:

Non-local theory

In order to fully represent the model as a nanostructure and set it apart from the macrotubes (larger, normal sized tubes), the Eringen’s non-local theory is used. Eq. (11) and (12) then become.

And with further simplifying.

Galerkin’s decomposition Method

Applying Galerkin’s decomposition method, in which ω(x,t) =ε (t).φ (x) to Eq. (15) and (16), taking the Eq. (15) first, Term 1 becomes:

Solution of the model using Differential Transformation Method (DTM):

Applying Cosine After Treatment (CAT) technique

The Cosine After Treatment (CAT) technique is then introduced and applied to Eq. (43) and (44). This is done in order to produce new equations whose results would converge and enable proper analysis to be carried out [26-29]. The equations are.

Hence, the deflection of the carbon nanotube, ω , becomes,

For the outer tube.
Where φ (x) is the boundary condition.
For simply supported boundary condition,

Results and Discussion

Dynamic Response Analysis

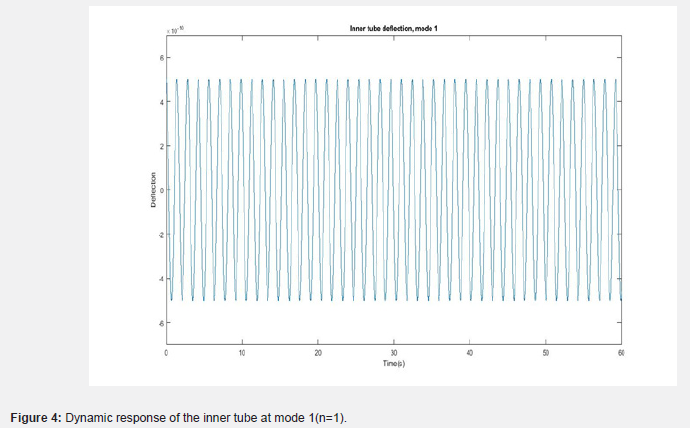
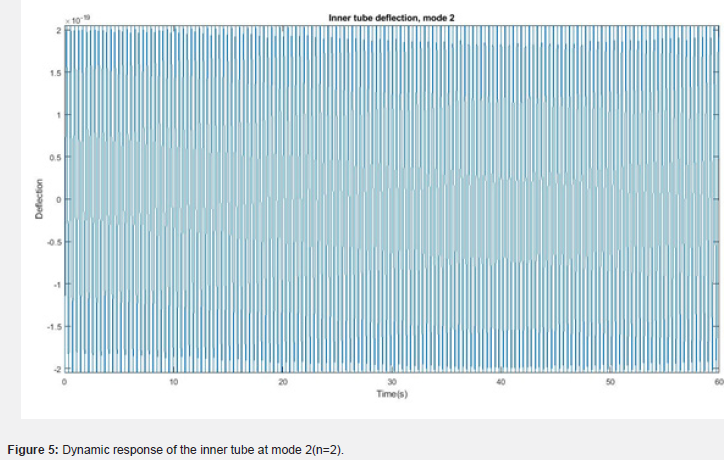
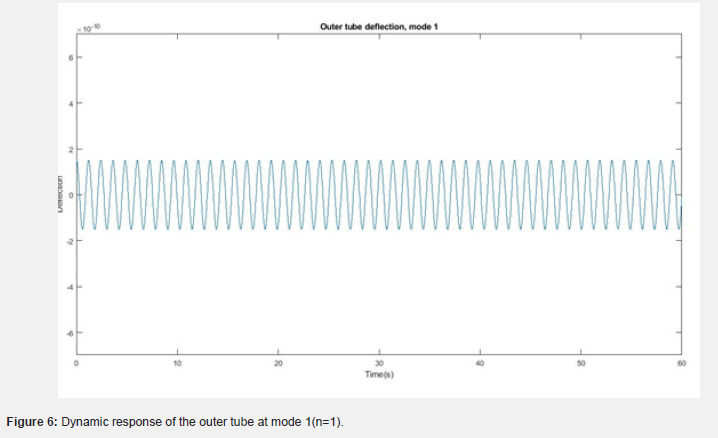
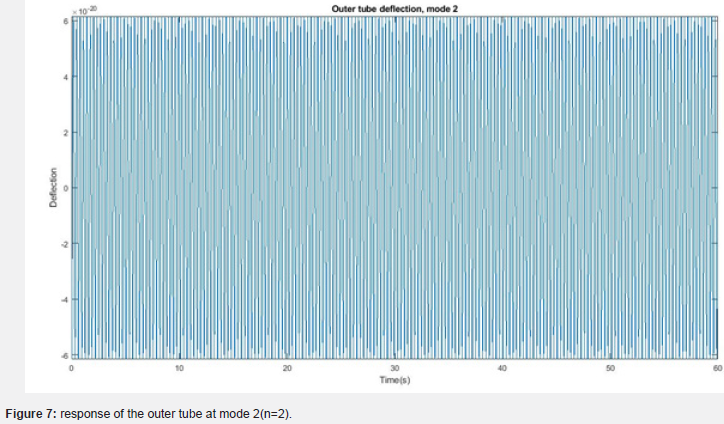
(Figures 4-7) show graphs representing the dynamic response of the double-walled carbon nanotube at different mode values. (Figure 4) shows how the deflection of the inner tube, at mode 1 varies with time. (Figure 5) shows the deflection of the inner tube at mode 2. (Figure 6) shows that of the outer tube at mode 1 while (Figure 7) is that of the outer tube at mode 2. The plots show that there is a significant increase in frequency of the vibration of the tubes as the mode number is increased, though the amplitude decreases [30].

Steady-state Analysis

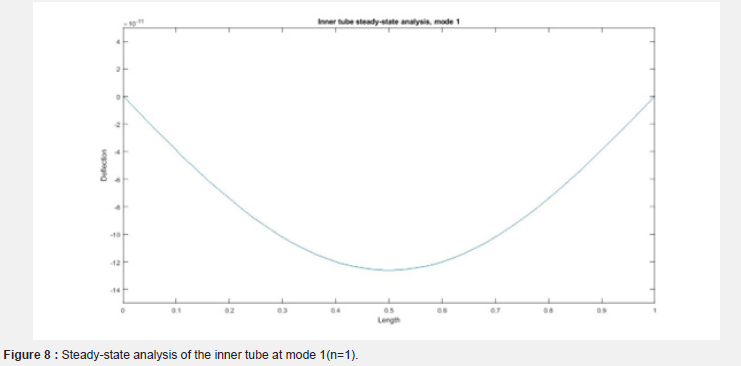
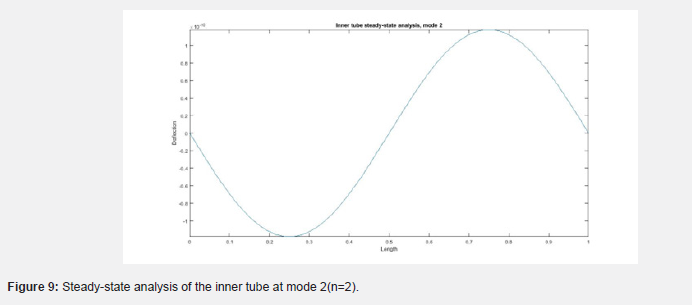
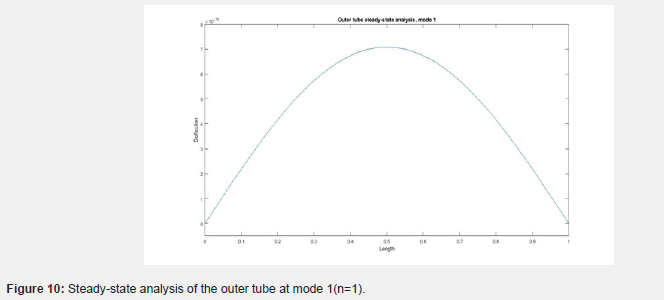
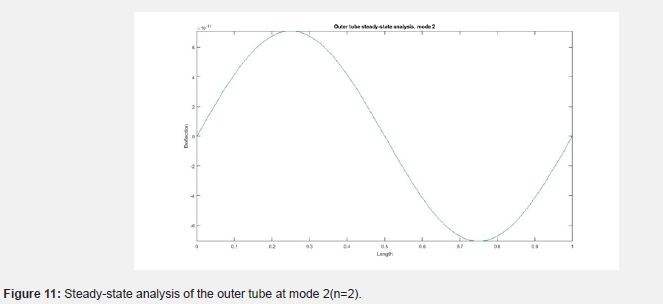
(Figures 8-11) show the deflection of the double-walled carbon nanotube along the length of the tube. (Figure 8) shows the deflection of the inner tube plotted against points on the length of the nanotube. (Figure 9) shows that of the inner tube at mode 2. (Figure 10) shows the deflection of the outer tube along the length of the tube at mode 1 while (Figure 11) shows that for mode 2. The plots show that as the mode number increases, the number of deflections along the length also increases [31-33].

Conclusion

Based on the results and graphs obtained and displayed, it is therefore concluded that the modal number is a factor which greatly affects the dynamic response of the double-walled carbon nanotube, seeing as the amplitude of mode 2 is much smaller than those of mode 1. This means simply changing the modal number will cause such a large change in the vibration motion of the double-walled carbon nanotube. This is true for both the inner tube and outer tube. The inner tube also vibrates more than the outer tube.

Also looking at the steady-state analysis, the inner and outer tubes responded to it and behaved quite differently from one another. An increase in the modal number had a notable effect, adding an extra deflection of the tube. Another difference in behaviour is seen between the inner and outer tubes, with the inner tube displaying deflection in opposite direction to that of the outer tube. This is important to note that different measures or a combination of measures could be required to handle and control it.

Some other analyses can be carried out such as the stability analysis for instance. Having many more analyses results would help to give a better picture of the behaviour of the double-walled CNT. Also, analysis should be done for many other boundary conditions for the double-walled CNT in future works. This would help with the observation of the behaviour under the different conditions and can also serve as a comparison to select the most favourable condition under which the double-walled CNT should operate.

In summary, the students have the opinion that the technical assistance has been enhanced, and they acknowledge the advantages of the newly implemented learning culture. According to the results of our investigation, digitalization is connected to modernist and reflective learning settings. The use of digital technology in education is generally seen as a progressive and open-minded movement. In addition, most respondents had a positive opinion of the institution. On the other hand, the frameworks for digital services have room for improvement. The idea still needs to be clarified to everyone involved. In addition, the staff members could be able to commence the process of digitalizing the services and the instruction.

Discussion

Following the data analysis, we will discuss the students’ first suggestions for future improvement. Each of the proposed solutions is adapted to meet the needs of a particular stakeholder group, such as the institution’s management, the administration, the lecturers, and the students. The management of the institution plays an essential role in the process of formulating a digitalization strategy. It is essential to have institutional support, to be innovative, and to be open to change (Reid, 2014). The organization’s leadership should significantly promote digitalization-related initiatives and academic programs. Students have demanded that the university create guidelines for the use of digital media in classroom instruction and that educators be incentivized to adapt their pedagogical practices in response to this demand. As a kind of aid, universities must provide financial funding to develop new prospects for digital workers. Many students believe that the digitization of academic services and instruction is necessary for the continued and accelerated development of efficient learning management systems at the administrative level. The capacity to interact with the content, the provision of chat-based forums, the availability of all content without the need for a continuous internet connection, and compatibility with any and all end devices were the aspects that were emphasized. Students would also want to see an increase in the number of computer labs available to them so that they do not need to bring their own electronic devices.

It is essential to make the most of all the possibilities that technology provides, and not simply the availability of online services. It is essential to find a way to get over the lack of support from institutions (Porter & Graham, 2016). Students maintain that their professors need to live up to their full potential at this time. In order for educational institutions to be successful in overcoming these challenges, they will need to build service centers that help instructors in the process of digitizing courses and transforming them into blended learning environments. Learners and instructors should have easy access to personnel with adequate technical support training. As a direct consequence of this, educators are given the freedom to concentrate on the subject matter rather than the medium. In the long term, a fruitful exchange will result in well-trained staff who clearly emphasize media competence and content production, which will increase the media richness at institutions. The findings of the current study indicate that there is a greater propensity among lecturers to make the transition to digitalized versions of their classes and seminars. However, digitalization calls for a substantial extra amount of work, which can be beyond the lecturers’ capabilities in terms of their time and expertise. Even if professors are willing to investigate more digitalized methods of teaching, their hesitation in doing so may be caused, at least in part, by a lack of knowledge as well as a great deal of uncertainty over how to incorporate digital media into classes appropriately. As a direct consequence of this, pupils have the misconception that resource bundling is obligatory. It is important to connect the digital architecture of individual departments and the whole institution. The outcomes of this research suggest that educators are more inclined to make the switch to digitally delivered classes and seminars. Digitization, however, requires a significant extra effort that may go beyond the lecturers’ capabilities regarding their time and knowledge. Even if professors are open to experimenting with more digitalized modes of education, their reluctance to do so may be due to a lack of knowledge and uncertainty over how to incorporate digital media into classes correctly. Because of this, pupils believe that resource bundling is essential. Connecting digital structures on a departmental or even a university level is something that has to be done. With the assistance of the service locations that were previously outlined, storage facilities may be dismantled.

Conclusion

The generalization of domestic research that has been dedicated to the topic of the digitalization of higher education enables us to conclude about the generality and importance of the problem, both from the viewpoint of the application of technologies and their scientific and theoretical conceptualization, i.e., a suitable mix of classroom, customized, and remote learning, the use of digital technologies in line with the objective of the lesson, etc. Some additional insights that this study revealed about the digitalized LMS system surprised the researchers. They are listed underneath.

The studies on the digitalization of education are relatively varied and typically contain a political element (they describe events surrounding the introduction of digital technologies in education), a regulatory aspect (the study of regulatory legislative acts and legal documents controlling the digitalization process in the nation), a technical and psychological aspect (the teacher’s readiness to be educated to generate and implement digital educational content), and an axiological aspect (the teacher’s willingness to develop and implement digital educational content). In addition, these studies generally have an axiological feature. The integration of digital technology into the teaching process was given a relatively poor rating by students as well as by instructors (3.41 and 3.89, respectively). At the same time, the effect of digitization on scholastic achievement received an above-average rating. Students were observed to assess the teacher’s engagement in the digital world, its usability, and its favorable impact on student motivation differently than did instructors. The degree to which teachers and students concur or dispute the idea that digitalization has improved students’ thinking abilities is another source of debate. As a result, digitalization in higher education frequently represents students’ positive attitudes toward the choices accessible and expectations for future technological advancement. This study undoubtedly gave sufficient detail to improve education and speed up the digitization of higher education, expanding the pool of skilled workers accessible in the digital economy.

References

1. Iijima (1991) A history of Carbon Nanotubes. Azonano.
2. Soltani P, A. Farshidianfar (2012) Periodic solution for nonlinear vibration of a fluid-conveying carbon nanotube, based on the nonlocal continuum theory by energy balance method. Applied Mathematical Modelling 36(8): 3712-3724.
3. Hosseini M, Moslem Sadeghi Goughari (2016) Vibration and instability analysis of nanotubes conveying fluid subjected to a longitudinal magnetic field. Applied Mathematical Modelling 40(4): 2560-2576.
4. Malikan M, Van Bac Nguyen, Francesco Tornabene (2018) Damped forced vibration analysis of sing-walled Carbon nanotubes resting on viscoelastic foundation in thermal environment using nonlocal strain gradient theory. Engineering Science and Technology, an International Journal 21: 778-786.
5. Ansari R, Gholami R, Ajoriet S (2013) Torsional vibration analysis of carbon nanotubes based on the strain gradient theory and molecular Dynamic Simulations. Journal of Vibration and Acoustics 135(5): 051016.
6. Takahashi S, Akinori Tamura, Shunichi Sato, Toshitaka Goto, Michiaki Kurosaki et al. (2016) Flow induced vibrations in closed side branch pipes and their attenuation methods. Journal of Nuclear Science and Technology 53(8): 1164-1177.
7. Mohammad Malikan, Victor Eremeyev A, Hamid Sedighi M et al (2020) Buckling analysis of a non-concentric double-walled carbon nanotube. Acta Mechanica 231: 5007-5020.
8. Yi X, Baohui Li, Zhengzhong Wang (2019) Vibration analysis of fluid conveying carbon nanotubes based on nonlocal Timoshenko beam theory by Spectral Element method. Nanomaterials 9(12): 1780.
9. Aminikhah, Milad Hemmatnezhad (2011) Nonlinear vibrations of multiwalled carbon nanotubes under various boundary conditions. International Journal of Differential Equations 11: p. 1-17.
10. Donald Mark Santee, Paulo Batista Goncalves (2006) Oscillations of a beam on a non-linear elastic foundation under periodic loads. Shock and Vibration 13: 273-284.
11. Alibeigloo A, Shaban M (2013) Free vibration analysis of carbon nanotubes by using three-dimensional theory of elasticity. Acta Mechanica 224: 1415–1427.
12. Zghal S, Frikha A, Dammak F (2018) Free vibration analysis of carbon nanotube-reinforced functionally graded composite shell structures. Applied Mathematical Modelling 53: 132-155.
13. Dinçkal C (2016) Free Vibration Analysis of Carbon Nanotubes by Using Finite Element Method. Iranian. Journal of Science and Technology, Transactions of Mechanical Engineering 40: 43-55.
14. Soheil Oveissi , Davood Toghraie , Seyyed Ali Eftekhari (2016) Longitudinal vibration and stability analysis of carbon nanotubes conveying viscous fluid. Physica E: Low-dimensional systems and nanostructures 83: 275-283.
15. Saeed Kamarian, Mostafa Salim, Rossana Dimitri, Francesco Tornabene (2016) Free vibration analysis of conical sheels reinforced with agglomerated Carbon Nanotubes. International Journal of Mechanical Sciences Volumes 108-109: 157-165.
16. M Aydogdu (2012) Axial vibrational analysis of nanorods (carbon nanotubes) embedded in an elastic medium using nonlocal elasticity. Mechanics Research Communications Volume 43: 34-40.
17. Reddy CD, Lu C, Rajendran S, Liew KM (2007) Free vibration analysis of fluid-conveying single-walled carbon nanotubes. Applied Physics Letters 90: 133122 (2007).
18. Toshiaki Natsuki, Morinobu Endo, Hiroshi Tsuda (2006) Vibration analysis of embedded carbon nanotubes using wave propagation approach. Journal of Applied Physics 99: 034311.
19. Sehar Asghar, Muhammad Nawaz Naeem, Muzamal Hussain (2020) Non-local effect on the vibration analysis of double-walled carbon nanotubes based on Donnell shell theory. Physica E: Low-dimensional Systems and Nanostructures 116: 113726.
20. Georgantzinos SK, Giannopoulos GI, Anifantis NK (2009) An efficient numerical model for vibration analysis of single-walled carbon nanotubes. Computational Mechanics 43: 731-741.
21. Wang CM, Tan VBC, Zhang YY (2006) Timoshenko beam model for vibration analysis of multi-walled carbon nanotubes. Journal of Sound and Vibration 294(4-5): 1060-1072.
22. Yongqiang Zhang, Guirong Liu, Xu Han (2005) Transverse vibrations of double-walled carbon nanotubes under compressive axial load. Physics Letters A 340: 258-266.
23. Xiaowen Lei, Toshiaki Natsuki, Jinxing Shi, Qing-Qing Ni Analysis of Carbon Nanotubes on the Mechanical properties at Atomic scale, Journal of Nanomaterials p.1-10.
24. Orynyak IV, Dubyk YR, Batura AS (2015) Analysis of fluid-induced vibrations of long branched pipelines. Strength of Materials 2(1).
25. Ganesh EN (2013) Single Walled and Multi Walled Carbon Nanotube Structure, Synthesis and Applications. International Journal of Innovative Technology and Exploring Engineering (IJITEE), Volume 2(4): 2278-3075.
26. Timeline of Carbon nanotubes.
27. Carbon Nanotubes, Wikipedia.
28. Physicist Richard Feynman (1959) What It is and How It Works, National Nanotechnology Initiative.
29. Working at the Nanoscale, National Nanotechnology Initiative.
30. Manufacturing at the Nanoscale, National Nanotechnology Initiative.
31. Catharine Paddock (2012) Nanotechnology in Medicine: Huge Potential but what are the risks, Medical News Today.
32. Benefits and Applications, National nanotechnology Initiative.
33. Nanotechnology: A small solution to big problems.