Review Article

Analysis of Single-walled Carbon Nanotube Embedded in Elastic Foundation in a Magneto-thermal Environment Using Differential Transformation Method Coupled with Decomposition and CAT Techniques

A A Yinusa¹*, E H Abubakar² and M G Sobamowo³

^1,3 Mechanical Engineering Department, University of Lagos, Nigeria

² Civil and Environmental Engineering Department, University of Lagos, Nigeria

Submission: April 28, 2023; Published: May 24, 2023

*Corresponding author: A A Yinusa, Mechanical Engineering Department, University of Lagos, Nigeria

How to cite this article: A A Yinusa, E H Abubakar, M G Sobamowo. Analysis of Single-walled Carbon Nanotube Embedded in Elastic Foundation in a Magneto-thermal Environment Using Differential Transformation Method Coupled with Decomposition and CAT Techniques. Eng Technol Open Acc. 2023; 5(2): 555657. DOI: 10.19080/ETOAJ.2023.05.555654

Incorporating

Abstract

The potential use of nanotube has open major chapter in industry and engineering spheres, according to their vast applications in dynamically, buckled and vibrational response of nanotube structure. In our study, the theoretical investigation of SWCNTs is presented. Furthermore, straight Single-walled carbon nanotube is modeled as a pinned-pinned supported beam embedded in both Winkler and Pasternak type’s foundation. For the analysis, nonlocal Euler-Bernoulli beam theory is used to develop the model. The resulting nonlinear equation is solved using the differential transform method after decomposition is used to transform the dimensionless nonlinear partial differential equation (PDE) into ordinary differential equation (ODE) and the solution was treated using Cosine-after treatment (CAT-Technique) to obtain dynamic behaviour of nanotube under four different boundary conditions. Thereafter, parametric studies were carried out to reveal the effects of the magnetic term, thermal term, Winkler and Pasternak types elastic foundation and mass, on the vibrational and stability analysis of the SWCNTs structure.

Keywords: Carbon Nanotube; Magnetic; Thermal; Differential Transform Method; Elastic Foundation

Introduction

The potential use of Nanotube has open major chapter in industry and engineering spheres, according to their vast applications in dynamically, buckled and vibrational response of nanotube structure is a challenging and considering their important in tomorrow’s society. Therefore, their vibration investigation is examined for successful usage. Payam et al. [1] studied usage and application of carbon nanotube in various fields. However, they use Bernoulli-Euler’s (EB) model to explore vibrational response of CNTs under magneto-thermal environment resting on both elastic foundation models. They considered effects of various controlling parameters in the model. More so, the following beam ends conditions such as fixed-fixed, simply supported, fixed-simple ends conditions have been employed to analyzed the vibration of natural frequencies. Natsuki et al. [2] analyzed different lengths of inner and outer double-walled carbon nanotubes (DWCNTs) using theoretical approach. The analysis will be useful dynamically response and others.

Ghasemi & Gouran [3] assessed vibrational and frequency analysis of (SWCNTs) conveying fluid flow resting on Pasternak foundation. Thereafter DTM and VIM was employed to solve the nonlinear equation in order to validate other method used. Subsequently, parametric analysis revealed of the following, flow velocity, amplitude, nonlocal parameter and axial tensions on variational SWCNT’s frequency. The outcomes indicate that increment of the nonlocal parameter leads to enhancement in variation of frequency. Conclusively, the frequency variation of the SWCNT increases with the corresponding of the parameters. Tyagi et al. (2021) investigated analytical free forced vibration of SWCNTs elastic foundation subjected to different parametric studies. Therefore, Krylov–Bogoliubov-Mitropolsky (KBM) method was used to solve theoretical nonlinear equation. Alibeigloo & Jafarian [4] considered shell three-dimensional theory of elasticity and analytical solution of Fourier series alongside the axial and radial coordinates for the pinned-pinned supports. Valipour et al. [5] studied nonlinear vibrational analysis of SWCNTs resting on elastic spring. Therefore, they use homotopy perturbation method was used to analyzed the model equation. Thereafter, effects of the parametric investigation show the parameters considered were all in agreement. Mohammadimehr & Alimirzaei [6] used Euler-Bernoulli theory to investigate composite beam model reinforced by functionally graded SWCNTs with initial geometric imperfection use (FEM).

Farshidianfar & Soltani [7] investigated immovable simply supported SWCNTs conveying fluid not perfectly straight resting on elastic spring. Principle of perturbation was employed to solve the flow-induced duffing equation. Soltani et al. [8] analyzed pinned-pinned supports SWCNTs using von Karman’s geometric nonlinearity and nonlocal shell theory. Galerkin’s procedure was used to discretized partial model equation into an ordinary differential equation and the method of averaging was employed to obtained nonlinear vibration of (10,0), (20,0), and (30,0) zigzag SWCNTs. Mu’tasim et al. [9] used nonlocal elasticity theory on vibrational analysis of SWCNTs were assumed to have an imperfection modeled as half sine and fixed at both ends. The principle of both Euler-Bernoulli Beam and Hamilton’s principle were applied to solve nonlinear equation. Mahmoud [10] investigated SWCNTs with surface irregularity and compressive initial stresses. Thereafter, model governing equation of closedform solutions was derived. Numerical results were discussed and presented graphically. Yu-Chi & Tse-Yu [11] studied SWCNTs embedded in an elastic spring using nonlocal Timoshenko beam model, slenderness ratios, boundary conditions, atomic structures and the stiffness of the embedded medium on the natural frequencies and mode shapes. Fatahi-Vajari & Azimzadeh [12] used Homotopy perturbation method (HPM) to solve partial differential equation of motion. The influences of some commonly used boundary condition were analyzed and discussed extensively. Murmu & Pradhan [13] investigated SWCNTs stability response embedded in two foundation types and the model equation was solved differential quadrature approach. Hassen & Mohammad [14] estimated accurately the natural frequencies of electrically actuated carbon nanotubes (CNTs) as robust knowledge is still missing in the understanding of the role of various physical parameters affecting the natural frequencies. Farshidianfar & Soltani [7] investigated flow induced singlewalled carbon nanotube on with immovable support conditions is assumed not perfectly straight with initially including a slight geometrical curvature as an imperfection using the perturbation method of multi scales (MMS). Ghorbanpour & Zarei [15] presented Homotopy analysis method (HAM) to analysis flow induced Y-shaped SWCNTs using Euler Bernoulli beam theory and von Karman geometric nonlinearity on the vibrational analysis of beam model subjected to magneto-thermal environment with Lorentz force in transverse direction. A scrutiny of previous studies elaborated that small amount of works have been reported on the theoretical analysis of Single-walled Carbon Nanotube. Hence, this present study presents a theoretical study of Single-walled Carbon Nanotube Embedded in nonlinear elastic Foundation in a Magneto-thermal Environment using Differential Transformation Method (DTM).

Model Formulation

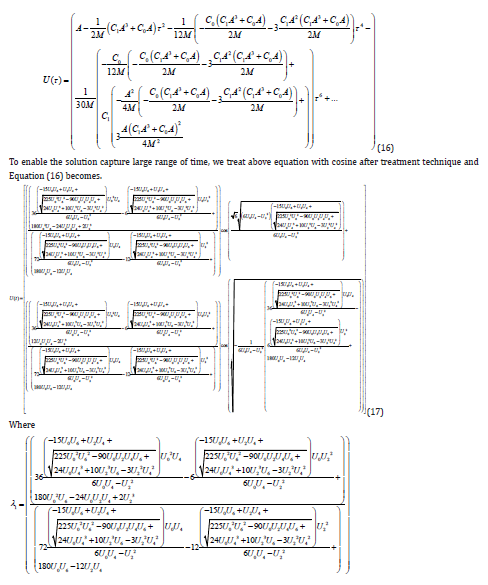
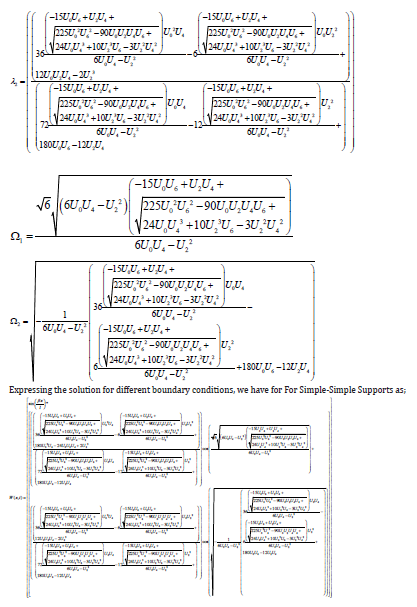
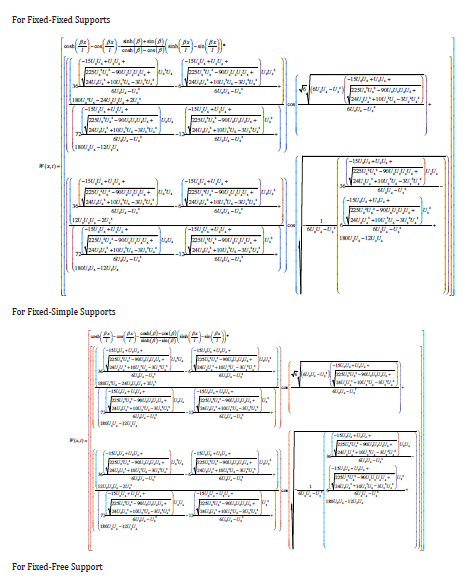
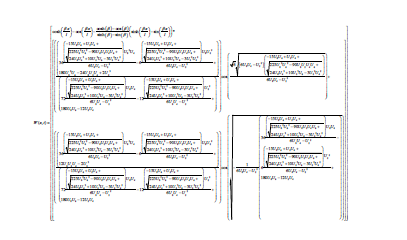
Analytical Solution to Model Formulation

a. Brief And General Understanding Of DTM

The concept of this method was first proposed and applied to solve linear and non-linear initial value problems in electric circuit analysis. It can therefore be applied to solve the transient ODE developed in this present study (Table 1).

Using the Nondimensional parameters below.

Results and Discussion

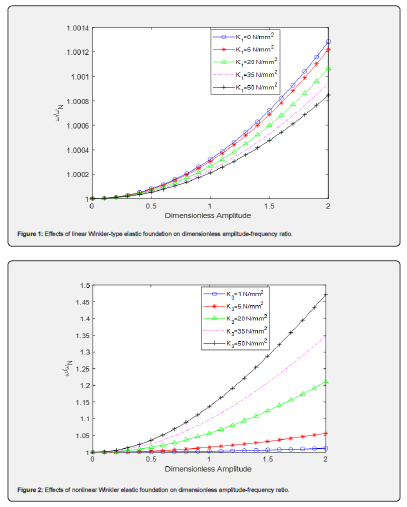
(Figures 1-10) The above (Figure 1), shown impacts of the linear elastic foundation on dimensionless amplitude-frequency ratio curve of stability of single-walled carbon nanotube structure in magneto-thermal environment under two elastic foundations. The curve depicted that as linear Winkler-type elastic foundation increases from zero to maximum, frequency-ratio decreases toward linear system. This shows that for SWCNTs structure gain stability, linear Winkler-type elastic foundation must be kept at maximum.

The above (Figure 2), shown impacts of the nonlinear elastic foundation on dimensionless amplitude-frequency ratio curve of stability of single-walled carbon nanotube structure in magnetothermal environment under two elastic foundations. The curve depicted that as nonlinear Winkler-type elastic foundation increases from zero to maximum frequency-ratio increases above linearity system. This shows that for SWCNTs structure gain stability, nonlinear Winkler-type elastic foundation must be kept at minimum value as control measure of the single-walled nanotube structure.

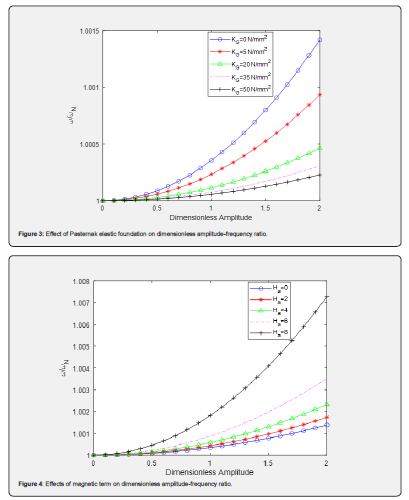
The above (Figure 3), shown impacts of the Pasternak-type elastic foundation on dimensionless amplitude-frequency ratio curve structure in magneto-thermal environment under two elastic foundations. The curve depicted that as Pasternak-type elastic foundation increases from zero to maximum, frequencyratio decreases toward linear system. This shows that for SWCNTs structure gain stability, Pasternak-type elastic foundation must be kept at maximum.

The above (Figure 4), shown impacts of the magnetic term on dimensionless amplitude-frequency ratio curve of stabilities assessment of SWCNTs structure in magneto-thermal environment under two elastic foundations. The curve depicted that as magnetic term increases from zero to maximum frequencyratio increases above linearity system. This shows that for the single-walled carbon nanotube structure to gain stability, the magnetic term must be kept at lowest value as control measure to stabilized single-walled nanotube structure.

The above (Figure 5), shown impacts of the thermal term on dimensionless amplitude-frequency ratio curve of stabilities assessment of SWCNTs structure in magneto-thermal environment under two elastic foundations. The curve depicted that as thermal term increases from zero to maximum frequency-ratio increases above linearity system. This shows that for the single-walled carbon nanotube structure to gain stability, the thermal term must be kept at lowest value as control measure to stabilized singlewalled nanotube structure.

The above (Figure 6), shown impacts of different boundary conditions on dimensionless amplitude-frequency ratio curve of stabilities assessment of SWCNTs structure magneto-thermal environment under two elastic foundations subjected to different supports system [16]. The curve depicted that fixed-fixed support has lowest frequency ratio, followed by fixed-simply supported then simple-simple support and fixed free has the highest frequency ratio. However, this reveal that in selecting elastic foundation type, fixed ended support exhibit best foundation type with lowest frequency ratio and can be used to control stability of any foundation.

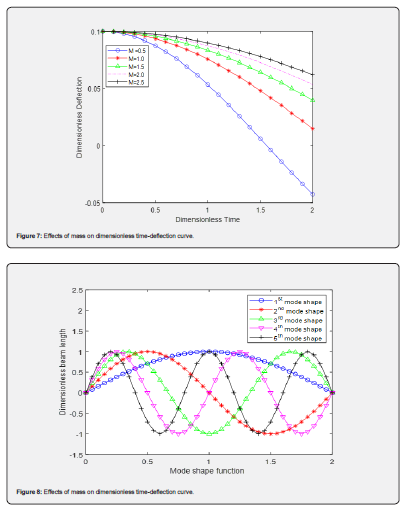
The above (Figure 7), shown impacts of mass on dimensionless time-deflection curve of dynamical response of SWCNTs structure in magneto-thermal environment under two elastic foundations. The curve depicted that as mass increases from zero to maximum frequency of oscillation decreases. This shows that for SWCNTs structure to dynamical response, the mass must be kept at maximum as the nonlinearity system turn into linearity.

The first-five normalized mode shapes of the beams for the nanotube with simple-simple support is shown in (Figure 8). This figure shows the deflections of the beams along the beams’ span at five different dimensionless mode shapes. The natural frequencies show where the maximum vibration will occur, mode shape or natural vibration shape are used in dynamics to describes the deformation that the component would show when vibrating at the natural frequency as the vibration and deformation do not occur until there is an excitation [17].

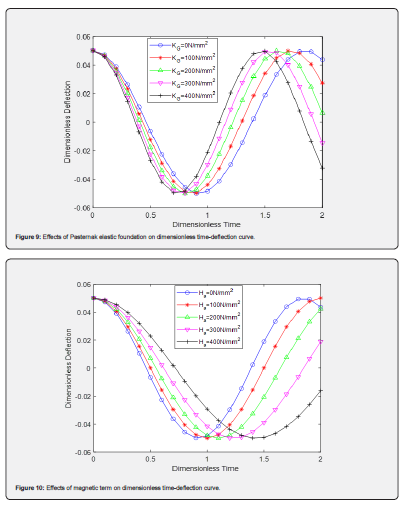
(Figures 9 &10) show the impacts of dimensionless Pasternak elastic foundation and magnetic term on the dynamic response of the studied carbon nanotube. (Figure 9) and (Figure 10) show the impacts of Pasternak elastic foundation and magnetic term on dynamic response. It can be observed from the time-deflection curves that continuous increase in the magnitude of both parameters helps shift the dynamic response of the system from nonlinear to linear.

Conclusion

Theoretical Analysis of Single-walled carbon nanotube embedded in an elastic foundation in a magneto-thermal environment using differential transformation method was investigated. The resulting model equation of motion was converted to ordinary differential equation using Galerkin technique subsequently, differential transform method with cosine-after treatment technique is used to obtain dynamic characteristics response under four different boundaries conditions of the nanotube structure. The results obtained depicts that, linear Winkler-type and Pasternak-type elastic foundation increases from zero to maximum as frequency-ratio decreases meanwhile nonlinear Winkler-type elastic foundation, magnetic and thermal terms increase with increase in frequency ratio. In selecting elastic foundation type, fixed-fixed ended supports exhibit best foundation type with lowest frequency ratio as a control measure for stability analysis of any foundation type.

References

1. Payam S, Hadi AD, Anoushiravan F (2010) Thermo-mechanical Vibration of a Single-walled Carbon Nanotube Embedded in a Pasternak Medium Based on Nonlocal Elasticity Theory: 18^th Annual International Conference on Mechanical Engineering-ISME2010, p. 11-13.
2. Natsuki T, Lei X, Ni Q, Endo M (2010) Vibrational analysis of double-walled carbon nanotubes with inner and outer nanotubes of different lengths. Physics Letters A 374(46): 4684-4689.
3. Ghasemi SE, Gouran S (2022) Nonlinear Analysis on Flow-Induced Vibration of Single-Walled Carbon Nanotubes Employing Analytical Methods. International Journal of Structural Stability and Dynamics 22(11): pp. 2250115.
4. Alibeigloo, Jafarian (2016) Three-Dimensional Static and Free Vibration Analysis of Carbon Nano Tube Reinforced Composite Cylindrical Shell Using Differential Quadrature Method. International Journal of Applied Mechanics 8(3): 1650033.
5. Valipour P, Ghasemi SE, Mohammad RK, Ganji DD (2016) Theoretical analysis on nonlinear vibration of fluid flow in single-walled carbon nanotube. Journal of Theoretical and Applied Physics 10: 211-218.
6. Mohammadimehr M, Alimirzaei S (2016) Nonlinear static and vibration analysis of Euler-Bernoulli composite beam model reinforced by FG-SWCNT with initial geometrical imperfection using FEM. Structural Engineering and Mechanics 59(3): 431-454.
7. Farshidianfar A, Soltani P (2012) Nonlinear flow-induced vibration of a SWCNT with a geometrical imperfection. Computational Materials Science 53(1): 105-116.
8. Soltani P, Saberian J, Bahramian R (2016) Nonlinear Vibration Analysis of Single-Walled Carbon Nanotube with Shell Model Based on the Nonlocal Elasticity Theory. Journal of Computational and Nonlinear Dynamics 11(1): 011002.
9. Mu’tasim S Abdel-Jaber, Ahmad A Al-Qaisia, Nasim K Shatarat (2017) Nonlinear Vibrations of a SWCNT with Geometrical Imperfection Using Nonlocal Elasticity Theory. Modern Applied Science 11(10).
10. Mahmoud MS (2021) Torsional vibration of irregular single-walled carbon nanotube incorporating compressive initial stress effects. Journal of Mechanics 37: 260-269.
11. Yu-Chi S, Tse-Yu C (2021) Free vibration of a single-walled carbon nanotube based on the nonlocal Timoshenko beam model. Journal of Mechanics 37: 616-635.
12. Fatahi-Vajari A , Azimzadeh Z (2018) Analysis of nonlinear axial vibration of single-walled carbon nanotubes using Homotopy perturbation method. Indian Journal of Physics: 92: 1425-1438.
13. Murmu T, Pradhan SC (2009) Buckling analysis of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity and Timoshenko beam theory and using DQM. Physical E: Low-Dimensional Systems and Nanostructures 41(7): 1232-1239.
14. Hassen OM, Mohammad YI (2011) Natural frequencies and mode shapes of initially curved carbon nanotube resonators under electric excitation. Journal of Sound and Vibration 330(13): 3182–3195.
15. Ghorbanpour Arani A, Zarei MS (2014) Nonlinear Nonlocal Vibration of an Embedded Viscoelastic Y-SWCNT Conveying Viscous Fluid Under Magnetic Field Using Homotopy Analysis Method. Journal of Solid Mechanics 6(2): 173-193.
16. Chang TP (2016) Nonlinear Vibration of Single-Walled Carbon Nanotubes Under Magnetic Field by Stochastic Finite Element Method. International Journal of Structural Stability and Dynamics: 16(8): 1550046.
17. Ke L, Li X, Yang Y, Kitipornchai JS (2009) Nonlinear free vibration of embedded double-walled carbon nanotubes based on nonlocal Timoshenko beam theory. Computational Materials Science 47(2): 409-417.