Cooling of Tree Surface Area due to Solar Reflective Coatings
David W Yarbrough*
R&D Engineering, LLC Watertown, USA
Submission: October 28, 2020;Published: November 04, 2020
*Corresponding author:David W Yarbrough, R&D Engineering, LLC Watertown, TN, USA
How to cite this article:David W Y. Cooling of Tree Surface Area due to Solar Reflective Coatings. Eng Technol Open Acc. 2020; 3(4): 555619. DOI: 10.19080/ETOAJ.2020.03.555619
Keywords:Transport control protocol; Acknowledgement limiting; ACK rate limiting; Linux kernel TCP stack
Abbreviations:h, hC: Heat Transfer Coefficient W/m2; I: Solar Flux W/m2; QSOL: Product of I and α W/m2; r: Solar Reflectance; T: Temperature; α: Solar Absorptance; ε: Thermal Emittance; σ: Stefan-Boltzmann Constant 5.67x10-8 W/m2∙K4
Introduction
The application of a high solar reflectance coating to tree trunk surface area reduces the temperature of the surface when exposed to heat input from the sun. Solar reflectance (r) of a surface is a number between 0 and 1 that quantifies the fraction of incoming solar radiation that is reflected by a surface. The solar absorptance (α) is the fraction of solar radiation that is absorbed by the surface. The solar absorptance is 1 – r. Coatings with solar reflectance’s above 0.8 are often referred to as “cool coatings”. The α value foe cool coating is generally less than 0.2. High solar reflectance, cool, coatings have found use is reducing the maximum day-time temperature of roofs (cool-roof coatings). The same technology has potential use for the reduction of maximum day-time temperature of tree-surface area. A reduction of maximum tree surface temperatures contributes to the long-term health of the tree.
Heat Balance to Calculate Temperatures
The surface temperature of a surface exposed to solar radiation, I , can be calculated from a heat balance as shown in the ASTM Standard Practice E 1980 [1]. The heat balance as shown by the following equation includes the input of heat due to solar radiation (α∙I), thermal radiation exchange between the tree surface and the sky (ε.σ.(Ts4−TSKY4)), and heat exchange by conduction and convection between the tree surface and the surrounding air (hC.(TS–TAIR)).
Since radiative transport is involved, the temperatures are expressed on the absolute or Kelvin scale (K).
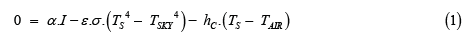
All of the terms in Equation are specified except TS, the tree surface temperature on the Kelvin scale. T(°F) is obtained from T(K) by Equation 2.
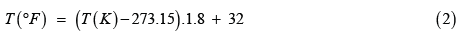
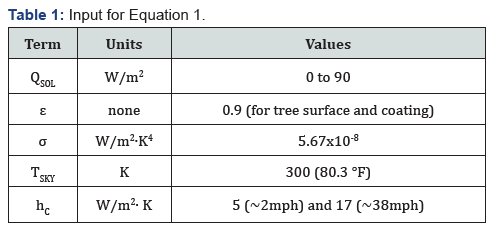
TS is the “unknown” in Equation 1. The values for TS that satisfy Equation 1 can be determined numerically by assigning trial values for TS until the right side of Equation 1 equals zero. The TS values depend on the numerical values of all of the other terms in the equation. The values selected for the terms in Equation 1 are shown in Table 1. The values selected are guided by the discussion in E 1980. The combination α∙I will be shown as QSOL to signify heat input from the sun in W/m2. The wind speeds shown in the hc line are approximations.
Results for Tree-Surface Temperatures
Table 2 contains surface temperature, TS, that satisfy Equation 1. for the listed TAIR, QSOL, ε and hC values. The smaller hc value (5) represents very little air movement. An increase in air speed to attain hC 17 results in significant cooling of the tree surface (212.5 to 160.9, for example).
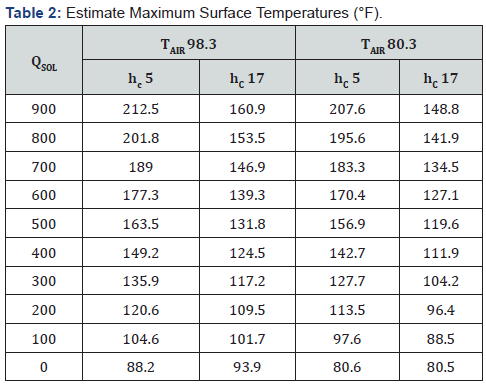
Table 3 contains the results of subtracting TAIR from each of the entries in Table 2. The results show that the air speed (indicated by the increase in hc ) has a major impact on the tree surface temperature (cooling effect of the moving air). The horizontal line shows that temperatures for a coating with high r (r=0.9) and high solar flux (1000). The tree surface temperature is close to the air temperature even though the solar flux is very high. The negative values occurring at night (QSOL=0) represent cooling by radiation to the night sky. The temperatures in Table 3 are °F.
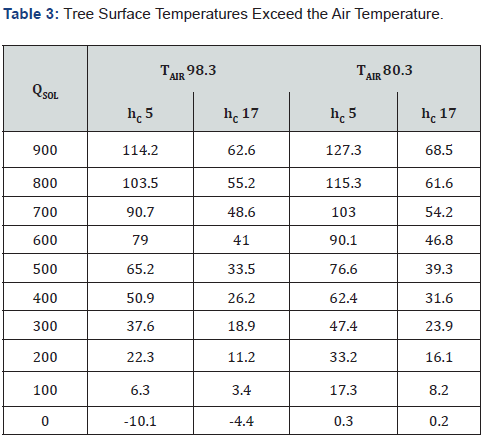
Table 4 contains temperature reductions due to changing the solar absorptance (a) from 0.9 to either a=0.1 or a=0.2. These results are based on equations that are derived from the data shown in Table 2 and Figure 1.
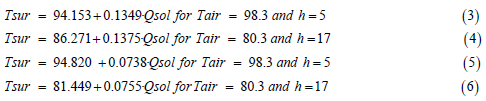

The temperature reductions due to coating in Table 4 are in °F. The uncoated surface is assigned a solar absorption of 0.9. Two values for the solar absorption of coated surface were evaluated to show the range anticipated for the temperature reduction due to coating.
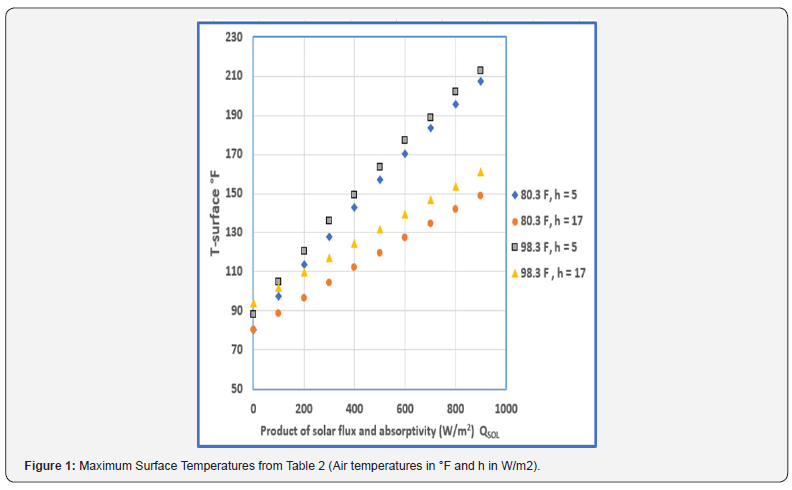
Figure 1 contains the surface temperatures for the four cases that were considered. The graphical results show the distinct division for the two heat transfer coefficients (h or hC) for which results were calculated. The Surface temperatures are directly proportional to the absorbed solar radiation when the other terms remain constant.
Discussion
The calculations presented here do not include heat conducted to the interior of the tree or the cooling effect of evaporation. Bark temperature of 130°F have been reported for wild cherry trees by Sheppard et al. [2] for air temperatures in the range considered here but unknown solar flux. The 130°F observation corresponds to the current results with solar flux of ~500W/m2 and r = 0.2. The high temperatures obtained in the present calculation result from severe conditions: high solar flux and very little wind.
References
- ASTM E (1980) Standard Practice for Calculating Solar Reflectance Index ofHorizontal and Low-Slope Opaque Surfaces. Annual Book of ASTM Standards, 4(6).
- Sheppard J, Morhart C, Spieckler H (2016) Bark surface temperature measurements on the boles of wild cherry (Prunus avium) grown within an agroforestry system. Silva Fennica50(3).






























