Non-Dominated Sorting Moth Flame Optimizer: A Novel Multi-Objective Optimization Algorithm for Solving Engineering Design Problems
Pradeep Jangir1* and Indrajit N Trivedi 2
1Department of Electrical Engineering, Rajasthan Rajya Vidyut Prasaran Nigam Losal-Sikar, India
2Department of Electrical Engineering, Government Engineering College, India
Submission: April 07, 2018; Published: July 05, 2018
*Corresponding author: Pradeep Jangir,Junior Engineer, Rajasthan Rajya Vidyut Prasaran Nigam Losal-Sikar, Rajasthan, India, Email: pkjmtech@gmail.com
How to cite this article: Pradeep J, Indrajit N T. Non-Dominated Sorting Moth Flame Optimizer: A Novel Multi-Objective Optimization Algorithm for Solving Engineering Design Problems. Eng Technol Open Acc. 2018; 2(1): 555579. 10.19080/ETOAJ.2018.02.555579
Abstract
This novel article presents the multi-objective version of the recently proposed Moth-flame optimizer (MFO) known as Non-Dominated Sorting Moth Flame Optimizer (NSMFO). This proposed NSMFO algorithm works in such a manner that it first collects all non-dominated Pareto optimal solutions achieved till the evolution of last iteration limit. The best solutions are then chosen from the collection of all Pareto optimal solutions using a crowding distance mechanism based on the coverage of solutions as navigation strategy to guide moths towards the dominated regions of multi-objective search spaces. For validate the efficiency and effectiveness of proposed NSMFO algorithm is applied to a set of standard unconstrained, constrained and engineering design problems. The results are verified by comparing NSMFO against Multi objective Colliding Bodies Optimizer (MOCBO), Multi objective Particle Swarm Optimizer (MOPSO), non-dominated sorting genetic algorithm II (NSGA-II) and Multi objective Symbiotic Organism Search (MOSOS).The results of proposed NSMFO algorithm validates its efficiency in terms of Execution Time (ET) and effectiveness in terms of Generalized Distance (GD), Diversity Metric (DM) on standard unconstraint, constraint and engineering design problem in terms of high coverage and faster convergence.
Keywords: Non-dominated; Crowing distance; NSMFO algorithm; Multi-objective algorithm; Economic constrained emission dispatch
Abbrevations: NSMFO: Non-Dominated Sorting Moth Flame Optimizer; MOCBO: Multi Objective Colliding Bodies Optimizer; MOPSO: Multi Objective Particle Swarm Optimizer; MOSOS: Multi Objective Symbiotic Organism Search; ET: Execution Time; GD: Generalized Distance; DM: Diversity Metric
Introduction
Optimization is a work of achieving the best result under given limitation or constraints. Now a day, optimization is used in all the fields like construction, manufacturing, controlling, decision making, prediction etc. The final target is always to get feasible solution with minimum use of resources. In this field computers make a revolutionary impact on every field as it provides the facility of virtual testing of all parameters that are involved in a particular design with less involvement of human efforts, benefits in less time consuming, human efforts and wealth as well.
Today we use computer-aided design where a designer designs a virtual system on computer and gives only command to test all parameters involved in that design without even the need for a single prototype. A designer only to design and simulate a system and set all the parameter limitation for the computer.
Computer-aided design technique becomes more effective with the additional feature of auto-generation of solutions after it’s mathematically formulation of any system or design problem. Auto generation of solution, this feature is come into nature with the development of algorithms. In past years, real world designing problems are solved by gradient descent optimization algorithms. In gradient descent optimization algorithm, the solution of mathematically formulated problem is achieved by obtaining its derivative. This technique is suffered from local minima stagnation [1,2] more time consuming and their solution is highly dependent on their initial solution.
The next stage of development of optimization algorithms is population based stochastic algorithms. These algorithms had number of solutions at a time so embedded with a unique feature of local minima avoidance. Later population-based algorithms are developed to solve single objective at a time either it may be maximization or minimization on accordance the problems objective function. Some popular algorithms for single objective problems are Grey wolf optimizer (GWO) [3], Bat algorithm (BA) [4], Particle swarm optimization (PSO) [5], Ant colony optimization (ACO) [6], Genetic algorithm (GA) [7], Cuckoo search (CS) [8], Mine blast algorithm (MBA) [9], Krill Herd (KH) [10], Interior search algorithm (ISA) [11] etc. These algorithms have capabilities to handle uncertainties [12], local minima [13], misleading global solutions, better constraints handling etc [14,15]. To overcome these difficulties different algorithms are enabled with different powerful operators. As mention above here is only objective then it is easy to measure the performance in terms of speed, accuracy, efficiency etc. with the simple operational operators.
In general, real world problems are nonlinear and multiobjective in nature. In multi-objective problem there may be some objectives are consisting of maximization function while some are minimization function. So now a day, multi-objective algorithms are in firm attention.
Let’s take an example of buying a car, so we have many objectives in mind like speed, cost, comfort level, space for number of people riding, average fuel consumption, pick up time required to gain particular speed, type of fuel requirement either it is diesel driven, petrol driven or both etc. To simply understand multiobjective problem, from Figure 1, we consider two objectives, first cost and second comfort level. So we go for sole objective of minimum cost possible then we have to deny comfort level objective and vice-versa. It means real word problems are with conflicting objectives. So as, we are disabled to find an optimal solution like single objective problems. About multi-objective algorithm and its working is detailed described in next portion of the article.

Figure1 Car-buying decision-making problem (Hypothetical Optimal solutions). The No free launch [16] theorem that logically proves that none of the only algorithm exists equally efficient for all engineering problem. This is the main reason that it allows all researcher either to propose new algorithm or improve the existing ones. This paper proposed the multi-objective version of the well-known moth flame optimizer (MFO) [17]. In this paper non-sorted MFO (NSMFO) is tested on the standard un-constraint and constraint test function along with some well-known engineering design problem, their results are also compared with contemporary multi-objective algorithms Multi objective Colliding Bodies Optimizer (MOCBO) [18], Multi objective Particle Swarm Optimizer (MOPSO) [19,20], Non-dominated Sorting Genetic Algorithm (NSGA) [21-23], non-dominated sorting genetic algorithm II (NSGA-II) [24] and Multi objective Symbiotic Organism Search (MOSOS) [25] that are widely accepted due to their ability to solve real world problem.
The structure of the paper can be given as follows: - Section 2 consists of literature; Section 3 includes the proposed novel NSMFO algorithm; Section 4 consists of competitive results analysis of standard test functions as well as engineering design problem and section 5 includes real world application, finally conclusion based on results and future scope of work is drawn.
Literature Review
As the name describes, multi-objective optimization handles simultaneously multiple objectives. Mathematically minimize/ maximize optimization problem can be written as follows:
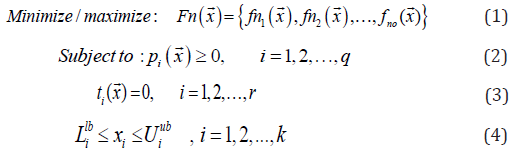
Where q is the number of inequality constraints, r is the number of equality constraints is the number of variables, pi is the ith inequality constraints, no is the number of objective functions, ti indicates the ith equality constraints, and [Lil,Uiub]are the boundaries of ith variable.
Obviously, relational operators are ineffective in comparing solutions with respect to multiple objectives. The most common operator in the literate is Pareto optimal dominances, which is defined as follows for minimization problems:
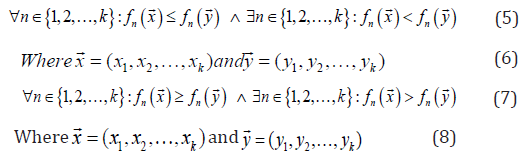
These equations show that a solution is better than another in a multi-objective search space if it is equal in all objectives and better in at least one of the objectives. Pareto optimal dominance is denoted with ≺ and ≻. With these two operators’s solutions can be easily compared and differentiated.
Population based multi-objective algorithm’s solution consists of multiple solutions. But with multi-objective algorithm we cannot exactly determine the optimal solution because each solution is bounded by other objectives or we can say there is always conflict between other objectives. So the main function of stochastic/population based multi-objective algorithm is to find out best trade-offs between the objectives, so called Pareto optimally set [26-28].
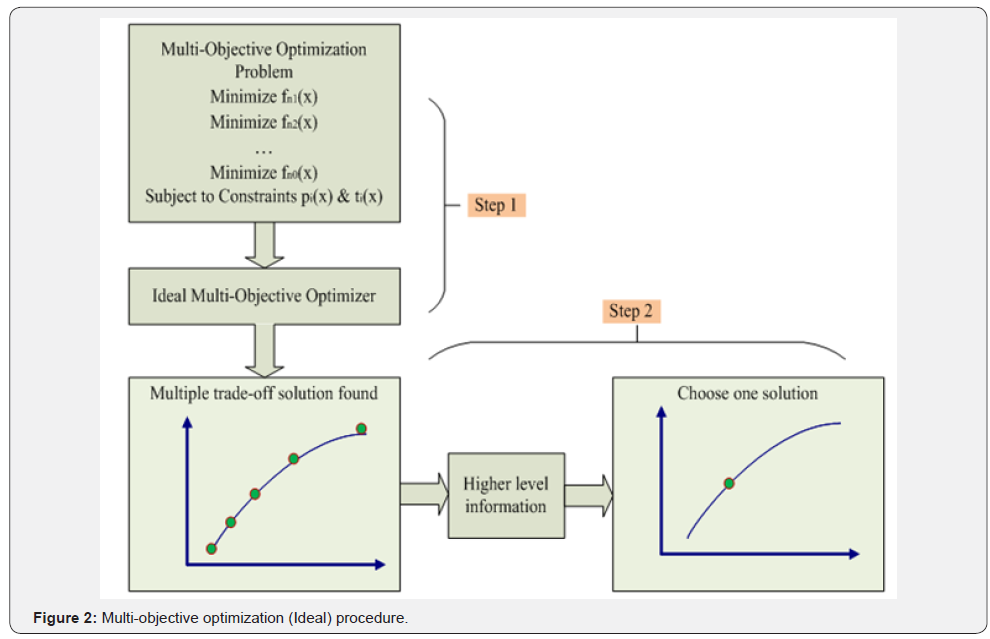
The principle of working for an ideal multi-objective optimization algorithm is as shown in Figure2.
Step No. -1 Find maximum number of non-dominated solution according to objective, it expresses the number of Pareto optimal set so as shows higher coverage
Step No. -2 Choose one of the Pareto optimal solution using crowding distance mechanism that fulfils the objectives.
Now a days, recently proposed sole objective algorithms are equipped with powerful operators to provide them a capability to solve multi-objective problems as well. In the same manner we proposed NSMFO in a hope that it will perform efficiently for multiobjective problems. These are: Multi-objective GWO [29], Multiobjective Bat Algorithm [30], Multi-objective Bee Algorithm [31], Pareto Archived Evolution Strategy (PAES) [32], Pareto-frontier Differential Evolution (PDE) [33], Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D) [34], Strength- Pareto Evolutionary Algorithm (SPEA) [35,36] and Multi-objective water cycle algorithm with unconstraint and constraint standard test functions [37,38].Performance measurement for approximate robustness to Pareto front of multi-objective optimization algorithms in terms of coverage, convergence and success metrics.
The computational complexity of NSMFO is order of O(mn2 ) where N is the number of individuals in the population and M is the number of objectives. The complexity for other good algorithms in this field: NSGA-II, MOPSO, SPEA2 and PAES areO(mn2 ) . However, the computational complexity is much better than some of the algorithms such as NSGA and SPEA which are ofO(mn3 ) .
Non-Dominated Sorting Moth Flame Optimizer (NSMFO)
Moth-flame optimizer (MFO) algorithm with sole objective was proposed by Mirjalili Seyedali in 2015 [17]. It is basically a stochastic population based, nature inspired algorithm. In this algorithm the basic strategy of navigation for travelling long distances in straight direction having a constant angle w.r.t moon (flame) is utilized by insects (Moths) in night. However, this strategy efficiently works only for the targeted flame is far distance away from the moths but fails if flame is nearer. Generally, if flame is far from moth then it is easy for the moths to keep the constant angle from it, but in opposite case when flame is nearer then the angle continuously decreasing and finally moths tends to dip into flame (targeted optimal solution).
Basic working of NSMFO algorithm is as follows
Stage 1:
a. First of all, initialize the population of moths
b. Randomly generated sets of moths & flames are represented in matrix for convenience to understand
c. Then fitness of moths & flames is calculated on an according as objective function
Stage 2:
a. Position of moths in a spiral path is a function of the position of moths and flames
b. The value of absolute distance is achieved which is basically a distance between the current best solution to the final optimal solution
c. Then exact position of moths & flames is achieved which is a mathematical spiral function of with a product of actual distance between them and an addition of the position of flame.

Where, J is a function that generates a random population of moths and their fitness values. Q is a function, moves the moths around unknown search space and G comes true when termination criterion fulfilled else false comes.
Step 3
a. Termination counter in integrated to limit/forcefully stop the search in uncertain search space (max. iteration counter to forcefully converge the search to optimal one)
b. Size of the flame matrix is continuously reduced over the course of iteration due to directed search to find global best solution (Quick sorting is used to provide directional search)
c. Continuously position of the moths and flames is updated via a spiral function equation for each iteration
Step 4
a. Likewise, multi-objective optimization the NSMFO algorithm is made to capable to store the pareto optimal solutions in a collection set and make it as flexible to change solution over the course of iteration
b. Solution is assigned a rank according to their ability as if a solution is not dominated by other solution is assigned rank1, dominated by only solution assigned rank 2 and so on & if collection set is full over predefined size then some solutions that are dominated in nature are directed to be out from the collection set according to the crowding distance mechanism.
This collection set is similar to the term achieve used in MOSOS and NSGA-II. It is a repository to store the best non-dominated solutions obtained so far. The search mechanism in NSMFO is very similar to that is MFO, in which solutions are improved using moths. Due to the existence of multiple best solutions, however, the best moth should be chosen from the collection set.
In order to select solutions from the archive to establish tunnels between solutions, we employ a leader selection mechanism. In this approach, the crowding distance between each solution in the archive is first selection and the number of solutions in the neighbourhood is counted as the measure of coverage or diversity. We require the NSMFO to select solutions from the less populated regions of the archive using the following equation to improve the distribution of solutions in the archive across all objectives.
This subsection proposes multi-objective version of the MFO algorithm called NSMFO. The non-dominated sorting has been of the most popular and efficient techniques in the literature of multi-objective optimization. As its name implies, non-dominated sorting sort Pareto optimal solutions based on the domination level and give them a rank. This means that the solutions that are not dominated by any solutions is assigned with rank 1, the solutions that are dominated by only one solution are assigned rank 2, the solutions that are dominated by only two solutions are assigned rank 3, and so on. Afterwards, solutions are chosen to improve the quality of the population base on their rank. The better rank, the higher probability to be chosen. The main drawback of non-dominated sorting is its computational cost, which has been resolved in NSGA-II.
The success of the NSGA-II algorithm is an evidence of the merits of non-dominated sorting in the field of multi-objective optimization. This motivated our attempts to employ this outstanding operator to design another multi-objective version of the MFO algorithm. In the NSMFO algorithm, solutions are updated with the same equations presented in equation (12) In every iteration, however, the solutions to have optimal position of moths and flames are chosen using the following equation:

Where c is a constant and should be greater than 1 and i Rank is the rank number of solutions after doing the non-dominated sorting.
This mechanism allows better solutions to contribute in improving the solutions in the population. It should be noted that non-dominated sorting gives a probability to dominated solutions to be selected as well, which improves the exploration of the NSMFO algorithm.
Constraint handling approach
With the extended literature survey, we find that the population-based algorithms are the common way to solve the multi-objective problems as they are more commonly provides the global solution and capable of handling both continuous and combinational optimization problem with a very high coverage and convergence. Multi-objective problems are subjected to various types of constraints like linear, non-linear, equality, inequality etc. So, with these problems embedded it is very difficult to find simple and good strategy to achieve considerable solutions in the acceptable criterion. So in this paper NSMFO algorithm uses a very simple approach to get feasible solutions. In this mechanism, after generating number of solutions at each generation, all the desirable constraint checked and then some solution that fulfils the criterion of acceptable solution are selected and collected them in achieve. Afterward non-dominated solutions added in archive as we find more suitable solution to get acceptable solution. So as if achieve is full then less dominated solutions are removed. Finally, according to crowing distance mechanism all these solutions (more suitable position of moths and flames) from archive is selected to get desired solution (figure 3).
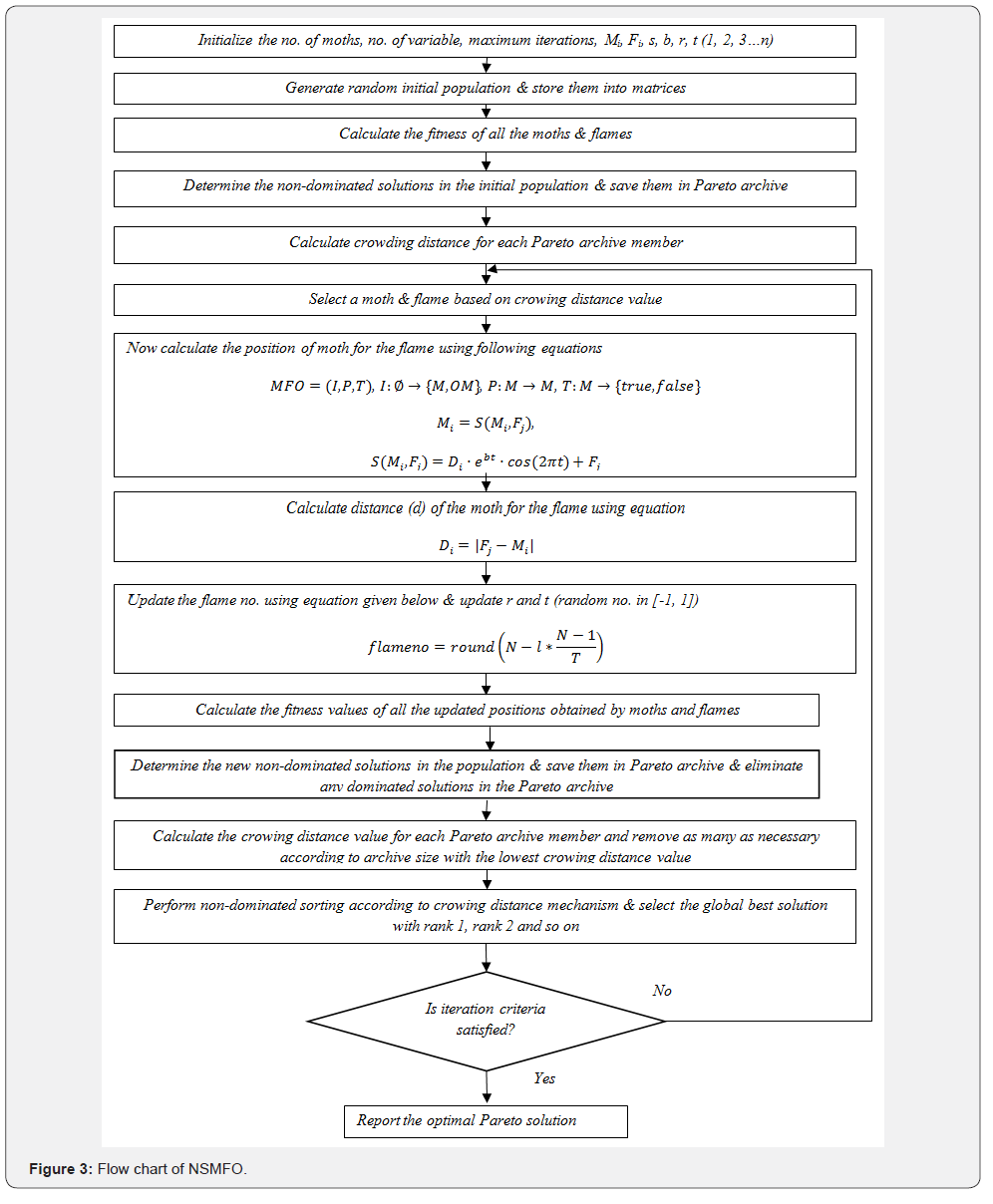
Results Analysis on Test Functions
For determine the performance of proposed NSMFO algorithm is applied to:
a. A set of unconstraint and constraint standard multiobjective test functions
b. Tested on well-known engineering design problems
c. Non-linear, highly complex practical application known as formulation of economic constrained emission dispatch (ECED) with stochastic integration of wind power (WP) in the next section
NSMFO algorithm is tested on seventeen different multiobjective case studies, including eight unconstrained test functions, five constrained test functions, and four real world engineering design problem, later algorithm is applied to the main application economic constrained emission dispatch with wind power (ECEDWP). These can be classified into four groups given below:
a. Standard multi-objective unconstrained test functions (KUR, FON, ZDT1, ZDT2, ZDT3, ZDT4, SCHN1, and SCHN2)
b. Standard multi-objective constrained test functions (TNK, OSY, BNH, SRN, and CONST)
c. Real world engineering multi-objective design problem (Four bar truss design, welded beam design, speed reducer and disk brake design problem)
d. Modelling of ECEDWP problem
Mathematical representation of these standard test functions are given in Appendix
1. (Multi-objective unconstrained test functions),
2. (Multi-objective constrained test functions),
3. (Engineering multi-objective design problem)
with distinct characteristics like non-linear, non-convex, discrete pareto fronts and convex etc. are selected to measure the performance of proposed NSMFO algorithm.
To deal with real world engineering design problem is really a typical task with unknown search space, in this article we include four different engineering problems are considered and performance is compared with various well-known algorithms like MOWCA, NSGA-II, MOPSO, PAES and μ -GA multi-objective algorithms. Each algorithm is separately runs fifteen times and numeric results are listed in tables below. To measure the quality of obtained results we match their coverage of obtained true pares to front with respect to their original or true pareto fronts.
For numeric as well as qualitative performance of purposed NSMFO algorithm on various case studies we consider Generational Distance (GD) given by Veldhuizen in 1998 [39] for measuring the deviation of the distance between true pareto front and obtained pareto front, Diversity matric (Δ) also known as matrix of spread to measure the uniformly distribution of non-dominated solution given by Deb [24] and Metric of spacing (S) to represent the distribution of non-dominated distribution of obtained solutions by purposed algorithm given by Schott [40].
The mathematical representation of this performance indicating metric are as follows:

Where di shows the Euclidean distance (calculated in the objective space) between the ith Pareto optimal solution achieved and the nearest true Pareto optimal solution in the reference set, nPFs is the total number of achieved Pareto optimal solutions.

Where, , l m d d are Euclidean distances between extreme solutions in true pared to front and obtained pared to front. i d Shows the Euclidean distance between each point in true Pareto front and obtained Pareto front. nPFs and ‘d’ are the total number of achieved Pareto optimal solutions and averaged distance of all solutions

Where “d” is the average of all i d , nPFs is the total number of achieved Pareto optimal solutions, and
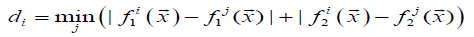
for all i,j=1,2,…,n. Smallest value of “S” metric gives the global best non-dominated solutions are uniformly distributed, thus if numeric value of i d and d are same then value of “S” metric is equal to zero.
Results on unconstrained test problems
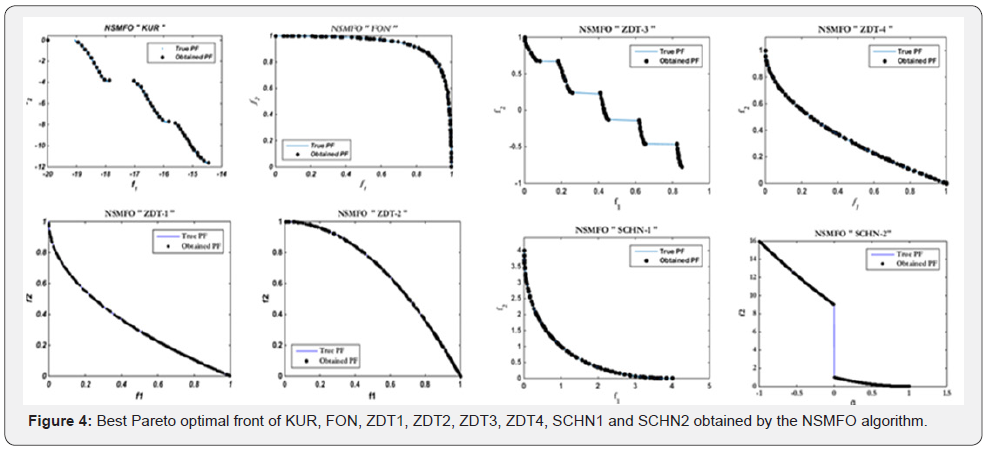
Like as above mentioned, the first set of test problems consist of unconstrained standard test functions. All the standard unconstrained test functions mathematical formulation is shown in Appendix A. Later, the numeric results are represented in Table 1 and best optimal Pareto front is shown in Figure4.
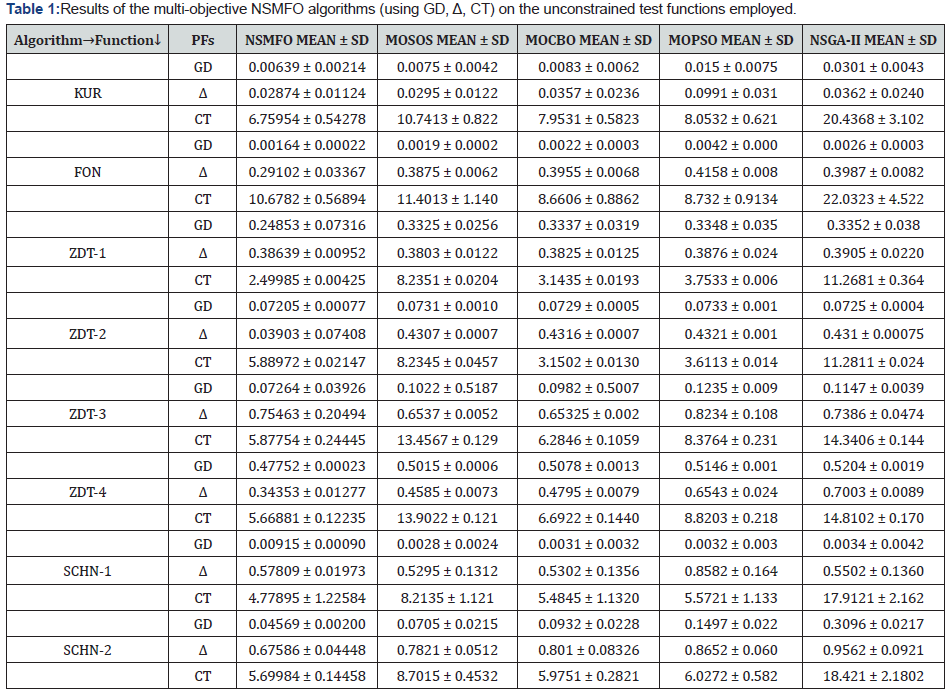
All the statistical results are shown Table 1 suggests that the NSMFO algorithm effectively outperforms with most of the unconstraint test functions compare to the MOSOS, MOCBO, MOPSO and NSGA-II algorithm. The effectiveness of proposed non-dominated version of MFO (NSMFO) can be seen in the Table 1, represents a greater robustness and accuracy of NSMFO algorithm in terms of mean and standard deviation with the help of GD, diversity matrix along with computational time. However, proposed NSMFO algorithm shows very competitive results in comparison with the MOPSO, MOCBO and MOSOS algorithms and in some cases these algorithms performs better than proposed one. Pareto front obtained by proposed NSMFO algorithm shows almost complete coverage with respect to true pareto front (Figure4).
Results on constrained test problems
The next set of standard test functions consisting of constrained functions. For constrained test function it should be necessary that NSMFO algorithm has a capability of handling constraints so algorithm is equipped with a death penalty function to search agents that violate any of the constraints at any level [41]. For comparing the results of different algorithms, we have utilized GD and Δ metrics (Table 2).
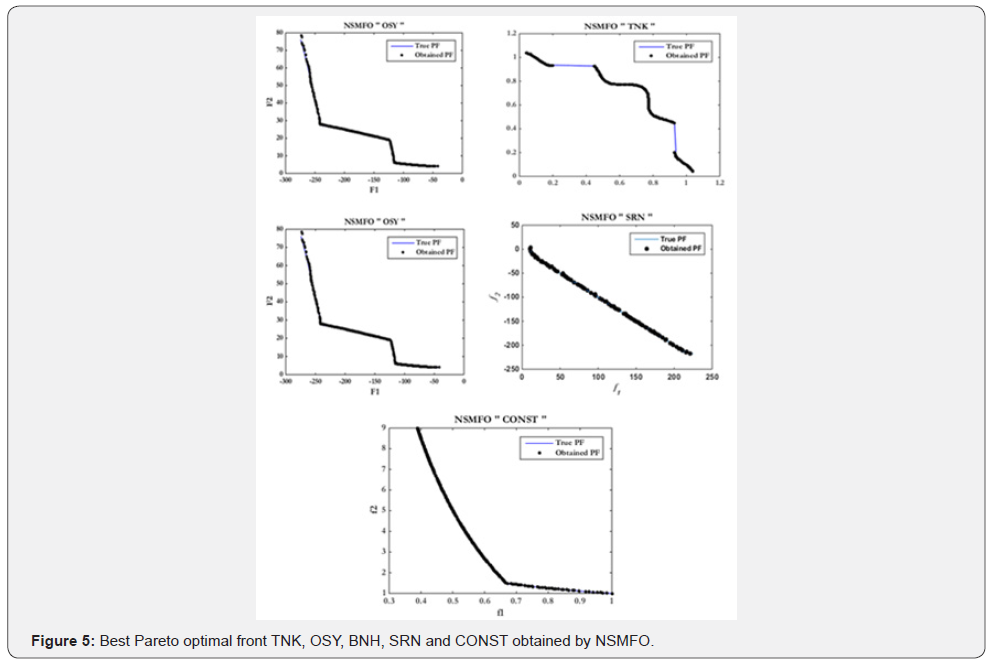
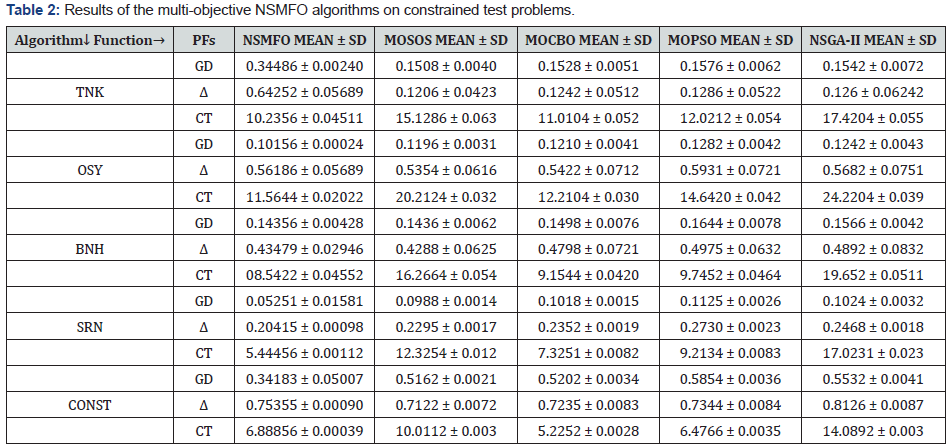
Table 2 suggests that the NSMFO algorithm comparatively performs better than other four algorithms for most of the standard constrained test functions employed. The best Pareto optimal fronts in Figure 5 also helps in proving since all the Pareto optimal solutions exactly follow the true Pareto fronts obtained from by NSMFO algorithm.
CONST function consists of concave front with linear front, OSY is similar to CONST but consists of many linear regions with different slops while TNK almost similar to wave shaped. These also suggest that NSMFO algorithm has a capability to solve various type of constraint problem. All the constraint test functions are mathematically given in Appendix B.
Results on constrained engineering design problems:
The third set of test functions is the most complicated one and consists of four real engineering design problems. Mathematical model of all the four engineering design problem are given in Appendix C. Same as before both GD and diversity matrix is employed to measure the performance of NSMFO algorithm with respect to other algorithms to solve them, numeric results are given in Table 3 and Figure 6 shows the best optimal front obtained by NSMFO algorithm.
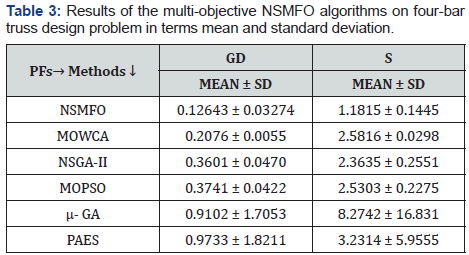
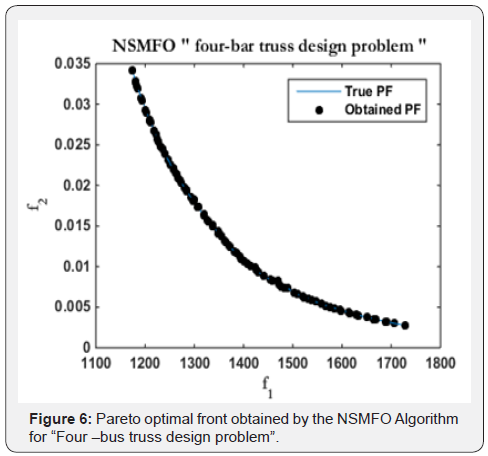
Four-bar truss design problem: The statistical results of four bar truss design problem [42] in given in Table 3 and best optimal front is given in Figure 6 It consists of two minimization objectives displacement and volume with four design control variable mathematically given in Appendix C (Figure 7).
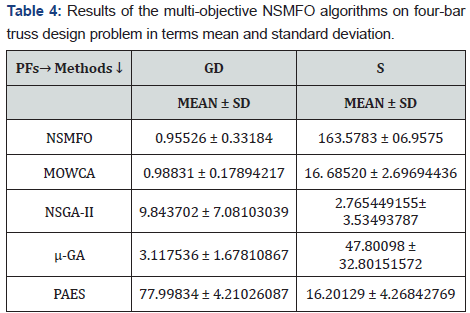
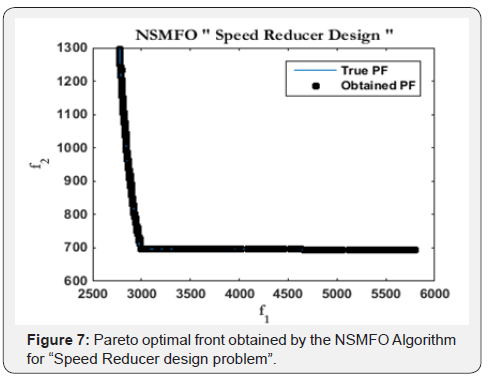
Speed-reducer design problem: The statistical results of speed reducer design problem [43] is given in Table 4 and best optimal front is given in Figure 7 It is a well-known mechanical design problem consists of two minimization objectives stress and weight with seven design control variable mathematically given in Appendix C.
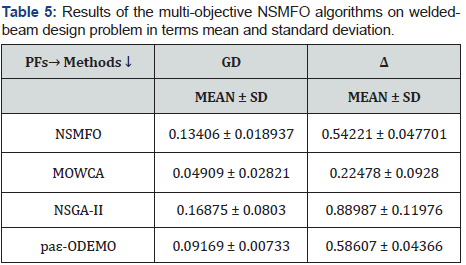
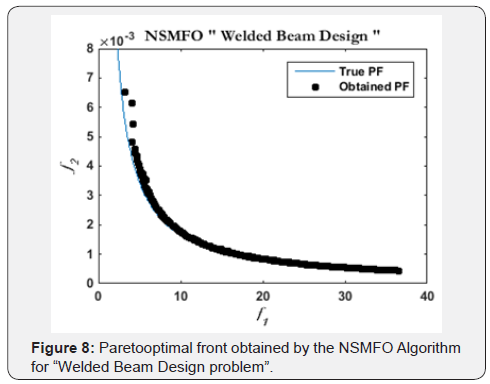
Welded-beam design problem: The statistical results of welded beam design problem [44] is given in Table 5 and best optimal front is given in Figure 8. It is a well-known mechanical design problem consists of two minimization objectives fabrication cost and deflection of beam with four design control variable mathematically given in Appendix C.
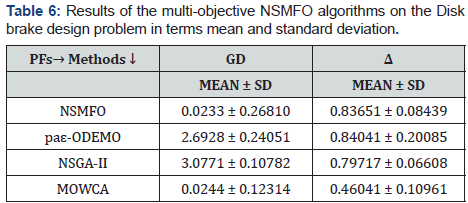
Disk brake design problem: The statistical results of welded beam design problem [44] is given in Table 6 and best optimal front is given in Figure 9. It is a well-known mechanical design problem consists of two minimization objectives stopping time and mass of brake of a disk brake with four design control variable mathematically given in Appendix C.
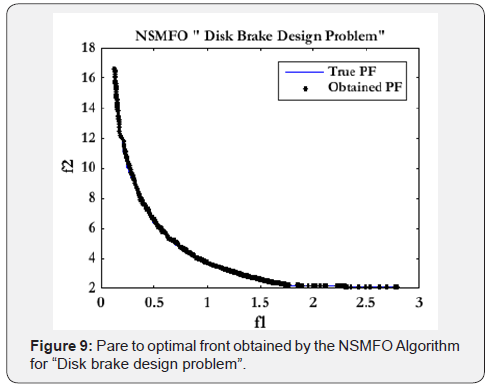
Due to high complexity of engineering design problem it is really hard to gain results alike true pareto front but we can clearly see that optimal pareto obtained by NSMFO algorithm is covers almost whole solutions that are the actual/true solutions of an engineering design problem. From all above testedfunction we can conclude that problem either it consists of constraints or unconstraint problem NSMFO algorithm shows its capability to solve any kind of linear, non-linear and complex real world problem. So in the next section we attached a highly non-linear complex real problem to show its effectiveness regarding the real world complex application with many objectives.
Formulation of economic constrained emission dispatch (ECED) with integration of wind power (WP)
Mathematical formulation of wind power: In case of wind power generation the Output power of wind generator is calculated with the help of a stochastic variable wind speed υ (meter/seconds). Wind speed is a variable function so there probability distribution plays a very important role. Wind speed mathematically formulated as two-parametric Weibull distribution function, probability density function (PDF) and cumulative distribution function (CDF) as follows:
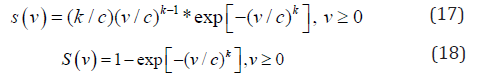
Where, S(v) and s(v) are CDF and PDF respectively. Shape factor and scale factor are k and c respectively.
The wind speed and output wind power are related as:
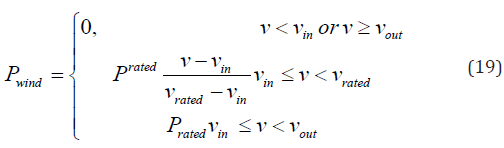
Where, rated v and rated P are the rated speed of wind and rated power output. out v and in v are cut-out and cut-in speed of wind respectively. The CDF of wind P in the boundary of [0, rated P ] on an accordance with the speed range of wind can be formulated as:

Above equation is very meaningful to calculate the ECED problems with speculative wind power with variable speed.
Modelling of ECEDWP problem: As wind power is formulated as system constraint, sothe objective function of economic emission dispatch problem (EEDP) stays on unchanged as classical EEDP:Fuel cost objective is given by:
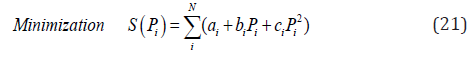
Where, the thermal power generators cost coefficients are ai,bi,ci for ith generator, Sum of the total fuel cost of the system and N is the total number of generators.
Total Emission is calculated by:
Minimization E P=

Where αi, βi, γi, δi and ϕi are emission coefficients with valve point effect taking into consideration for ith thermal generator.
System constraints: As wind power generation is considered as system constraint with the summation of stochastic variables the classical power balance constraint changes to fulfil the predefined confidence level.
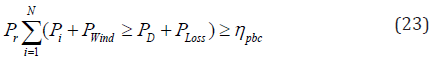
Where, ηpbc is confidence level that a power system must follow the load demand and so as it is selected nearer to unity as values lesser than unity represents high operational risk. Ploss represents system losses can be calculated by B-coefficient method given below:

So as to change above described power balance constrained equation into deterministic form can be solved as:
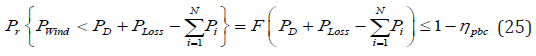
Assume that the wind turbine have same speed and same direction and combination of Eqs. (25), the power balance constraint is represented as:
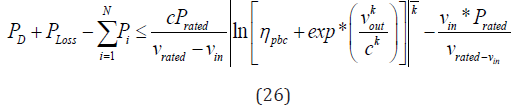
Reserve capacity system constraint: So as to reduce the impact of stochastic wind power on system, up and down spinning reserve needs to be maintained [22]. Such reserve constraints formulated as [15] and [16] respectively:
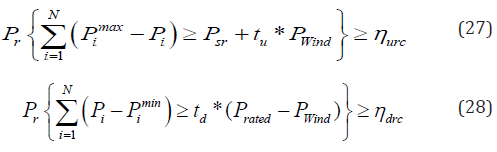
Where, sr Psr represents the reserve demand of conventional thermal power plant system and it generally keeps the maximum value of thermal unit, Pimax and Pimin are maximum and minimum output level of operational generators of ith unit, ηdrc and ηurc are predefined down and upper confidence level parameter respectively, tu and td are the demand coefficients of up and down spinning reserves
Generational capacity constraint: The real output power is bounded by each Generators upper and lower bounds given as:
.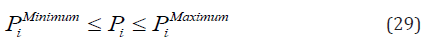
40-Operational Thermal Generating Unit
Case study I- 40 thermal-generator lossless system without wind power
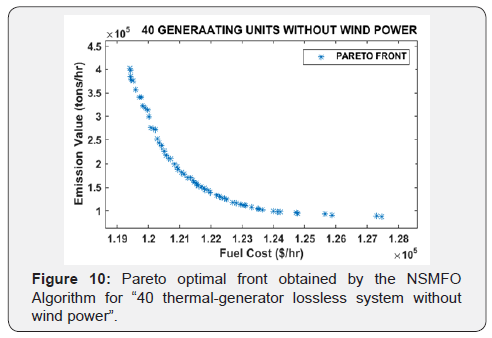
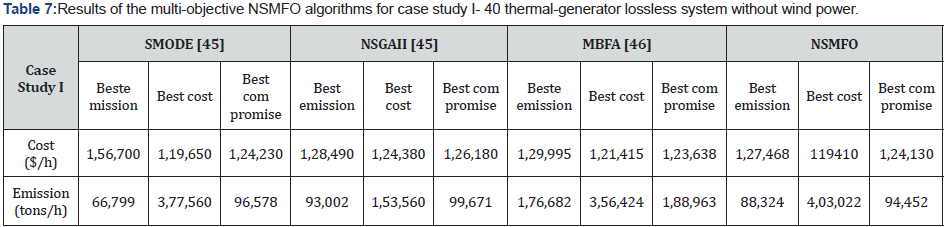
In this case forty operational generating unit is consider without integration of wind power means all the generating units are coal fired. Input parameters like generators operating limit, fuel cost coefficients and emission coefficients are given in Appendix D extracted from [45]. System is considered lossless and its solution is compared with three well known multi-objective algorithms like SMODE [45], NSGA-II [45] and MBFA [46] in terms of various objectives such as best cost, best emission and best compromise between both objectives. Best compromise solution is then obtained by the fuzzy based method [47]. Total power demand for this system is 10500 MW. Results obtained by NSMFO algorithm is added to Table 7 and best Pareto front obtained by NSMFO algorithm is represented in Figure 10.
Case study II- 40 thermal-generator lossless system with wind power
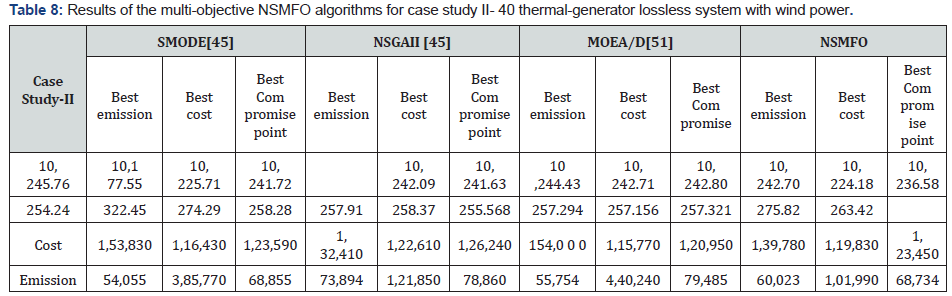
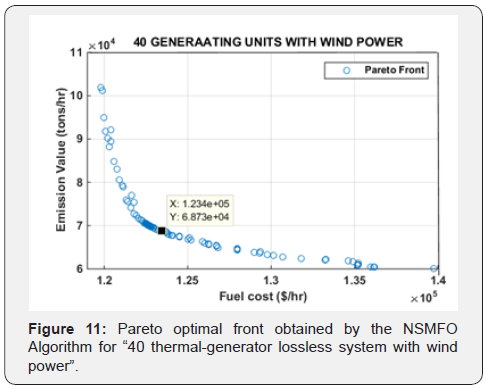
All the conditions are remaining same as case study I like input parameters and power demand. While integrating with wind power plant, the total rated output power of wind farm is set to 1000 MW [45,47]. Statistical results obtained by NSMFO algorithm is reported in Table 8 [51] and best optimal front is represented in Figure 11.
Result & Discussion
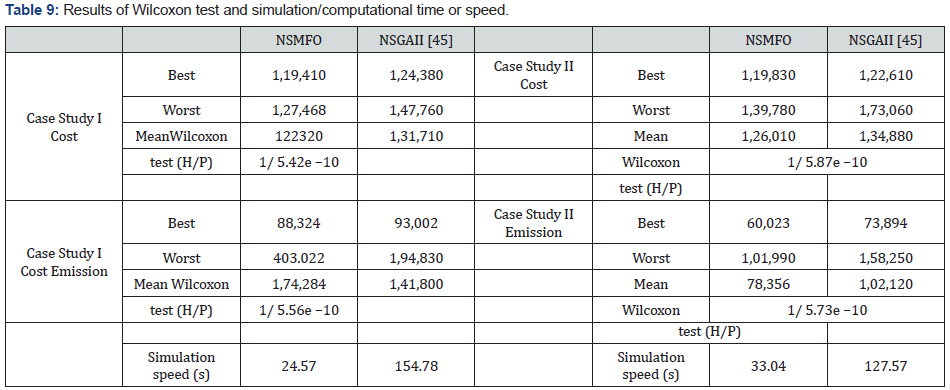
In almost all the cases that we consider in this article where NSMFO algorithm proves its effectiveness in both respects quantitative and qualitative. From plots also evident that NSMFO algorithm follows the exact pareto front similar to the true pareto front for all constrained, unconstrained and complex engineering design problem. So as for real world application of economic emission dispatch problem and its integration with stochastic wind power generation [48-51]. So, for this application Wilcoxon test (statistical test) is performed. In Table 9 the signed rank test is presented in forth row of each results whereas the calculation time is represented in third row. For this test null hypothesis cannot be rejected at 5% level for numeric value ‘0’ while null hypothesis is rejected at 5% level with the value of ‘1’. Where NSMFO algorithm performs superior to other algorithms that are considered for comparative purpose. NSMFO algorithm shows good performance in both coverage and convergence as main mechanism that guarantee convergence in MFO and NSMFO are continuously shrink its virtual limitation in the movement of moths and flames for their random walk. Both mechanisms emphasize convergence and exploitation proportional to maximum number of generation (iteration). Since this complex task might degrade its performance compare to without limitation or free movement should be a concern. However, the numerical results express that NSGWO algorithm has a little effect of slow convergence at all.
NSMFO algorithm has an advantage of high coverage, which is the result of the selection of position of moth and flame and archive selection procedure. All the position is updated according to their fitness value that enable the algorithm to direct the search space in right direction to find the best solution without trapped in local solution. Archive selection criteria follow all the rules of the entrance and exhaust of any value in it for each iteration and updated when its size full. Solutions of higher fitness in archive have higher probability to thrown away first to improve the coverage of the pareto optimal front obtained during the optimization process.
Conclusion
In this paper the non-dominated MFO multi-objective version of recently proposed moth flame optimizer (MFO) algorithm is proposed known as NSMFO algorithm. This paper also utilizes the transverse orientation strategy for exploration purpose used in its parent MFO version. NSMFO algorithm is developed with equipping MFO with crowding distance criterion, an archive and moth-flame position (accordance to ranking) selection method based on Pareto optimal dominance nature. The NSMFO algorithm is first applied on 17 standard test functions (including eight unconstraint, five constraints and four engineering design problem) to prove its capability in terms of qualities and quantities showing numerical as well as convergence and coverage of pareto optimal front with respect to true pareto front. Then after NSMFO algorithm is applied to real world complex ECEDWP problem where algorithm proves its dominance over other well recognized contemporary algorithms. The numeric results are stored and represented in performance indices: GD, metric of diversity, metric of spacing and computational time. The qualitative results are reported as convergence and coverage in best pareto optimal front found in 15 independent runs. To check effectiveness of proposed version of algorithm the results are verified with SMODE, MOSOS, MOCBO, MOPSO, NSGA-II and other well recognize algorithms in the field of multi-objective algorithms. We can also conclude from the standard test functions results that NSMFO algorithm is able to find Pareto optimal front of any kind of shape. Finally, the result of complex real world ECEDWP problem validates that NSMFO algorithm is capable of solving any kind of non-linear and complex problem with many constraint and unknown search space. Therefore, we conclude that proposed non-dominated version of MFO algorithm has various merits among the contemporary multi-objective algorithms as well as provides an alternative for solving multi or many objective problems.
For future works, it is suggested to test NSMFO algorithm on other real world complex problems. Also, it is worth to investigate and find the best constrained handling technique for this algorithm (Appendix) [48-50].
References
- Kelley CT (1999)Detection and Remediation of Stagnation in the Nelder--Mead Algorithm Using a Sufficient Decrease Condition, SIAM Journal on Optimization 10(1): 43-55.
- Vogl TP, Mangis J, Rigler A, Zink W, Alkon D(1988) Accelerating the convergence of the back-propagation method, Biological cybernetics59(4-5): 257-263.
- Mirjalili S, Mohammad MS, Lewis A(2014) Grey Wolf Optimizer, Advances in Engineering Software, 69: 41-61.
- Xin-She Yang (2010) The bat algorithm (BA), A Bio-inspired algorithm.
- Kennedy J, Eberhart R(1995) Particle swarm optimization, in: Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia.
- Dorigo M, Birattari M, Stutzle T (2006) Ant colony optimization. IEEE ComputIntell Mag 1(4):28-39
- John H Holland(1992) adaptation in natural and artificial systems. MIT Press, Cambridge, UK.
- Gandomi AH, Yang XS, Alavi AH (2013) Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. EngComput 29(1):17-35.
- Sadollah A, Bahreininejad A, Eskandar H, Hamdi M (2013) Mine blast algorithm: a new population based algorithm for solving constrained engineering optimization problems. Appl Soft Comput 13(5):2592- 2612.
- GandomiAH, AlaviAH, Herd K (2012)A new bio-inspired optimization algorithm, Common Nonlinear Sci. Numer. Simul. 17(12): 4831-4845.
- Gandomi AH (2014) Interior Search Algorithm (ISA): A Novel Approach for Global Optimization. ISA Trans 53(4): 1168-1183.
- Beyer HG,SendhoffB (2007) Robust optimization-a comprehensive survey, Computer methods in applied mechanics and engineering 196: 3190-3218.
- KnowlesJD, WatsonRA, CorneDW (2001) Reducing local optima in single-objective problems by multi-objectivization, in Evolutionary multi-criterion optimization, pp. 269-283.
- Deb K, Goldberg DE (1993) Analyzing deception in trap functions, Foundations of genetic algorithms2: 93-108.
- Coello CAC (2002) Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: a survey of the state of the art, Computer methods in applied mechanics and engineering191(11-12): 1245-1287.
- WolpertDH, Macready WG (1997) No free lunch theorems for optimization, Evolutionary Computation, IEEE Transactions on1(1): 67-82.
- Mirjalili S (2015) Moth-flame optimization algorithm: A novel natureinspired heuristic paradigm, Knowledge-Based System89: 228-249.
- Panda,PaniS (2015)Multiobjective colliding bodies optimization, in:Proceedings of 5th Int. Conf. on Soft Computing for Problem Solving, SocProS,IIT Roorkee, India.
- Coello CA, PulidoGT, LechugaMS (2004) Handling multiple objectives withparticle swarm optimization, IEEE Trans. Evol. Comput 8(3):pp.256-279.
- CoelloCoelloCA, LechugaMS (2002) MOPSO: a proposal for multiple objectiveparticle swarm optimization, in: Proceedings of the IEEE Congress onEvolutionary Computation, USA, pp. 1051-1056.
- DebK, AgrawalS, PratapA, MeyarivanT (2000) A fast elitist nondominated sorting genetic algorithm for multi-objective optimization: NSGA-II, in Parallel problem solving from nature PPSN VI pp. 849-858.
- DebK, GoelT (2001) Controlled elitist non-dominated sorting genetic algorithms for better convergence, in Evolutionary multi-criterion optimization pp. 67-81.
- Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II, Evolutionary Computation, IEEE 6(2): 182-197.
- Deb K, Pratap A, Agarwal S, Meyarivan TAMT (2002) A fast and elitistmultiobjective genetic algorithm: NSGA-II, IEEE Trans. Evol. Comput 6(2): 182-197.
- Panda A, Pani S (2016) A Symbiotic Organisms Search algorithm with adaptive penaltyfunction to solve multi-objective constrained optimization problems, Applied Soft Computing 46: 344-360.
- Ngatchou P, Zarei A, El-SharkawiM (2005) Pareto multi objective optimization, in Intelligent Systems Application to Power Systems, Proceedings of the 13th International Conference, USA.
- ParetoV (1964)Coursd’economie politique: LibrairieDroz.
- EdgeworthFY (1881) Mathematical Physics: P. Keagan, London, England.
- Mirjalili S, Saremi S, Mirjalili SM, CoelhoLdS (2016) Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization, Expert Systems with Applications 47: 106-119.
- Yang XS (2011) Bat algorithm for multi-objective optimisation, International Journal of Bio-Inspired Computation 3(5):267-274.
- Akbari R, Hedayatzadeh R, Ziarati K, Hassanizadeh B (2012) A multiobjective artificial bee colony algorithm, Swarm and Evolutionary Computation 2: 39-52.
- Knowles JD, Corne DW(2000) Approximating the nondominated front using the Pareto archived evolution strategy. EvolComput 8(2): 149- 172.
- AbbassHA, SarkerR, NewtonC (2001) PDE: a Pareto-frontier differential evolution approach for multi-objective optimization problems, in Evolutionary Computation, Proceedings of the Congress, South Korea.
- Zhang Q, Li H (2007) MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition, IEEE transactions on evolutionary computation 11(6).
- Zitzler E (1999) Evolutionary algorithms for multiobjective optimization: Methods and applications 63: Citeseer.
- Zitzler E, Thiele L(1999) Multiobjective evolutionary algorithms: A comparative case study and the strength pareto approach, Evolutionary Computation, IEEE Transactions 3: 257-271.
- Sadollah A, Eskandar H, Bahreininejad A, Kim JH (2014) Water cycle algorithm for solving multi-objective optimization problems, Soft Comput 19(9): 2587-2603.
- Sadollaha A, Eskandarb H, Kim JH (2015) Water cycle algorithm for solving constrained multi-objectiveoptimization problems, Applied Soft Computing 27(c): 279-298.
- Veldhuizen DAV, Lamont GB (1998) Multiobjective evolutionary algorithm research: A history and analysis, Citeseer.
- Schott JR (1995) Fault Tolerant Design Using Single and Multicriteria Genetic Algorithm Optimization, DTIC Document.
- Coello CAC (2000) Use of a self-adaptive penalty approach for engineering optimization problems, Computers in Industry, 41(2): 113-127.
- Coello CC, Pulido GT (2005) Multiobjective structural optimization using a microgenetic algorithm, Structural and Multidisciplinary Optimization30(5): 388-403
- Kurpati, Azarm S, Wu J (2002) Constraint handling improvements for multiobjective genetic algorithms, Structural and Multidisciplinary Optimization23(3): 204-213.
- Ray T, Liew KM (2002) A swarm metaphor for multiobjective design optimization, Engineering optimization 34(2): 141-153.
- Qu BY, Liang JJ, Zhu YS, Wang ZY, Suganthan PN (2016) Economic emission dispatch problems with stochastic wind power using summation based multi-objective evolutionary algorithm, Information Sciences 351: 48-66.
- Hota PK, Barisal AK, Chakrabarti R (2010) Economic emission load dispatch through fuzzy based bacterial foraging algorithm, Electr. Power Energy Syst 32(7): 794-803.
- AbidoMA (2003) Environmental/economic power dispatch using multiobjective evolutionary algorithms: a comparative study, IEEE Trans Power Syst 18(4): 1529-1537.
- BinhTT, KornU (1997) MOBES: A multiobjective evolution strategy for constrained optimization problems, in The Third International Conference on Genetic Algorithms (Mendel 97).
- Osyczka, Kundu S (1995) A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm, Structural optimization10(2): 94-99.
- Srinivasan, Deb K (1994) Multi-objective function optimisation using non-dominated sorting genetic algorithm, Evolutionary Comp 2(3): 221-248.
- Zhu YS, Wang J (2014) Multi-objective economic emission dispatch considering wind power using evolutionary algorithm based on decomposition, Electr. Power Energy Syst 63: 434-445.






























