The Effect of Bio-Fuel Induced Bsfc Curve Perturbations on Realizable ICE Efficiency Using Cycling
Peter Bauer1* and Jenny Murillo2
1Department of Electrical Engineering, University of Notre Dame, Spain
2Department of Engineering, Rovira i Virgili University, Spain
Submission: March 01, 2018; Published: May 24, 2018
*Corresponding author: Peter Bauer, Department of Electrical Engineering, University of Notre Dame, Avda. Països Catalans, 26, 43007, Tarragona, Spain, Tel: 574-631-8015, Email: peter.h.bauer.2@nd.edu
How to cite this article: Peter B,Jenny M. The Effect of Bio-Fuel Induced Bsfc Curve Perturbations on Realizable ICE Efficiency Using Cycling. Eng Technol Open Acc. 2018; 1(5): 555573. 10.19080/ETOAJ.2018.01.555573
Abstract
This paper provides an uncertainty analysis for efficiency gains in internal combustion engines generated by cycling between two operating points. The uncertainties are due to incomplete knowledge of the bsfc field of the engine. In the case of bio fuels, these uncertainties can be fairly large and exact bsfc curves are rarely available. The proposed concept provides a graphical method for determining whether cycling provides efficiency advantages despite the presence of uncertainties. If cycling is beneficial for efficiency, the introduced concept provides the power range those results in efficiency advantages. The proposed method is based on a graphical evaluation in the engine bsfc field, with uncertainties being represented by a bsfc envelope. The decision making criterion is based on the bsfc envelope and its relationship to the cycling induced bsfc curve.
Keywords: BSFC; Efficiency; Bio-fuel; Cycling; ICE
Highlights
a. An envelope based model for bsfc uncertainties was introduced.
b. A method for determining if cycling provides efficiency benefits under bsfc uncertainties was introduced and graphically illustrated.
c. The effects of bsfc uncertainties on the power band for achievable bsfc gains was analyzed
Nomenclature
Bsfc [g/kW⋅h]Brake Specific Fuel Consumption
ICE [u]Internal combustion engine
CNG [u]Compressed natural gas
α1 [0-1] Duty cycle coefficient for power P1
α2 [0-1] Duty cycle coefficient for power P2
Δbsfc(p) [g/kW⋅h] The difference between bsfc for Diesel and Bio-Diesel as function of brake power
P [ kW] Engine brake power
P1 [kW] Power of low power operating point for Diesel
optP [kW] Brake power for which the bsfc minimum is reached for Diesel
avgP [kW] Average power
bsfcp [g/kW ⋅h] Mapping from P
bsfcp [g/kW ⋅h] Upper bsfc envelope boundary
bsfcp [g/kW ⋅h] Lower bsfc envelope boundary
ibsfcp [g/kW ⋅h] Induced bsfc using cycling between
bsfcP, ()optbsfcP.
Pmin [kW]Minimum power of power band for cycling
Pmax [kW]Maximum power of power band for cycling
S [%]The minimal percentage savings
Introduction
The choice of engine operating points is of great importance for the design of fuel efficient hybrid drive systems [1-9]. Since in hybrid drives, generated power can be chosen more and less independent of load power, the choice of operating points of the engine is much less restricted. In essence, operating points that correspond to low efficiency or high brake specific fuel consumption need to be avoided and operating points at or near the lowest bsfc region should be utilized.
In order to make a compelling case for the use of hybrid power train technology in large heavy duty vehicles, one needs to show the efficiency advantages over conventional drive systems. While this has been done for a number of scenarios in previous work [1,10], the assumption in previous work was always the exact knowledge of the bsfc field. There are however a variety of influences, environmental or otherwise, that can change the bsfc field significantly. Some of these factors are engine and air temperature, atmospheric pressure and altitude, humidity as well as fuel additives such as Bio-Diesel and other types of air or fuel mixtures. Very often, the bsfc field is not completely known and only a few points in the entire bsfc diagram have a known bsfc value. Therefore, this paper introduces an uncertainty analysis on bsfc curves of ICEs with the goal of determining the benefits of cycling under bsfc field perturbations. The term “cycling” denotes engine operation at a few (here: two) operating points only. It has been shown previously [1], that especially selecting operating points can generate significant efficiency advantages for some engines [2-9]. This is especially true if the engine was designed for cycling, but conventional engines can also show efficiency gains from cycling [10]. The highest efficiency gains obtainable from cycling between two operating points are most often generated if one operating point is the global bsfc minimum and the other is close to zero power [1]. Previous work has addressed the problem of achievable efficiency gains through cycling for bio-fuels [11], albeit under the assumption of exactly known bsfc dependencies for both, regular Diesel and Bio-Diesel. Conditions under which the efficiency advantages of cycling for regular Diesel carry over to the case of Bio-Diesel were formulated.
This article examines how despite the presence of bsfc uncertainties one may still be able to decide whether engine cycling provides overall efficiency benefits. The results are especially applicable to bsfc uncertainties introduced through a variety of fuel mixtures such as Diesel and Bio-Diesel, Diesel and hydrogen, Diesel and CNG, and other environmentally preferable fuel additives that affect the bsfc field of an engine.
Previous Work and Objective
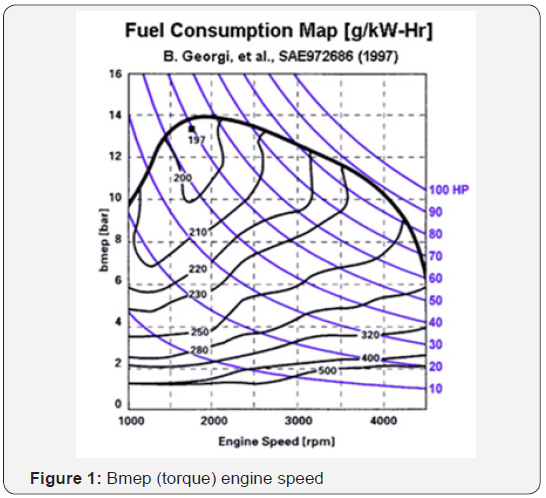
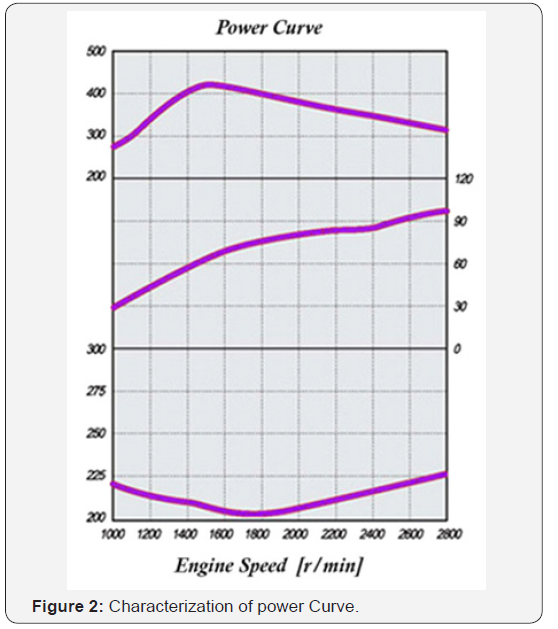
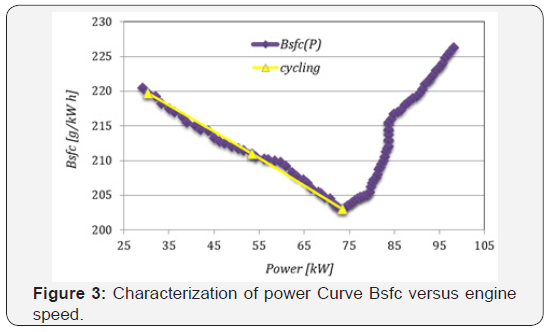
The bsfc data for engines is often provided in the torque versus engine speed or power versus engine speed diagram (Figure 1). Alternatively separate characterization of bsfc and power or torque under full load are also often used (Figure 2). It is obvious that given a power P, there are, except for some degenerate cases, infinitely many different bsfc values associated with this power level P. Therefore we define the function bsfc( p) as a mapping from P to the lowest possible bsfc at power P, essentially converting the usual relation bsfc( p) to the function bsfc( p) (Figure 3).
The here introduced concept builds on the work in Bauer PH et al. [11] where for the first time, an analysis was carried out that showed the conditions under which operating point switching provides efficiency advantages in Bio-Diesel fuelled engines, given the complete knowledge of the bsfc field for regular Diesel and Bio-Diesel In a method to gauge fuel efficiency of cycled ICEs with two operating points was introduced [1]. The results in Bauer PH et al. & Ehsani M et al. [11,12] show how one can use bsfc results on cycling for regular Diesel fuel and extrapolate to Bio-Diesel. The results were based on the difference between the regular Diesel bsfc curve and the relationship to Bio-Diesel in conjunction with a number of simplifying assumptions. In particular it was shown, that if the difference between the regular Diesel and Bio-Diesel bsfc curves is approximately constant, and then the efficiency benefits of cycling carry over from regular Diesel to Bio-Diesel. Another case for which the benefits of cycling carry over to Bio-Diesel are bsfc curves where the difference between the two respective bsfc curves is maximal at the end points, i.e. the two operating points. The exact condition was given as:
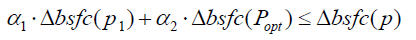
Where,
P1 ≤ P ≤ Popt α1 +α2
The objective of this paper is to present a method for determining efficiency gains based on ICE cycling between two operating point, if the bsfc curve is not exactly known. More specifically, we assume the bsfc curve uncertainty is due to a bio-fuel mixture for which exact bsfc data is often not available.
Methods
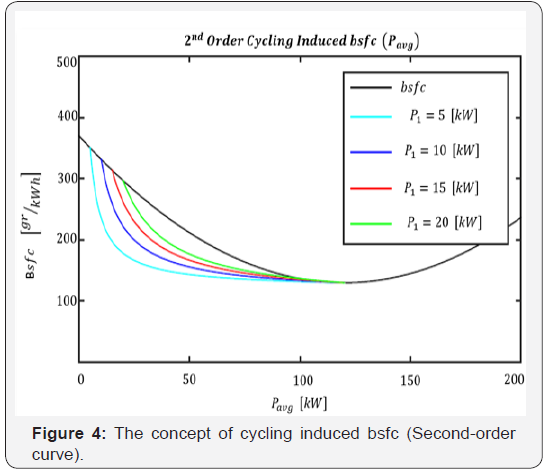
The approach taken for analysing the benefits of cycling under bsfc uncertainties are based on the concept of “cycling induced bsfc”, a concept that was introduced by the authors in Campanaro J et al. [1]. The relationship between the bsfc curve and the cycling induced bsfc curve are shown in Figure 4. The figure shows cycling bsfc for two different bsfc curves represented by a second and forth order polynomial respectively. If the cycling induced bsfc curve is below the regular nominal bsfc curve, cycling creates an efficiency advantage. The cycling induced bsfc can be expressed as follows:
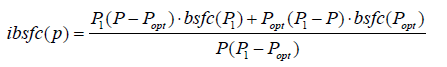
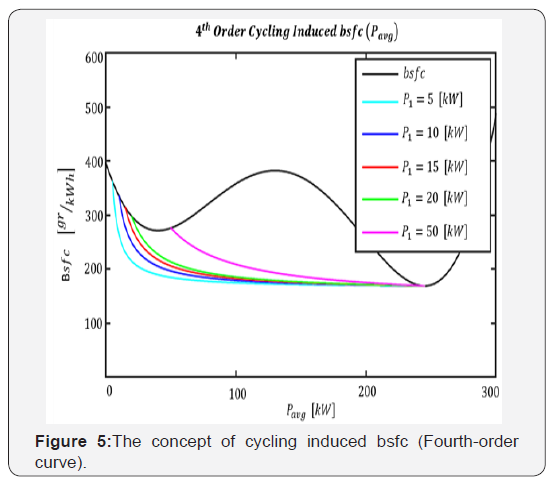
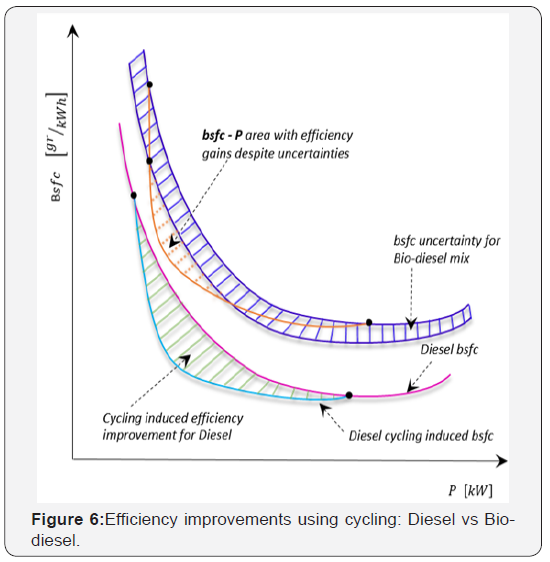
Using knowledge of the nominal bsfc curve, sparse measurement data or extrapolations, we construct bsfc intervals for every power level thus creating an envelope around the nominal curve. This envelope then contains the real bsfc curve and the upper and lower envelope boundary can be taken as the worst and best case bsfc respectively. The relationship between cycling induced bsfc and regular nominal bsfc under bsfc uncertainties for bio-fuel mixtures and exactly known bsfc for Diesel is shown in Figure 5. The two lower curves show the bsfc for regular Diesel and the cycling induced bsfc for this case. It is easily seen that the cycling induced bsfc curve falls below the Diesel bsfc curve for a wide power range. In other words cycling is beneficial over a wide power range. The upper three curves in Figure 4 represent the upper and lower envelop boundary for the uncertain Bio-Diesel bsfc and the corresponding worst case cycling induced bsfc. The power range for which the cycling induced bsfc is below the envelope of the Bio-Diesel bsfc is comparatively small and the gains in that range are also rather limited. Therefore this mechanism provides a fairly simple graphical method to check whether the cycling induced bsfc is below the conventional bsfc curve and provides the power range for which cycling under uncertainties or perturbations remains advantageous. Figure 6 shows the case of bsfc curves created from two different levels of bsfc uncertainties. It is apparent that an increase in bsfc uncertainty reduces the size of the power interval for which cycling produces efficiency advantage. Similar approaches can be taken to handle the case of uncertainties created by environmental effects such as engine temperature, air pressure and humidity, etc.
Analytically the graphical method can be expressed as follows:
Cycling under bsfc uncertainties is beneficial if for power P we have:
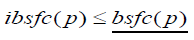
The boundaries of the power interval for which cycling is advantageous is given by the two solutions of the equation:
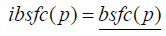
If this equation has no solution then cycling under uncertainties does not provide efficiency advantages for any power level. While this is not shown in Figures 4 & 5, theoretically there can be more than two solutions to the above equation. However in reality this case almost never occurs for highly loaded conditions. So from here on we assume there are only two solutions to this equation, which we denote as Pmin and Pmax , with min max Pmin ≠ Pmax . Let us now consider the case where power is produced within this interval, i.e. Pavg ∈ [Pmin,Pmax] .
Then the minimal percentage savings S relative to the conventional case of operating the engine at power level avg P is given by:
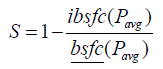
In a similar way one can construct an expression for the maximum percentage savings. In this case the lower bsfc envelope needs to be considered for the construction of ibsfc via power levels P1 and Popt and the maximum envelope needs to be utilized for avg P .
Conclusion
This paper introduced a graphical method to determine whether engine cycling results in efficiency benefits for a variety of bio-fuels under a multitude of different operating conditions. The method is based on the concept of cycling induced bsfc and provides the interval of power levels that lead to improved efficiency. The proposed concept can effectively deal with uncertainties induced by different fuel mixtures as well as environmental conditions such as engine temperature, ambient air pressure, humidity, etc. Coarsely sampled bsfc fields with large uncertainties can also be analysed using the proposed approach. The results are an improvement over existing methods which typically assume exact knowledge of the bsfc relationships for both, regular Diesel and Bio-Diesel.
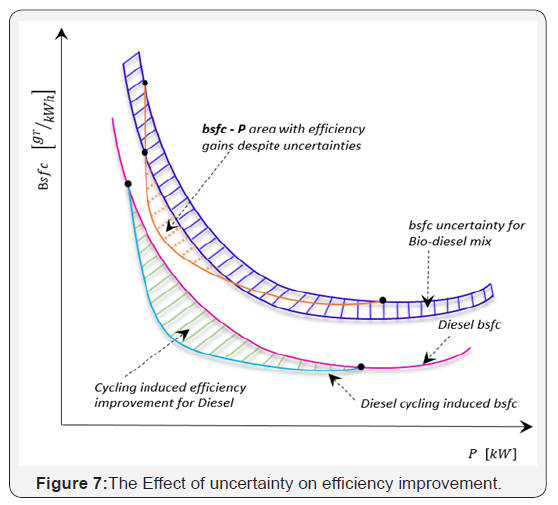
Future work concentrates on improving the conservativeness of the results. It can be seen from Figure 7, that our method essentially is a worst case analysis, since we assume the highest possible bsfc at the two operating (end) points and the lowest bsfc in between these two operating point. For very large uncertainties in the bsfc values, the introduced method provides only very small power ranges for which cycling generates efficiency advantages. In extreme cases, it may not provide any solution. Therefore one may improve over the results provided in this article by an approach that uses families of bsfc curves in parameterized form that makes use of the fact that the bsfc curves are smooth curves without discontinuities.
Acknowledgement
This work was supported by NSF grant No 1239224. We gratefully acknowledge the financial support of NSF.
References
- Campanaro J, Ruof M, BauerM, Murillo J (2016) Optimizing ICE Efficiency through Cycling: Methods for Evaluating Achievable Gains, Canada.
- Paganelli G, Tateno M, Brahma A (2001) Control development for a hybrid-electric sport-utility vehicle: strategy, implementation and field test results. American Control Conference. Arlington, USA.
- Musardo C, Rizzoni G, Guezennec Y (2006) An adaptive algorithm for hybrid electric vehicle energy management. International Mechanical Engineering Congress and Exposition. Chicago, Illinois, USA.
- Pisu P, Rizzoni G (2009) A Comparative Study of Supervisory Control Strategies for a Series Hybrid Electric Vehicle. Power and Energy Engineering Conference, Wuhan, China.
- Salmasi FR (2007) Transactions on vehicular technology, Control strategies for hybrid electric vehicles: Evolution, classification, comparison, and future trends. IEEE Transactions on Vehicular Technology 56(5): 2393-2404.
- Baumann BM, Washington G, Glenn BC, Rizzoni G (2000) Mechatronic design and control of hybrid electric vehicles. IEEE Transactions on Mechatronics 5(1): 58-72.
- Emadi K, Rajashekara, Williamson SS, Lucik SM (2005) Topological overview of hybrid electric and fuel cell vehicular power system architectures and configurations. IEEE Transactions on Vehicular Technology 54(3): 763-770.
- Bayindir KC, Gözüküçük MA, Teke A (2011) A comprehensive overview of hybrid electric vehicle: Powertrain configurations, powertrain control techniques and electronic control units. Energy Conversion and Management 52(2): 1305-1313.
- Schouten NJ, Salman MA, Kheir NA (2003) Energy management strategies for parallel hybrid vehicles using fuzzy logic. Control Engineering Practice 11(2): 171-177.
- Bauer PH, Murillo J (2015) An Analysis of Conditions for Efficiency Gains in Large ICEs Using Cycling. ICHEV, Istanbul.
- Bauer PH, Murillo J (2016) Biodiesel versus Diesel: A Comparative Analysis of the Effect of Engine. World Bio Diesel Congress & Expo. San Antonio, USA.
- Ehsani M, Gao Y, Emadi A, Gay S (2005) Modern Electric, Hybrid Electric, and Fuel Cell Vehicles, CRC Press.






























