Research article

Altitudes Effects in Calibration of Ground Doppler Radar for Rainfall Estimation

Ali Nikahd*

Department of Geoinformatics and Real Estate, University of Technology, Malaysia

Submission: February 19, 2018; Published: May 17, 2018

*Corresponding author: Ali Nikahd, Department of Geoinformatics and Real Estate, College of Geoscience & Digital Earth Centre (INSTeG), University of Technology, Malaysia, Email: ali.nikahd@yahoo.com

How to cite this article: Ali Nikahd. Altitudes Effects in Calibration of Ground Doppler Radar for Rainfall Estimation. Eng Technol Open Acc. 2018; 1(5): 555571. 10.19080/ETOAJ.2018.01.555571

Abstract

Unipolar ground-based weather radar has been a widely-used instrument for rainfall measurement. These radar measurements however need to be calibrated for more accurate rainfall estimation. This article introduces a new calibration approach using time-stepwise processing of reflectivity-rainfall rate (Z-R) relationship. Based on previous work utilizing the radar-rainfall relationship; this article hypothesizes that the rainfall measurement from ground based radar are affected by distance from radar, altitudes and rainfall time duration. Two consecutive years unipolar ground-based radar data sets with 77 occurrences of rainfall from 39 stations in calibration window of three hours; and the corresponding rainfall measured from registered rain gauges were used in this study. The results indicated that radar-rainfall relationship Z=aRb is better improvise with altitudes effect (H) and empirical coefficient (c), such that (Z=aRbHc). The changes in ‘distance from the radar’ and ‘duration of precipitation’ were evidently significant. For radar-rainfall relationship individually (R2=min88, max97) with altitude effect (H) in relationship (R2=min70, max97). It is therefore concluded that the use of other effective parameters (distance from radar, altitudes and rainfall time duration) leads to optimum accuracy of Z-R relationship.

Keywords: Radar-rainfall; Relationship; Calibration; Altitudes

Abbrevations: RHI: Range Height Indicator; PPI: Plan Position Indicator; CAPPI: Constant Altitude Plan Position Indicator; IMO: Iran Meteorological Organization; dB: Decibel

Introduction

RHI: Range Height Indicator; PPI: Plan Position Indicator; CAPPI: Constant Altitude Plan Position Indicator; IMO: Iran Meteorological Organization; dB: Decibel

In this paper, we investigate the effects and properties of the altitude and rainfall time duration in radar-rain gauges relationship in order to ground-based radar calibration. Since 1948, after Second World War, weather ground-based radars are predicting rainfalls based on Marshal-palmer proposed relationship [6]. According to this universal relationship, there is a strong correlation between the rate of the radar reflectivity (Z) (dB) and the rainfall amount (R) (mm/h) that is known the Z-R relationship. Return signal from atmosphere targets are dimensionless information and called dimensionless radar output (DRO). The DRO value is the 8bit alteration of audio-visual motion that ranges between 0-255 dimension integers [3]. However, there are a strong relationship between Z and R in Z=AR^(b ) equation this does not mean that reflectivity from radar is exactly equal to the amount of rainfall [7,8]. The A and b are empirical coefficients which refer to climatological characters, location of rainfall, rainfall seasons, geographic latitudes [9] and rainfall time duration [10]. The empirical coefficients depend on climate characteristic in each area exclusively [11]. A lot of researches have been done to determinate Z-R relationships and relevant regional coefficient [12]. More than 100 relationships are available for different rainfall form such as strait form, tropical, convective, thunderstorm, shower, monsoon and hurricanes [7]. The sensitivity variation of Z–R relationships are the main uncertainty sources [13], especially in rainfall calculation based on DSD. Because of radar measurements carry many uncertainty sources depending on dissimilarities of radar reflectivity in the atmosphere; Radar calibration is unavoidable to estimate the amount of rainfall precisely [14]. Consequently the values of A and b coefficient is fluctuating from place to place, season-to-season, and time to time.

As, most of the improbability occur more far from the radar, distance from the radar is a main factor in all of uncertainty sources [15]. Most errors are found away from the radar [16]. This means that majority uncertainty is related to dimension from the radar [17]. Distance (d) between overshooting reflectivity (radar station) and the location of drop raining (DSD) is very important parameters to ground-based radar calibration. Previous studies have shown that this calibration can further improved radar-rainfall estimation by use of multiple Z-R relationship [18], rainfall types [19], distance from the radar [20] and other parameters [21]. These parameters are discussable in different weather situation in all rain’s types at duration of different seasons.

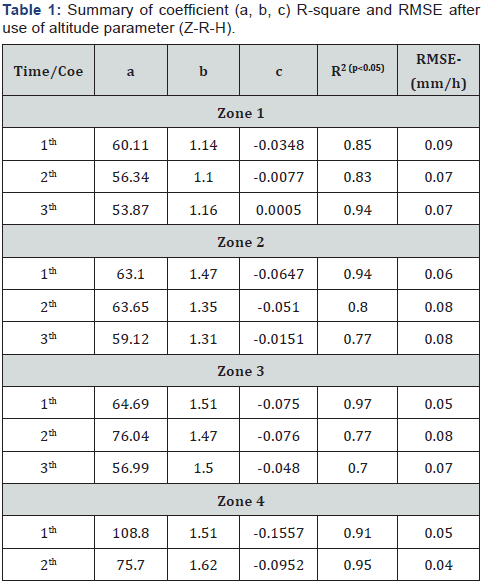
In addition to the above calibration, this study also hypothesize a new improvement of the universal relationship taking in to account the effects of altitude (H) and distance from radar (D) and other new coefficient such as (c). Thus producing new improve algorithm for the relationship such that Z=AR^(b) H^(c). The radar zones are defined in circular shape from the center of radar station. The effects of distance in rainfall estimation are investigated in 0-50km (zone 1), 50-100km (zone 2), 100-150km (zone 3) and 150-200km (zone 4) far from the radar. Also this paper uses the hourly rainfall products from registered rain gauges.

Radar Rainfall-Relationship

It is assumed that raindrop shapes are spherical and sizes are smaller than the radar wavelength. There are special equations between reflectivity and the characteristics of rain drops. It is important to qualify radar reflectivity (Z) because the reflectivity depends on the number and diameter of raindrops on the radar sample volume [22]. The reflectivity (Z) is dependent of number, diameter and velocity of rain drops;

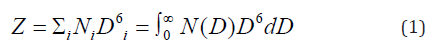
And

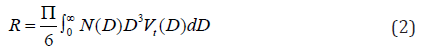
Where Z(mm6 / m3 ) is reflectivity, R(mm / h) is the rainfall rate, N (D)dD is the mean sum of raindrops, D(dD)(mm) / m3 of air (Ni is the number of drops with Di the diameter of the ith element), and Vt (cm/second) is the droplet terminal velocity. If the above equation (1,2) with respect to the similarity parameters equivalent to each other, the equation (3) will be;

This means there are strong relationships between reflectivity and the amount of rainfall. According to this strong relationship, the A and b coefficient has been found consequence of improve the equation (3);

It is assumed that height differences (altitude) are more effective parameter in radar-rainfall estimation.

Here this paper tries to improve equation (4) and corroborate equation (5).

Unipolar Ground Based Radar

Unipolar ground based radar in Ahvaz, Iran (latitude: 31˚20’, longitude: 48˚40’ and 152m height) is use in this study. Figure 1 shows the location and configuration of Ahvaz’s radar station with the zones of data acquisition. The area of coverage by this radar footprint is between 29˚55’ until 32˚30’ in semi-arid zone at northern hemisphere. Ahvaz is a S-band radar which is located close the Ahvaz city in 31˚20’N with 7.5cm wavelength and 2GHZ that is serviced by 750 kilowatt transmitter power. The radar transmitter is of TXS 1500 model that includes a modulator with an active klystron tube-produce and amplifies microwave pulse. The antenna diameter and Radom diameters are 8.5m and 11.65m, respectively. The Doppler range is 200km and non- Doppler range is 400km; spatial resolution is 1x1km. Details about technical specifications are shown in Table 1. The station has the capability of producing the range height indicator (RHI), plan position indicator (PPI), constant altitude plan position indicator (CAPPI) and SRI.

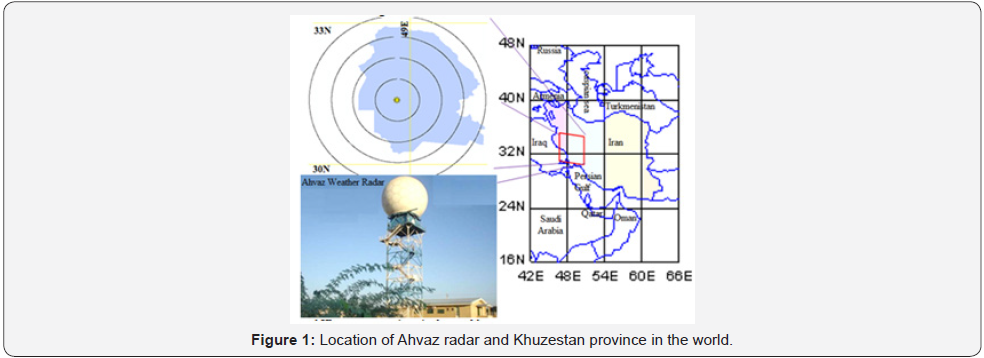
This study, however, only used plan position indicator (PPI). The entire Ahvaz radar station is managed by Iran Meteorological Organization (IMO) and is under the jurisdiction of national weather radar network. The main radar data acquire reflectivity numerical amount per decibel (dB) unit. These data are processed using the RAINBOW software to convert radar reflectivity into dB unit. The rainfalls are typically in reflectivity range between 5-75dB; light rain begins at 5dB and hails at 80. To investigate changes due to different distances between reflectivity and rainfall location data were recorded from four zones surrounding the radar station (Figure 1).

Algorithm Process

The basic background of this theory for this study is that, for each altitude can estimate one Z-R relationship. Also Z-R relationship changes are considerable in each step time of rainfall time duration. Accordingly, it is designed two algorithms based on multiple regressions. In first step, the algorithm starts whit simple mode; relationship between one independent variable and one dependent variable. Rainfall (mm/h) in all equation is independent variable and radar reflectivity (dB) is dependent variable. Variable is arranged based time hourly. According to the general relationship (marshal- palmer), the equation is;

This relationship is extended for all station that is collection in 3 three hours of rainfall and four zones surrounding radar.

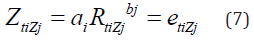
Where, Z is radar reflectivity, R is rainfall amount, ti is rainfall time duration, 1th-2th-3th hours of rainfall; here is investigated 3 time of rainfall from rainfall start until 3th time of rainfall based hourly. The j Z introduce four zones; zone1 (0-50km), zone2 (50-100km), zone3 (100-150km), zone4 (150-200km). The coefficient i a and i b are the empirical coefficients and tiZj e are partial errors in each zone and each time. Taking into account, all of the data in a coordinate system, we can to reach equation (8);

The (t) is mean; using all data in the entire region of rainfall in one coordinates.

Second algorithm tries to find new matrix mode of data with effects of altitude differences. This parameter for first time is used in this paper. When the factor H is considered in the second algorithm, the coefficient (c) is generated. (c) Coefficient is a novel empirical coefficient that is dependent of geomorphology rainfall location. Here after, (c) coefficient is called “altitude coefficient”. The new algorithm is introduced in equation (9); such that;

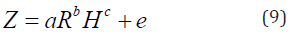
This algorithm is experimented in 3 hours of rainfall occurrences in 4 defined zones center about Ahvaz radar station.

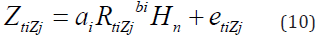
Equation (10) parameters are exactly same equation (7), the only difference is n H . The n H show altitude changes at each point where the rainfall is measured. Taking into account, all of the data in a coordinate system, t; is the total of data. As a result, we can to reach equation (11);

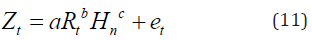
As a result, equation (11) presents the relationship between reflectivity and all parameters and coefficients in all data in all places and all times of precipitation. However, previous studies have determined the relationship between reflectivity and rainfall amount based on power regression [3,4,10,13,18,23- 28]. But, it is possible that the relationship be manifested in other matrix form such as; linear, logarithmic or exponential regression. Here, according to Marshall-palmer first used power regression in all parameters of research. In this paper, in order to measure distances and geographic location control is used ArcGIS 9.3 software. It is used 2011b version of MATLAB software to mathematics and technical computing.

Results

There are strong relationship between radar reflectivity and rainfall amount in semi-arid zone in the middle latitudes and relevant coefficient. Z-R relationship is investigated in all zones and 3 time of rainfall time duration (Table 2).

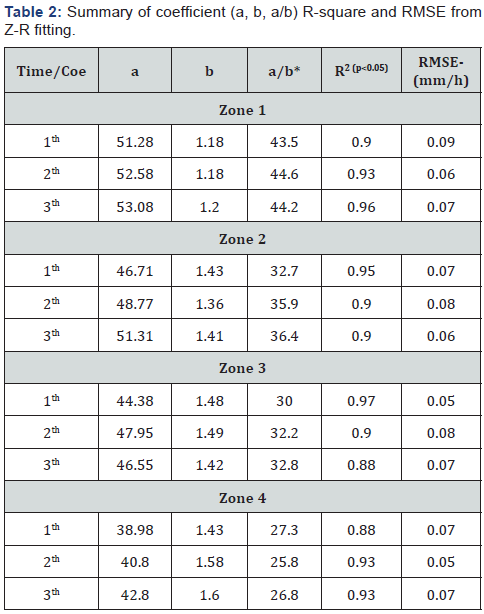
Table 3 shows the amount of empirical coefficient (a, b) and relationship between variables in 4 zones and 3 times of rainfall. There are no significant differences between value obtained and other research in middle geographic latitudes. We found the range of coefficients of variation; (38.98

Exploration the relationship among altitudes (H), radar reflectivity (Z) and rainfall amount (R); Z-R-H

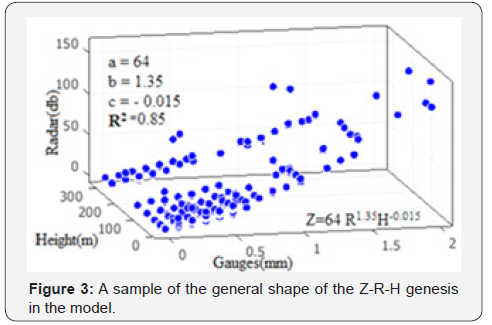
According to equation (11), Z = aRbHc + e has been proven, there are strong relationship between Z-R-H. In the new hypothesized relationship, upon entering H parameter, the c coefficient is generated. The c coefficient changes show the condition and characteristic of altitude parameter. Figure 3 schematically shows the general shape of the Z-R-H genesis, as discussed in this article. The value of this new empirical coefficient is a negative numeric, which infers that reflectivity (Z) with altitude (H) have inversely proportional relationship. Also, at higher elevations, much less radar reflectivity is noted. This can be interpreted based on the convective precipitation at height. The Z-R-H relationship is investigated in all zones and 3 time of rainfall time duration.

Table 3 shows the value of coefficient c with respect to other related parameters in all locations (zones) far from the radar station. We found that coefficient c varies within range of (0.0005) to (- 0.0952), with significant changes in distant zones. It is clearly evident that the amount of reflectivity is less in distant zones. But in terms of the third zone is different due to the mountainous conditions. It can be explained and justified. 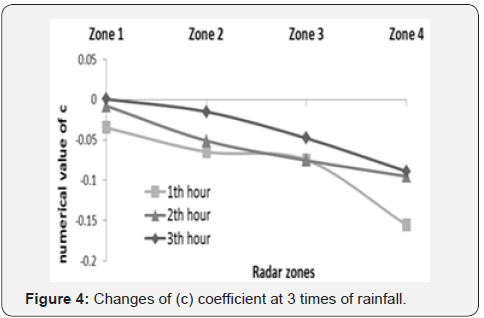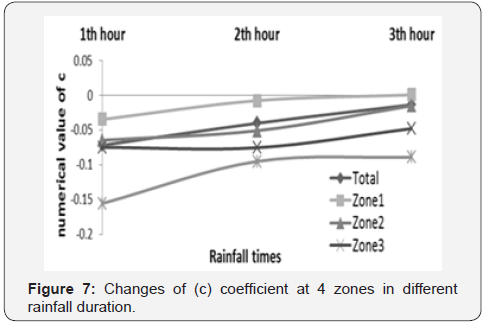This result is not unexpected. Figures 4 & 5 are shown the amount of new empirical coefficient and relationship between 3 variables in 4 zones and 3th times of rainfall.

In summary it can be said; Z-R relationship at different heights, various distances from the radar station, even when rainfall begins moment to end rainfall is very changeable. Based on this theory that others parameters are effective and can be entered in the Z-R equation.

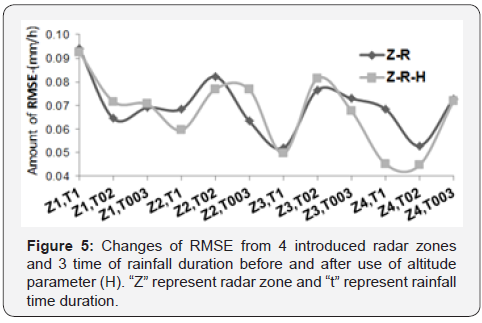
Therefore, the altitude parameter (H) was entered and confirmed through this study. Changes of RMSE, in simple mode (Z-R) and when use altitude parameter (Z-R-H) show that new improved algorithm has better fitting. Figure 5 demonstrate changes of RMSE from 4 introduced radar zones and 3 time of rainfall duration before and after use of altitude parameter (H). 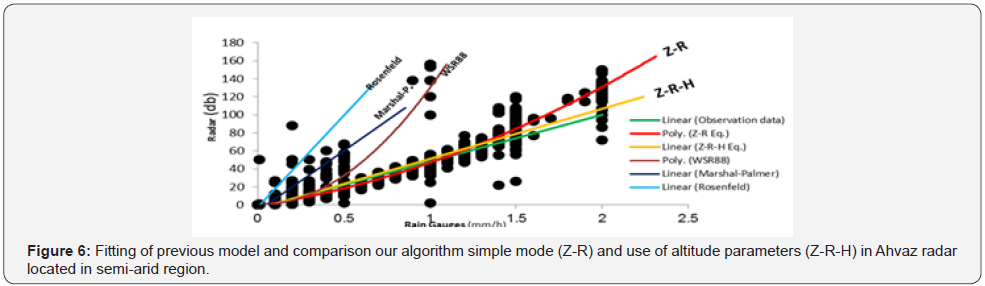Amount of RMSE in new mode (Z-R-H) at 4 zones of radar and 3 times of rainfall is lower than before use of altitude parameter in equation. Figure 6 is fitting the previous equations (Marshall- Palmer, Rosenfeld and WSR 88) and our research with and without altitude parameter. Amount of RMSE confirm that the new Z-R-H equation is able to replace with universal Z-R equation (Table 3).

Discussion

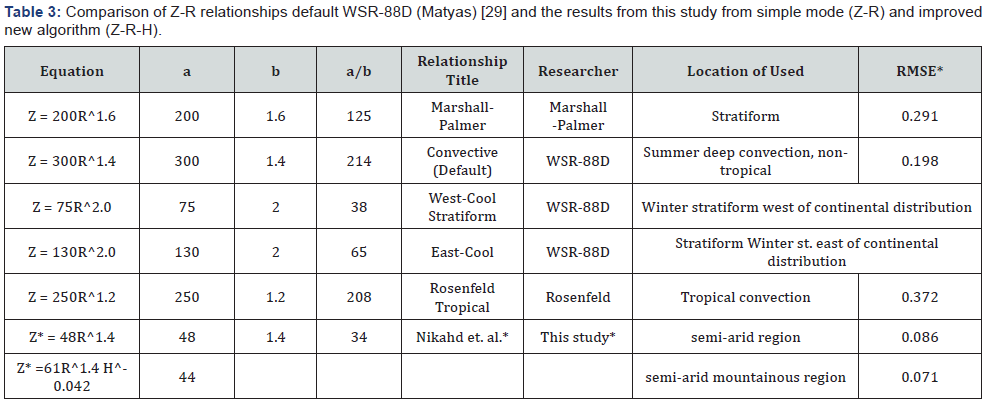
Using the Z-R-H methodology for unipolar ground-based radar calibration and vagueness estimation provides beneficial and valuable outcomes. This equation is applied on the radar calibration, which suit precisely for unipolar ground-based radar type. The results of this study clearly illustrate that the agreement between radar reflectivity and rainfall amount is highly dependent on altitudes effects. Table 3 summarizes the comparison of Z-R relationship obtained with similar previous studies. The value of empirical coefficients from different areas is presented. This study noted Z-R relationship in semi-arid region, where the coefficients are unique. Also, considering that the other parameters have been ignored in radar rainfall estimation, this study has focused on three effective parameters in radar rainfall equation: altitudes effects, distance from radar and rainfall duration.

Accordingly, to investigate the effectiveness of distance from radar, areal coverage was divided into 4 zones. To determine impact of altitudes, altitude for all rain gauges was interfered in the equation. The first three hours of rainfall was considered in order to enable detection of changes in rainfall in initial precipitation and subsequent periods. Such results are commonly used for meteorology and hydrological applications; hence, this is beneficial and particularly important to similar regions of study.

This paper noted strong relationship (R2min=83) between radar reflectivity and the amount of rainfall (Z-R), in the semiarid zone in geographic middle latitude of northern hemisphere. Empirical coefficient (a,b) changes presented relevant correlation in different situation and location far from the radar source. They are strongly dependent. The new a/b coefficient expressed the changes empirical coefficient far from the radar. As it is distant away from the radar station, a/b coefficient decreases, indicating that radar echoes are less returning to receiver from far radar stations. This result is not unexpected, because the uncertainty resources have a large impact on the amount reflectivity. It is evident that all the empirical coefficients do not change with different time of rainfall. Nonetheless, there is no considerable a/b coefficient changes in first to third time of rainfall occurrence. Evidently, there are minor changes, but cannot be fully interpreted at this point time as they do not follow a logical sequence (Figure 4 & 7). The benefit of the a/b is obvious, since the changes of amount of rainfall changes with corresponding radar reflectivity in far from the radar (distance) and duration of rainfall time. Hereafter, in order to allow for very fine radar adjustment it is therefore better to use a/b coefficient instead of (a) and (b) coefficients separately. This fine adjustment is very sensitive in case like calibrating of Z-R relationship for urban areas for flood control that needs more caution. New coefficient a/b has the ability to show characteristic of region better than last empirical coefficients. It can be a strong default for ground based radar in different geographic latitude prior to anticipated operations.

The altitudes parameters entry in radar equation is the first attempt in this study and this is very crucial in this field of study. Given that the others parameters in the Z-R relationship can be effective, altitude (H) parameter is entered and for first time Z-R-H is defined. In the new hypothesized relationship, upon entering H parameter, the coefficient c is generated. The coefficients changes show the condition and characteristic of altitude parameter. Figure 6 shows an overall trend of the Z-R-H, as discussed in this article. Although the case study (Khuzestan province) is a relative flat area and parameter H with coefficient c changes are explainable in different location and times. Figure 6 is fitting the previous equations (Marshall-Palmer, Rosenfeld and WSR 88) and our research with and without altitude parameter. A change in c shows the effect of rainfall types (mountainous and conventional) in radar equation. Maximum value of R-square 98 in different time and different location shows there are strong relationships between 3 parameters, namely, the Z-R-H. The coefficient c changes ranges 0.0005 to-0.0952. We noted c coefficients are negative values, except highest value in the first zone at 3rd times of rainfall. These negative values in power of altitude parameter (H) display that at higher altitudes the return echo (Z) is lower than flat areas, and this is agreeable to amount of precipitation at higher altitudes is more than plain. These results can interpret amount of mountainous precipitation in radar-rainfall equation. An inevitable consequence of the relationship is that the H parameter and c coefficient would be the main part of radar-rainfall equation (Z-R) for future users in hydrometeorology. The ultimate amount of Z-R-H relationship for semi-arid zone is obtained and is given in Table 3.

The results of this study also well indicated that coefficient c alternate from first time of rainfall to other next times. So we can say that, when more time of precipitation passes the value of (c) coefficient is greater. We interpreted this is due to the “increase influence of convective phenomena”. Obviously, the level of this claim is a discussable theory. Notable issue is that, there is no a/b coefficient changes in duration of rainfall times but coefficient c varies considerably. The new relationship is very useful in watershed hydrology management because the duration of precipitation and distance from the location of the precipitation from basin outlet is very important especially in flood routing and flash flood control. Although, the authors have considered the new relationship in order to allow radar calibration, it is not doubtful that any improvement by using other effective parameters will be highly rational.

References

1. Barthès L, Mallet C (2013) Rainfall measurement from the opportunistic use of an Earth-space link in the Ku band, Atmos Meas Tech 6(8): 2181- 2193.
2. Dai Q, Rico-Ramirez M, Han D, Islam T, Liguori S (2014) Probabilistic radar rainfall nowcasts using empirical and theoretical uncertainty models. Hydrol Process 29(1): 66-79
3. Nielsen JE, Beven K, Thorndahl S, Rasmussen MR (2014) GLUE based marine X-band weather radar data calibration and uncertainty estimation. Urban Water J 12(4): 1-12.
4. Nielsen JE, Thorndahl S, Rasmussen MR (2014) A numerical method to generate high temporal resolution precipitation time series by combining weather radar measurements with a nowcast model, Atmos. Res 138: 1-12.
5. Villarini G, Seo B, Serinaldi F, Krajewski WF (2014) Spatial and temporal modeling of radar rainfall uncertainties, Atmos. Res 135-136: 91-101.
6. Atlas D (2004) radar calibration-some simple new approach.
7. Prat O, Barros A (2009) Exploring the Transient Behavior of Z-R Relationships: Implications for Radar Rainfall Estimation 48: 2127- 2143.
8. Mandapaka PV, Krajewski WF, Ciach GJ, Villarini G, Smith JA (2009) Estimation of radar-rainfall error spatial correlation. Adv Water Resour 32(7): 1020-1030.
9. Chumchean S, Seed A, Sharma A (2006) Correcting of real-time radar rainfall bias using a Kalman filtering approach. J Hydrol 317(1-2) 123- 137.
10. Suk MK, Chang KH, Cha JW, Kim KE (2013) Operational Real-Time Adjustment of Radar Rainfall Estimation over the South Korea Region. J Meteorol Soc Japan Ser 91(4): 545-554.
11. Uijlenhoet R (2001) Raindrop size distributions and radar reflectivity - rain rate relationships for radar hydrology. Hydrol Earth Syst Sci 5(4): 615-627.
12. Mapiam PP, Sriwongsitanon N, Chumchean S, Sharma A (2009) Effects of Rain Gauge Temporal Resolution on the Specification of a Z - R Relationship. J Atmos Ocean Technol 26(7): 1302-1314.
13. Yeo JX, Lee YH, Kumar LS, Ong JT (2012) Comparison of S-Band Radar Attenuation Prediction With Beacon Measurements, IEEE Trans. Antennas Propag 60(10): 4892-4900.
14. Terry AR, Scotte JS, Giangrande, Valery M, Melnikov (2005) Calibration Issues of Dual-Polarization Radar Measurements. J Atmos Ocean Technol 22: 1138-1155.
15. Van De Beek CZ, Leijnse H, Stricker JNM, Uijlenhoet R, Russchenberg HWJ (2010) Performance of high-resolution X-band radar for rainfall measurement in The Netherlands. Hydrol Earth Syst Sci 14(2): 205- 221.
16. Yu XT, Yu ZW, Rui XP, Li F, Xi YT, et al. (2012) Discussion about the Determination Methods of Weighted Centroid of dBZ on Vector Radar Echoes. Procedia Eng 29: 2240-2246.
17. Krajewski WF, Vignal B, Seo BC, Villarini G (2011) Statistical model of the range-dependent error in radar-rainfall estimates due to the vertical profile of reflectivity. J Hydrol 402(3-4): 306-316.
18. Mapiam P, Sriwongsitanon N (2008) Climatological ZR Relationship for radar rainfall estimation in the upper Ping river basin. ScienceAsia 34(1513): 215-222.
19. Chumchean S, Seed A, Sharma A (2008) An operational approach for classifying storms in real-time radar rainfall estimation. J Hydrol 363(1-4): 1-17.
20. Ozturk K, Yılmazer AU (2007) Improving the accuracy of the radar rainfall estimates using gage adjustment techniques: Case study for west Anatolia. Turkey Atmos Res 86(2): 139-148.
21. Bruen M, O’Loughlin F (2013) Towards a nonlinear radar-gauge adjustment of radar via a piece-wise method. Meteorol Appl 21(3): 675-683.
22. Villarini G, Krajewski WF (2009) Review of the Different Sources of Uncertainty in Single Polarization Radar-Based Estimates of Rainfall. Surv Geophys 31(1): 107-129.
23. Henschke Adjustment of the Z-R Relationship in Real-time for Use in South Florida,” in World environmental and water resources congress 2009, USA, pp. 6069-6080.
24. Gabella M, Bolliger M, Germann U, Perona G (2005) Large sample evaluation of cumulative rainfall amounts in the Alps using a network of three radars. Atmos Res 77(1-4): 256-268.
25. Nielsen JE, Jensen NE, Rasmussen MR (2012) Calibrating LAWR weather radar using laser disdrometers. Atmos Res Nov 122: 165-173.
26. Gabella M, Michaelides S (2007) Adjusting ground radar using space TRMM Precipitation Radar. In Advances in Measurement, Estimation and Prediction, (1st edn), springer, USA, pp. 493-514
27. Looper JP, Vieux BE (2012) An assessment of distributed flash flood forecasting accuracy using radar and rain gauge input for a physicsbased distributed hydrologic model. J Hydrol 412-413: 114-132.
28. Krajewski WF, Smith JA (2002) Radar hydrology: rainfall estimation. Adv. Water Resour 25(8-12): 1387-1394.
29. Matyas CJ (2010) Use of Ground-based Radar for Climate-Scale Studies of Weather and Rainfall. Geogr Compass 4(9): 1218-1237.