Engineering Technology Open Access Journal (ETOAJ)

**Implementation of A* Algorithm to Autonomous Robots-A Simulation Study**

Shrikant NA¹ and Selvakumar AA²*

Department of engineering, VIT University, India

Submission: February 13, 2018; Published: April 13, 2018

*Corresponding author: Selvakumar AA, Associate Professor, SMBS, VIT Chennai, India, Email: arockia.selvakumar@vit.ac.in

How to cite this article: Shrikant NA, Selvakumar AA. Implementation of A* Algorithm to Autonomous Robots-A Simulation Study. Eng Technol Open Acc. 2018; 1(3): 555564. 10.19080/ETOAJ.2018.01.555564

Abstract

This article presents some of the current contributions to the robotic path planning field. Reliable collision free path is the fundamental thing for proper working of autonomous vehicle/robots. In order to find an optimal path for robot, environment or workspace need to be understood correctly and suitable algorithm need to used. Many researchers developed different algorithm techniques as per the required operations. This paper presents an overview of strength and weakness of A* algorithm for static environment using distance formula. A* algorithm works on the lower details of the map hence, it is considered as a higher-level path planning technique. A* algorithm is based on the availability of adjacent nodes and distance of goal location from the current state of the robot.

Keywords: A* algorithm; Path planning; Hierarchical algorithms; Heuristics

Introduction

Autonomous robots attained genuine attention because of variety of applications in the household, industrial as well as military purpose. For the accurate performance of such mobile robots, navigation or motion planning is the key aspect. It includes perception of environment based on sensory data, configuring with the surrounding and decision making which is an important phase to find an optimal path from the start location to the goal location without any collision with the surrounding. Different algorithm techniques have been used the path planning of autonomous robots. For example, genetic algorithm, grid-based algorithms, geometry-based algorithms, sampling-based algorithms. Most commonly used technique for static environment is grid-based algorithm. It includes configuration space which is divided into no. of small grids and hence detecting the obstacles robot finds the path from start location to goal location in the configuration space. But, in order to find the optimum solution, i.e. collision free path with the shortest distance so as to minimize the travel time, distance formula is implemented with the A* algorithm [1].

A* algorithm is grid-based path planning technique. Basically, A* algorithm was initially designed for the graph transversal problems. Later, it was commonly used for path finding applications such as computer games. A* algorithm is practically easier and faster for implementation [2]. A* algorithm is suitable for the static environments only. Also, it is not good for obstacle shape changes. To reach the goal position, A* algorithm creates sub optimal paths with the help of neighboring grids. It is represented as f (n) = g (n) + h'(n) where, g (n) is the distance from the start position to the current position whereas h'(n) is the estimated distance from current state to the goal position. In order to find this estimation heuristic function is used. f(n) is nothing but the estimated shortest path from the start location to the goal destination. In this technique, distance formula is used as a heuristic function [3].

In practical situation, static environment may be large for this algorithm to solve. Such cases are solved by defining a hierarchical solution. A* algorithm works on probability-based maps, i.e., it always tries to find path with the smallest length having lowest probability of the collision with the surrounding. Here path length factor is dominant one. [3] Also, as the obstacle size increases probability of collision with the surrounding reduces drastically. [4] Stated in their article, A* algorithm is not suitable for the static environment with the smaller size obstacles as this algorithm tends to find shortest path only over the obstacle avoidance.

Problem Statement

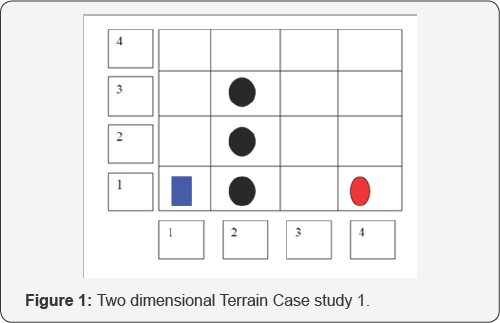
In the static environment, position or orientation of the obstacles are not changing. Hence configuration space is considered as a rectangular terrain, which can be divided into number of small grid. Initial and final location of robot or obstacles can be represented in these grids. Here, the problem is considered as a two-dimensional transverse terrain shown in the following Figure 1.

As shown in the Figure 1, configuration space is divided into number of grids. Autonomous robot is represented by blue dot. It has to transverse the terrain and reach the goal location which is represented by red oval. Black dots represent the obstacles.

Algorithm Guidance

Consider the case of a 4x4 configuration space. The starting node is (1,1). The successive node is only one in this case which is (1,2). There is no confusion, until the Robot reaches node (2,4). Now, there are two nodes (3,4) and (3,3). The successor node can be determined by evaluating the cost to the target from both the nodes (Figure 2).

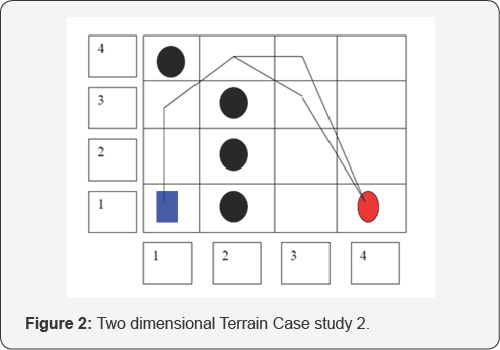
Now, f (n) for (3,3) is smallest of the two, hence the successor node is f (n) . The robot can now transverse to the node (3, 3) and continue expanding the successor nodes as above, until the goal location is reached.

Consider a configuration with dead end condition (Figure 3).

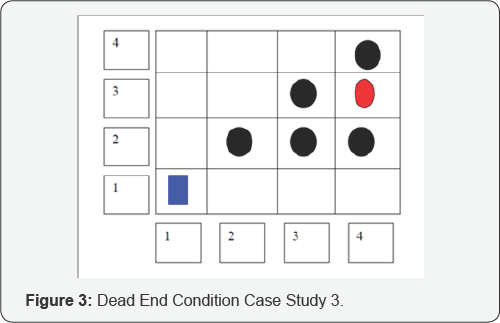
Here, from Node (2,1) will be chosen as the successor node instead of Node (1,2). The robot will continue to traverse the route until it ends up at the block at Node (4,1). Here, need to add an algorithm by which the robot find outs alternate paths once it ends up at a dead node (dead end). Avoids traversing paths that follows to a dead node.

This is achieved by keeping up two records OPEN and CLOSED. OPEN list contains successive paths that are yet to be computed and CLOSED list is having all paths that have been explored. The list OPEN also stores the parent node of current location. This is used at the end to trace the path from the Goal to the Start position, thus calculating the optimum path. The start node has 2 successors (2,1) and (1,2). From the initial calculation (2,1) is chosen and the robot travels along that node, however ones it reaches the dead end, it discards the node (2,1) and takes the second successor (1,2) and explores that route Figure 4.

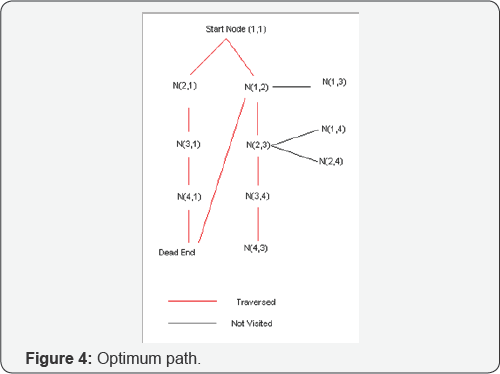
Once the goal location is reached the parent nodes are highlighted and tracked back to the start location to get the complete path. In the above example N(4,3),N(3,4), N(2,3), N(1,2), N(1,1) gives the optimum path. From the above conditions the following algorithm is obtained [3].

Algorithm Flow

Consider the first node and put it to the OPEN list. As it is the start point, is zero.

Now, next adjacent node's cost function is calculated. Smallest one is shifted to CLOSED list.

Suppose, robot reach to goal location, stop the algorithm. With the help of all cost functions, determine the path value. Otherwise, continue with the next nodes.

In the same manner, compute the cost function for all adjacent nodes with respect to robot's current position.

Now, with respect to parent node, sort the successor nodes to OPEN or CLOSED lists. Repeat the cycle till cost function of current location is zero (Distance between current location and goal becomes zero).

Simulation

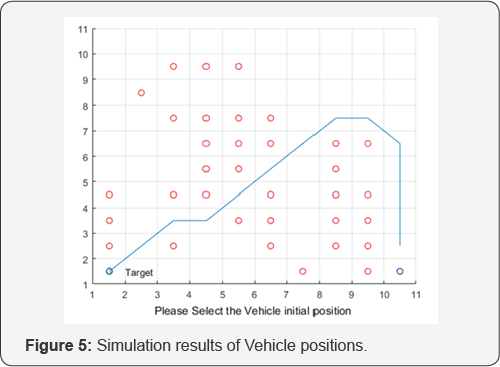
Simulation is carried out using MATLAB. Based on MATLAB coding, two-dimensional array of a configuration space is created. Autonomous robot's initial location and goal location we can assigned. Obstacles are assigned manually. From these above inputs we got the output as Figure 5.

Result

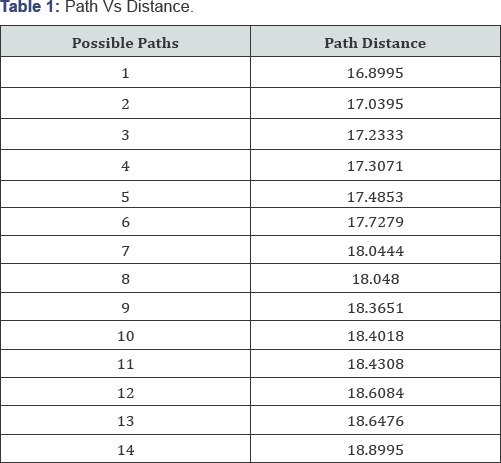
Hence, the optimum path is found out from start location to the goal location in a static environment using classification of open nodes and closed nodes based upon distance formula. This technique is successfully implemented to the different static environments as far as obstacles are in its definite shape and size. If we consider each grid of dimension 1x1 unit, following are the results from the simulation of the total distance of some possible paths [5-11]. From the results shows in Table 1, the available shortest path is highlighted in the Figure 5.

Summary

Hence, A* algorithm is successfully implemented to the static environment using MATLAB simulation. This technique of path planning finds the optimal path with respect to the distance, but practically there are chances of collision with the surroundings as distance is the dominating factor in this algorithm over obstacle avoidance. In order to serve this purpose, more accurate understanding of the environment is essential. Also, to get more optimum results with respect to distance, integration of this technique with neural network can be used. Future scope in this area refers to integration of this algorithm with genetic algorithm, i.e., simulation results of this algorithm can be treated as an initial population for genetic method for determining more optimized path.