Engineering Technology Open Access Journal (ETOAJ)

High Gain Observer for Sensorless Input-Output Linearizing Control for Induction Motor with Broken Rotor Bar Fault

A Menacer*, I Harzelli, Y Maanani and T Ameid

Laboratory of Electrical Engineering (LGEB), Biskra University, Algeria

Submission: January 07, 2018; Published: March 07, 2018

*Corresponding author: A Menacer, Laboratory of Electrical Engineering (LGEB), Biskra University, Algeria, Email: menacer_arezki@hotmail.com

How to cite this article: A Menacer, I Harzelli, Y Maanani, T Ameid. High Gain Observer for Sensorless Input-Output Linearizing Control for Induction Motor with Broken Rotor Bar Fault. Eng Technol Open Acc. 2018; 1(1): 555554. 10.19080/ETOAJ.2018.01.555554

Abstract

The aim of this paper is the broken rotor bar diagnosis for the sensorless nonlinear control (NLC) of the induction motor (IM). The strategy of control is based on the input output linearization control, using nonlinear high gain observer (HGO), in order to preserve the speed regulation and compensate the fault effect and to ensure the service continuity of the machine. The effect of the broken rotor bar is evaluated through the analysis of the direct current components Ids. This information can be used as an indication for the fault diagnosis.

Keywords: Induction motor; Diagnosis; Broken rotor bars fault; Nonlinear control; Input output linearization control; High gain observer

Abbreviations: IM: Induction Motor; FOC: Field Oriented Control; HGO: High Gain Observer

Introduction

The induction motor (IM) is known for its robustness, simplicity of operation and low costs and maintenance free. Like any motor exposed to mechanical or electrodynamics forces, it is lead to failures [1], it’s also may be caused by manufacturing fault, designing fault of the engineer, environment and poor technical knowledge of the job about in handling the motor [2].

On the other hand, vector control provides a good performance during transient and permanent phases. However, it requires knowledge of mechanical speed and rotor flux [3]. The difficulties of using field oriented control (FOC) arise from the modelling uncertainties due to parameter variation, magnetic saturation, load disturbances. To ensure a good dynamic performance, various robust control strategies for induction motor drives have been cited in the literature [4,5]. However, the input-output linearization control has focused attention owing to simple design, the perfect decoupling between the rotor speed and the flux, fast dynamic response, easy implementation and robustness to parameter variations, and also for load disturbances [6,7].

Fault detection in electrical machines has been the subject of researches for many years [8]. Vibration is used for the detection of mechanical problems, broken rotor bars and stator short circuits in induction motor. Vibration analysis techniques are usually installed on costly and sensitive machines, where the cost of such systems can be justified [9].

That is why some researchers are looking to analyze other quantities in order to solve this problem. In [10,11] d (direct) current axis components have been looked in closed-loop. The rotor speed and a rotor flux are estimated by high gain observer (HGO) [12,13]. The controller is based on the theory of feedback linearization. Where, the reduced model of IM in healthy and faulty states is used.

This paper is organized as follows. In section 2, the dynamic of the reduced model of IM is described. The input-output linearization control is designed for the speed and flux magnitude controls of an IM are showed in section 3. The HGO required for the rotor flux and rotor speed estimation are presented in section 4. Section 5, provides numerical simulation results of the proposed control technique in healthy and faulty states of the IM, followed by the conclusion.

Induction Motors Model with Broken Rotor Fault

The dynamic equations of IM can be expressed as follows [14]:

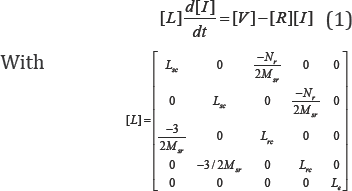
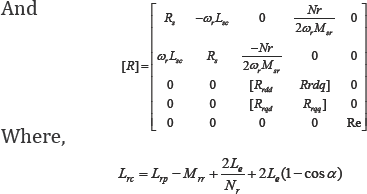
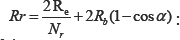Electrical angle of two rotor adjacent mesh�s.

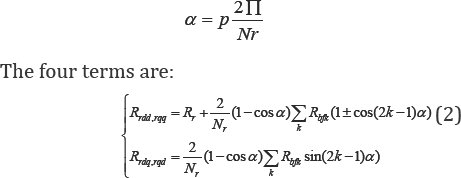
In Eq. 2, the summation is applied to all bars with fault. ^R_bfk is the increased resistance of the bar index k from its initial value before the fault.

The electromagnetic torque developed by the motor is expressed in terms of rotor currents and stator currents as:

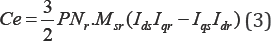
The model considered allows studying the behaviour at the healthy and faulty states of the IM in different operation cases.

Design of a Nonlinear Input-Output Feedback Linearizing Controller for Induction Motor

The input-output control problem is to find a state feedback such that the transformed system is input-output decoupled that is, one input influence one output only [15]. The technique requires measurements of the state vector x in order to transform a multi-input nonlinear control system:

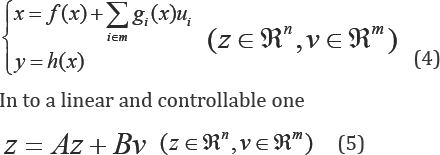
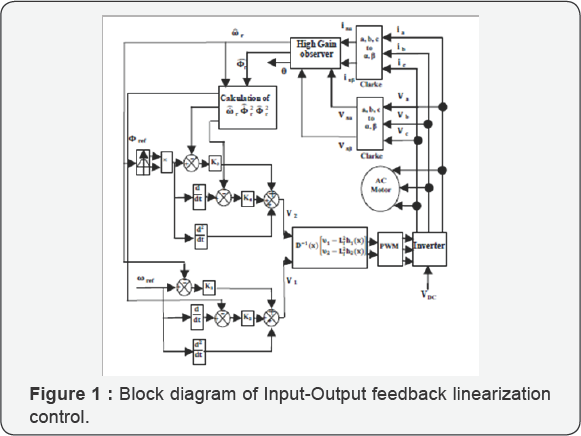
The control system is depicted in (Figure 1) [16]. The state space model of induction motor in the (a,P) frame coordinate is giVen by:

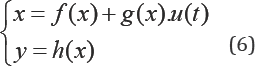
Where the state and commands vectors:

The decoupling matrix D(x) is singular if and only if Φ²_r zero which only occurs at the start up of the motor. That is, to fulfil this condition one can use in a practical setting, an open loop controller at the start up of the motor, and then switch to the nonlinear controller as soon as the flux goes up to zero. If the decoupling matrix is not singular, the nonlinear state feedback control is given by:

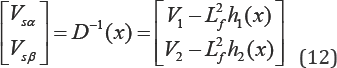
This controller linearizes and decouples the system, resulting in:

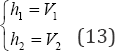
The closed loop system (13) is input-output decoupled and linear. To ensure perfect tracking of speed and flux references, V₁ and V₂ are chosen as follows:

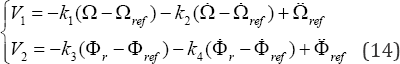
Nonlinear High Gain Observer Design for Induction Motor

The dynamic behaviour in general of the induction motor belongs to a class of relatively fast systems. For computational issue, the high gain observer which admits an explicit correction gain can be considered as one of the most viable candidate in the problem of state estimation [12,17]. To study the observation and control of the induction motor, we adopt this method in our model (6), given by:

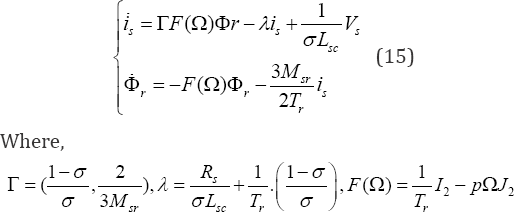
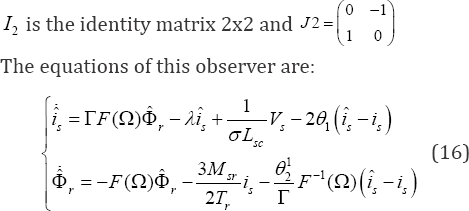
Where 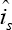and 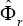are respectively the estimates of I_s and Φ_r , Which β₁, is a positive real. Therefore, the adaptive Scheme for speed estimation is given by:

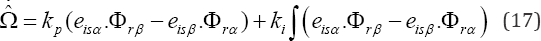
Where, 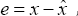, k and kt are respectively the proportional and integral constants.

Simulation Results

The sensorless input-output linearization control of induction motor used in healthy and faulty states: 1.1kW, 220V, 50Hz, 2-pole, a rotor with 16 bars were carried out using the Matlab/Simulink simulation package. The system parameters of the induction motor tested in this study are given in Appendix.

Healthy machine

To illustrate the performances of controller in healthy state of the machine, a simulation with reference speed equal to 1000rpm is realized in Figure 2, a nominal load torque equal to 3.5 Nm is applied at t=0.5s.

The electromagnetic torque follows the load torque and stator phase current have a very good dynamic. Quadratic rotor flux Φ_qr is maintained to almost zero, direct rotor flux Φ_dr tracks the reference values adequately well.

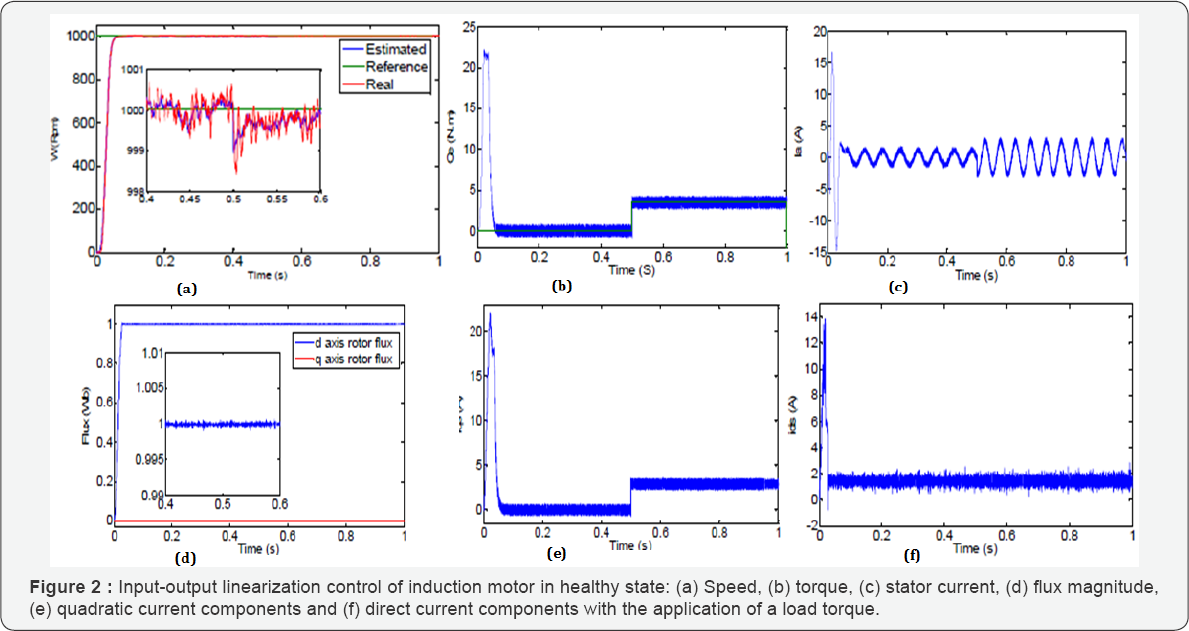
The speed reverse test is realized by changing the speed reference from 30 rpm to -30 rpm at t=1s with a nominal load torque 3.5 Nm is applied at t=0.5s in Figure 3.

The good performance such as robustness and convergence of the sensorless input-output linearization control when the induction motor operates in low reference speed. It shows that estimate rotor speed observer and the real rotor speed converge to the reference speed with very less errors.

Machine with adjacent two broken rotor bars fault

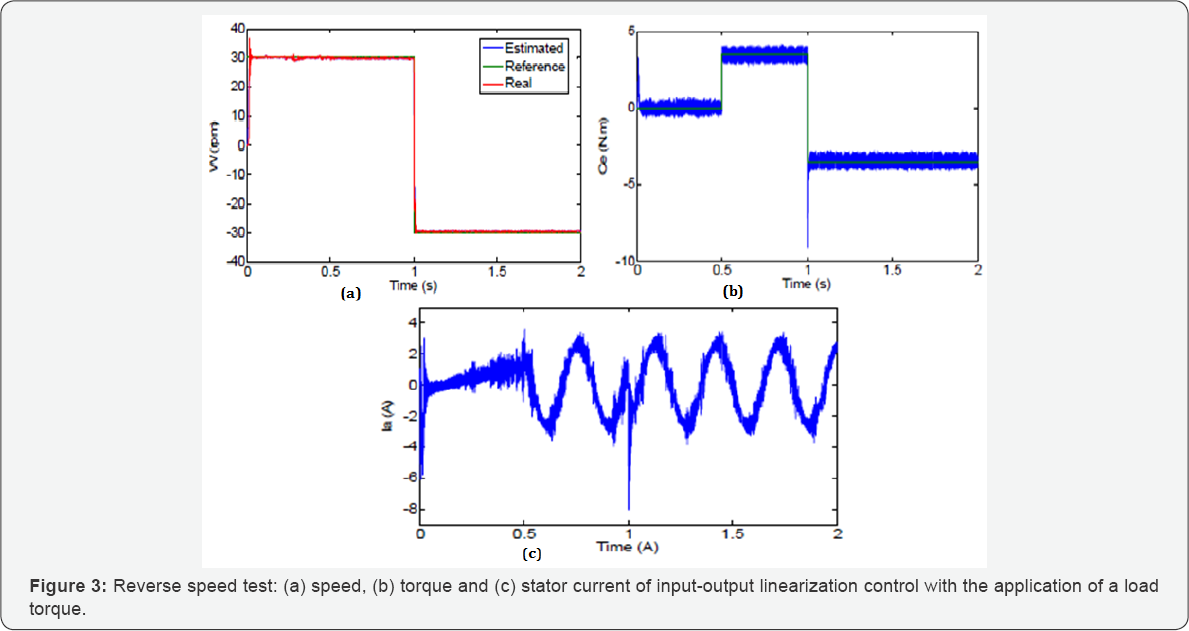
In this case the sensorless input-output linearization control of the induction motor with fault is considered. Two adjacent broken rotor bars fault are applied at t=1s and the machine operate at 1000 rpm with a nominal load torque 3.5Nm applied at t=0.5s.

The simulation results of sensorless input-output linearization control using high gain observer of the induction motor with adjacent two broken rotor bars fault are shown in Figure 4. The rotor speed and torque give no information about the fault effect, due to the closed loop of input-output linearization control which mask and compensate the effect of the fault. However, the direct current Ids is affected by the fault through the fluctuations. This information can be exploited for the online diagnosis of the machine in closed loop.

Conclusion

In this paper, a sensorless input-output Linearizing control for the induction motor is considered with broken rotor bars fault. The controller shows a good performance of the induction machine control in healthy and faulty states.

Therefore reveals a powerful sensorless input-output Linearizing control using high gain observer for estimate the rotor speed and Flux, Where The effect of loop control by using the speed regulator ensures the rejection of ripples, therefore the correlation with the fault severity is lost. The fault effect didn't affect the rotor speed; unlike the direct current components I_ds which offer a good indication for the fault effect in closed loop.