Textile Science Engineering Journal

Analysis of Printed Fabric Pattern Segmentation Based on Unsupervised Clustering of K-Means Algorithm

**Ruru Pan*, Charles Kumah & Ning Zhang**

School of Textiles and Clothing, Jiangnan University, Wuxi, Jiangsu, China

Submission: October 05, 2017; Published: November 27, 2017

*Corresponding author: Ruru Pan, School of Textiles and Clothing, Jiangnan University, Wuxi, Jiangsu, China, Email: prrsw@163.com

How to cite this article: Ruru P, Charles K, Ning Z. Analysis of Printed Fabric Pattern Segmentation Based on Unsupervised Clustering of K-Means Algorithm. Curr Trends Fashion Technol Textile Eng. 2017; 1(4): 555568. DOI: 10.19080/CTFTTE.2017.01.555568

Abstract

Fabric segmentation has recently increased widely in diverse fields of computer technology of which printed fabric pattern is of no exception. This is due to the fact original printed fabric is just inadequate to extract suitable information for further applications. In textile industry, automation inspection for pattern recognition helps not only to improve fabric quality but also to reduce cost and wastage of time since human inspection is not 100% guaranteed. Printed fabric samples are washed, ironed, scanned and then preprocessed with median filter and segmented by k-means clustering algorithm. In this paper, we present a thorough analysis of k-means algorithm on printed fabric pattern as input data considering time taken on the unsupervised clustering. Thorough analysis of experimental results demonstrated that the complexity in clustering has reduced to its minimal with good application specific and good time yield.

Keywords: Printed fabric pattern; Image segmentation; K-means clustering

Introduction

The term image segmentation refers to subdivisions of an image or pattern into its constituent regions or object. This is one of the most important aspects in textiles industries to identify regions that differ from a uniform background and help to improve fabric quality and consequently reduce labor cost. Printed fabric pattern segmentation however, is the partitioning of fabric pattern into a set of disjoint regions with uniform and similar characteristics such as color, texture, intensity, etc. Different methodologies have been projected [1-3] regarding the subject. Segmentation algorithms have been categorized as threshold, clustering, contour detection and region extraction.

Fang et al. [4] anticipated an orderly technique for finding the initial centroids. The centroids obtained by this method are reliable with the distribution of information on the fabric pattern. In a related development, Fahim et al. [5] proposed a resourceful method for passing on original information to clusters. These works produced clusters with better precision, compared to the initial k-means algorithm. On the contrary, these techniques do not advocate any improvement to the time complexity of the k-means algorithm. Sheetal et al. [6] recognized fabric defect detection using the K-Means clustering algorithm. Cluster analysis [7] is one of the major data analysis methods which are extensively used in the above practical applications. Even though k-means algorithm [7-9] proved to be effective in many applications, its complexity seems to be a major drawback thereby causing slightly poor-quality clustering exclusively for a bulky data input.

In this paper, we analyze time specific by comparing k-means clustering and fuzzy c-means algorithms since the two perform the same function expect that fuzzy c-means has membership function. Printed fabric patterns were scanned and preprocessed by median filtering technique to remove extraneous influencing factors and further segmented with k-means algorithm. K-means algorithm is widely used in this field. K-means initially pick centroid at random resulting in several types of clusters. The objective here is to classify a given input data (printed fabric) into k number of disjoint clusters, where the value of k is fixed in advance. This algorithm was conducted on a number of printed fabrics and noted that k-means is very application specific, time sensitive and has fast operation.

Experimental Methodology

Image capture

Two experimental digital printed fabrics were captured by CANONSCAN 900F MARKII PHOTO scanner with the resolution of 100 dpi. The size of each is 6 inches x 6inches. The captured pattern consisted of 600 pixels x 600 pixels. Median filter was used to preprocess the fabric appearance to reduce color differentiation that resulted due to influencing factors added during scanning [10].

K-means clustering algorithm

The algorithm involves two steps: the first step is to define k centroids, one for each cluster. The next step is to take each point belonging to the given pattern and associate it to the nearest centroid. Euclidean distance is generally considered to determine the distance between data points and the centroids. When all the points are included in some clusters, the first step is completed and an early grouping is done. At this point we need to recalculate the new centroids, as the inclusion of new points may lead to a change in the cluster centroids. Once we find k new centroids, a new binding is to be created between the same data points and the nearest new centroid, generating a loop. As a result of this loop, the k centroids may change their position in a step by step manner. Eventually, a situation will be reached where the centroids do not move anymore. This signifies the convergence criterion for clustering [11,12].

K-means presents the following advantages among others: it is fast and efficient in terms of computational cost, simple and easy to implement, easy to interpret clustering results, clusters have similar density.

K-means clustering algorithm:

Input:

P = {p1,p2,...pn} //set of n datasets

k //Number of input cluster

Output:

A set of k clusters

Steps:

1. Randomly pick centroids all over the dataset and find Euclidian distance from each of the data point from the centroids.

2. Find/calculate Euclidean distance with respect to the centroid

3. Assign data points to the clusters and re-compute the centroids - the data points should be assigned to some temporal clusters and average out all data points in the given temporal clusters and find the value of a new centroid

4. Repeat until the centroid does not vary much-at its optimum point, the algorithm is reached.

Experimental Results and Discussions

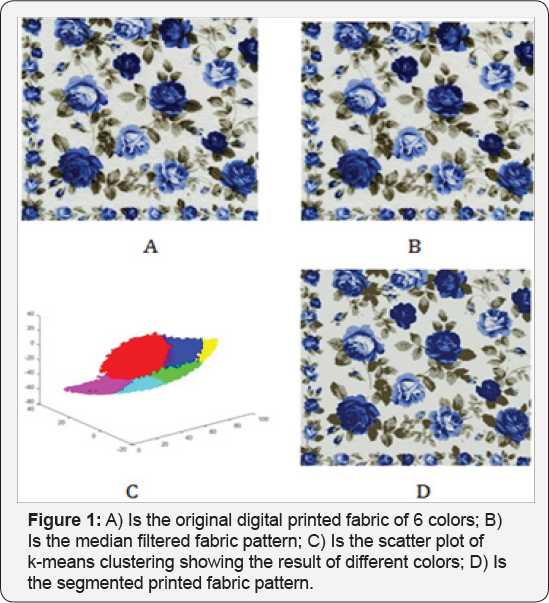
The (Figures 1A-1D) below show original digital pattern, median filtered pattern, scatter plot and segmented pattern of a 6-color fabric with 600pixels x 600pixels. The original printed fabric was captured preprocessed with median filtering technique and segmented with k-means clustering algorithm.

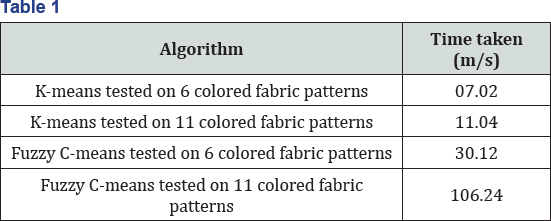
For fabric segmentation analysis, the unsupervised clustering algorithm requires initial value as input. In the case above, the value of k is 6. Even though there were slightly poor quality of clustering, k-means application has proved to be specific, time sensitive and hence very fast operation. Due to the fact that the input data (printed fabric) is not too bulky, the segmentation process lasted for 07.02(m/s) as the total time yield whereas, fuzzy c-means recorded 30.12 (m/s). k-means is however fast and efficient in terms of computational cost (Figures 2A-2D).

In a related development, k-means was conducted on quite a bulky data which has k value to be 11. It was noted that time yield for this experiment has increased to 11.04(m/s) whereas for fuzzy c-means, it recorded 106.24(m/s). The figures below, show the 11-colored printed fabric pattern [13,14].

Comparison of Results of K-means and Fuzzy C-means Algorithms

The slightly poor-quality clustering observed for k-means, was exclusively due to huge data input. Nevertheless, k-means algorithm performs efficiently than fuzzy C-means algorithm Table 1.

Conclusion

K-means is the most widely algorithm used for clustering dataset. It has proved to be the most important algorithm for image/pattern segmentation despite a slight drawback.

After experimenting with digital printed patterns with diverse textures and illuminations, it shows that k-means algorithm performs much faster. It was also noted that k-means and fuzzy c-means algorithms perform the same function except that fuzzy c-means has addition of membership function and takes into consideration soft clustering.

Owing to the experimental results conducted on printed fabric patterns, k-means clustering algorithm is very application specific, time sensitive and very fast operation hence more desirable to fuzzy c-means algorithm.

Based on the above findings, I will like to explore more into other unsupervised clustering algorithms like Self-Organizing Map (SOM) and Density Based Spatial Clustering Application with Noise (DBSCAN) for the segmentation process in printed fabric patterns.