Mini Review

Optimal Operating Policy of a Fluidized Bed Bioreactor used for Mercury Uptake from Wastewaters by Using Immobilized P. Putida Cells

Gheorghe Maria* and Andreea Georgiana Şcoban

Department of Chemical & Biochemical Engineering, University Politehnica of Bucharest, Romania

Submission: March 16, 2017; Published: March 27, 2017

*Corresponding author: Gheorghe Maria, Department of Chemical & Biochemical Engineering, Politehnica University of Bucharest, Splaiul Independentei 313, Bucuresti 060042, Romania, Email: gmaria99m@hotmail.com

How to cite this article: Gheorghe M, Andreea G. Optimal Operating Policy of a Fluidized Bed Bioreactor Used For Mercury Uptake from Wastewaters by Using Immobilized P. Putida Cells. Curr Trends 005 rends Biomedical Eng & Biosci. 2017; 2(4): 555594. DOI: 10.19080/CTBEB.2017.02.555594

Abstract

A model-based analysis of a three-phase continuously operated fluidized-bed bioreactor (TPFB) is developed in order to determine the multi-objective optimal and sustainable operating policy of a TPFB used for removing mercury ions from wastewater. More specifically, the analysis is focus on finding the optimal feeding policy of alginate porous beads of known particle size containing immobilized biomass (P putida bacteria) that minimize the biomass consumption, while keeping a quasi-constant high mercury removal conversion, under quasi-stable reactor performances. The extended bioreactor model is accounting for the biomass growth, biodegradation, and its partial leakage and washout. Bioreactor dynamics prediction has been generated by using a simple Michaelis-Menten kinetic model adopted from literature. The resulted optimal feeding policy of the bioreactor points out the importance of the adoption of an extended and adequate process/reactor model able to solve difficult engineering operation problems by quickly adjusting the feeding conditions according to the time-varying characteristics of the biomass culture, and to the limited possibilities to control the process during the wastewater residence time in the bioreactor.

Introduction

Over the last decades, there is a continuous trend to develop more and more effective bioreactors for development of various biosyntheses by producing fine-chemicals or organic compounds in the food, pharmaceutical, or detergent industry, using cell culture batch (BR), semi-batch (fed-batch, SBR), continuously operated fixed-bed or three-phase fluidized-bed (TPFB) reactors, or mechanically agitated continuous reactors (MACR) [13], aiming to replace complex chemical processes, energetically intensive and generating toxic wastes. It is to be mentioned, among these, the fermentative processes for production of organic acids, alcohols, vinegar, amino-acids/proteins, yeast, hydrogen, food products and additives, recombinant proteins, etc., by using bioreactors with microbial/cell cultures [1,2] or bioreactors for waste removal in water treatment plants [3], with various cooling and aeration systems in simple or sophisticate constructive alternatives [2].

However, the bioreactor optimal operation is one of the most difficult and challenging engineering problem, due to well- known bioprocess complexity and variability, besides the large number of variables influencing the bioprocess difficult to be accounted in a quite reduced kinetic model. This paper is aiming at using a multi-objective criterion and an elaborated bioreactor model to derive sustainable optimal operating policies of a TPFB used for mercury uptake from wastewaters by immobilized cultures of P putida.

The target optimization criteria concern the sustainability of the TPFB operation, leading to the concomitant optimality of:

I) An economic criterion (maximum of mercury removal conversion);

II) A safety-stability criterion (quasi-stationary removal conversion over a defined time-horizon);

III) An environmental criterion (minimum wasted biomass with mercury traces leaving the TPFB).

To solve this complex multi-objective optimization problem, the “weighting function method” has been used, by associating to each criterion and formulated objective function weighting factors chosen depending on the relative importance given to each objective. In the present case, the weights w_xHg , w_σ, and w_x correspond to the conversion maximization criterion, to the conversion stability criterion, and to the biomass consumption minimization criterion respectively.

To simulate the TPFB reactor performances for deriving the optimization problem solution, an extended dynamic ideal model of the bioreactor was adopted [4], including a simple Michaelis-Menten kinetics of the bioprocess, thus allowing its use for optimization purposes. The model includes the main characteristics of the bioprocess on the solid support, and the solid-liquid-gas interfacial transport of the mercury, even if additional calculations are necessary to derive the particle effectiveness and to solve the mass flux equality at solid-liquid- gas interface at quasi-steady-state on every small considered time interval during the transient regime simulation. The extended bioreactor model is accounting for the biomass growth, biodegradation, and its partial leakage and washout.

For the formulated multi-objective optimization problem using normalized objective functions associated to the three mentioned criteria, the best TPFB reactor operating policy was obtained for the relative weights: w _xHg = w_σ = 1; W_x = 0.1, by giving less weight to the biomass consumption, thus ensuring a maximum conversion, but also quite-uniform over the running time, with the expense of a higher consumption of biomass. This operating policy is preferred because the biomass is cheap and renewable, while the removal of mercury from wastewater is a very important ecological issue deserving lots of investments, and operational costs.

Process description and mercury reduction kinetic model

The approached bioprocess in this paper, called “microbial detoxification“ of wastewaters involves metabolic processes of certain cell cultures, that results in reducing the mercuric ions from wastewaters to elementary volatile mercury, which is removed by the micro-organisms and then easily removed from the TPFB liquid being recovered by the sparged air and, eventually recovered in a subsequent condenser/adsorption device. Among the resistant strains used for this purpose in the TPFB are to be mentioned [4,5]: Pseudomonas sp; Aeromonas hydrophila; Escherichia coli, usually immobilized on a porous support to prevent biomass quick inactivation, leakage and washout. The mercury ions diffuse into the cells. The mercury ion reduction to metallic mercury takes place inside the living cells with a high efficiency, the mer-reductase/NADPH used being continuously synthetized and regenerated during the cell growth (Figure 1).

This new technology of heavy metal removal from polluted surfaced waters is based on the natural defence system of some bacteria. Instead of “neutralizing” the toxic mercuric ions by consuming a lot of cell energy and metabolites, the bacteria developed an efficient defence system by simply reducing the ions to volatile, less toxic and easily eliminable metal from the cell, by membrane diffusion and then evacuation by the bubbled air. The whole uptake process is metabolically adjusted by a genetic regulatory circuit controlling the mer operon expression. At least seven mer-genes are involved in this process [6,7], the ratio of their expression being controlled according to the cytosolic content of mercury. The resulted cross- and self-control of the mer operon expression is aiming at eventually “shrinking” the import of large amounts of mercury, which might lead to the blockage of RSH cell species, exhausting the cell resources, and eventually compromising the whole cell metabolism”[5].

overall Michaelis-Menten type kinetic model proposed by Deckwer et al. [8] for P.putida sp. cells has been adopted (Table 1). Based on experiments using modified E. coli cell cultures, Philippidis et al. [9] and Deckwer et al. [8] completed the bioprocess kinetic model, by including a second-order inhibition by the substrate [4], and proved that mercury membranar permeation is the slowest process step, by using separate experiments conducted with cultures of intact cells or "permeabilized" cells to ionic species. Eventually, a reduced Michaelis-Menten model for mercury uptake by E. coli cells has been proposed, with the adjustable rate constants being function of the copynumbers of mer-plasmids existing in the cloned cells [9] . It has been eventually concluded that modified E. coli cells reported an increased efficiency to remove mercury ions up to a certain limit (controlled by the permease proteins), which did not exhaust the internal cell resources.

A more sophisticated/structured cell model existing in the literature [5-7,11] is not a feasible alternative for the present optimization study, because its coupling with the bioreactor model leads to a very extended bioreactor model that requires a too high computational effort to be solved.

Plant operation, reactor model, and nominal operating conditions

The analyzed TPFB bioreactor is the scale-up of the bench- scale TPFB used by Deckwer et al. [8] to investigate the removal of mercury ions from wastewater using P putida sp. separately immobilized on porous alginate granules of 0.9-1 mm average diameter (Figure 2).

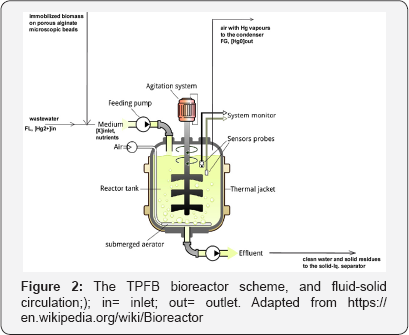
The approached TPFB bioreactor is continuously operated: the wastewater with suspended alginate beads of microscopic size are continuously fed in and evacuated from the bioreactor. The optimal growing conditions of the immobilized biomass is ensured by an excess of sparged air, and nutrients added initially and during TPFB operation, in a recommended mass ratio of C/N/P= 100/5/1, that is a mixture of sucrose 167 g/L, urea, and sodium phosphate buffer 0.25 M[4]. The reactor and carrier characteristics, and the nominal (reference) operating conditions are those presented by Scoban & Maria [4].

A good diffusion of the substrate (mercuric ions) to bacteria is assumed taking place in the large support pores, while an equilibrated biomass metabolism is ensured by the added nutrients in the fed wastewater. The liquid flow rate (or equivalently the liquid residence time), the aeration rate (in a high excess vs. metabolic requirements), pH, and temperature are tightly monitored to ensure a sustainable bioprocess. The biomass content in the bioreactor varies due to several reasons, all being accounted for in the bioreactor model: biomass growth, biomass degradation, and its leakage due to the hydrodynamic stress. The biomass level in the reactor is continuously adjusted by means of an optimal biomass feeding policy to be determined by using suitable optimization objectives (below discussed), by accounting for the biomass consumption due to the continuous purged biomass/support together with the evacuated treated water, biomass growth, and its biodegradation.

The resulted metallic mercury at the micro-organism cytosolic level, quickly diffuses through the cell membrane and then through support pores toward the pseudo-homogeneous bulk liquid phase. Because the mercury solubility in the water is very low, it quickly diffuses through the gas-liquid interface, being transported by the sparged air outside the bioreactor. The outlet gas containing the volatile metallic mercury is passed then through an condenser/adsorption device for recovering the metal.

The mathematical model of the TPFB is those of Scoban & Maria [4]. In short, the TPFB model main hypotheses are the followings: perfectly mixed liquid and gas phases, of quasiconstant volumes; dynamic, isothermal, iso-pH operation; the solid carrier and biomass are continuously fed-in and evacuated- from the bioreactor, together with the wastewater; quasiconstant activity of the living biomass; the solid particles (of uniform characteristics) are considered uniformly distributed in the homogeneous liquid phase, due to the well-mixing conditions; the low amounts of mercury bio-accumulated into bacteria, are neglected in the model.

The mercury ions diffuse from bulk phase through the external diffusional film surrounding the particles and then through the internal pores until reaching the immobilized biomass where the mercury is crossing the cell membrane, and then it is reduced to metallic mercury (Figure 1). The resulted metallic mercury from the cell cytosol diffuses through the cell membrane and then it is transported as micro-drops (of ca. 5 μm diameter), or dissolved (solubility of 26 μg L^-1 at 26^oC) to the gas-liquid interface from where it passes as vapours into the homogeneous gas phase (air). Low amounts of mercury bioaccumulated into bacteria, are neglected in the model. Mercury mass balance in the liquid and gas phases includes the inlet- outlet and transport terms [4].

Formulate the multi-objective optimization problem

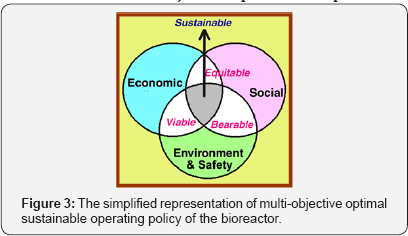
To get an optimal and sustainable operating policy of the TPFB, a multi-objective performance criteria should be formulated, concomitantly considering optimization of the following objectives (Figure 3):

I) An economic objective ensuring economic benefits, such as high reactor productivity, conversion, yield;

II) A safety-stability objective, ensuring that the chemical reactor setpoint present a low probability of reactor runaway; for a bioprocess this criterion is related to ensuring a quasiconstancy of the output quality/reactor performance and control aspects;

III) The environmental criterion is related to the minimum production of wastes, and by-products, thus the reactor outputs presenting a minimum environmental impact.

In the present case study, one consider optimization of the TPFB bioreactor over a time-horizon of running-time of 0 ≤ t ≤ 300 min .

The three mentioned objective functions are formulated as followings:

a) Economic objective: Maximum of the average mercury ion reduction conversion 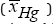, over the considered runningtime interval tε[0, 300] min. which, in mathematical terms is equivalent to:

Minimum of 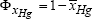, where the integral average of the conversion is evaluated with the relationship: =

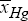b) Stability objective: This criterion is formulated as minimum standard deviation (denoted by a) of the output conversion x_Hg from its average value over the considered running-time interval of tε[0, 300] min, that is:

Minimum of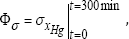

where: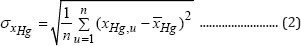

(n denotes the number of running times when conversion was predicted by the TPFB model). This objective ensures minimum deviations of the output conversion from its average value, thus ensuring a quasi-constant bioreactor performance over the considered running-time interval.

c) Environmental objective: This criterion is formulated as minimum biomass consumption in the continuous TPFB bioreactor because the solid carrier (alginate beads) with the immobilized biomass are continuously fed-in and evacuated- from the bioreactor, together with the wastewater. The minimum biomass consumption over the considered running-time interval tε[0, 300] min, is equivalent to:

Minimum of

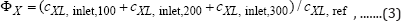
with the reference value of C_XL,ref = 1000 mg/L taken to normalize the Φ_X value to make it comparable to Φ_xHg and Φ_σ objectives.

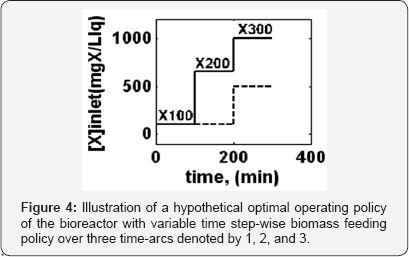
Notations ^CXL,inlet,100,^CXL, inlet,200 ,^CXL, inlet,300 define the inlet biomass concentrations over chosen three time- arcs of the running time of interest, that is:

^CXL,inlet,100 is [X]inlet for 0 ≤ t ≤ 100 min

^CXL,inlet,200 is [X]inlet for 100 ≤ t ≤ 200 min

^CXL,inlet,230 is [X]inlet for 200 ≤ t ≤ 300 min

Optimization of the TPFB operation is looking for the vector of unknown biomass inlet concentrations kept constants over each considered time-arc, that is:

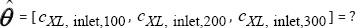
such that to be concomitantly realized the minimum of ^ΦxHg, Φ_σ , and Φ_X . The problem is difficult to be solved because some criteria are synergistic 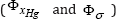, but others are antagonistic 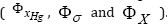. In the literature, there are several numerical methods to solve this problem [12]. For instance, when two contrary objectives are present, one method is to generate the Pareto-front, that is the all optimal solutions that realize the best trade off between adverse objectives. A Pareto solution is one where any improvement in one objective can only take place at the cost of another objective.

In the present paper, we have used a simpler procedure based on constructing a hybrid (composite) objective function by summing the individual objectives multiplied by subjectively adjustable weights denoted by w_J ∈[0,1]. This multi-objective optimization method is known as the “weighting function method” [2]. Even if less rigorous, this optimization method is very simple and computationally tractable.

In the present case, the optimization problem is reduced to:

[ ^CXL, inlet,100 ; ^CXL,inlet,200 ; ^CXL, inlet,300 ] = argMin

The weighting factors W_J ∈[0,1] associated to the objective functions are chosen depending on the relative importance given to each objective. Searching variables vector 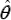previously defined will be estimated while the other process variables are kept at the nominal conditions.

Illustration of such a hypothetical optimal operating policy of the bioreactor with variable time step-wise biomass feeding policy over three time-arcs denoted by (X100) ^CxL, inlet,100 , (X200) ^CXL, inlet,200, and (X300) ^CXL, inlet,300 is given in Figure 4.

Results and Discussion

Solution of the optimization problem (4) has been made in two alternatives:

Operating policy (A) by giving equal weights to the three objective functions (i.e. economic, stability, and environmental criteria) in the composite multi-criteria objective ϕ_A, that is w_xHg = W_σ = W_X = 1 in equation(4).

Operating policy (B) by giving less importance to the biomass consumption in the composite multi-criteria objective ϕ_B, that is w_xHg = W_σ = 1, and W_X = 0.1 in equation (4).

The obtained optimal operating policies are presented in Figure 5a in terms of (X100) c_XL,intel,100, (X200) ^CXL, inlet,200 , and (X300) ^CXL, inlet,300, and in Figure 5b in terms of realized mercury removal conversion and its concentration in the reactor. The optimal values of each objective function is given in the Table 2.

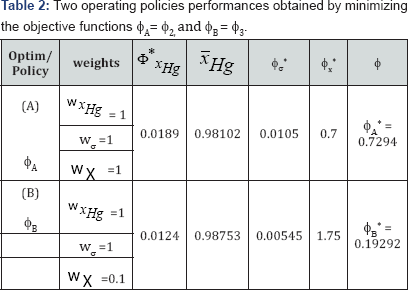
It is to remark that, The operating policy (A) is not very convenient, because, as revealed by the plots of Fig. 5b, the conversion even if high (average 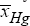=0.98102), is not uniform, presenting a quite large standard deviation from the average, that is 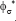=0.0105. On the contrary, the operating policy (B) realizes a higher average conversion ( 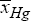= 0.98753) but also quite-uniform over the running time, with minimum deviations from its average value of 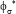=0.005455, thus ensuring a quasiconstant bioreactor performance over the considered running time, The cost of the higher performances of the optimal policy (B) vs. (A) is a higher consumption of biomass ( 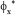= 1.75 vs. 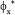= 0.7). In spite of such a drawback, the operating policy (B) is still preferred because the biomass is cheap and renewable, while the removal of mercury from wastewater is a very important ecological issue deserving lots of investments, and operational costs.

Conclusion

Derivation of alternative optimal operation policies of a TPFB bioreactor used for testing mercury removal efficiency by using immobilized bacteria on a suitable porous support (alginate beads) is an essential engineering analysis to be used in further process scale-up and control.

In the simulated case study, the very effective bacteria metabolism allows an efficient reduction of the cytosolic mercury (92-99% conversion), excretion and transport of the volatile metal to the gas phase for a high pollutant load in the wastewater. By keeping a reasonable small size of alginate particles (1-2 mm), the most important control parameters appear to be the biomass load in the bioreactor and the wastewater/biomass feed flow rate.

References

1. Liese A, Seelbach K, Wandrey (2006) Industrial biotransformations. Wiley-VCH, Weinheim.
2. Ghose TK, Fiechter A, Blakebrough N (1978) Advances in Biochemical Engineering. Springer-Verlag, Berlin 7(10): 1977-1978.
3. Negulescu M (1987) Epurarea apelor uzate industrial. Tehnica publ, Bucuresti, Romanian.
4. Scoban AG, Maria G (2016) Model-based optimization of the feeding policy of a fluidized bed bioreactor for mercury uptake by immobilized P. putida cells. Asia-Pacific Journal of Chemical Engineering 11(5): 721734. DOI: 10.1002/apj.2003.
5. Maria G, Luta I (2013) Structured cell simulator coupled with a fluidized bed bioreactor model to predict the adaptive mercury uptake by E. coli cells. Computers & Chemical Engineering 58: 98-115. DOI: 10.1016/j.compchemeng.2013.06.004.
6. Maria GA (2009) whole-cell model to simulate the mercuric ion reduction by E. coli under stationary and perturbed conditions. Chemical and Biochemical Engineering Quarterly 23(3): 323-341.
7. Maria G (2010) A dynamic model to simulate the genetic regulatory circuit controlling the mercury ion uptake by E. coli cells. Revista de Chimie 61(2): 172-186.
8. Deckwer WD, Becker FU, Ledakowicz S, Wagner-Döbler I (2004) Microbial removal of ionic mercury in a three-phase fluidised bed reactor. Environmental Science and Technology 38(6): 1858-1865.
9. Philippidis GP, Malmberg LH, Hu WS, Schottel J (1991) Effect of gene amplification on mercuric ion reduction activity of Escherichia coli. Appl Environ Microbiol 57(12): 3558-3564.
10. Doran PM (1995) Bioprocess engineering principles, Elsevier, Amsterdam.
11. Maria G, Luta I, Maria C (2013) Model-based sensitivity analysis of a fluidised-bed bioreactor for mercury uptake by immobilised Pseudomonas putida cells. Chemical Papers 67(11): 1364-1375. DOI: 10.2478/s11696-013-0403-z.
12. Rao SS (2009) Engineering optimization- Theory and practice. Wiley, New York, USA.
13. Maria G (2012) Enzymatic reactor selection and derivation of the optimal operation policy by using a model-based modular simulation platform. Computers & Chemical Engineering 36(1): 325-341. DOI: 10.1016/j.compchemeng.2011.06.006.

Dr. Gheorghe Maria is currently professor in Chemical & Biochemical Reaction Engineering with the UPB - University Politehnica of Bucharest (Romania). He received the PhD in 1987 in chemical engineering at UPB (supervisor Prof. Dr. ing. Raul Mihail). On 1982 he joined ICECHIM (catalysis, and chemical & biochemical energetics divisions, as a senior researcher), and on 1990 he joined UPB as a lecturer. On 1992 he come in Switzerland for working as Assistant Professor with ETH Zürich (with the late Prof. David W.T. Rippin group of Process System Engineering). On 1997 he return to Romania becoming Associate Professor and then full Professor (1999) with UPB. His research interests concern the fields of (bio)chemical reactor and kinetic modelling, biochemical engineering and bioinformatics, risk analysis of chemical plants, modelling of cell metabolic processes, gene expression and regulatory circuits, and drug release kinetics. Over the past 25 years he participated to various intl. projects, making short research stages/visitingship at ETH Zürich (3-months on 1997, SNSF fellow on environmental risk analysis), Univ. des Saarlandes (3-months on 1999, DAAD fellow on modelling complex enzymatic kinetics), TU Erlangen (3-months on 2000, catalytic membrane reactors), Texas A&M University (2002-2003, NIH fellow on modelling gene expression and gene regulatory networks, synthetic biology), TU Braunschweig (2006) and TU Hamburg (3-months on 2009, DFG and DAAD fellows on simulating bacteria resistance to environmental pollutants), Tianjin Inst. Ind. Biotechnology (2-months on 2010, in-silico searching for gene knockout strategies for E. coli cell, synthetic biology). He presented more than 25 invited Lectures at various Universities in EU, CAN, USA (among them: Princeton Univ., Texas A&M University, EPFL Lausanne, Queen's Univ. Kingston- Canada, BASF Ludwigshafen), authored 12 books and teaching books, 5 book chapters, 130 papers in peer reviewed ISI international journals and univ. journals, and 77 in intl. conference proceedings, with more than 1000 citations (h-index 17 and i10 index 36; ResearchGate score = 34.76). According to the Romanian ranking system, he reported high scores signing NP=86 ISI papers as principal author, with a cummultative impact factor of FIC= 124.48, with a total of more than 1000 citations (Googleschoolar). He is a reviewer for many (bio)chemical engineering journals (19), and co-chaired 13 international conferences. On 1985 he award the Prize of the Romanian Academy (for kinetic studies and scalep of the methanol-to-gasoline process at Brazi petrochemical works). He is member in the scientific/editorial board of Chem. & Biochemical Eng. Q. (Zagreb), Revista de Chimie (Bucharest),

The Scientific Bulletin of University POLITEHNICA of Bucharest, Bulletin of Romanian Chemical Engineering Society, ECOTERRA Journal of Environmental Research and Protection (edited by Romanian Society of Environmental Sciences and Engineering, Cluj-Napoca Romania). He was also an expert for various EU / national research programs, being also a PhD supervisor at UPB (from 2008, in Chem. & Biochem. Eng. topics), with 5 PhD-s finalized, and 4 PhD-s in progress.

Chem. Eng. Andreea Georgiana Şcoban received her BSc (2015), and MSc (2017) in Chemical & Biochemical Engineering from University Politehnica of Bucharest (Romania) UPB, being currently a PhD student candidate with the Dept. of Chemical & Biochemical Engineering. In the high-school she participated to a large number of competitions (so-called national and international olympics) in Chemistry, winning several awards, such as bronze medal at the Chemistry Olympics in Tuymaada in Yaccutia (2010), and silver medal at the “D.I. Mendeleev” Chemistry Olympics in Moscow (2011). Even though she is still a young but very ambitious researcher, she coauthored 5 papers in international ISI journals. On 2015 she won the 1st prize at the scientific communication conference of chemical engineering BSc students at UPB, by presenting an original and valuable communication in the subject of this paper.