Short Communication

Some Mechanical Equilibrium Problems. A Geometrical Point of View

Ion Mierluș-Mazilu and Ștefania Constantinescu*

Assistant Professor, PhD, Technical University of Civil Engineering, Romania

Submission: June 21, 2023; Published: June 28, 2023

*Corresponding Author: Ștefania Constantinescu, Assistant Professor, PhD, Technical University of Civil Engineering, Romania

How to cite this article: Ion Mierluș-M, Ștefania C. Some Mechanical Equilibrium Problems. A Geometrical Point of View. Civil Eng Res J. 2023; 14(1): 555876. DOI 10.19080/CERJ.2023.14.555876

Abstract

In this paper we give a geometrical solution for a mechanical equilibrium problem, namely for a bar that is hung by 2 threads from a fixed point. Despite the fact that most of the engineering modelling problems are solved using Mathematical Analysis, we will reduce the solution of our problem to determining the coordinates of a certain point in the Cartesian coordinate system. More, we will find the value of the forces appearing in the threads. Some generalizations are provided. The mechanical notions are minimal and they will be mentioned at first and some very simple geometric results, such as bisectrix theorem, law of cosines, the congruence of the angles will be used all along the paper. The forces that are not taken into account in the problem are considered negligible.

Keywords: Mechanical Equilibrium Point; Congruent Angles; Bisectrix

Introduction

Mathematical analysis is an essential component of the scientific culture of any natural researcher, because, along with the informational aspect, it develops calculation skills, (each main theorem being related to numerical evaluations) offering many examples of mathematical modeling of some engineering phenomena; it permanently extended its study object by developing new concepts. In correlation with modern computing techniques, it solved problems that were inaccessible until recently. It remained a fundamental discipline for technical education and a scientific field with numerous ramifications. The proof of the majority of engineering principles is outlined by derivatives, integrals - real indicators for describing many developments over time. It is a relatively modern discipline having its origin only in the XVIIth century, following developments such as those of I. Newton, Leibniz and Pierre de Fermat in the calculus area.

But mathematical analysis could not have been built if Geometry and Arithmetic had not existed before. Geometry and Arithmetic represent the oldest “mathematical sciences” having their origin more than 2500 years ago, when the Egyptians had already known that the triangle with 3,4,5 units of length is right and the Greeks had various experimental discoveries that they synthesized in theorems and demonstrations. We owe Euclid the treatise “Elements”, where results regarding sizes, similarity of triangles, quadrilaterals, circles are synthesized. The one who first combined mathematics and physics was Archimedes, discovering the law of levers and the law of floating bodies, unifying Geometry and Mechanics and opening the “game with infinity”. For more details, one can consult [1-5], etc. Using the model of the great Archimedes, in this work we will solve a problem of mechanical balance, simultaneously involving Euclidean geometry, trigonometry and analytical geometry.

Preliminary Notions

In this section we present some preliminary notions and results of mechanics and geometry that will be used all along the paper.

Preliminary Notions of Mechanics

Theorem 1. (Second Newton’s Law of Motion). The change of motion of an object is proportional to the force impressed and it is made in the direction of the straight line in which the force is impressed.

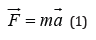
Remark 1. An equilibrium condition is given by, hence

For much information about the mechanical notions above one can consult [2-5].

Preliminary Notions of Geometry

Theorem 2. (law of cosines) Using Figure 1 the law of cosines states:

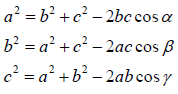
Theorem 2. (theorem of bisector) In a triangle ΔABC , the bisector of angle determines on the opposite side (BC) segments proportional to the sides of the angle (Figure 2):

Theorem 3. Vertically opposite angles are congruent (Figure 3).

Theorem 4. In a rhombus the opposite angles are congruent (Figure 4).

For much information about the geometry notions above one can consult [1].

A Mechanical Equilibrium Problem

This section represents the main part of the paper, presenting a mechanical equilibrium problems: ”the pendulum” whose solution will be given using geometrical technics.

The ”pendulum”

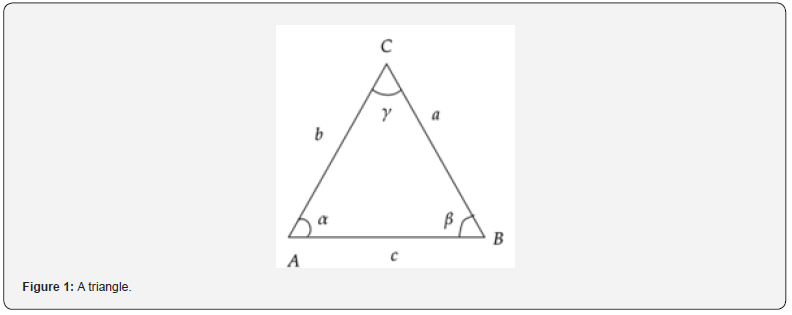
We consider a non-homogeneous bar AB , of length l . The bar is in equilibrium, having its ends tied by an inextensible thread, flexible, without weight, of length L , which passes, without friction through a fixed point , located outside the bar. Find the equilibrium position of the bar and the magnitude of the binding forces (the tension forces), knowing that the tension forces are applied in the points A and B , having equal magnitudes, and the position of the center of gravity is given by point D, which divides the bar into the ratio.

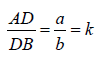
Conditions regarding the existence of the solution

We have given a solution for our problem, but know we have to answer at the following question: is it possible that the equilibrium point does not exist? We have started the solution of the problem by imposing some mechanical conditions of equilibrium and we have reached to some results in a trigonometric form. Of course, the conditions regarding the existence of the equilibrium point must satisfy the existence of the cosine cos 2β of and of the triangle ΔAOB .

A Generalization

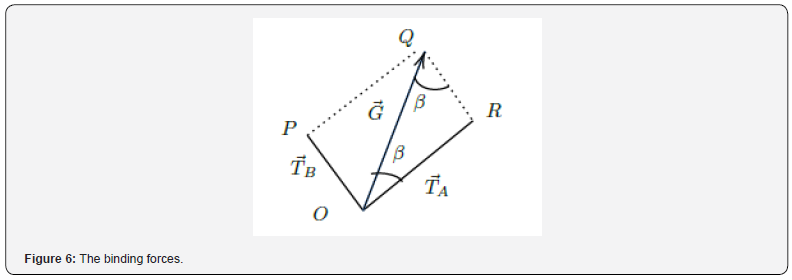
Remark 6. It is well known that the geometric image of a cartesian product of two intervals 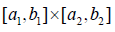(supposing 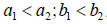, but it is not necessarily) represents a rectangle of sides , of three intervals ΔDOB is a rectangular parallelepiped a.s.o. It can be generalized to a cartesian product of a finite number of intervals obtaining an n-dimensional rectangle (Figure 7).

The problem from section 3 presented a bar having only length, i.e. it was a 1-dimensional problem. A certain generalization would be to consider a bar having area, i.e. a 2-dimensional bar, which means that the bar becomes a rectangular plate. The plate would be hung by 4 threads and can be considered 2 cases: an homogenous plate and a non-homogenous plate (case where the position of the center of mass is given). The homogenous plate case can be easily treated in the same way as the problem presented in section 3 dividing it in two 1-dimensional bars (i.e. DB and AC ), with a common gravity center. As the plate is homogenous, its gravity center will be at the intersection of them (Figure 8). In case of a non-homogenous plate, we need to equivalate the plate to two non-homogenous bars such that the gravity center of the plate will concide with the gravity center of the system of bars. This think is possible (Figure 9).

Conclusion

In the future we propose to solve the generalization of the problem for a rectangular parallelepiped case, i.e. an empty of filled box homogenous or non-homogenous.

References

1. Berger M (2009) Geometry i, Springer Science & Business Media.
2. Cleja-Țigoiu S, Țigoiu V (2017) Reologie, Editura Universităţii din Bucureşti, Romania
3. Dragoș L (1976) Principiile mecanicii analitice, Editura Tehnică.
4. Hill TL (2013) Statistical mechanics: principles and selected applications, Courier Corporation.
5. Reddy JN (2017) Energy principles and variational methods in applied mechanics, John Wiley & Sons.