Research Article

Mixing of Granular Media-Calculation of Stress at the Blade Front

Štefan Gužela*, Marián Peciar and František Dzianik

Institute of Process Engineering, Faculty of Mechanical Engineering, Slovak University of Technology in Bratislava, Slovak Republic

Submission: June 26, 2021; Published: July 20, 2021

*Corresponding Author: Štefan Gužela, Institute of Process Engineering, Faculty of Mechanical Engineering, Slovak University of Technology in Bratislava, Námestie slobody 17,812 31 Bratislava, Slovak Republic

How to cite this article: Štefan G, Marián P, František D. Mixing of Granular Media-Calculation of Stress at the Blade Front. Civil Eng Res J. 2021; 12(1): 555826. DOI 10.19080/CERJ.2021.12.555826

Abstract

Particulate materials are processed in various machines and equipment where it needs to ensure a motion of machines parts in a form of the flat blade through a layer of the grainy material. Conveyers, feeders, driers and especially mixers of granular materials can be mentioned as examples. Markedly, mixing elements of various sizes and shapes are moved through a bed of the granular material that resists this movement. Knowledge of interaction between the granular material and element moving through a bed of the granular media is necessary for the regular design and calculation of such machines. The paper deals with exact determination of force effects of the mixed material on moving blade submerged in a grain material. The solution is based on a yield equilibrium tensions of the particulate material described by theory of Mohr’s circle. A box in form of rectangular prism will be used in experiments which enables uniform rectilinear motion of the blending elements of a simple design.

Keywords: Mohr’s circle; Rectilinear motion of blade; Homogenizer; Particulate material; Yield equilibrium; Failure zone

Introduction

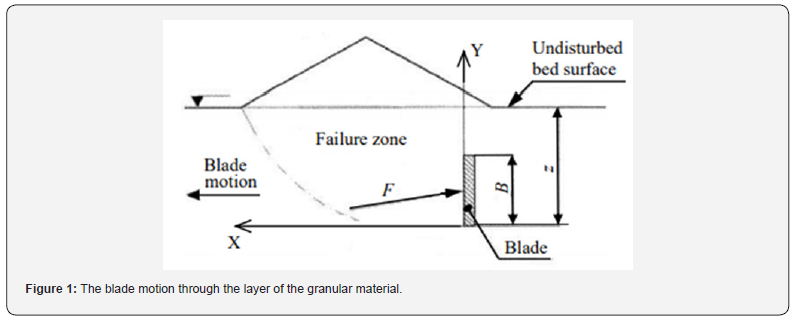
Mixing is wide-spread process in the various branches of industry. For example, in the chemical, food, and pharmacy industry, in the agriculture, or energetics. The special case of blending is mixing of the systems consisting of rigid particles. Mixing elements, various of sizes and shapes, are transferred through a bed of the grainy material. Knowledge of interaction between the grainy material and moving object is necessary for a construction of such machines. However, a theoretical knowledge of this problem is only little analyzed. Target of the paper is to give a theoretical and experimental basis for study of the grainy material motion in such cases. Designed experimental equipment enables to measure a force vector if grainy material acts against displacement of the blade. It makes possible to observe formation of failure zone of the particulate material in front of the moving blade. Steady state motion of the grainy material over a wide flat blade was studied in work [1]. Blade of the rectangular shape moves with constant velocity in horizontal direction through layer of the particulate material. Target of research is to explain the action of force of the granular medium on the flat blade moving through the granular medium layer. Normal of the blade can be deviationed from direction of its motion.

Theoretical Analysis

Valorization results of hitherto performed investigation

Some authors attempted to describe the energetical aspect of mixing process according to relations well-known in hydrodynamics. The authors looked for analogy between flow off a solid body by liquid and the movement of the mixing element through the layer of particulate material [2-4] or mixing of the particulate materials and mixing of liquids [5,6]. However, these efforts were mostly marked by big errors due to inadequate simplification of mechanics laws of the particulate materials. It was confirmed in these works that it is not possible to continue this way. For estimation of energetical aspect of the particulate material mixing it is necessary to start with tension state of the particulate material. It is possible to find several research works in literature dealing with these problems. Their authors base the solution of the energetical aspect of the mixing process on the tension state of the particulate materials [7-15]. They used a simple geometric models in their experiments which made it possible to solve action of force between the grainy material and the mixing element in two-dimensional problem. Derived functions, containing an influence of internal and external angles of friction of the particulate material, are complicated also for design of the mixing elements of simply form. Their determination assumes that the material is in the yield equilibrium. This state may be described by the theory of Mohr’s circle. Based on the works mentioned above, it is possible to draw several conclusions. Region of the failure zone forms in front of the moving blade through a layer of the granular media (Figure 1). A course of the slip lines is possible to determine by the theory of Mohr’s circle in this region. Then, a force acting on the blade can be estimated by form of the slip lines. This force is very important for calculation of the blender input power. The force acting on the blade depends on the form and the size of the plastic zone. The form and the size of the failure zone depends especially on mechanical-physical properties of the grainy material (namely on internal (ϕ_i) and external (ϕ) angles of friction of the particulate material), geometric dimensions of the blade and depth of the blade immersion (z) in a batch. In these works, it was investigated that bulk density(ρ_s) , internal (ϕ_i) and external (ϕ) angles of the friction of the particulate material belong among the most important parameters characterizing grainy material. Theoretical studies and experimental results proved that the internal (ϕ_i) and external (ϕ) angles of the friction are at movement of the granular media markedly assert, and hence it is not possible to ignore them, which is declared by some authors.

Analytical calculation of a stress acting on the blade

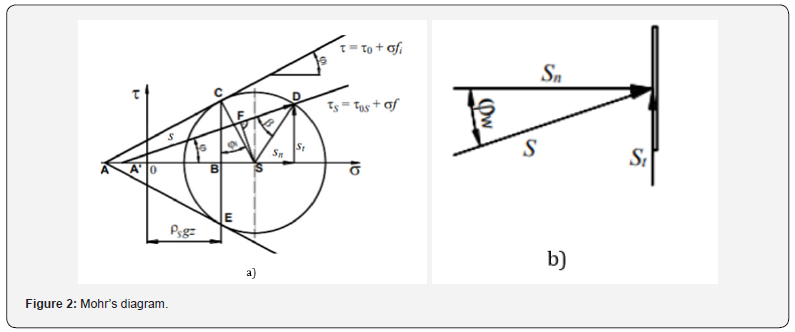
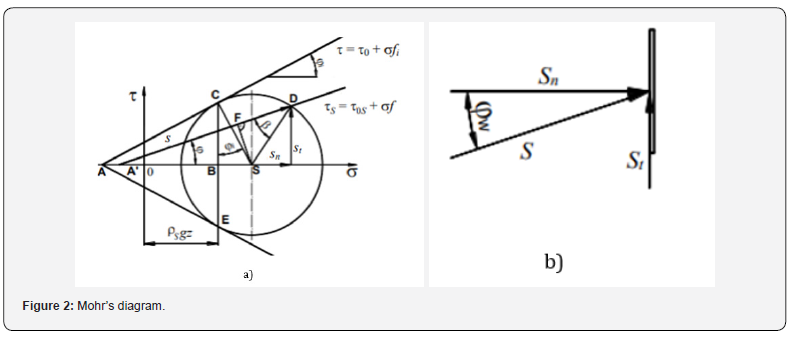
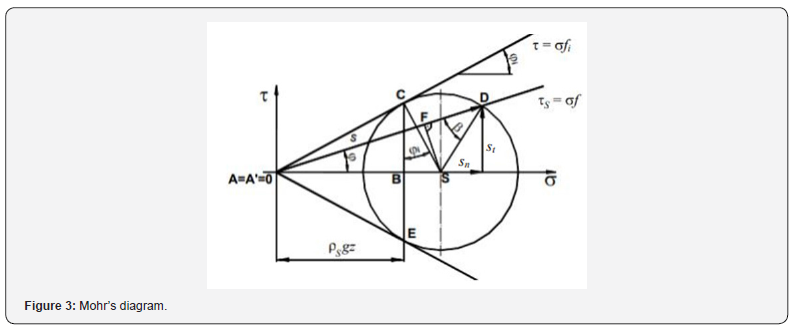
Theoretical determination of the stress acting on blade was performed for a following case. The blade of rectangular shape is situated so that its shorter edge(B) is vertical and perpendicular to a horizontal plane (Figure 1). The blade width(L) is considerably bigger than its height (B) . Problem is to define a relationship for calculation of the normal stress component(sⁿ) acting on the blade front (Figure 2) (Figure 2b). The stress distribution between the mixing element and cohesion particulate material is simply plotted by Mohr’s circle (Figure 2a). In this case the circle is Mohr’s circle of stresses, the straight-line OS is an axis of normal stresses σ and the straight line, perpendicular to the line OS and passing through point O, is the axis of tangential stresses τ.

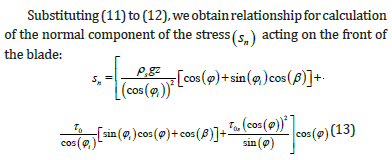
These relationships were derived for the cohesion particulate material and for the adhesive forces between the particulate material and the surface of the blade which is not possible to neglect. Let’s to consider a case where 0 τ = 0and 0 0 s τ = (Figure 3). It is cohesionless particulate material where between the particulate material and the surface of the blade are only the friction bonds. Then the relationships (6) and (13) will be simplified into the form of the relations (14) and (15). The relationship for calculation of the angle β will be:

Influence of the angle of blade inclination

The relationship (13) was derived for the rectilinear motion of the blade. Shorter edge of the blade was perpendicular to direction of its motion and a plastic zone was formed in front of the blade (Figure 5). The shape and size of plastic zone significantly affects the force acting on moving blade through layer of particulate material. Shear zone in front of the blade (Figure 6) rises with angles of internal friction (ϕ_i) and external friction(ϕ) . The influence of the angle of internal friction (ϕ_i) is possible to follow in (Figures. 6 (a, b, c)) at constant value of the angle of external friction(ϕ) . The angle of internal friction(ϕ_i influences the angle at which the slip lines are intersecting. A region of the shear zone rises with the angle of internal friction (ϕ_i) . The angle of external friction(ϕ) influences the Rankins zone shape and also additional regions. The region of shear zone rises again with the angle of external friction(ϕ) (Figures. 6 (d, e, f)).

The influence of angle of the blade inclination(α) towards the horizontal plane (Figure 7) on forming of the shear zone is also significant. Inclination of the blade normal towards a vector of its motion is changed with variation of the angle of blade inclination. As well as the angle of external friction(ϕ) could be the significant parameter affecting mutual action of the blade and the granular material. All regions of the shear zone are changing (Figure 8) with gradual rising value of the blade inclination(α) . It follows that the force needed for move of the blade through a layer of the granular material must also change. We will try to explain this fact.

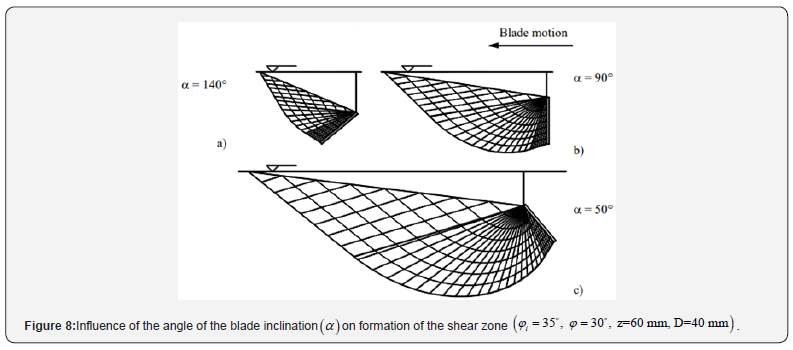
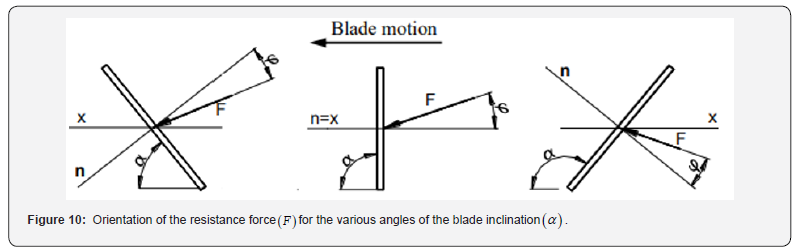
The value of the normal stress component s_n acting on front of the blade can be calculated by relationship (13). On the basis of experimental measurements, it was obtained that magnitude of the horizontal component of the force(H ) decreases with increasing value of angle of the blade inclination(α) at the constant height of the blade in projection(B) (Figure 9). This means that when the blade is inclined under the angleα < 90^o , then the value of the horizontal force (H(_α>90)) is bigger than the value of the force(H(_α=90)) . On the contrary, when the blade is inclined under the angleα > 90^o, then the value of the horizontal force (H ( _{α > 90} )) is smaller than the value of the force(H) for α = 90^o . Generally, it is possible to suppose that total force (F) is diverted from the normal of the blade by external angle of the friction(ϕ) . For various angles of the blade inclination(α) it is necessary to consider an orientation of the total force(F ) acting on the blade. Orientation of the resistance force(F), as is plotted in (Figure 10), was determined by experimental measurements [1]. The horizontal force(H ) , or (H( _{α <90} )), or (H ( _{α > 90} )), necessary to the movement of the blade through the granular material, was estimated by the resistance force(F) (Figure 10).

Value of the stress sⁿ is calculated by the relationship (13). The horizontal component of the force (H) acting on the blade plate with length L and height B for the case of α = 90^o is calculated by the value of the stress sⁿ :

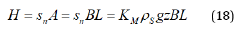
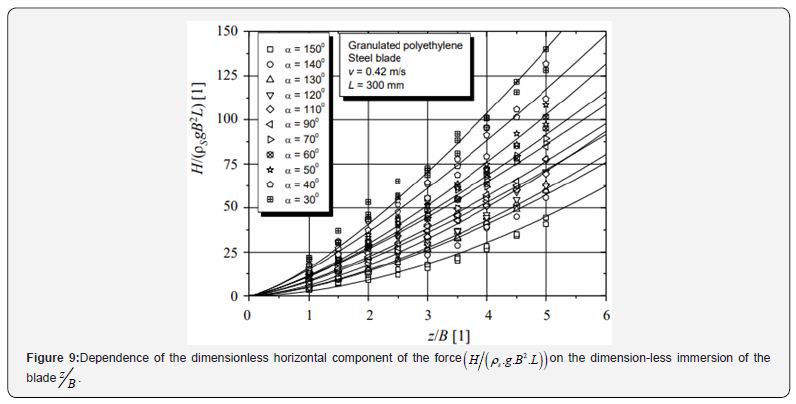
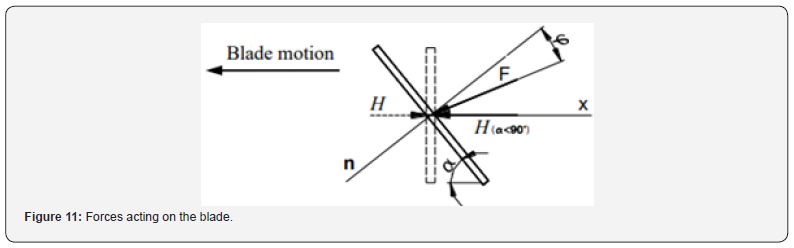
From the balances of the forces (Figure 11) in direction of the blade normal, the following is valid:

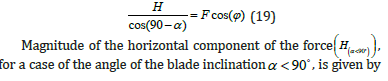
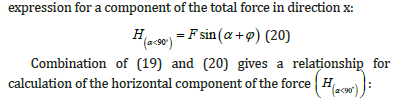
Conclusion

The introduction of article deals with available results of the investigation, from those some conclusions were deduced. It was confirmed that for calculation of the energetical aspect of the grainy material mixing it is needed to start from tension state of the particulate material. The bulk density, internal and external angles of the material friction, geometric dimensions of the blade, and depth of the blade immersion belong among the most important parameters characterizing the grainy matters which have an influence on the magnitude of the horizontal component of the force acting on the blade. On the basis of these information’s, in this paper, the relationship including the influence of these above-mentioned parameters, was designed. It is written in the part of analytical calculation of the stress acting on the blade. Next part of the article considers the influence of the blade inclination angle on the form and largeness of the shear zone in front of the moving blade, which significantly affects the magnitude of the force acting on the moving blade through the layer of the particular matters. The given relationship specifies theoretical value of the horizontal component of the force. If this relationship would give a total value of the force horizontal component, so then a ratio of the measured and theoretically calculated values would be close to one. If this ratio differs significantly from the value 1, then a computing model will be dependent on another, so far the unknown parameters. These ideal results will be the basis for formation of the dimensionless arguments by dimensional analysis of the homogenization process. Design of the criterion dependency for the calculation of the dimensionless horizontal component of the force acting on the blending element of the various form and for different types of the grainy material will be main goal of the next research. Knowledge of real force interaction between homogenized material and mixing element facilitates qualified design of the homogenizer drive.

Nomenclature

References

1. Gužela Š (2003) The Contribution to Solution of Energetical Aspect of Particulate Material Mixing. Department of Chemical Machines and Equipment, Faculty of Mechanical Engineering, Slovak republic, Bratislava p: 113.
2. Peciar M (1991) Mixing of Particulate Materials. Department of Chemical Machines and Equipment, Faculty of Mechanical Engineering, Slovak republic, Bratislava pp: 128.
3. Ruzbehi M (1982) Studies on the influence of bulk material sizes in the mixing process. Kand. dizertač. práca, University of Stuttgart, Institute for Mechanical Process Engineering, Stuttgart pp: 104.
4. Ruzbehi M, Alt Ch, Lücker R (1982) Investigations into the influence of bulk material sizes in the mixing process. Processing technology pp: 316-326.
5. Müller W (1967) Investigations on powder mixing. Chemical engineering technology 14: 851-858.
6. Pahl MH (1984) Fundamentals of Solids Mixing. Technical Notes pp: 541-551.
7. Bagster DF (1969-1970) The Prediction of the Force Needed to Move Blades through a Bed of Cohesionless Granules. Powder Technology 3(1): 153-162.
8. Bagster DF, Bridgwater J (1969-1970) The Flow of Granular Material over a Moving Blade. Powder Technology 323-338.
9. Bagster DF, Bridgwater J (1967) The Measurement of the Force Needed to Move Blades Through a Bed of Cohesionless Granules. Powder Technology 189-198.
10. Bridgwater J, Bagster DF, Chen SF, Hallam JH (1968) Geometric and Dynamic Similarity in Particle Mixing. Powder Technology 198-206.
11. Gužela Š (2000) energetical aspects of particulate material mixing. Department of chemical machines and equipment, faculty of Mechanical Engineering, Slovak republic, Bratislava.
12. Kravárik K (1994) Energetical Aspects of Particulate Material Mixing. Department of Chemical Machines and Equipment, Faculty of Mechanical Engineering, Slovak republic, Bratislava.
13. Kravárik K (1999) Energetical Aspects of Particulate Material Mixing. Department of Chemical Machines and Equipment, Faculty of Mechanical Engineering, Slovak republic, Bratislava p: 149.
14. Novosad J (1962) Mixing of Granular Material by Mechanical Blender. Institute for VPCH Czechoslovak republic, Praha pp: 199.
15. Novosad J (1963) Studies on Granular Materials I Kinematics of Granular Materials Mixed by a Mechanical Impeller. Czechoslovak Academy of Sciences, Prague pp: 2681-2696.