- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Should Companies Invest in Sustainability?
Jiang Jun Lee1* and James M Kelly2
1 Technology and Engineering Division, Malaysian Rubber Board, Malaysia
2Department of Civil and Environmental Engineering, University of California, Berkeley
Submission: February 23, 2019; Published: March 15, 2019
*Corresponding Author:Yossi Sheffi, MIT Center for Transportation and Logistics, USA
How to cite this article:Jiang J L, James M K. The Effect of Damping in the Isolation System to the Response of the Structure. Civil Eng Res J. 2019; 7(4): 555718. DOI: 10.19080/CERJ.2019.07.555718
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Research Article
The technique of using base isolation system to protect the structure and the contents of the structure has been proven effective in past earthquakes. Modelling of base-isolated structure is crucial to ensure that the response is predicted correctly. In this study, the linear viscous damper was used to represent the energy dissipation mechanism to study the effect of damping in the isolation system to the response of the structure. The peak isolator displacement, peak interstory drift and the roof floor acceleration response spectrum were used to evaluate and compare the effectiveness of the isolation system. Other variables in this study were the period separation and the level of damping in the isolation system. The use of bilinear model to model base-isolated structure is common due to the simplicity of the model and the ease to implement in computing software. However, the simplicity of the bilinear model has also restricted the ability to define the mechanical properties of the model over a wide range of shear strain. This study found that some degree of damping in the isolation system is beneficial to the structure but when the damping is too high, the key objective of isolating the structure-to protect the contents of the structure-is hampered due to the presence of high frequency vibration.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Introduction
Base isolation technique is one of the methods to mitigate the effect of earthquakes to structures, but this is the only technique among others that can protect both the structure and the contents of the structure from the ground shaking. Base isolation can be achieved through various approaches, such as the use of high damping elastomeric bearings, lead rubber bearings and friction pendulum bearings. A hybrid system can be created by combining two of more isolation mechanisms or by introducing additional damper system to increase the energy dissipation capability. The fundamental of this technique lies in the concept of lengthening of the fundamental period of the structure such that the natural period of the system does not fall in the range of the predominant period of the earthquakes [1]. The base isolation technique is widely used around the world, including the United States, Armenia, Chile, China, Indonesia, New Zealand, and particularly Japan [2]. Damping is the most critical property for a system responding at resonance, such as base-isolated system. Damping plays a role in controlling the dynamic response of the system and reduces the peak displacement demand at resonance. In structural dynamics, the linear viscous damper model is very often used to represent the energy dissipation mechanism. Bilinear model is one of the most well-known mathematical model to model hysteresis or energy dissipation. This model is simple and easy to implement in computer software. Despite the model has energy dissipation feature, the energy dissipation mechanism varies with material. In addition, due to the simplicity of the model, the mechanical properties of the model are correct at the calibration shear strain but can quickly deviate from the actual properties of the material if the energy dissipation mechanism of the material and the bilinear model is different.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Earthquake Protection of Structures
Earthquake protection of structures has been an ongoing effort and over the years, many technologies and techniques have been developed. At the same time, most of these technologies and techniques have been tested by real earthquakes. Base isolation is one of the technologies that can be used not only to protect the structure but the contents of the structure from earthquake shaking. Base isolation can be achieved by introducing an isolation system between the superstructure and the substructure. The isolation system alters the dynamic properties of the structural system. This alteration leads to a fundamental mode of the system whereby the superstructure acts like a rigid body while the deformation is mainly in the isolation system. Some of the commonly used components to isolate a structure are elastomeric bearings and friction pendulum bearings. In addition to installing bearings as an isolation system, additional components are sometimes introduced to the isolation system such as dampers to dissipate energy and to control the response of the superstructure [3].
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Bilinear Model
Bilinear model is a highly simplified mathematical model to represent an element with restoring force and energy dissipation capabilities. This model has been widely used due to the simplicity both in the concept and the implementation in computer modelling. When a bilinear model is subjected to sinusoidal input of amplitude D, the peak displacements are represented by D− and D+ , the minimum and maximum peak displacement respectively, and the minimum and maximum forces correspond to the minimum and maximum peak displacements are F− and F+ respectively. The force value when the hysteresis loop crosses the vertical axis is called the characteristic force, Q. In addition, the hysteresis loop of a bilinear model has two stiffnesses, the initial stiffness, and the second stiffness, K2. The graphical representation of the bilinear model and the parameters are shown in Figure 1.
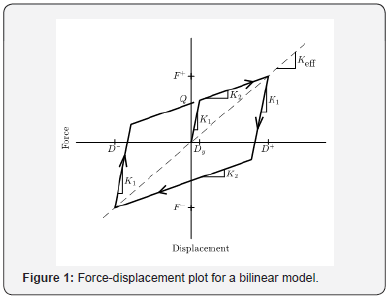
Nonetheless, only four basic parameters are required to properly define a bilinear model, i.e., the initial stiffness, K1, second stiffness, K2 and the characteristic strength, Q and the yield displacement, Dy . Therefore, the mechanical properties of the bilinear model can be defined using these basic parameters.
Another key parameter of the bilinear model is the effective stiffness, eff K , defined by Equation (1).
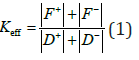
With the mass of the system known, the effective stiffness is used as a proxy to estimate the effective period of the system. The effective stiffness of the system, in terms of the basic parameters of the bilinear model is shown in Equation (2).
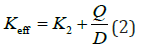
In addition, the effective damping ratio of the system, eff β , for the displacement amplitude D is shown in Equation (3).
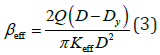
In is evident from Equations (2) and (3) that both the effective stiffness and effective damping ratio of the bilinear model is displacement dependent.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Structural Model
In order to evaluate the effectiveness of the isolation system, a single-degree-of-freedom (SDOF) system was extended to a twodegree- of-freedom (2DOF) base-isolated system. The SDOF system consists of one lumped mass, ms , that represents the mass of the superstructure, and is supported by a massless column with stiffness coefficient, ks and damping coefficient, cs (Figure 2). The damping in the superstructure was assumed to be represented by a linear viscous damper model where the damper force is proportional to the relative velocity of the system. The fixed-base SDOF system used in this study is assumed to have a period of 0.4sec. The 2DOF base-isolated model is an extension of the SDOF model shown in Figure 2. The 2DOF base-isolated system consists of one additional mass, mb , that represents the base mass and the restoring force in the isolation system is defined as fb (Figure 3). The detailed explanation of this approach is available in the book Earthquake-Resistant Design using Rubber by Kelly [4].
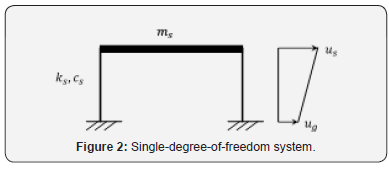

The absolute displacement of the ground, base mass, b m , and the superstructure mass, ms , are represented by ug , ub and us respectively. Two isolator models were considered in this study, namely the linear spring with linear viscous damper model and the bilinear isolator model. Although the mechanical properties of the former are unlikely to be true in practical use since almost all isolators have some degree of nonlinearity, but the response can be linearized in some form such that the analysis and computation can be simplified. In addition, the linear viscous damper model is commonly used in structural analysis to represent the energy dissipation mechanism in a structure [5]. For the linear viscous damper model, the isolator restoring force can be written in the form shown in Equation (4).
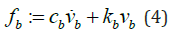
where b c and b k are the linear viscous damper coefficient and linear stiffness coefficient of the isolator model, and b v and b v are the relative velocity and relative displacement of the base mass respectively. The relative displacements of the masses are defined as vb:=ub-ug and vs:=us-ub For the bilinear model, the restoring force depends on the loading and unloading path on the hysteresis loop (Figure 1). Another form of energy dissipation mechanism is the hysteretic damping. This energy dissipation model requires solving for the response of the structure in the frequency domain. This will further increase the complexity of the problem [6,7].
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Equation of Motion
By taking the section cuts through the columns and the isolation system and equating the inertia force experienced by the masses to the restoring force, the equations of motion can be established. The relative displacements for the masses in terms of the absolute displacements are :s vs:=us-ub and vb:=ub-ug for the superstructure mass and base mass respectively
The equations of motion obtained from the section cut are shown in Equations (5) and (6).
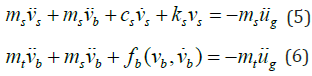
where mt is the isolated mass, mt := ms + mb .
The equations of motion for the system can be further transformed into the form of matrix equation of motion. The matrix equation of motion for the system with linear spring and linear viscous damper isolation system is shown in Equation (7) while the equation of motion for the system with bilinear isolation model is shown in Equation (8).
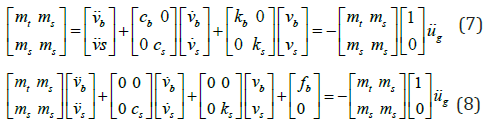
The matrix form equation of motion shown in Equations (7) and (8) can be solved numerically using mathematical tools such as Matlab. Before the second order matrix ordinary differential equation is solved, the system was transformed into a system of first order differential equations. The built-in toolbox, ode45 in Matlab, was used to solve for the response.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Floor Response Spectrum
Response spectrum is a representation of the peak response of a series of linear SDOF systems with different periods subjected to the same excitation. The floor response spectrum is a record of peak response of linear SDOF systems subjected to the acceleration experienced by the mass where the SDOF systems are placed on. This approach can be a useful proxy for the performance of a piece of equipment placed on a certain floor within a superstructure that does not interact with the dynamic response of the superstructure during an earthquake.
In this study, the floor response spectrum is used to study the effectiveness of the isolation system. One of the objectives of isolating a structure is to also protect the contents of the structure. Hence, if the floor response spectra for the floor masses within the isolated structure indicate that the peak responses are mainly around the nominal isolation period, then the isolation system has successfully protected the contents of the structure from high frequency vibration. However, if peak responses are observed to be present at shorter period (higher frequency) region relative to the nominal isolation period, higher modes response might have excited. Based on conventional modal analysis in structural dynamics, the modal period decreases with increasing mode; therefore, when higher modes response is excited, high frequency (short period) vibration will be present within the superstructure; equipment that is sensitive to high frequency vibration might be damaged. The steps in generating a generic floor response spectrum are shown in Figure 4.
The equipment with mass m is placed on the upper floor of a two-degree-of-freedom (2DOF) system. The mass of the equipment is assumed to be very small relative to the floor masses ( ms m and b m m ) and does not have significant contribution to the dynamic response of the superstructure. The response of the 2DOF system with masses ms and ms was obtained by solving the equation of motion (Equation (8)) numerically using the ground motion recording as an input.
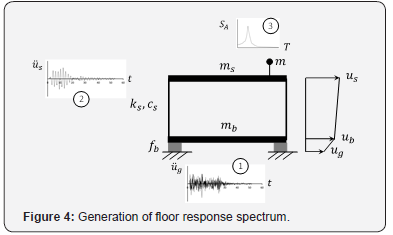
The absolute acceleration for the floor mass, s u , where the equipment is placed is obtained.
The response of the mass m is obtained by solving the equation of motion using the floor acceleration from 2 as the input. Step 3 is repeated for the SDOF system of mass m with various periods and the peak response is plotted against the natural period to generate the floor response spectrum.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Ground Motion Selection
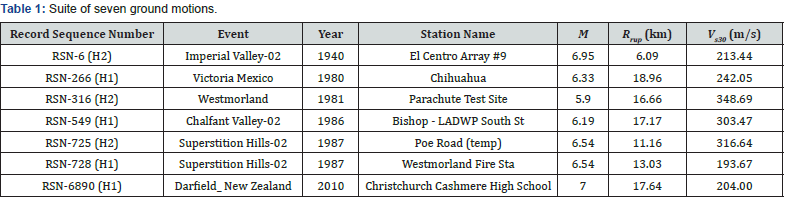
In this study, an arbitrary site located at 37.78 °N, 122.39 °W, with Class D (stiff soil) soil type was selected. A suite of ground motions was selected from the Ground Motion Selection Database on the Pacific Earthquake Engineering Research Center (PEER) website. The design spectrum for the site was established according to the procedure outlined in the ASCE 7-16 design document [2].
A suite of seven ground motions that has magnitude, M between 5 and 7, and rupture distance, rup R between 0-20km and matches the above site condition was selected using the Ground Motion Selection Database by PEER. The details of the suite of ground motions are summarized in Table 1.
Linear Spring and Linear Viscous Damper Isolation System
The first study on the effect of damping in the isolation system was carried out using the 2DOF base-isolated structural model with linear spring and linear viscous damper isolator. The fixedbase frequency, s ω , is defined as
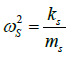
while the nominal isolation frequency b ω , is defined as
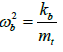
These two frequencies are assumed to be well separated. The ratio of these frequencies, ε, is defined as
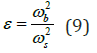
For systems with well separated frequencies, is assumed to be in the order of between 10−1and 10−2 . The damping ratios of the structure and the isolation system, and , are
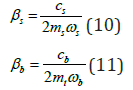
Both damping ratios of the structure and the isolation system are of the magnitude of .
The dynamic properties of the base-isolated structure were obtained by solving the eigenproblem for Equation (7). The modal frequencies, expressed in terms of the SDOF structural frequencies and the nominal isolation frequencies are
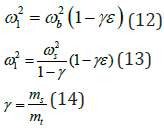
For cases where the fixed-base and isolated frequencies are
well separated, the modal frequencies of the base-isolated system
can be approximated to  . It can be observed
that the first mode period is the nominal isolation period,
i.e. the superstructure behaves and responds like a rigid body
and the displacement is only taking place in the isolation system;
whereas in the second mode, as the mass ratio, γ, is always less
than unity, the vibration frequency is increased slightly as compared
to the fixed-base frequency.
. It can be observed
that the first mode period is the nominal isolation period,
i.e. the superstructure behaves and responds like a rigid body
and the displacement is only taking place in the isolation system;
whereas in the second mode, as the mass ratio, γ, is always less
than unity, the vibration frequency is increased slightly as compared
to the fixed-base frequency.
The mode shapes obtained from the eigen analysis, where the eigenvector for the base mass is assumed to be unity, are
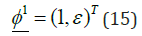
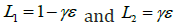
The graphical representation of the mode shapes is shown in Figure 5.

The mode shape for the first mode response agrees with the
modal frequency interpretation where the deformation is mainly
in the isolation system and deformation in the superstructure is
only of the order ε. However, the mode shape for the second mode
indicated that the deformation is mainly in the superstructure,
which is a less desired response as this defeat one of the objectives
in isolation a structure, i.e., to protect the contents of the structure.
Using the information from the mode shapes, the participation
factors for the system are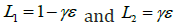 and the effective
modal masses are
and the effective
modal masses are 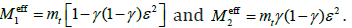
Considering these terms to the zeroth order of ε, i.e., the frequencies are well separated, the second mode does not contribute to the overall response of the structure. In other words, the second mode response is almost orthogonal to the earthquake input and should there be any energy in the earthquake input at this frequency, the energy will not be transmitted into the superstructure. Therefore, these results indicated that the effectiveness of the isolation system depends on the period separation and more importantly, the isolation system works by deflecting the energy through orthogonality in the dynamics of the structure and the earthquake, and not by absorbing the energy of the earthquake. However, energy dissipation mechanism still has an important role in an isolation system
Further investigating into the modal damping ratios for each mode shows that
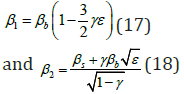
The damping ratio for the first mode, 1 β is a slight modification of the damping ratio of the isolation system by the product of the mass ratio and the frequency separation. However, the second mode damping ratio, 2 β is influenced by the damping ratio in the superstructure and the damping ratio in the isolation system. If the damping ratio in the superstructure is small relative to the damping ratio in the isolation system, the product of b β and ε could cause the second term in Equation (18) to be the governing term for this expression.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Normalized Bilinear Model
In order to be able to work independently of the geometry of the isolator, the mechanical properties of the bilinear model were normalized by the area of the isolator, A. In addition, the pressure exerts on the isolator, p is assumed to be 1000psi. Hence, the effective stiffness, eff K and effective damping ratio, eff β of the bilinear model shown in Equations (2) and (3) are normalized and modified to the form shown in Equations (19) and (20) for the normalized effective stiffness, Keff and βeffrespectively.
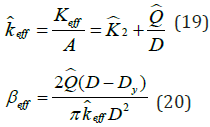
where K is the normalized second stiffness and Q is the normalized characteristic strength. The expression for the effective stiffness can be further written in terms of the properties of the isolator and the dynamic properties of the system, i.e., the pressure on the isolator, p and the period correspond to the maximum displacement, M T , as shown in Equation (21).
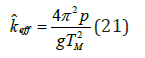
Likewise, the normalized characteristic strength, Q can be cast into the form shown in Equation (22).
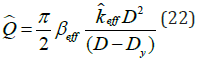
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Case Study using Linear Spring and Linear Viscous Damper Model
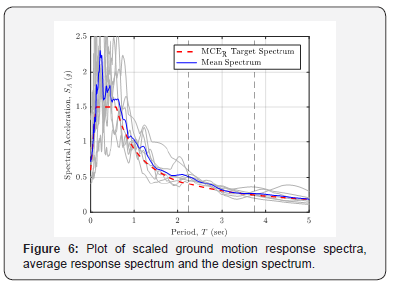
Prior to the analysis, the suite of ground motions listed in Table 1 was scaled according to the procedure outlined in the ASCE 7-16 design document [2]. The design code requires that each ground motions should be scaled to match the design spectrum within the period range of 0.75 TM and 1.25 TM , where TM is the period at the maximum displacement. In this study, TM was taken as 3sec. In addition, the average acceleration response spectrum obtained from the suite of ground motions should not be less than the design spectrum for any period over the same period range. These conditions resulted in a typical constrained linear leastsquares problem that can be solved using computational mathematical tools such as Matlab. The detailed solution to this problem is explained in Doctoral Dissertation by Lee [8]. The plot of the scaled ground motions response spectra, the average acceleration response spectrum and the target design spectrum is shown in Figure 6.
The case study on the structural model with linear spring and linear viscous damper model is carried out by varying the period separation and the damping ratio in the isolation system, as these two factors were observed to influence the response of the base-isolated system. The nominal isolation periods were chosen to be 3sec and 4sec while the damping ratio in the isolation system varied from 5% to 45%. The 2DOF base-isolated model was used in this study and the equation of motion for the system was solved numerically using Matlab with the scaled ground motion as input. The comparison on the effect of damping ratio and period separation was carried out. The peak isolator displacement and peak story drift are summarized in Table 2 and Table 3 respectively.
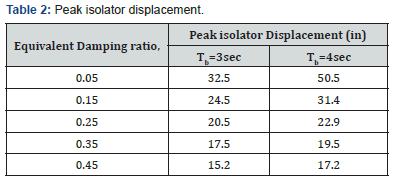
The peak isolator displacement was observed to reduce with the increasing damping ratio in the isolation system. In addition, longer nominal isolator period, Tb also resulted in larger displace ment demand. However, there is no significant difference in the peak roof drift for these cases. Besides displacement and drift, the comparison was made on the roof floor acceleration response spectra for systems with various damping ratios and period separation values. The plot of the average roof floor spectrum for a system with 3sec nominal isolation period and various damping ratios in the isolation system is shown in Figure 7.
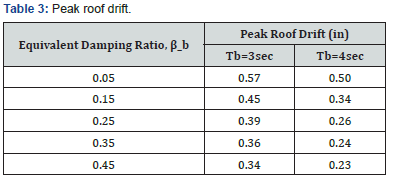
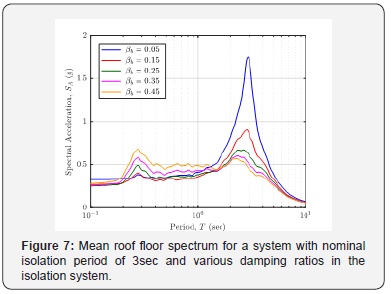
For a system with very low damping in the isolation system, i.e., 5%, the roof floor response spectrum only peaked at the nominal isolation period. However, as the damping ratio in the isolation system increases, the peak at the nominal isolation period becomes less apparent and another peak near the period of 0.3sec began to become significant. When the damping ratio in the isolation system exceeded 35%, the peak near the period of 0.3sec became the dominant peak in the roof floor response spectrum. When the peak at the shorter period appears in the roof floor response spectrum, this indicates that the vibration of the mass consists of high frequency element. In other words, there is also high frequency (low period) vibration components in the response. This type of respond is less favorable as any vibration sensitive equipment placed on this mass might be affected. The mean roof floor response spectrum for a system with nominal isolation period of 4sec and various damping ratios in the isolation system is shown in Figure 8.
Similar observation can be made on the roof floor response spectra in terms of the effect of increasing damping ratio in the isolation system for the system with 4sec nominal isolation period. For an isolation with low damping, the isolation system acts almost like a filter, allowing only energy near the first mode period to enter the structure. This shows that the isolation system is effective when the damping is low. When the damping ratio increases, the presence of high frequency vibration in the superstructure becomes more significant thus reducing the effectiveness of the isolation system. On the other hand, the larger the period separation, the lower the response spectrum ordinate of the roof floor mass. Hence, the acceleration experienced by the mass is reduced. However, the price to pay for the reduced acceleration is the increased displacement demand in the isolation system.
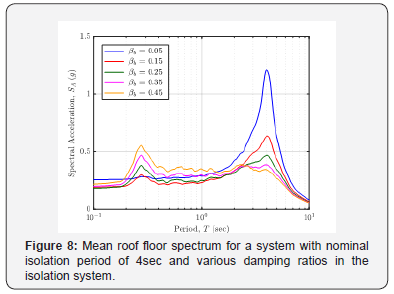
As mentioned before, the presence of high frequency component is more significant as the damping in the isolation system increases. From Figure 7 and Figure 8, it can also be observed that when the damping in the isolation system is low, the dominant peak in the roof floor acceleration response spectrum is near the nominal isolation period. As the damping increases, the peak near the second mode period, i.e. around 0.3sec, become more obvious and when the damping ratio is beyond 45%, the dominant peak in the floor acceleration response spectrum is at the second mode period region.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Case Study using Bilinear Model
The case study using bilinear model is a typical design scenario where the design shear strain was chosen as 100%, which corresponds to 40in. displacement, the damping ratio at the design shear strain was set to 10% and the target period at the design shear strain was 4sec. In addition, the design code also requires the following set of equations (corresponds to Equations 17.5-1, 17.5-2 and 17.2-3 in ASCE 7-16) that is stipulated in the code to be satisfied [2].
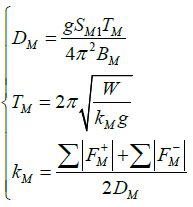
This set of equations are coupled; thus, these parameters will have to be solved iteratively. Besides, three ground motion inten sities are considered in this study, namely the service level earthquake (SLE), design basis earthquake (DBE) and maximum considered earthquake (MCER). These ground motion intensities are related where SLE is 50% of DBE and MCER is 150% of DBE. At the MCER ground motion intensity, the ground motion parameter at 1-second period, SM1 was chosen to be 1.2. By using the above correlations for different ground motion intensities, the ground motion parameter at 1-second period for 0.5DBE and DBE, SS1 and SD1 were 0.4 and 0.8 respectively.
Using Equations (21) and (22), the normalized effective stiffness, eff k and normalized characteristic strength, Q at 1.5DBE ground motion intensity are 6.4psi/in. and 41.4psi respectively. The normalized initial stiffness, k1 and normalized second stiffness, k2 are 93psi/in. and 5.4psi/in. The ratio between the second and initial stiffness, k1 / k 2 is approximately 18. This bilinear model resembles an isolation system using lead plug bearings [9].
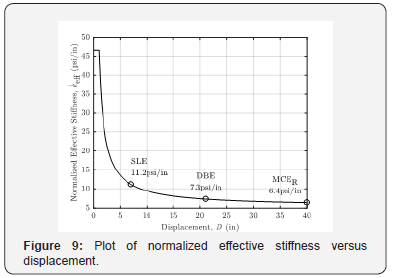
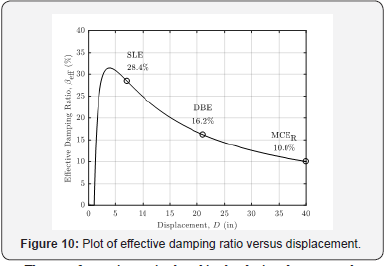
The set of equations stipulated in the design document shown above was used to determine the targeted displacement, effective period and effective stiffness of the isolation system at the SLE and DBE intensities. The maximum displacements at the SLE and DBE ground motion intensities for the system are 7.1in. and 21in. respectively. The normalized effective stiffness of the system at the SLE and DBE ground motion intensities are 11psi/in. and 7.3psi/in. while the effective damping ratios at the SLE and DBE ground motion intensities are 28% and 16% respectively. The effective periods are 3sec and 3.7sec for the SLE and DBE ground motion intensities respectively. The distribution of the effective stiffness and effective damping ratio of the bilinear model up to the displacement correspond to the design shear strain is shown in Figure 9 and Figure 10 respectively.
Prior to conducting the dynamic analysis, the suite of ground motions was scaled such that the response spectral ordinate corresponds to 1-second period matched the ordinate of the design spectrum at 1-second period, SM1, as shown in Figure 11. The equation of motion shown in Equation (8) was solved using Matlab with the scaled ground motions as the exciting force.

The matrix equation of motion for the base-isolated system was solved numerically to obtain the response of the superstructure. The absolute acceleration time series of the superstructure mass was established to be used as the input to generate the roof floor response spectrum. To further improve the efficiency of the solution, the scalar equation of motion, i.e., the equation of motion for generating the response spectrum, was solved using the closed-form solution instead of the numerical time-stepping procedure.

The roof floor response spectra for the system and the average roof floor response spectrum when subjected to the suite of ground motions scaled to the design spectrum is shown in Figure 12. The average roof floor response spectrum shows two distinct peaks, one at the period of around 4sec while the other peak is at the period of about 0.3sec. The period of 4sec corresponds to the nominal isolation period of the structure. The presence of another peak at shorter period region suggested that higher modes response has been excited or high frequency vibration has entered the superstructure. Therefore, the response of the structure could be detrimental to vibration sensitive equipment housed within the structure. In other words, the isolation system was not effective in protecting the contents of the structure from high frequency vibration.
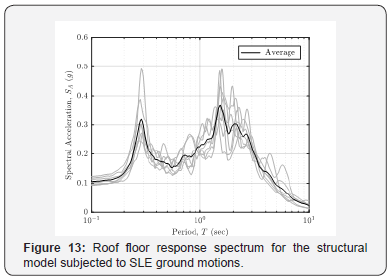
Similar procedure was carried out using the suite of ground motions scaled to the SLE and DBE intensities. The roof floor response spectra and the average roof floor response spectrum was generated and shown in Figure 13 and Figure 14 for the SLE and DBE intensity respectively.
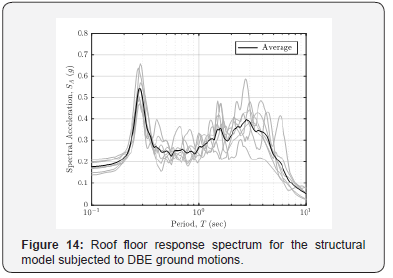
The roof floor response spectra obtained at the SLE and DBE ground motion intensities showed similar trend as the roof floor response spectrum obtained from the system subjected to the MCER ground motions. Two peaks are observed at the period around 4sec and 0.3sec. The comparison of the average roof floor response spectrum for different intensities is shown in Figure 15.
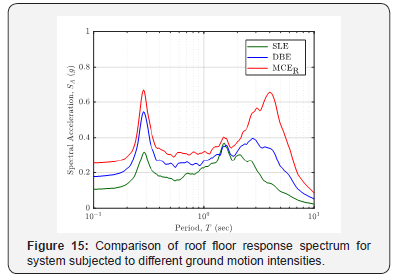
The presence of peaks at the short period region (around 0.3sec) indicated that the structural model with bilinear model, regardless of the ground motion intensity is experiencing high frequency vibration within the superstructure. In other words, the isolation system is not effective in protecting the contents of the structure, particularly vibration sensitive equipment. A comparison was made on the mean peak isolator displacement and the maximum design displacement obtained using the equation stipulated in the ASCE 7-16 design code. The observation is summarized in Table 4.
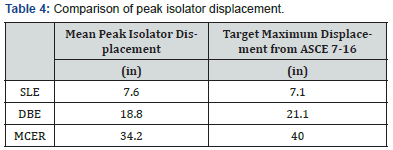
The mean peak isolator displacement obtained from a suite of seven ground motions did not deviate too much from the values estimated using the equation stipulated in the design code for various ground motion intensities.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Conclusion
Base isolation is an effective technique to mitigate earthquake damage on structures. As shown through analytical and numerical examples, the base isolation is effective when the damping ratio in the isolation system is low. Nonetheless, some level of damping in the isolation system is needed so that the design of the isolation system can be more economical and for better control of the dynamic response. Incorporating high level of damping to the isolation system may help to reduce the displacement demand but at the same time could excite high frequency response. As a result, the intention of protecting the contents of the structure might be jeopardize, particularly when the structure houses vibration sensitive equipment. The bilinear model is a popular mathematical model for structural analysis due to the simplicity and ease of implementation. However, an engineer or designer should consider the variation and deviation of the mechanical properties of the model to the actual isolation system that will be used to ensure that the superstructure and the isolation system are properly design for.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
Acknowledgement
Part of the work in this study was carried out as the research work for a Doctoral Degree awarded at the University of California, Berkeley. The doctoral study was made possible with the scholarship provided by the Malaysian Rubber Board and summer fellowship provided by the Department of Civil and Environmental Engineering, University of California, Berkeley.
- Research Article
- Abstract
- Introduction
- Earthquake Protection of Structures
- Bilinear Model
- Structural Model
- Equation of Motion
- Floor Response Spectrum
- Ground Motion Selection
- Normalized Bilinear Model
- Case Study using Linear Spring and Linear Viscous Damper Model
- Case Study using Bilinear Model
- Conclusion
- References
References
- Chopra AK (2012) Dynamics of Structures. (4th edn), Theory and Applications to Earthquake Engineering, Pearson Education Inc., Upper Saddle River, New Jersey, USA.
- American Society of Civil Engineers (2016) ASCE Standard, Reston, American Society of Civil Engineers, Virginia, USA.
- Charleson AW, Guisasola A (2015) Seismic isolation for architects. In: New Zealand Society for Earthquake Engineering (NZSEE) Conference, Rotorua, New Zealand.
- Kelly JM (1997) Earthquake-Resistant Design with Rubber, Springer- Verlag, London, England pp.1-213.
- Beards CF (1996) Structural Vibration: Analysis and Damping. John Wiley & Sons Inc, New York, USA.
- Clough RW, Penzien J (2003) Dynamics of Structures. (3rd edn), Computers & Structures Inc., Berkeley, USA.
- Liang Z, Lee GC, Dargush GF, Song J (2012) Structural Damping: Applications in Seismic Response Modification. CRC Press, Boca Raton, Florida, USA.
- Lee JJ (2018) The Potential Application of Strain-Induced Stiffening Base Isolation System (Doctoral dissertation), University of California, Berkeley, USA.
- Naeim F, Kelly JM (1999) Design of Seismic Isolated Structures: From Theory to Practice. John Wiley & Sons, Inc., New York, USA, p. 304.






























