Review Article

Empirical Study of Optimal Capital Structure and the Debt Capacity of BOT Projects

Borliang Chen* and Chen-Hung Tang

Department of Civil Engineering, National United University, Taiwan

Submission: February 01, 2019; Published: February 20, 2019

*Corresponding Author:Borliang Chen, Department of Civil Engineering, National United University, Taiwan

How to cite this article:Borliang C, Chen H T. Empirical Study of Optimal Capital Structure and the Debt Capacity of BOT Projects. Civil Eng Res J. 2019; 7(3): 555713. DOI: 10.19080/CERJ.2019.07.555713

Abstract

It is world widely trend for governmental agencies to promote private sectors to participate in the development of infrastructures, such as BOT projects. However, BOT projects are inherently risky due to too many uncertainties during the project period. Overoptimistic in revenue and lack of risk analysis in BOT projects might usually lead the concessionaire to misestimate the project feasibility. This may result in high probability of defaults (PD) of BOT projects and cause financial disaster toward concessionaire. In the worst situation, it could make the projects become unbackable. However, it is rarely to discuss the probability of defaults and bankruptcy cost in the conventional BOT financial model. In general, capital structure of BOT projects is assumed 30% of equity and 70% of debt, and debt repayment is arranged in repaying equivalent uniform annul cost debt in repayment periods. This kind of repayment arrangement does not consider the erratic nature of revenue. It is risky to repay the debt obligation with inflexible repayment term. And, it may lead to high PD of the projects. The objective of this study was to alleviate the risk of project defaults due to the volatility of revenue. A student dormitory project of the national United University in Taiwan is used as an empirical study to demonstrate the analysis. The repayment arrangement proposed in this paper could make the 35% PD of the project reduce to less than 1% PD.

Keywords: BOT projects; Financial measures; Risk analysis; Probability of defaults

Introduction

For mitigating the fiscal burden of government, improving the quality of infrastructure, and increasing the investment opportunities, it becomes world widely trend for governmental agencies to promote private sectors to participate in the development of infrastructure projects, such as BOT projects. However, many BOT projects are long term investments, which are inherently risky. Mostly, the concessionaires of BOT projects are too optimistic in revenue projections and are short of project risk analysis of BOT projects, which both overestimate the project value. Conventional financial evaluation models of BOT projects set the capital structure as D/E=7/3, in common, and repay the debt obligation as the equivalent uniform annual cost. In this financial arrangement, concessionaires are likely to encounter financial difficulty during the project period with shortage of cash flows. For example, the fixed equivalent uniform annual payment for debt may cause great probability of defaults of the project when low revenue or high operating and maintenance cost occur in certain operation periods. Net operating income is the difference between revenue and operating and maintenance cost. And, the project income is considered as the source of project value. Therefore, the net operating income is a critical managerial factor.

The future net operating income is uncertain in every year of operating period, while the debt obligation is uniform annual cost; the probability of defaults is fluctuant. And if high probability of defaults would debase the debt value and make concessionaires find difficulty in financing the projects. In fact, the replacement cost of project facility is a considerable expenditure in operating period. The huge expenditure will outstandingly enlarge the operating and maintenance cost of the years compare to others. If facility replacement took place in the debt repayment periods, the great replacement cost would diminish the ability of repaying the outstanding debt of the concessionaire, and the probability of defaults would increase or even really cause the concessionaire defaults.

If the project company became bankrupt, debt holders would have to pay bankruptcy cost before they could take over the company. Bankruptcy cost will vary the debt value because of the existence of the probability of defaults. The objective of this paper was to evaluate the probability of defaults under different debt repayment arrangement. With the knowledge of the distribution of net operating income, which is defined as a random variable, the probability of defaults, debt and equity value can be calculated. The probability of defaults and promised debt repayment would be determined under three criteria: maximizing project value, debt capacity and value at risk with a confidence level of 99%. The model in this study is named as Probability of Defaults Measures Model (PDMM).

Modeling

The basic theory of the PDMM in this paper is based on the Capital Asset Pricing Model (CAPM) [1-4]. Dais (1995) incorporated the CAPM with capital cost into an evaluation model of project value, in monetary units. A modification of Dais’s formulation for the debt holders’ perspectives is proposed with considering the cost of bankruptcy, the probability of defaults, and the systematic risks. The probability of bankruptcy is the likelihood that a firm’s cash flows will be insufficient to meet its promised debt obligation, either interest or principal.

Bankruptcy cost

Because it is likelihood that the project concessionaire becomes bankrupt and falls into defaults, there is a cost of financing the debt: the bankruptcy cost, . The equation is assumed as follow

Where bf is the fixed cost, bv is the coefficient of X. And, X is the net operating income of BOT project.

Probability of defaults

Suppose that in a specific year of repayment periods of the project, the net operating income was unable to meet the debt obligation. Then the concessionaire would fall into defaults. The probability of defaults is the probability of the state that the net operating income was less than the loan. The net operating income, X, is assumed to be a normal random variable. As the period of debt repayment, Rp, expected value of the net operating income, E[Xi], standard deviation, σX, and the ith year promised debt repayment, di, are given, the probability of defaults, F(di), could be determined. The equation is as follow:

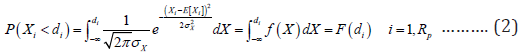
Project value

Frequently, the project value is regarded as one of the most important criteria in the project financial feasibility evaluation. The greater the project value is, the higher the feasibility of the project. But the project would be feasible only if the project value was greater than the project cost. Project value is considered the sum of debt value and equity value, in this study, both debt and equity depend on the net operating income. In a project evaluation, the risk usually reflects in the cost of debt and equity. Base on the foundation theory of CAPM, Dais (1995) derived a model with considering the systemic risk, risk of revenue and the risk of default. The model provides a scheme to evaluate the value of debt and equity individually.

The project value, V , can be calculated by summing the debt, D, and equity, E .

Criteria

Three criteria were adopted in the study:

A. maximizing the project value that generates the optimal capital structure;

B. maximizing the debt value for obtaining the debt capacity; and

C. value at risk with 99% confidence level.

Optimal capital structure

Optimal capital structure (OCS) is the proportion of debt and equity that maximizes the project value. OCS depends on the promised repayment of debt. The value of debt increases when the concessionaire raises the promised debt repayment. On the contrary, the value of equity decreases. As the optimal capital structure was obtained, the probability of default could be determined simultaneously for the given promised repayment.

Debt capacity

Since the net operating income is risky, the expected debt repayment doesn’t continually increase while the promised debt repayment increases. If the promised debt repayment was very near to the net operating income, the expected debt repayment would decrease because of the increasing of the probability of defaults. The present value of the maximum of debt value is the debt capacity, one of the debt holders’ main concerns. Intuitionally, debt holders will not gain their debt when the promised repayment is greater than this critical value.

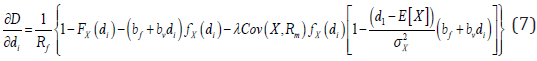
Value at risk-99%

Suppose the debt holders were taking the default risk for the probability of default equals to 1%, the corresponding promised debt repayment would be di in the ith year.

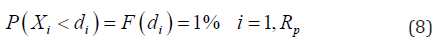
Empirical study

A case of university dormitory of National United University (NUU) in Taiwan is to illustrate the PDMM as an empirical study of this paper. It is a BOT project of dormitory in National United University. The input parameters and results are shown as follow.

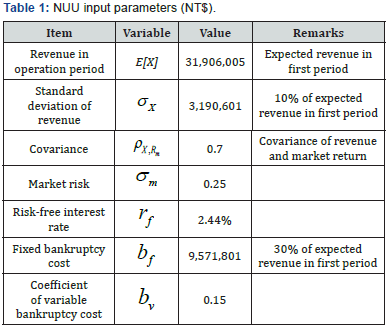
Input parameters

Input parameters of the National United University dormitory BOT project are shown as Table 1. These parameters are useful only when loan relationship exist between the concessionaire and the debt holders.

Results

Figure 1 displays the probability of defaults (PD) under the calculation of conventional repayment arrangement model. Conventional Model(D/E=7/3).

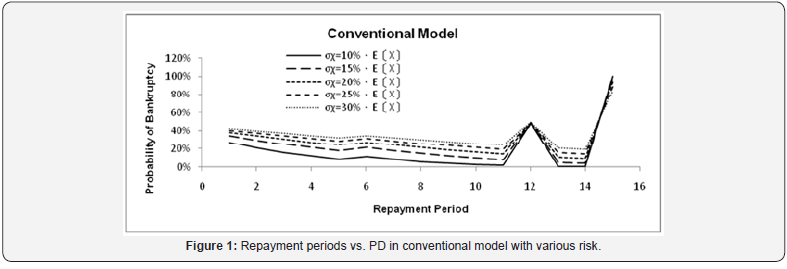
A. Conventional Model(D/E=7/3)

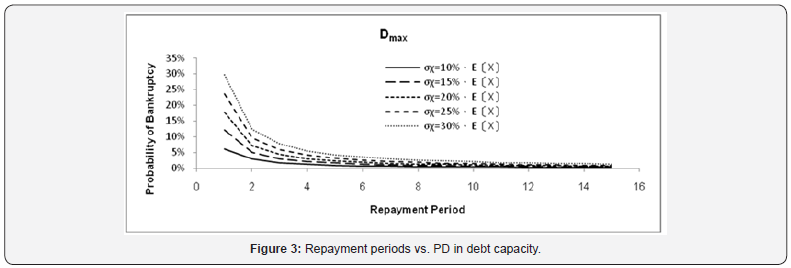
The loan was assumed 70% of total asset in conventional model and the debt principal and interest were repay in equivalent uniform annual cost during 15years of debt repayment periods. The PD is large especially in the 12th and 15th years that the years of replacement expenditure payout. The average PD of σx=20%. E[Xi] is equals to 29.4%. The high PD suggests the difficulty of debt finance. The PDs with two criteria of optimal capital structure and debt capacity in every repayment period of PDMM are shown in Figure 2 and Figure 3, respectively

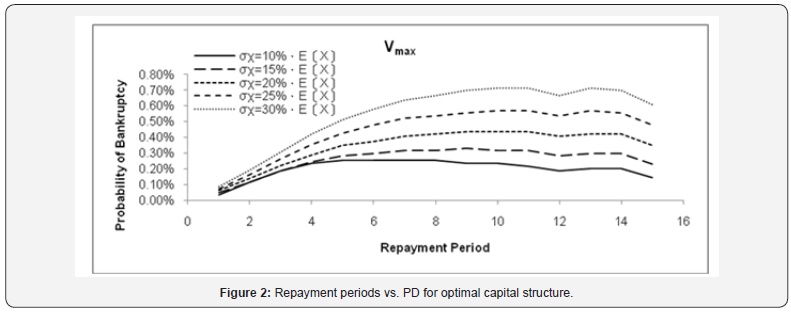
B. Optimal capital structure (Vmax)

Maximizing the project value can benefit to keep PD low, even in case of σx=30%. E[Xi]. The PD remains less than 0.8%.

C. Debt capacity

To evaluate PD with debt capacity, PD are large in the early periods and remain steady in the late periods.

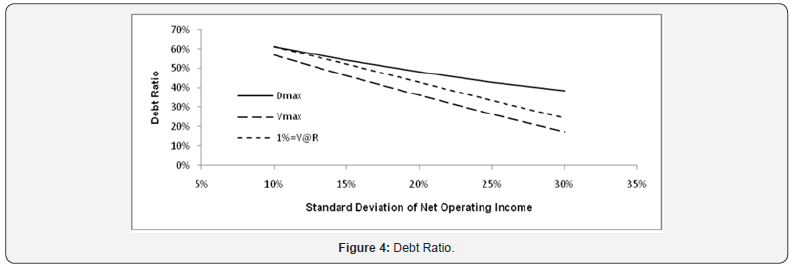
Figure 4 shows the debt ratio (=D/V) with different standard deviation value under the three criteria. The results show less debt finance with PDMM (see Figure 4).

D. Capital structure

Figure 4 illustrate the debt ratio with different standard deviation value under the three criteria. Great value of standard deviation causes less available debt finance. And maximizing the debt value can raise more debt than maximizing the project value. Taking 1% risk of PD can raise more debt than maximizing project value but les than maximizing debt value.

Conclusion

Debt repayment arrangement in conventional model will result in high probability of default. It is very risky for concessionaire to go bankruptcy. Likewise, for debt holders are unable to receive the payback. Therefore, it is suggesting that the debt repayment is necessary to rearrange with considering the characteristic of net operating income every year. Maximizing the project value leads to safer debt finance with low probability of default. However, the disadvantage is that the concessionaire would find it difficult to finance more debt compare to the case of maximizing the debt value. Consequently, making the decision of whether to raise more debt or to improve the project value is essential for concessionaire. No matter which criteria concessionaire select, maximizing the debt value and maximizing the project value, the probability of default reduces dramatically to 1% from original more than 35%. The BOT project becomes very promising and attractive for loan providers.

References

1. Antonio D, Ioannou Photios G (1995) Debt Capacity and Optimal Capital Structure for Privately Financed Infrastructure Project. Journal of Construction Engineering and Management 121(4): 404-414.
2. Wibowo A (2006) CAPM-Based Valuation of Financial Government Supports to Infeasible and Risky Private Infrastructure Projects. Journal of Construction and Management 132(3): 239-248.
3. Kim Han E (1978) A Mean-Variance Theory of Optimal Capital Structure and Corporate Debt Capacity. The Journal of Finance 33(1): 45-63.
4. Chen-Hung T (2009) The Financial Analysis of Government Supports for High Risk or Non-Self-Liquidated BOT Projects. Department of Civil and Disaster Prevention, National United University, Taiwan.