A Pilot Study on Graphics-Based Learning Strategies in Architectural Structures
Bronne C Dytoc*
Department of Architecture, USA
Submission: January 08, 2019; Published: January 24, 2019
*Corresponding Author:Bronne C Dytoc, Kennesaw State University, USA.
How to cite this article:Bronne C Dytoc. A Pilot Study on Graphics-Based Learning Strategies in Architectural Structures. Civil Eng Res J. 2019; 7(1): 555705. DOI: 10.19080/CERJ.2019.07.555705
Abstract
A pilot study conducted to determine whether the instruction of graphic learning strategies for the introductory course on structures in an undergraduate architecture program had a positive effect on students’ learning performance and their attitudes. This paper discusses the pilot study and its results. This topic of graphic learning methods for structures has been developed as a visual-biased alternative to the conventional approach of lecture -drills. Rooted in a few of the emerging trends and theories in instruction, chief of which are multi-media learning theory and embodied learning theory, the approach of employing graphic skills in learning introductory structures continues to develop and improve for motivation, learner engagement, and task performance. The study’s focus encompasses forces, their addition, equilibrium, and the analysis of external and internal forces in trusses. The pilot study, in a quasi-experimental format, assigned one class as the control (lecture, n=35) and another class as the intervention (graphics, n=34). The midterm examination’s main task of truss analysis served as the performance assessment tool. A post-exam survey was also conducted to gauge the attitudes of students of both classes.
Though the naturalistic setting of the classes and low sample population allows for lesser accuracy, the pilot study’s initial findings may already suggest that the use of graphic-based strategies in teaching and learning structures may have a modest positive effect on performance and attitudes. Further research may be conducted to add to these initial findings, as well as address questions of knowledge mastery and transfer into design studio settings.
Keywords: Architecture education; learning of structures; Graphic learning strategies; Multimedia learning; Embodied learning
Introduction of A Teaching Model
In developing an instructional model for the teaching and learning of structures in an undergraduate architecture program, the author proposes that collaboration, embodied action, and explicit practice of graphics skills may serve as strategies to achieve better motivation, engagement, and performance [1]. Certainly, the evident visual bias of architecture design students and particular constructivist aspects of the design studio serve as major influences in the design of the instructional model.
Furthermore, the author proposes that the integration of graphical strategies into its instructional design may serve as a cognitive link between concepts of structure and the mathematical computations that are normally utilized. The teaching and learning model offered by the author is one that employs collaborative teams with a scaffolded learning structure. In integrating the practice of graphic skills in the instruction, these drawing practices would visually help students learn the logic of force systems more confidently, while also associating these cues cognitively in generating the equations used for numerical analysis.
Review of the Main Considerations in the Re-Designing of Instruction
Multimedia: text and graphics
In addressing the issues of appeal and engagement in math and science instruction, use of well-designed visuals with narratives aids with problems of cognitive load, particularly for visual learners [2,3]; in short, the right kind of graphics delivered appropriately with instruction is more effective than without them [4]. Many of these graphically-aided approaches to teaching are based on the multimedia learning theory by Mayer [5]. In his work, Mayer discusses how text (hearing) combines with graphics (seeing) to access prior knowledge, and, hence, construct new knowledge. For a structures course, it would follow that the use of graphics in instruction can guide students better in learning structural logic and writing the force -equilibrium equations from the drawings’ cues. The nature of drawings and diagrams would also help to give the class a more familiar architectural flavor (Figure 1).

Scaffolded and collaborative learning
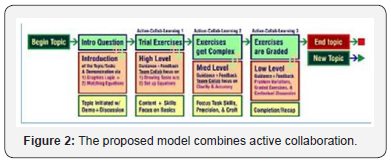
While most of the topics in introductory structures are not complicated, these many sets of steps build upon other sets of steps, making the learning of tasks quite complex, particularly for novice learners; scaffolded modes of instruction are recommended to optimize complex learning while managing cognitive load [6] (Figure 2). Furthermore, knowledge can strengthen in the class’ social environment when peers activate collaborative learning [7] with clarifying arguments and discussion [8] (Figure 3). These collaborative learning “territories” swing the class environment to the students’ favor, allowing for more channels of communication between instructors, learners, and their peers. Interactive participation trumps passive reception of content [9,10].

Learning by actual drawing action
“Learning by doing” is an old and enduring phrase. Surely there is something to it; Mueller and Oppenheimer state that learning is better when notes were written by hand, instead of taken with a laptop [11]. The key idea is the engagement of the mind in interpreting knowledge into self-authored notes, instead of just taking copious notes without the comprehension of content. Similarly, in early design studio, exercises develop skills and craft through manual execution. Thus, seizing on the learners’ unique capacity to draw precisely, and using these very motions to aid in the learning of often-elusive structural concepts, the instructional model takes graphics a step further by incorporating embodied learning (learning with/through intentional motions) [12]. Just like dance or sports, mastery of knowledge would translate to learning with intentional movements and muscle-memory [13].
Why Redesign the instructional model?
Considered for the achievement and cultivation of mindful learning [14], the proposed model for teaching and learning expands on the conventional cognitivist approach to learning math and science; it involves activated graphics, scaffolded collaboration, and embodied learning methods. Associations developed with these multimodal strategies aim to effect better mastery and engagement [15]. But really, why bother? Won’t this just be making a challenging class more confusing? Regarding teaching and learning, there are pros and cons to doing either method. With the math -only approach, the familiarity offers the student a feeling of less stress, with learning happening only in one mode. However, as the author has repeatedly observed, this mathematical form is not the architecture student’s regular mode of expression. Thus, the learner’s mind is more loaded as it comprehends a multiple-force exercise and translates it directly into its equational forms. And with this approach, the student must stay on top of several things: Are all the forces accounted for? Are their components derived accurately? Are their orientations properly signified (+/-)? What does a positive or negative final answer mean?
With the incorporation of precise graphics, all forces are accounted for more easily as they are drawn to scale. Each force’s arrowhead orientation, and its projection into X and Y components states whether it sign would be a “plus” or a “minus”. Using these visual cues directly into equations will show that correct final answers will always be “positive”. Compared to the conventional approach of computations, this integration of drawing does pose an additional load; however, doing graphics correctly unloads their head of doubts and firms up their competency in the end task of solving equations. Along with this competency comes the motivational boosts of satisfaction and confidence [16]. So, the question now is: does it work?
The Design of the Pilot Study
A quasi-experimental Setup
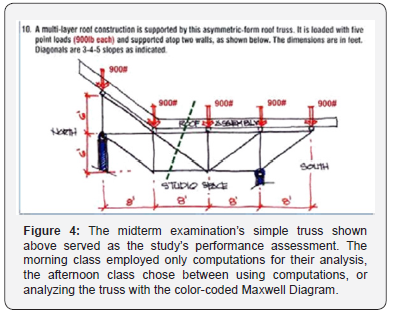
Similar to an experiment, the pilot study’s hypothesis asks whether the integration of graphical skills makes for better learning versus the conventional cognitive format of calculations alone. There were only two sections for this study; the morning control group (n=35), and the afternoon intervention group (n=34). Active-collaborative instruction was practiced in both sections. However, the morning class focused solely on the mode of analytical equations as its operating “dialect”, while the afternoon class practiced the two modes of precise drawing and the writing of equations for analysis. The topics of forces, equilibrium, and moments built upon each other towards the major task of analyzing simple trusses completely. Figure 4 shows a sample of the main exercise of truss analysis given in the midterm examination; this challenge served as the study’s measurable assessment.
Measures of performance and engagement
Although novice learning is facilitated with the use of active collaboration, the end goal of the instruction is achieving individual knowledge mastery. Hence, using the midterm test’s major exercise as a performance assessment device was logical. It allows for individual performance to be measured in a controlled and timed environment. Performance was measured in terms of completeness and correctness of the required analysis. As a correlational measure, completion of the midterm test itself against time was also noted. Finally, for a window into student attitudes, an informal survey was given one week after the midterm test was conducted.
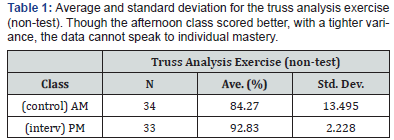
Before a report on the raw findings of the midterm test begins, a quick explanation must be given as to why this pilot study did not include regular non -test exercises (aka in-class works, or home works were not considered). Of the different valid reasons, the main one was the possibility of peer collaboration presence in the individual exercises. As groups form a bond during collaboration, this mechanism often pervades into the graded work; and while this may be part and parcel of a more effective learning experience at the scale of the class itself, it does not represent a measure of individual competency (Table 1).
The Test and the Observed Results
The main task: truss analysis
The assessment measures the knowledge and skills in the addition and equilibrium of multiple forces, moments, and their application into the analysis of a truss for its external reactions and internal bar forces. Shown below are comparative solutions to the analysis of the truss. Figure 5 shows the conventional application of equations of equilibrium, and the alternate approach of balancing with fractions, to determine external reactions to the assigned loads. A moment equation selects a reference point as a pivot, and all forces are paired with corresponding distances (measured from the pivot point). Fraction-ratios employ the understanding of uneven seesaws or balances to generate reactions for each force or force group.
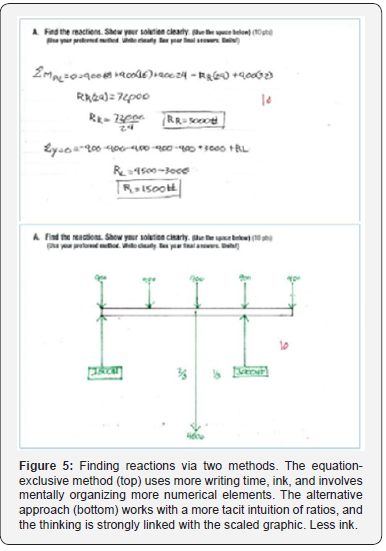
Conventionally, the dominant code of analysis is calculations; in the author’s opinion, this has the tendency of relocating the student’s mind away from the presented graphics to another “place”. Alternatively, the author believes that practicing fractions or ratios integrates graphic intuition in applying principles of moments. Both approaches are technically valid as both solving strategies are based on the same concept of moments or torque. However, less ink (and thus less time, and perhaps, less mental clutter) is involved in the practice of fractioning loads into their reaction locations. Once external equilibrium is established, the work proceeds to finding internal forces. Figure 6 shows two approaches: the conventional method of joints with its usage of Σ X/ΣY equilibrium equations, and the alternative method of graphically drawing nested force loops onto one another in proper scale, aka the Maxwell Diagram. As seen in Figure 6, computations dominate in the conventional method of joints. Maybe familiar to students, this mode of mathematical communication is not always practiced masterfully by students. The writing and processing of equations carry with them corresponding rules of logic and syntax that need to be observed. For the structural topics in particular, the use of positive or minus signs in an equation need care in their setup to avoid misdirection. Once equations are fully processed, a positive or negative sign in the resulting answer does not signify direction but confirmation, thus lending another meaning to the same symbols. Furthermore, the directional orientation of the forces, even when correctly done, does not directly signal that a force has a compressive or tensile nature; another act of decoding is necessary. Finally, and often overlooked, the directions of forces at a joint must be reversed at the next adjacent joint to be analyzed, whether positive or negative. Otherwise, misdirection will compound embedded errors in further joints to be analyzed. That is certainly a lot of important details to keep track of in the head of an architecture student who does not regularly practice the language of math and algebra as familiar territory.
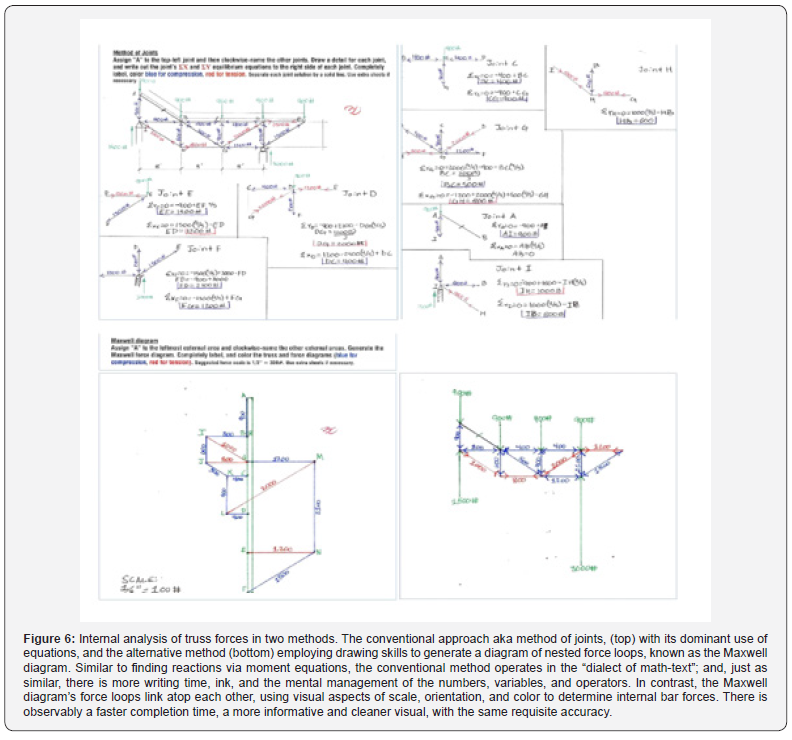
In the alternative method of drawing force-loops, there are also corresponding rules of operation to follow. In analyzing a truss joint, known forces must be sequentially drawn as a chain of scaled vectors, with their arrowheads forming a oneway traffic run. This clues in a goal of continuing the run with the orientation of the two unknown truss bar forces, handily establishing equilibrium when the run returns to the starting point. In applying this method, the guiding rule of one- way traffic chain of vectors reveals force directions visually. The arrowheads transferred to their respective bars in the joint detail also reveal the compressive or tensile nature of the force. Then comes the simple step in the procedure to “mirror-image” (reverse) each force’s arrowhead direction at the other end of the bars. Setting up equilibrium equations becomes a straightforward, direct translation the graphic drawing’s arrowhead directions into the corresponding positive or minus signs, sans guesswork.
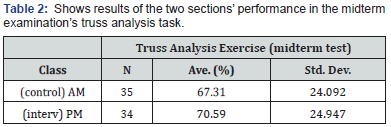
What is Suggested by the Performance Numbers?
Table 2 shows results of the two sections’ performance in the midterm examination’s truss analysis task. On initial review, the average performances from both classes show no significant difference. Furthermore, both classes display the same large variance in scores (std. dev.). The initial reaction would be to say that the graphical techniques in the pedagogy were not working better as an alternative. However, on review, the researcher then recalled that students in the intervention class were allowed to select their preferred method in analyzing for truss forces. Table 3 below shows a clarified view of the results from the intervention class alone; scores show a marked difference between those that practiced the conventional method vs. those that utilized the graphical approach.
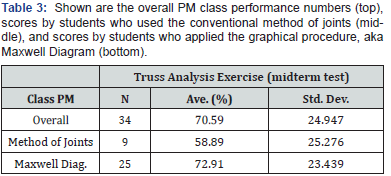
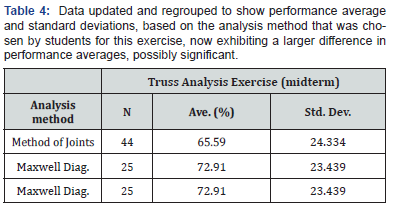
With this clarification, the numbers were re-grouped to respond better to the study’s research question, “Will the integration of graphics in the instruction improve learning performance in this particular set of structural topics?” Table 4 shows the performance numbers updated to reflect scores based on the chosen analysis method utilized for the exercise, instead of class time. What the numbers now suggest is that the integration of graphical skills in the instruction may have a positive effect on the learning.
A Supportive Clue: Pace of Completion
In both the control and intervention classes, I began the test session by settling the students into their seats, giving the students their test packets, reminding them of testing procedures, and wishing them good luck. The midterm test, as a whole, was designed for a time period of 2.5 hours. At the 2 -hour mark, I noted how many have submitted their exam. Reminders of time were announced at 10 minutes, 5 minutes, and 2 minutes to the ending time mark of 2.5 hours. At this point, those who were still working on their test had to submit them in. I then took note of how many were “unfinished” at this time. The table below lists the differences between the AM and PM classes, in terms of their relative performance completion.

As Table 5 shows, the AM control class was relatively slower, with fewer students done at 2 hours, and four students unfinished by the final submission time mark of 2.50 hours. The PM class had more students done at both time marks. Notably, the one person in the PM class who was not able to complete the test happened to start the examination an hour late. This observation may serve as a correlational clue or it may mean nothing. However, let me offer the proposal that this measure of relatively better testing speed may point to a higher level of knowledge competency under pressure in the intervention PM class, and this competency may be an influence on students’ self-confidence. This may find further support in the fact that intervention-class students who scored the worst on this midterm’s truss analysis task opted to apply the conventional method of analysis; somewhat expectedly, they were observably less confident, and took their test to the end of the time limit.
Survey Results-Student Feedback
One week after conducting the midterm examination, an online survey was administered to try to gauge student attitudes towards the class and the teaching-learning approaches. Questions were asked for their feedback on different aspects of their experience: overall satisfaction, content organization, instructional clarity, class pacing, collaborative learning effectiveness, works done in-class, and their attitude towards their chosen analysis method. For many of these questions regarding their learning experience, the survey data were similar from both the control and the intervention class. Satisfaction overall was at 66 -68%. 70-80% felt the classes were well organized. 43-45% felt the classes were paced just right. With the extra load of learning graphic skills, the afternoon class, expectedly, had a higher percentage of students who felt the pace was slightly fast. Both classes felt that the clarity of instruction was similarly mixed. 68-82% felt collaborative learning was effective. 80-82% approved of doing exercise works in class. Students also submitted candid commentary. The overall picture from their statements strongly suggested for an atmosphere of collaboration in the learning, a steady diet of in-class works, a resonance with scaffolding techniques to build up their mastery of knowledge and skills, and an avoidance of being “thrown into the pool” with discovery learning techniques [17,18]. Of the different questions asked in the survey, I realized I could not ask the most relevant question: whether the conventional analysis method of joints or the graphics-integrated method of force-loops was the more preferred approach to learning truss analysis.
Unsurprisingly, the majority of students in the afternoon class opted for the graphic Maxwell diagram method vs. the equational method of joints. Their better task performance and their faster completion pace would have contributed to a stronger sense of satisfaction and confidence. Most importantly, they were able to answer this question because they were equipped to analyze a truss both ways and had a choice as to which method they preferred. But I could not ask a similar question of the morning control class; they were given only the conventional approach that used conventional math procedures. With no exposure nor experience in the alternative approach, these students could not qualify to respond informatively to this key question. Therefore, I had to ponder on that point, as well as think on the initial findings of this pilot study.
Reflections and Recommendations
In thinking of what this initial study’s findings may mean, and how the control-intervention testing setup may improve for future research, I realize I could also temper my expectations. I should remind myself that the pilot study is not strictly an experiment; this is due to many naturalistic factors or conditions that could not be strictly regulated. Students were not randomly assigned to the morning or afternoon class; the level of alertness and energy in students themselves may have been different from one time of day to another. The quality of daylight across the hours could also affect the perceived ambiance of the physical learning environment, etc. Factors that vary due to the difference of time could contribute to differences, yet the causes may not be easy to pinpoint. Thus, while the study is designed and conducted to be as close to an experiment as possible, it really is quasi-experimental, and conclusions could not be reported as reliably absolute; they can only be, at best, strongly suggested or inferred; this is a point made more evident with the study’s lowpower population of n~70.
Nevertheless, even if the statistical power of the study can only be mild or fair at best, particular points regarding the improvement of instruction can already find some backing. While the research shall continue to develop along the direction of graphics integration in the instruction, the author recognizes that the strategy, selected to align with the architecture students’ visual learning bias, can also be considered an application of Mayer’s multimedia learning theory, or a deliberate strategy of weaving different yet associated media modes in teaching [19]. I hope to be able to investigate this topic of instruction as a longitudinal study, with incremental updates.
References
- Dytoc B (2017) Activating Graphics and Collaboration in Architectural Structures Education. The New ARCH International Journal of Contemporary Architecture 4(2): 15-26.
- Strauss, Judy, Corrigan, Hope Hofacker Charles F (2011) Optimizing Student Learning: Examining the Use of Presentation Slides. Marketing Education Review 21(2): 151-162.
- Lin L, Atkinson RK (2011) Using animations and visual cueing to support learning of scientific concepts and processes. Computers & Education 56(3): 650-658
- Diezmann C, Lowrie T, Sugars L, Logan T (2009) Students’ Sensemaking with Graphics. Australian Primary Mathematics Classroom 14(1): 16- 20.
- Mayer RE (2009) Multimedia Learning. Cambridge Cambridge University Press.
- Merriënboer J, Kirschner P, Kester L (2003) Taking the Load Off a Learner’s Mind: Instructional Design for Complex Learning. Educational Psychologist 38(1): 5-13.
- Nicol D, Boyle J (2003) Peer Instruction versus Class-wide Discussion in Large Classes: A Comparison of Two Interaction Methods in the Wired Classroom. Studies in Higher Education 28(4): 457-473.
- Vo HX, Morris RL (2006) Debate as a tool in teaching economics: Rationale, technique, and some evidence. Journal of Education for Business 8: 315-320.
- Hake RR (1998) Interactive-engagement vs traditional methods: sixthousand- student survey of mechanics test data for introductory physics courses. American Journal of Physics (1): 64-90.
- Hoellwarth C, Moelter MJ (2011) The implications of a robust curriculum in introductory mechanics. American Journal of Physics 79(5): 540-545.
- Mueller P, Oppenheimer D (2014) The Pen is Mightier than the Keyboard: Advantages of Longhand over Laptop Note Taking. Psychological Science 25(6): 1159-1168.
- Merriam SB, Caffarella RS, Baumgartner L (2007) Embodied, Spiritual, and Narrative Learning. Learning in Adulthoo: a comprehensive guide.
- Katz M (2013) Moving Ideas: Multimodality and Embodied Learning in Communities and Schools. New York Peter Lang Publishing 71(3): 307-308.
- Langer E (1997) The Power of Mindful Learning. Boston MA Addison- Wesley.
- Dirksen J (2012) Design for How People Learn. Berkeley, CA: New Riders. Berkeley California, USA, pp. 1-64.
- Keller JM, Deimann M (2012) Motivation, volition, and performance. In: Reiser RA & Dempsey JV (Eds.), Trends and issues in instructional design and technology, Boston, MA: Pearson, USA, p. 84-95.
- Kirschner PA, Sweller J, Clark RE (2006) Why Minimal Guidance During Instruction Does Not Work: An Analysis of the Failure of Constructivist, Discovery, Problem-Based, Experiential, and Inquiry-Based Teaching. Educational Psychologist 41(2): 75-86.
- Mayer RE (2004) Should There Be a Three-Strikes Rule Against Pure Discovery Learning? American Psychologist 59(1): 14-19.
- Mark G, Hans Van Der M, Ton De J, Jules P (2002) Multimodal versus Unimodal Instruction in a Complex Learning Context. The Journal of Experimental Education 70(1): 215-239.






























