Comparative Analysis of the Use of the Pore Pressure and Humidity When Assessing the Influence of Soils in Transport Construction
Kochetkov AV*
Perm national research Polytechnic University, Russia
Submission: November 20, 2018; Published: December 13, 2018
*Corresponding Author:Kochetkov AV, Perm national research Polytechnic University, Russia.
How to cite this article:Kochetkov A. Comparative Analysis of the Use of the Pore Pressure and Humidity When Assessing the Influence of Soils in Transport Construction. Civil Eng Res J. 2018; 7(1): 555704. DOI: 10.19080/CERJ.2018.07.555704
Short Communication
Now there is a question of reasonable applicability of indicators of pore pressure and humidity at an assessment of influence of indicators of soil in various environments and conditions of transport construction. Such an analysis can be carried out within the framework of the molecular kinetic theory of gases taking into account the photon interaction.
The real gas is not described by the clayperon-Mendeleev equation for ideal gases. Therefore, due to the needs of practice, many attempts have been made to create an equation of the state of real gases.
The most well-known equations for real gases are given in Table 1.
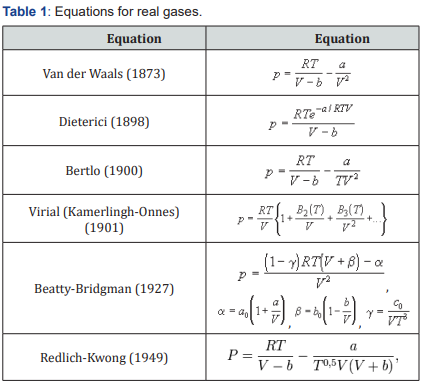
Some equations are a refinement of the equation of van der Waals (Dieterici and Berta), and equation Beattie-Bridgeman and Redlich-Kwong are empirical, without physical justification. In this case, Redlich writes in his article that the equation does not have a theoretical justification, but is, in fact, a successful empirical modification of the previously known equations [1]. A large number of equations due to the fact that no equation describes the behavior of real gases under all possible conditions (temperatures and pressures). Each equation has areas in which it best describes the state of the gas. But in other conditions, the same equation has large deviations from the experimental data. In practice, only the van der Waals equation is used in the form of direct calculations due to its simplicity. For other equations, either charts or tables of calculated values are typically used.
The meaning of the van der Waals equation is not only that it is the simplest, but it also has a clear and simple physical meaning. “Despite the fact that the equation of van der Waals equation is an approximate, it is sufficiently well suited to the properties of real substances, so basic provisions of the theory of van der Waals forces remain in force to the present time, exposed to the modern theories that only certain clarifications and additions” [2, p. 59]. “It was indicated that the modern theory of the equation of state of real gases is based on the fundamental provisions of the theory of van der Waals and develop these provisions further, and, having powerful mathematical apparatus of statistical mechanics, it gets the ability to produce all calculations are approximate, but quite accurate” [2, p. 60].
The citation clearly indicates that statistical mechanics is used for accurate calculations based on physical models.
The fact is that thermodynamics is a phenomenological science. It is possible to obtain experimental data on the state of gases at different thermodynamic parameters and to approximate the most suitable thermodynamic equation even without having any idea of the internal mechanisms of the processes occurring in the gases. This is exactly what the authors of the gas laws did: Lavoisier, Boyle, MARRIOTT, etc.
But if you try to delve into the essence of the processes occurring in gases, then a mathematical apparatus is inevitably necessary, taking into account the interaction of the molecules and atoms that make up the gases. This is the apparatus of statistical physics. But, to statistical physics problems of their own. “The exact theoretical calculation of the statistical sum of gases or liquids with arbitrary Hamiltonian (2.6) is a problem that lies far beyond the capabilities of modern statistical physics” [2]. Although,” it is possible to make a number of reasonable and sufficiently good approximations that allow us to estimate the statistical sum (2.1) and the configuration integral (2.8) for real gases consisting of valence saturated molecules “ [2]. The task is still far from over. A reasonable choice of initial parameters plays an important role in the difficulties faced by researchers of real gases. We will carry out a methodical analysis of the initial parameters used in the theory of gases. Currently, the following thermodynamic parameters are used in the scientific and educational literature: P (pressure), V (volume) and T (temperature). If the temperature and volume are not in doubt, the pressure, as a thermodynamic parameter, raises certain questions. Consider the compressibility factor (a measure of pressure of gases). It is believed that “the most convenient measure of nonideality is the compressibility factor Z = pVm / RT, since for an ideal gas Z = l under any conditions” [2]. For example, it is proposed: “the thermal equation of state of a real gas can be represented in the form pv = zRT,
where z is the compressibility factor, which is a complex function of temperature and density (or pressure)” [3].
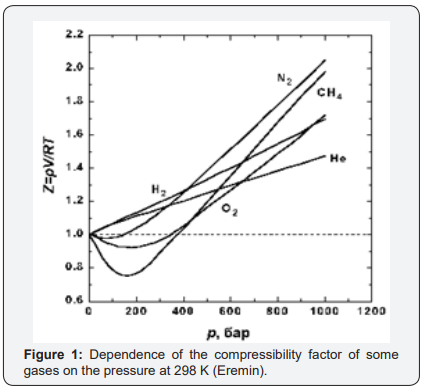
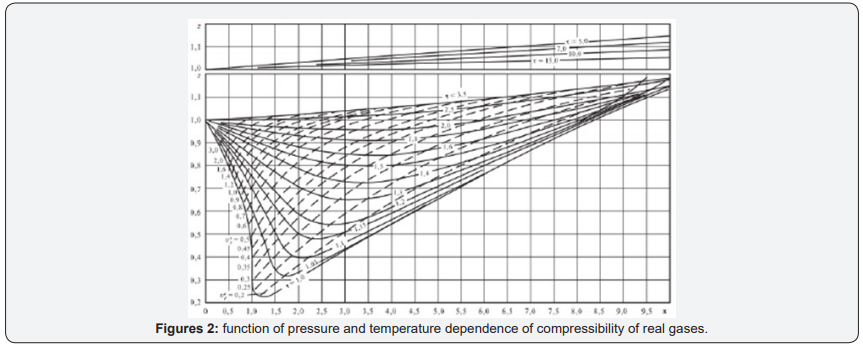
But as a parameter for determining the thermodynamic state of the gas system, compressibility is not very suitable, because firstly, it has a complex dependence on pressure and temperature. Any explanation of why and what determines the compressibility of gases is determined by the adopted model of the structure of gases. The form of the compressibility function for all real gases is given in [3] (Figure 1), and “for generality, the reduced pressure π=p/PK and the reduced temperature τ=T/TC are used as parameters here, where PK and TK are the parameters of the substance at the critical point. Since for an ideal gas at any parameters z=1, this graph clearly represents the difference between the specific volume (density) of the real and ideal gases at the same parameters”[3] Figure 2.
Secondly, the compressibility of gases cannot be directly measured during the working cycle of a thermodynamic system, but only during specially conducted experiments. Third, the compressibility of gases, in fact, is not a single curve, but a family of curves, at different temperatures and the same pressure, or at the same temperature, but different pressures, the compressibility of the gas is different. In practical work, the compressibility of gases is not measured, but calculated according to the appropriate calculation formulas, according to officially recognized methods. Therefore, the compressibility of gases may well characterize the nonideality of gases but cannot be accepted as an initial parameter in the theory of real gases. Let’s see what else can serve as a replacement for the pressure as the initial parameter. For this it is necessary to pay attention to the parameters that are used in the statistical theory of gases. The literature analysis shows that all statistical models of real gases are constructed using such parameter as concentration. Concentration is the number of atoms (molecules) per unit volume.
This is not surprising, since it is the concentration that determines the average distances between the gas molecules, and hence the potential long-range forces of the molecules. For example, according to the theory of van der Waals or any other. Then, after establishing the laws of behavior of the statistical system depending on the concentration, go to the usual thermodynamic characteristics: P, V, Etc. The application of pressure as a thermodynamic parameter is perfectly justified in the theory of ideal gases, in which atoms interact only at absolutely elastic collisions during chaotic thermal motion. According to the theory of ideal gases, the relationship between pressure and gas density is very simple [4]:
P = NkT ……………… (1)
here P-pressure, MPa; N-concentration (1/m3); T – temperature.
At a constant temperature, the dependence between concentration and pressure is linear:
P = const*N …………….. (2)
The concentration of N is equal to the number of molecules per unit volume. Concentration is related to density by a simple ratio:
ρ = N*m …………………. (3)
where ρ is the density, N is the concentration, m is the mass of the molecule.
In other words, in the theory of ideal gases, the gas pressure is linearly proportional to the gas density. For real gases this is never the case. The theory of real gases takes into account the forces of interaction of a potential nature. “Real gases differ from their model - ideal gases - in that their molecules are finite in size and between them the forces of attraction (at considerable distances between molecules) and repulsion (when molecules approach each other)” [5]. This leads to the fact that the density of real gases will be nonlinear, and a simple replacement of the concentration of the pressure in the volume, as is quietly done in the theory of ideal gases cannot do.
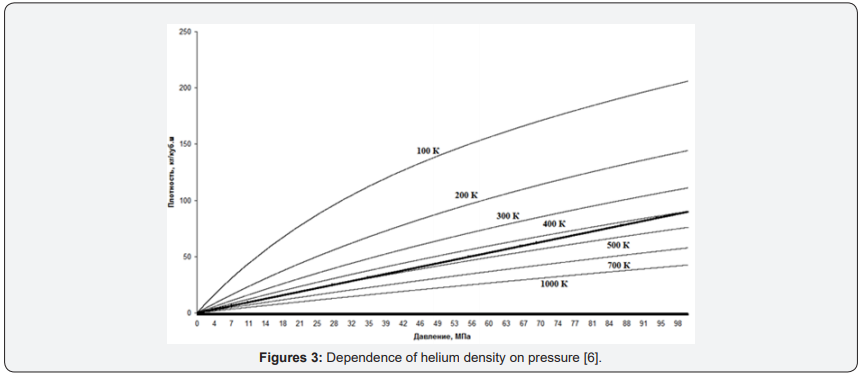
Tradition of determining the parameters of gas pressure is since when in science was not known that gases consist of atoms [5, p. 36-65], and therefore, scientists could not operate with concepts of the concentration of atoms in gases. We do not consider it advisable to continue this vicious practice. Moreover, as mentioned above in the theory of real gases directly refers to the value of concentration, but in the final equations go to the pressure, “the old-fashioned way.”
For Figure 3 graphs of helium density change depending on pressure are given. The fat line is a theoretical line based on the ideal gas model [6].
From Figure 3 it is clearly seen that for the graph of the function for helium, not only does not coincide with the theoretical, but the dependence of the density on the pressure is not linear. We chose helium, not only because the characteristics of this gas are well studied, but primarily because helium is the most chemically inert gas. Due to its inertness, it is not located to form compounds in molecules and other aggregations. That is, in its chemical properties, it is closest to the ideal gas. We chose helium, not only because the characteristics of this gas are well studied, but primarily because helium is the most chemically inert gas. Due to its inertness, it is not located to form compounds in molecules and other aggregations. That is, in its chemical properties, it is closest to the ideal gas. When discussing compressibility as an initial parameter, we said that the main disadvantage of compressibility as a parameter is not direct measurements, but calculated values. Unlike compressibility, the density of gases can be measured directly, both in stationary gases (in tanks) and in pipelines. There are several types of density meters for both liquids and gases. Although densitometers are more expensive than manometers, but the gain in practical applications can be tangible.
Thus, based on modern theories of real gases, it seems more logical to determine the properties of gases, depending not on pressure, but on density.
1. First, because all models of statistical physics are based on the concept of concentration, not on the concept of pressure.
2. Secondly, because it is the density that is closest to the concept of concentration. And easily translated into one another.
3. Third, even if any characteristic of the gas (heat capacity, thermal conductivity, etc.) linearly depends on the density, in accordance with the models of the statistical theory of gases, the translation of the values of these properties depending on the pressure will make an additional nonlinearity, depending on the density of the pressure. Especially if the dependence of the function is nonlinear
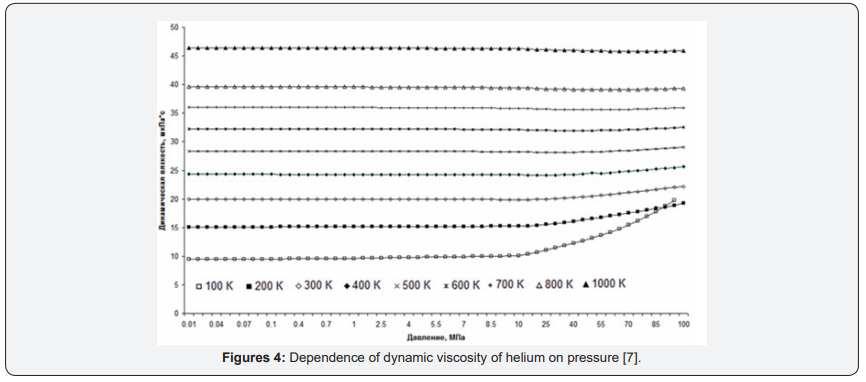
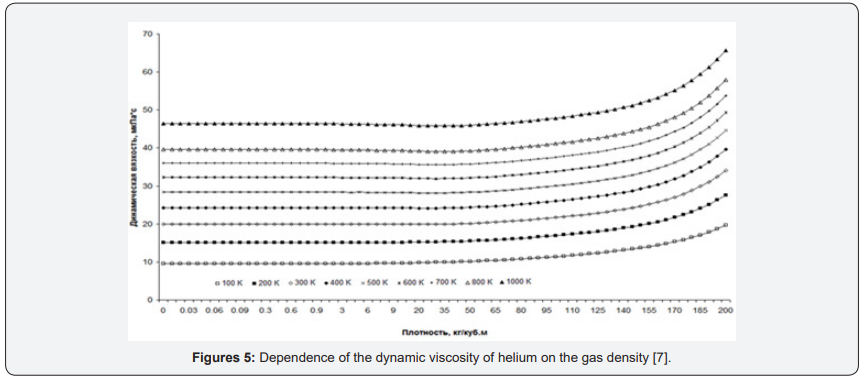
As an example, consider the graphs of the dynamic viscosity of helium. For Figure 4 graphs of helium heat capacity versus pressure in the temperature range from 100K to 1000K are presented. For comparison, graphs of dynamic viscosity versus gas density are presented [7] (Figure 5).
The difference in the representations of the same gas property depending on different parameters is clearly seen from the graphs. The first thing we can say is that schedules of dependence of dynamic viscosity to the density look easier than the dependence of dynamic viscosity on the pressure is because of the nonlinearity of the dependence of concentration on pressure. In particular, viscosity graphs from pressure change their direction of change. And at low temperatures so quickly that the lines even intersect. Moreover, if at low temperatures (lower lines in Figure 3), under high pressure upwards, at moderate temperatures, horizontal, and at high temperatures (top line) a bit, about 2% down.
The graphs also depend on the density - all the lines are almost parallel throughout. And they do not change their behavior at all. But the fact that the graphs depending on the density (concentration) look easier is not the most important thing. The main thing is the epistemological value of such a transition to another parameter [5].
Summary
1. Another proof of the influence of thermal photons on the behavior of gases under different conditions is the experimental data on the compressibility of gases under different conditions.
2. Modern theories of real gases are unable to explain the behavior of the compressibility function. Nothing to do with the change in the density, and especially at different temperatures. Because according to modern theories repulsion of molecules should be observed only when molecules are smaller than the size of molecules. And the compressibility of gases should not depend on temperature at all.
3. The hypothesis of a significant influence of thermal photons on the mechanical properties of gases can explain the behavior of the compressibility factor of gases.
4. With an increase in the density of the gas, the compressibility factor increases because, together with an increase in the density of gases, the number of photons having a mechanical effect on the gas molecules also increases.
5. As the temperature increases, the energy of thermal photons increases, so does the compressibility factor (resistance of the gas to compression). Because more energetic photons have a stronger mechanical effect (stronger push) on the gas molecules. That is why the compressibility factor increases in the temperature range from 10 to 150 K.
6. At temperatures of more than 150 K, the number of thermal photons that have a mechanical effect on the gas molecules decreases, since the radiation of the gas outside increases. Increasing the number of photons leaving the volume of gas.
7. Reducing the number of photons in the gas volume reduces the internal pressure of the gas and, accordingly, the compressibility factor decreases.
8. The moisture index (corresponding to the concentration or density) used in the measurement of soil properties more accurately and reliably (has a large proportion of the explained dispersion) shows a more significant change in its properties in comparison with the pore pressure.
9. Accordingly, there is no reason to move to foreign standards based on pressure indicators in soils and other environments of transport construction.
References
- Vukalovich MP, Novikov II (1948) Equations of state of real gases. Equations for real gases. ML: State Energy publishing house, Washington DC, USA, p. 340.
- Eremin VV, Kargov SI, Kuzmenko NE, (1988) Real gases Chapter 1. Electronic textbook. Physical chemistry Department of Moscow state University, Moscow, Russia.
- Aleksandrov AA (2004) Thermodynamic basis of the cycles of thermal power plants.
- Levich VG, Vdovin Y, Myamlin VA (1971) Course of theoretical physics. Volume 2 Quantum mechanics, quantum statistics and physical kinetics, Moscow: Science, Russia, p. 936.
- Cohen IM (2018) Engineering thermodynamics. Part 1. Electronic textbook, Department of TOT, Washington DC, USA.
- Sychev VV, Vasserman AA, Kozlov AD, Spiridonov GA, Zimanyi VA (1984) Thermodynamic properties of helium. Moscow: publishing house of standards, Russia, pp. 320.
- Alexandrov AA, Orlov KA, Ochkova VF (2018) Properties and processes of atomic energy materials and working bodies.
- Kochetkov AV, Fedotov PV (2015) On the dogmas of faith in the natural and exact Sciences//New science: the current state and ways of development. Sterlitamak: RITZ AMI, Russia, p. 240.






























