System Analysis and Optimization of Multi-Contaminant Water Reuse Network with and without Regeneration using a Hybrid Genetic Algorithm
Sule Abdullahi1*, Ruth Falconer2 and Joseph Akunna1
1School of Science, Engineering & Technology, Division of Natural & Built Environment, Abertay University, Dundee, UK
2School of Arts, Media & Computer Games, Division of Division of Computing and Mathematics, Abertay University, Dundee, UK
Submission: December 04, 2017; Published: March 19, 2018
*Corresponding author: Sule Abdullahi, School of Science, Engineering & Technology, Division of Natural & Built Environment, Abertay University, Dundee, UK. Tel: ab
How to cite this article: Sule A, Ruth F, Joseph A. System Analysis and Optimization of Multi-Contaminant Water Reuse Network with and without Regeneration using a Hybrid Genetic Algorithm. Civil Eng Res J. 2018; 4(1): 555628.DOI: 10.19080/CERJ.2018.04.555628
Abstract
This paper proposed methodology to analyse the possibility of combination of hybrid optimization function with Single-Objective genetic algorithm (SOGA) for solving the multi-contaminant water reuse network with and without regeneration design problem. A non-linear model was considered due to non-linear multicontaminant constraints system. The freshwater use and wastewater production has been minimized, by applying the proposed method. Moreover, the parameters related to the implementation of the genetic algorithm that increase computer speed and satisfy optimum result were tuned before the result is confirmed. The solutions and parametric values so obtained have been further compared with the existing literature values. The results obtained are in agreement and comparable to those obtained from other methodologies and it even shows better result in considering multi-contaminant water reuse with regeneration.
Keywords: Optimization; Genetic algorithm; UNESCO; Heat-integrated water; Computational strategies
Abbreviations: SOGA: Single-Objective Genetic Algorithm; WNS: Water Network Synthesis; WNA: Water Network Analysis; WAP: Water Allocation Planning; WAN: Water Allocation Networks; OTWA: Optimal Total Water Network; GA: Genetic Algorithm; IWN: Industrial Water Networks
Introduction
Water is a key element for the normal functioning of many industries. It is intensively utilised in food, pulp or paper, pharmaceutical, petrochemical and chemical industries, and so on. The industrial revolution inspired many industrial processes that utilize water and dispose of it with a certain concentration of pollutant. The waste water generated from industrial processes is usually treated in a central common facility in order to remove contaminants and to meet regulatory specifications for wastewater disposal.
However, as opposed to this conventional approach, reusing and re-routing the water streams in an integral water network helps in reducing the consumption of freshwater in the system, and minimizes the amount of wastewater to be treated and disposed of in to the environment. Reusing and re-routing the water streams can account for significant financial investment in a plant (industry), as the cost of the treatment units is dependent on the volume of wastewater that requires treatment. Furthermore, in certain instances the level of treatment required is quite substantial. Hence, it would be favourable if the volume of water that requires treatment were reduced.
This leads to research in water-reuse, recycling, and regeneration-reuse/recycle as a means of minimising freshwater use and wastewater production. Regeneration involves partial treatment by using water treatment and purification technologies such as membrane and steam stripping prior to reuse or recycle. These different options for minimising the volume of water used by the industries combined together are termed water network synthesis (WNS) or water network analysis (WNA) or water allocation planning (WAP).
Some of the works done in the area of water minimization in continuous and batch processes are described by the detailed reviews of [1], Foo, Khor et al. and Gouws et al. The previous works that involve wastewater recycle, treatment and reuse within (industrial) consuming processes dates back to 1970's. The critical need in reducing both contaminants and consumption of water and energy necessitate most of them, due to the fact that twenty percent of the world's total water consumption (this widely exceeds fifty percent in many industrialised countries) has been recently attributed to industries by UNESCO.
The scientific community has been largely involved in the topic of the design of optimal water networks in the last three decades, through minimizing both economic and environmental objectives. The design of Water Allocation Networks (WAN) is a complex task, especially when multiple contaminants are treated in the same plant with particular emphasis on the decision about the use of many regeneration units. This problem has been identified in previous works (e.g. Gunaratnam et al., Feng et al., Boix et al.) and formulated as a generic framework considering one or several objctive functions. The analysis of the dedicated literature shows that a robust approach that can take into account large problems is far from being straightforward. Also, the definition of constraints or assumptions must be specified and adapted to a case study, thus hindering the development of a standard approach. Although, the model-based optimisation approach allows handling of water network synthesis problems in their full complexity by considering representative cost functions, multiple contaminants and various topological constraints, it frequently presents major challenges of high computational burden to achieve optimality, and it does not guarantee global optimum which provides the lowest value (known as global minimum).
Some of the significant achievements in water network analysis that utilizes optimization-based modelling techniques and computational strategies are the work of Takama et al. [2] which provide seminal work on water network synthesis using optimization approach. Galan and Grossmann formulate optimization of distributed wastewater treatment network using mixed integer nonlinear programming. Zamora and Grossmann presented method for obtaining global optimization solution of water network synthesis. Doyle and Smith proposed sequential optimization approach in finding the optimal solution. Huang et al; adopt a representation of fixed flow rate in the water network synthesis. Savelski M and Bagajewicz M [1,3] provide rigorous proofs for the necessary conditions of an optimal direct reuse/ recycle and formulation of mixed integer linear programming for single contaminant water network synthesis [1,3]. Koppol and Bagajewicz addressed the issue of uncertainty in the water network synthesis problems.
Moreover, Faria and Bagajewicz proposed a planning model and way of obtaining global optimum result with piecewise- affine relaxation enhanced with bound contraction and also consider pre-treatment for water network synthesis in their later work. Sujak et al. [4] creates a model for the design of optimal total water network (OTWN) [4]. Sharma and Rangaiah [5], proposed designing, retrofitting, and revamping water networks in petroleum refineries using multiobjective optimization [5]. Tan and Cruz apply stochastic optimization based technique in water network synthesis problems. Karuppiah and Grossmann proposed a piecewise-affine relaxation of non convex terms in the solution of water network analysis. Tan et al. consider membrane separation based water regenerators for total water network synthesis. Hong et al. [6] proposed simultaneous optimization of heat-integrated water allocation networks.
However, despite all the above mentioned significant achievements in water network analysis research that utilizes optimization-based modelling techniques and computational strategies there are some challenges in the issues of non convexity (which leads to the presence of multiple local optimal solutions), nonlinearity (which is due to considering regeneration technologies as nonlinear mixed with linear objective function), simultaneous optimization of the interactions of rigorous design models for wastewater treatment technologies and multiple water-using units, enabling faster numerical solutions, development of more meaningful optimization-based formulations, uncertainty (posed by the data obtained from the industry, the assumed parameters in analysis of the problems), alternative methods for optimization under uncertainty and extension to resource recovery systems. However, all the above challenges and uncertainties can be handled by using stochastic programming which is robust optimisation method. The use of stochastic programming like Genetic Algorithm (GA) can improve the potential future directions in water network analysis and assist in developing feasible, cleaner and more economic industrial water networks (IWN) that drastically reduced freshwater consumption as well as wastewater, and ensure reasonable costs and efficient productivity (Ramos et al.).
Inconsideration of the above, this paper developed a general framework for water (fresh and waste) allocation planning (WAP) that can be applied to different water allocation contexts e.g. oil refinery, food production, pharmaceutical etc, by considering multiple contaminants with and without regeneration. The WAP problem was solved using a combination of stochastic genetic algorithm (GA) optimization and hybrid function optimization method. The non-convexity and nonlinearity challenges are adjusted by using reproduction parameters of GA which includes Elite Count and Crossover fraction to obtain possible
solutions by the use of Population creation function that is constraint dependent. The optimization method handles interactions of rigorous design models for wastewater treatment technologies and multiple water using units simultaneously. The solutions and parametric values so obtained from a case study of three processes have been further compared with the existing literature values.
Methodology
Superstructure for integrated water network (IWN) allocation problem
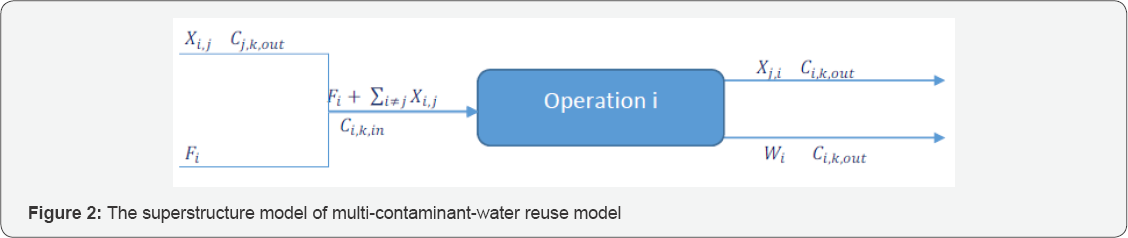
The superstructure model for IWN allocation problem as proposed by Ramos et al. is shown in Figure 1. It is generalization of the model given by karuppiah and Grossman and Ahmetovic and Grossmann [7]. The first part consists of freshwater source, water from regeneration units and from other process units all linked in to a mixer. This is followed by connection to different processes for further operation and addition of more contaminants strictly based on the acceptance level of contaminant concentrations of each process. The output water flow is linked to the splitter that separate flow in to discharge as wastewater, flow to regeneration units and to other processes. The second part starts with the mixer of water from process units and from other regeneration units link to further regeneration and passed to splitter which link the water flow to other process units and further regeneration units (Figure 1).

Formulising the water minimisation problem with and without regeneration
Multi-contaminant-water reuse without regeneration model
Fitness function: The fitness function for multi- contaminant-water reuse without regeneration model which is the sum of fresh water flow rates at the entrance of all water using processes is presented in equation1 (Figure 2).
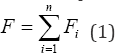
Where, F is the flow rate of freshwater entering operation in tons/h.
Constraints
Linear Constraints functions: The linear constraint function of the water mass balance of all processes involved in Multi contaminant water reuse is presented in equation 2.

Where, Xi ? is the flow rate of water reuse form to in tons/h, and
W is the wastewater flow rate out of the process in tons/h.
Nonlinear constraints functions
i. The nonlinear constraint function of the contaminant mass balance of all processes involved in multi-contaminant- water reuse is presented in equation 3:
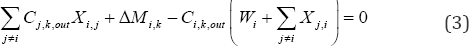
Where, c,,k is the average inlet concentration of contaminant to process in ppm.
ΔMjk is the average mass load of each contaminant for each operation in g/h.
i. The nonlinear constraint function of maximum contaminant inlet concentration involved in
multi-contaminant-water reuse is presented in equation 4:

Where, Cj,k,in is the average inlet concentration of contaminant k to process in ppm.
Cj,k,out , is the average outlet concentration of contaminant k to process in ppm.
Multi-contaminant water reuse with regeneration model
Fitness function: The fitness function for multi-contaminant water reuse with regeneration model which is the sum of fresh water flow rates at the entrance of all water using processes is as presented in equation 1: (Figure 3).

Constraints
Linear Constraint functions: The linear constraint function of the water mass balance of all process involved in multi-contaminant- water reuse with regeneration is presented in equation 5.
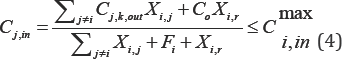
i. The nonlinear constraint function of the contaminant mass balance of all processes involved in multi-contaminant-water reuse with regeneration is presented in equation 6.
Where, Cok , is the average regeneration outlet concentration of contaminant in ppm.

ii. The nonlinear constraint function of the Maximum Contaminant inlet concentration involved in
multi-contaminant-water reuse with regeneration is presented in equation 7:

Where, all the symbols are as described in the first model description.
The main difference between multi-contaminant-water reuse with and without regeneration model is that the later has reconnection of water reuse after regeneration which includes the processes and streams connected to the regeneration unit, and the former has no regeneration that links to the processes and streams after use.
Solving the water minimisation problem using a GA Algorithm
For solving the equations above (1-7) the SOGA was used and in order to further improve the diversity and convergence of the solutions obtained by SOGA, a hybrid function was incorporated. The hybrid function "fmincon" is adopted to prevent the GA from getting stuck in the local minimum solution of the WAP. "Fmincon" uses a Hessian as an optional input.
Initial generation of chromosomes: The initial chromosomes were randomly generated by the Matlab software using boundary limits of all positive real values i.e Xu} > 0 . The binary values (1 and 0) of all the variables in each equation were identified. A value of 1 is assigned to the position of the variable if it exists in the equation and 0 otherwise. The values of contaminants were directly used in the equations as either the coefficient of the variable or as a constant.
Genetic algorithm in matlab:The SOGA is the basis used for solving the proposed optimization
model in Matlab, and in order to further improve the diversity and convergence of Pareto optimal solutions obtained by SOGA, a hybrid function is incorporated. The hybrid function works after the exhaustion of the combined crossover and mutation operator that improved the search ability of the algorithm.
Method for the hybrid approach: Incorporating a search method within a genetic algorithm can improve the search performance on the condition that their roles cooperate to achieve the optimization goal [8] (Tarek et al). The hybrid function "fmincon" is adopted to prevent the GA from getting stuck in the local minimum solution of the WAP. "Fmincon" uses a Hessian as an optional input. This Hessian is the matrix of second derivatives of the Lagrangian equation. The Hessian is the matrix of second derivatives of the objective function.
In single objective GA the hybrid function starts at the best point returned by the GA. The method involves combining principles of Genetic Algorithms (GA) and SQP algorithm that performs the computation of the Hessian of the objective function and its non-linear constraints. The hybrid function prevents the GA from being stuck in the local minimum solution of the WAP problem.
The Hessian for a constrained problem is the Hessian of the Lagrangian of an objective function f, nonlinear inequality constraint vector c, and nonlinear equality constraint vector ceq, the Lagrangian is given by equation 8.
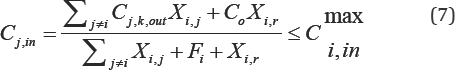
The are Lagrange multipliers.
The Hessian of the Lagrangian is shown in equation 9.

Matlab software provide SQP as "fmincon" which minimise constraint function based on a powerful concept in optimization known as trust regions. "Fmincon" uses a Hessian as an input function.
Key steps in waste water minimization for multiple contaminant problems
A number of key steps are to be followed for implementing a Wastewater minimization project [9].
Step 1: The need of waste water minimization identified based on limited availability of freshwater, economic and environmental regulation consideration.
Step 2: Data related to plant/industry is collected which include fresh water use by a particular unit, process quality requirement, cost and capability of treating water for initial input to the process and the wastewater generated in the end by the process.
Step 3: Drawing a flow sheet of the processes, which shows water balance diagram of the processes.
Step 4: Identification of the key contaminants for the processes; these are the contaminants that are to be reduced so that the discharged waste water can be reused or disposed under the specified control standards for an industry.
Step 5: The approach applied for solving the wastewater minimization problems. Mathematical programming approach: It involves definition of superstructure by considering each process within an industry to have a certain freshwater flow rate, output water from other process and or regenerated water, the output from the process will have effluent with certain level of pollutants concentration which can be discharged, recycled or regenerated for reuse, mathematical optimization and analysis of solution.
Step 6: After carrying out various analysis and calculations a Wastewater minimization project can be implemented.
Algorithm implementation
The basic flow chart for the implementation of Genetic Algorithm (GA) is shown in Figure 1. However, depending on the optimization software used in finding the solution, the steps may require a little adjustment in execution.
This paper uses Matlab software for implementing the steps; as such the following adjustments were adopted in obtaining the best result.
Steps in genetic algorithm implementation in Matlab:
a. Combining all variables in one vector.
b. Writing vector for lower and upper bounds ( lb and ub ).
c. Writing matrix and vector of inequalities ( A and b)
d. Writing matrix and vector of equalities ( Aeq and beq ).
e. Writing nonlinear constraint function.
f. Calling the solver: [x fval] = ga(fitnessfcn, nvars, A,b, Aeq, beq, lb, ub)
Algorithm testing
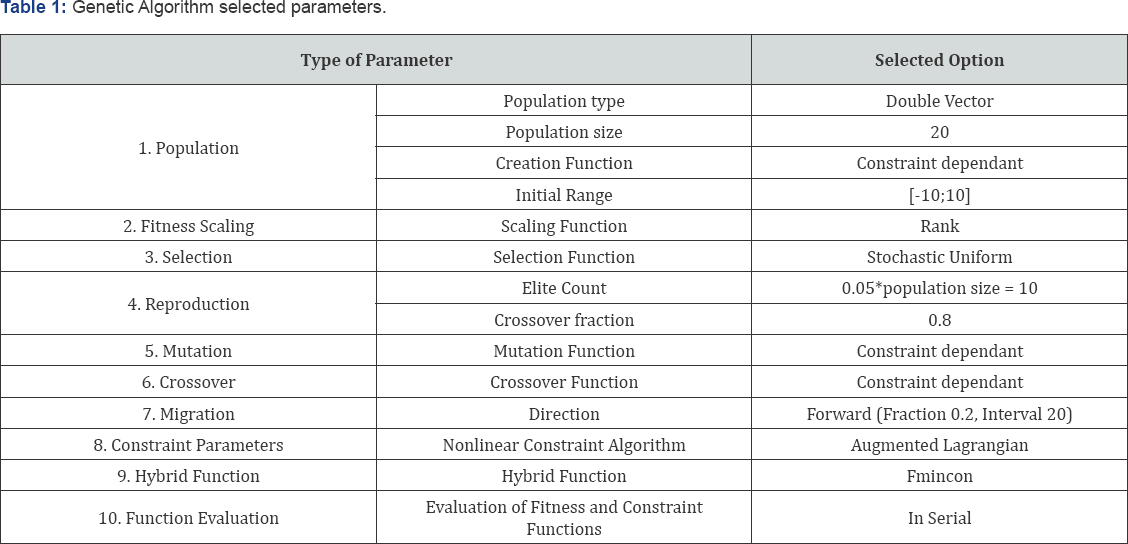
As the parameter setting that is good for one problem may not be suitable for another one sensitivity analysis of the parameters of the GA approach was done to identify the parameters that produce quality solutions [10,11]. In this research all parameters related to the implementation of the genetic algorithm were tuned before the algorithm is confirmed. These parameters are Population, Fitness Scaling, Selection, Reproduction, Mutation, Crossover, Migration, Constraint Parameters, Hybrid Function and Function Evaluation (Table 1). These parameters were chosen so that the optimal, or at least a good one, solution is found. Obviously, by the stochastic nature of Genetic Algorithm (GA), multiple runs on the same problem are necessary to get a good estimate of performance.
Furthermore, in order to verify the adopted methodology the solutions obtained have been further
compared with the existing literature obtained values.
Case Studies
The genetic algorithm program was used in two important examples in chemical engineering industries. The examined industrial cases have significant usage and discharge of fresh water and wastewater. The first case has three industrial processes and three contaminants but without regeneration. The second case is as the first case but with addition of regeneration.
Multi-contaminant water reuse without regeneration for 3 (Three) industrial processes
Considering an integrated optimization approach in multiple contaminant system that contains n operations, m contaminants, the numbers of variables involved are and there are equality constraints [12].
The Linear Constraint is derived from the water mass balance and the nonlinear constraint is derived from the contaminant mass balance and the maximum contaminant inlet concentration. The lower bound was set to zero to control all variable as positive numbers, while, the upper bounds was set to infinity.

Case Study: Input limiting process data The example data used have three process units and three contaminants, is fMann and Liu [13], with the limiting water data for the industrial process units shown in Table 2
Final points: Optimization terminated because the average change in the fitness value is less than function tolerance and constraint violation is less than constraint tolerance. The solution process further proceeds by switching to the hybrid optimization algorithm (FMINCON) and satisfy the constraints. "Fmincon" stopped because the size of the step is less than the default value of the step size tolerance and constraints are satisfied to within the default value of the constraint tolerance. FMINCON come to termination because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance. The final result is shown in Table 3.


The Superstructure representation of results for three (3) processes is shown in Figure 4. This shows the optimum water- using network for an example problem of multi-contaminant without regeneration-water reuse.
Solution of the problem corresponding to the diagrammatical Superstructure representation of the solution is shown in Table 4. It described the obtained result, indicating that the minimum total freshwater required by the industry is 70.0m3/h, 30m3/h for process 1 and 33.0m3/h for process 2 and 7.0m3/h for process 3. While, process 2 and 3 reuse 2.0m3/h and 21.0m3/h of wastewater respectively, from process 1.
Solution of the problem corresponding to the diagrammatical Superstructure representation of the solution is shown in Table 4. It described the obtained result, indicating that the minimum total freshwater required by the industry is 70.0m3/h, 30m3/h for process 1 and 33.0m3/h for process 2 and 7.0m3/h for process 3. While, process 2 and 3 reuse 2.0m3/h and 21.0m3/h of wastewater respectively, from process 1.
Multi-contaminant water reuse with regeneration recycle for 3(Three) industrial processes
Considering an integrated optimization approach in multiple contaminant system that contains n operations, m contaminants and regeneration units, there are 2n variables more than water reuse without regeneration. The numbers of variables involved are + 3n + nm and there are n + nm equality constraints [12].
The fitness function which is the sum of fresh water flow rates at the entrance of each water using process is as presented in equation 1.
Test problem: Input limiting process data: The example data used have three process units and three contaminants, and is taken from Mann and Liu (1999) and [13], with the limiting water data for the process units shown in Table 2 is used with the limiting water data for the process units shown in Table 2 is used with an assumed regeneration contaminant concentration of 25ppm:
Final points: Optimization terminated because the average change in the fitness value is less than function tolerance and constraint violation is less than constraint tolerance. The solution process further proceeds by switching to the hybrid optimization algorithm (FMINCON) and satisfy the constraints. "Fmincon" stopped because the size of the step is less than the default value of the step size tolerance and constraints are satisfied to within the default value of the constraint tolerance. FMINCON terminated. because the objective function is nondecreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance and the final result is shown in Table 5.


The Superstructure representation of result for three (3) the optimum water-using network for an example problem of processes with regeneration is shown in Figure 5. This shows multi-contaminant with regeneration-water reuse (Figure 6).

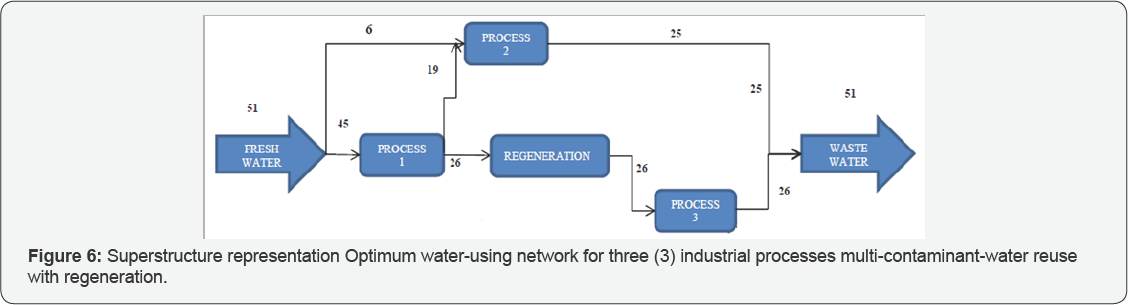

Solution of the problem corresponding to the diagrammatical Superstructure representation of the solution is shown in Table 6. It described the obtained result, indicating that the minimum total freshwater required by the industry with regeneration of 25ppm is 51.0m3/h, 45m3/h for process 1 and 6.0m3/h for process 2. Process 2 use additional 19.0m3/h of wastewater. While, process 3 reuse 20.0m3/h of wastewater only, from process 1 after regeneration.
Comparison of the obtained result with the existing literature value

Table 7 shows that the result obtained from the solution of multi-contaminant water reuse without regeneration for minimum freshwater consumption or wastewater generated is equal to that obtained from the literature. Moreover this study consider regeneration in the second case i.e multi-contaminant water reuse with regeneration with an assumption of 25ppm contaminant regeneration quality, while the literatures mentioned [13] (i.e Mann and Liu) did not find solution to that case.
Conclusion
The genetic algorithm has major advantages of flexibility and robustness as a global optimum result search method. Although, it uses stochastic optimization it can deal with highly nonlinear problems and on differentiable functions as well as functions with multiple local optima and is readily amenable to implementation, which renders them usable in real-time problems of WAP. The nonlinear programming solutions for multi-contaminant water network with and without regeneration are presented. The approach was based primarily on using MATLAB in implementing the genetic operators. A standard formulation was proposed that can be modified to suite a wide variety of WAP problems. The only data required are the number of processes, their associated maximum inlet and outlet concentrations, the mass load generated for each contaminant and the number of regeneration units with the corresponding efficiency related to each contaminant [14-23].
The best genetic algorithm parameters for obtaining a good result were presented, followed by the implementation. Finally the obtained results were compared with the literature values.
The model shows better result in considering multi-contaminant water reuse with regeneration.
Moreover, the future study will consider multi-objective optimization of water reuse network using multiobjective genetic algorithm capabilities of Matlab.
Acknowledgment
I would like to knowledge Petroleum Technology Development Fund (PTDF) Nigeria for funding this research.
References
- Savelski M, Bagajewicz M (2000) Design of water utilization systems in process plants with a single contaminant. Waste Management 20(8): 659-664.
- Takama N, Kuriyama T, Shiroko K, Umeda T (1980) Optimal water allocation in a petroleum refinery. Computers & Chemical Engineering 4(4): 251-258.
- Savelski M, Bagajewicz M (2001) Algorithmic procedure to design water utilization systems featuring a single contaminant in process plants. Chemical Engineering Science 56(5): 1897-1911.
- Sujak S, Shiun LJ, Alwi SRW, Manan ZA (2015) A model for the design of optimal total water network (OTWN).
- Sharma S, Rangaiah GP (2016) Designing, retrofitting, and revamping water networks in petroleum refineries using multiobjective optimization. Industrial and Engineering Chemistry Research 55(1): 226- 236.
- Hong X, Liao Z, Jiang B, Wang J, Yang Y (2016) Simultaneous optimization of heat-integrated water allocation networks. Applied Energy 169: 395-407.
- Ahmetovic E, Grossmann IE (2010) Global superstructure optimization for the design of integrated process water networks. AIChE Journal 57(2): 434-457.?
- El-Mihoub TA, Hopgood AA, Nolle L, Battersby A (2006) Hybrid Genetic Algorithms: A Review. Engineering Letters, 13:2, EL_13_2_11 Advance online publication.
- Dakwala M, Mohanty B, Bhargwa R (2009) A process integration approach to industrial water conservation: A case study for a starch industry. Dept of Chem Eng, IIT Roorkee, Journal of cleaner prod 17: 1654-1662.
- Yuan B, Gallagher M (2005) A hybrid approach to parameter tuning in genetic algorithms. In 2005 IEEE Congress on Evolutionary Computation 2: 1096-1103. IEEE.
- Singh SK, Srinivas C, Reddy BR, Ramji K, Naveen R (2014) 3rd International Conference on Materials Processing and Characterisation (ICMPC 2014) Sensitivity Analysis to Determine the Parameters of Genetic Algorithm for Machine Layout. Procedia Materials Science 6: 866-876.
- Prakotpol D, Srinophakun T (2004) GAPinch: genetic algorithm toolbox for water pinch technology. Chemical Engineering and Processing: Process Intensification 43(2): 203-217.
- Cao K, Feng X, Ma H (2007) Pinch multi-agent genetic algorithm for optimizing water-using networks.
- Alenazi M (2015) Genetic Algorithm by using MATLAB Program. Inter-national Journal of Advanced Research in Computer and Communication Engineering 4(11).
- Savelski M, Bagajewicz M (2003) On the necessary conditions of optimality of water utilization systems in process plants with multiple contaminants. Chemical Engineering Science 58: 5349-5362.
- Savelski M, Bagajewicz M (2000) On the optimality conditions of water utilization systems in process plants with single contaminants. Chemical Engineering Science 55: 5035-5048.
- Boix M, Montastruc L, Pibouleau L, Azzaro-Pantel C, Domenech S (2010) Multiobjective optimization of industrial water Networks with contaminants. Comput Aided Chem Eng 28(20): 859-864.
- Bagajewicz M, Savelski M (2001) On the use of linear models for the design of water utilization systems in process plants with a single contaminant. Trans IChemE Part A, Chem Eng Res Des 79: 600-610.
- Doyle SJ, Smith R (1997) Targeting water reuse with multiple contaminants. Trans IChemE Part B, Chem Eng Res Des 75: 181-189.
- Feng X, Bai J, Zheng XS (2007) On the use of graphical method to determine the targets of single contaminant regeneration recycling water systems. Chem Eng Sci 62: 2127-2138.
- Chaturvedi ND, Manan ZA, Wan Alwi SR, Bandyopadhyay S (2016) Effect of multiple water resources in a flexible-schedule batch water network. Journal of Cleaner Production 125: 245-252.
- Liu T, Gao X, Wang L (2015) Multi-objective optimization method using an improved NSGA-II algorithm for oil-gas production process. Journal of the Taiwan Institute of Chemical Engineers 57: 42-53.
- Yang M, Feng X, Liu G (2016) Algebraic approach for the integration of the hydrogen network with a single impurity. Industrial and Engineering Chemistry Research 55(3): 615-623.






























