Essential Spectrum of Internal Waves in the Ocean and Atmosphere: the Relation between the Frequency of the Induced Vibrations and Non-Uniqueness of the Limit Amplitude
Andrei Giniatoulline*
Department of Mathematics, Los Andes University, Colombia, South America
Submission: November 12, 2017; Published: February 19, 2018
*Corresponding author: Andrei Giniatoulline, Associate Professor, Department of Mathematics, Los Andes University, Bogota D.C., Colombia, South America, Tel: 5713394949, Fax: 5713324340, Email: aginiato@uniandes.edu.co
How to cite this article: Andrei G. Essential Spectrum of Internal Waves in the Ocean and Atmosphere: the Relation between the Frequency of the Induced Vibrations and Non-Uniqueness of the Limit Amplitude. Civil Eng Res J. 2018; 3(3): 555612. DOI: 10.19080/CERJ.2018.03.555612
Abstract
For various models of three-dimensional fluid which describe the flows in the Atmosphere and the Ocean, we find a relation between the essential spectrum of normal vibrations of internal waves and non-uniqueness of the limit amplitude of vibrations induced by external mass forces.
Keywords: Water Resources, Applied Ocean Research, Physical and Computational Models,Structural Dynamics, Internal Waves, Spectral Theory, Essential Spectrum, Limit Amplitude, Uniqueness of Mathematical Solutions.
Introduction
Let us consider a system of partial differential equations in x = ( x1 , x2, x3 )ϵ r3 of the following type:

Here,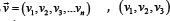 is a velocity field of the fluid, p (x, t) is the scalar field of the dynamic pressure,
is a velocity field of the fluid, p (x, t) is the scalar field of the dynamic pressure, 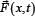 represents mass forces acting on the fluid, and A is a matrix operator which defines the specific model.
represents mass forces acting on the fluid, and A is a matrix operator which defines the specific model.
For example, in the model of rotational motion of the Earth over the vertical axis, the operator A takes the form
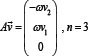
For the model of stratified fluid with exponentially decreasing density in the gravity field, the operator A is actingn on 4-dimensional vector: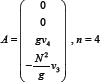 and is the dynamic
A = gv4 , n = 4 density of the fluid.
and is the dynamic
A = gv4 , n = 4 density of the fluid.
For the model which counts with salinity and heat transfer, the operator A acts on 5-dimensional vector:

and is the temperature of the fluid, while is the salinity.
In the considered problems, almost always, without loss of generality, the operator A may be considered as a skew- symmetric matrix.
We would like to analyze and to compare the results of the following two problems.
First, we consider the Cauchy problem for the system (1) for the case when the right-hand side 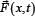 depends on time harmonically, i.e.,
depends on time harmonically, i.e., 
From the physical point of view, for this case, the solution of the Cauchy problem should stabilize and describe the mode of the induced vibrations with frequency .
Secondly, we consider the following problem of the normal vibrations for homogeneous system (1) associated with the Dirichlet boundary conditions 
In this way, the term  transforms into —λ , which permits the representation of the homogeneous system (1) as M—λI = 0 . Thus, we obtain a spectral problem for the operator M.
transforms into —λ , which permits the representation of the homogeneous system (1) as M—λI = 0 . Thus, we obtain a spectral problem for the operator M.
We would like to compare the spectrum of the operator M and the uniqueness of the limit amplitude of the induced vibrations for the Cauchy problem.
Results and Discussion
For the Cauchy problem, in [1] there was proved the following result for the rotational motion.
Theorem 1: Let the exterior mass force be a periodic function with frequency w ≥ 0 :

Then, the solution v(x,t) of the Cauchy problem is also periodic and the stabilization property is valid :
 is the solution ofthe stationary system with the external force .
is the solution ofthe stationary system with the external force .
We observe that for the case of the stratified fluid, the Theorem 1 was proved in [2].
Let us recall that, for a linear self-ad joint operator M acting in a Hilbert space, the essential spectrum is defined as the set of points of the continuous spectrum, limit points of the point spectrum, and eigenvalues of infinite multiplicity [3]. Therefore, t
he spectral points outside of the essential spectrum may only be eigenvalues of finite multiplicity.
For various types of the operator A, in [4,5] the following result was proved.
Theorem 2: There exists a finite constant , which is uniquely determined by the matrix , such that for the problem of normal vibrations, the essential spectrum of the operator is the interval of the imaginary axis :

Now, we would like to compare the relation between the uniqueness of the above limit amplitude of the induced vibrations of frequency , and the structure and localization of the essential spectrum of the normal vibrations.
The following result was proved in [6] for the rotational model, and later in [2] it was proved for the model of stratified fluid.
Theorem 3: If the frequency w of the exterior mass forces does not belong to the essential spectrum of the normal vibrations, then the limit amplitude  is unique. On the other hand, if, however, the frequency w belongs to the essential spectrum
is unique. On the other hand, if, however, the frequency w belongs to the essential spectrum  , then the limit amplitude loses the uniqueness. From the physical point of view, it means that the resonance effect takes place.
, then the limit amplitude loses the uniqueness. From the physical point of view, it means that the resonance effect takes place.
We also would like to observe that, particularly, the explicit example of non-uniqueness of the solution may be found in [4] for the construction of the Weyl sequence [7] in the proof of the result for the essential spectrum.
Conclusion
The remarkable relation between the essential spectrum of normal vibrations and non-uniqueness of the limit amplitude may explain the effect of resonance of internal waves from a new mathematical point of view. May we also express a conjecture that similar results are valid for more general types of the operator A.
References
- Maslennikova V, Kumar P (1986) Stabi- lization and the limiting amplitude of the Cauchy problem for non-homogeneous Sobolev systems. Siberian Mathematical Journal 27 (3): 142-153.
- Giniatoulline A, Mayorga E (2011) On the existence, uniqueness, stabilization and limit amplitude for non-homogeneous system modelling internal non-stationary waves in stratified flows. Pacific Journal of Applied Mathematics 3(4): 19-37.
- Kato T (1966) Perturbation theory for linear operators. (1st edn), Springer-Verlag, Berlin, Germany.
- Giniatoulline A (2005) An introduction to spectral theory. (1st edn), R.T. Edwards, Philadelphia, USA.
- Giniatoulline A (2015) On the spectral properties of incompressible rotating stratified fluid. Asian Journal of Mathematics and Computer Research 2(2): 63-73.
- Maslennikova V, Giniatoulline A (1988) Spectral properties of operators for the systems of hydrodynamics of a rotating liquid and non-uniqueness of the limit amplitude. Siberian Mathematical Journal 29: 812-824.
- Riesz S, Sz-Nagy B (1979) Functional Analysis. (1st edn), Frederik Ungar, N.Y., USA.






























