Numerical Analysis of Stressed State of an Elastic Strip Plate with Collinear Cracks and Thin-Walled Inclusions at Antiplane Shear Loading
Ali Golsoorat Pahlaviani*
Department of civil, central tehran branch islamic azad university, Iran
Submission: October 3, 2017; Published: January 17, 2017
*Corresponding author: Ali Golsoorat Pahlaviani, Central tehran branch islamic azad university, Iran, Email: ali.golsoorat_pahlaviani@iauctb.ac.ir
How to cite this article: Ali Golsoorat Pahlaviani. Numerical Analysis of Stressed State of an Elastic Strip Plate with Collinear Cracks and Thin-Walled Inclusions at Antiplane Shear Loading . Civil Eng Res J. 2017; 3(1): 555605. DOI: 10.19080/CERJ.2018.03.5555605
Abstract
In this paper, a long elastic strip plate with collinear cracks at antiplane deformation in the case that each crack tips are joined by thin- walled inclusions deformed according to the known Winkler's model is considered. The uniformly distributed shear forces causing the antiplane deformation of the plate are acting on the horizontal sides of the strip and the edges of cracks are free of inclusions. For convenience in numerical calculation the strip plate is divided to several plates so that each segment has one crack at the center. The solution of the stated problem via Fourier sine transformation is reduced to singular integral equation (SIE), and, consequently, to a system of linear equations. Numerical calculations based on the Gauss Quadratic solution are achieved. For the main characteristics of stated problem, such as the SIF, the crack opening, the shear stresses on the edges of the inclusion, and the shear stresses out-of-crack the obvious equations are obtained and the special cases considered.
Keywords: Numerical analysis; S.I.F; Tip inclusions; Anti-plane Shear; SIE
Introduction
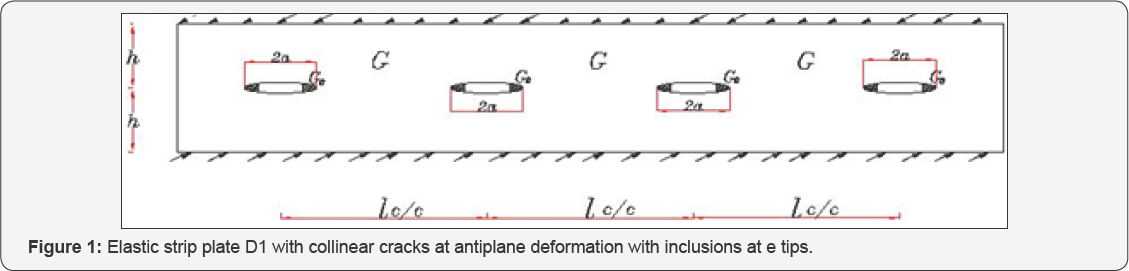
In this paper, we calculate the stress distribution state and S.I.F of the crack tips and dislocations of edges of a long strip elastic rectangular plate (Figure 1). The stress Intensity is essentially decreasing the known strength and durability of structural members and engineering parts. For this reason, the necessity of theoretical investigation of stress concentration zones and the development of the methods which decrease the stress intensities is occurred. One of these methods was proposed in [1], the edges of linear finite crack of elastic infinite plate at the end areas are joined via thin-walled inclusion in the shape of continuously distributed linear and nonlinear deformed springs, meanwhile, the plate is subjected by uniformly distributed tensile remote stress perpendicular to the central line of crack. Taking into account the above-mentioned physical model of inclusions and based on assumptions in [24], the valuable decrease of stress intensity factors (SIF) at the end points of crack can be achieved by the appropriate selection of elastic and geometric characteristics of problem, and this can prevent the crack propagation. Applying Fourier finite sine transformation, the solution of stated problem can be reduced to the solution of singular integral equation (SIE), and, consequently, via the known method [5-7], the solution of singular integral equations can be reduced to the system of linear equations. For the main characteristics of stated problem, such as the SIF, the crack opening, the shear stresses on the edges of the inclusion, and the shear stresses out-of-crack on the line of its location, the obvious equations are obtained, the special cases are considered and for various materials the decreasing trend of S.I.F based on the various shear modulus were shown.
Governing Equation of Boundary Value Problem
Following the approach represented in [1] consider a prismatic elastic body with a rectangular cross-section in Cartesian coordinates Oxyz occupying an area Ω = {-∞≤x≤∞; -h ≤ y ≤ h; -∞< z <∞} and possessing a shear modulus G . The prismatic elastic body is rigidly clamped by the vertical edge x = -∞ and x = +∞ , and loaded by the shear forces equal to T (x) acting both in positive and in negative directions of Oz -axis at the horizontal y = ±h . Furthermore, on the symmetry plane y = 0 , the body Ω has several through-in-thickness cracks each in a shape of strip with length 2a on plane y = o and -∞< z <∞ at distances equal to 𝓁 (α < 𝓁/2). The shear forces of equal intensities T0 (x) are acting in opposite directions of Oz-axis on the upper (+) and lower (-) areas of edges ω±={y = ±0; 𝓁/2-b < xi < 𝓁/2 + b; -∞< z <∞ } (b <a) of the crack. Besides that at the ending areas
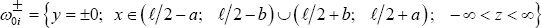
The edges of the crack are joined by the thin-walled inclusions with the shear modulus G deforming by the Winkler model. Let's assume that the prismatic body Ω subjected to the above-mentioned shear forces is in a state of anti plane deformation in the direction of Oz-axis on the basic plane Oxy . The main rectangle D1 = {-∞≤ x ≤+∞; - h ≤ y ≤ h} with several cracks ω ={y = 0; 𝓁/2 - α < xi < 𝓁/ 2 + α} (0 < α<𝓁/ 2) is cross-section of the body Ω with the plane located on this plane Oxy (Figure 1).
It is necessary to determine the dislocation density on the crack edges, SIF, the crack edges opening, the shear contact stresses on the edges of the inclusion, and the shear stresses outside the crack on the line of its location. For convenience in numerical calculation the strip plate is divided to several plates so that each segment has one crack at the center (Figure 2).
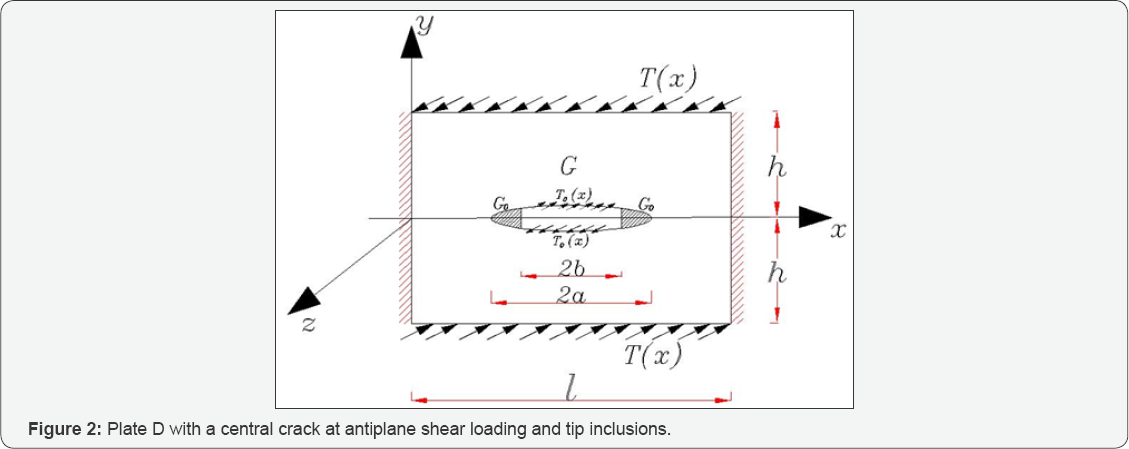
Now, let's derive the governing equations of the stated problem. For this purpose, it must be initially mentioned that the component uz = w (x, y) in the direction Ox-axis is the only non- zero component of displacement in the case of antiplane deformation, and harmonic function in the area D ω0. The components of shear stress τxz and τyz are the only nonzero components of stresses. Therefore, the problem can be mathematically stated as a boundary value problem in the following way:
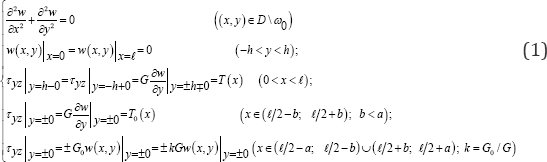
For of the determination of boundary value problem (1), the rectangle D is divided by Ox-axis onto upper D+={0 ≤ x ≤ 𝓁; 0 ≤ y ≤ h} and lower D-={0 ≤ x ≤ 𝓁; - h ≤ y ≤ 0} rectangles. The following supporting boundary value problems are considered for them.
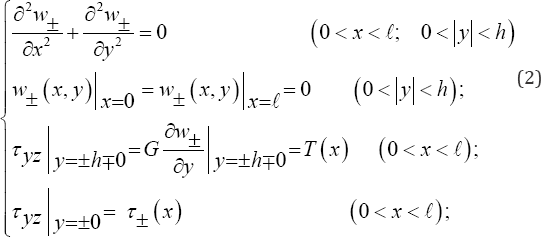
Where, the sign "+" and "-" are related to the rectangles D+ and D- , correspondingly.
τ( x) is the unknown fracture shear stress outside the crack ωa on the its line.
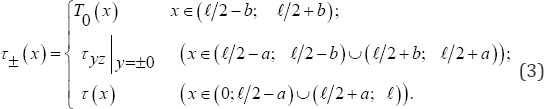
Taking into account the symmetry of stated problem with respect to -axis
ω+ (x, y) = -w_ (x, y) (0 < x < 𝓁); τ+ (x) = τ_ (x) (0 < x < 𝓁); (4)
Consequently, the determination of supporting problem (2) for the rectangle D+ can be considered only. Based on the reference [8], the above-mentioned problem can be determined via Fourier finite sine transformation on the variable x .

Multiplying by sin(xnx/𝓁) both sides of the differential equation and the border conditions of (2), and integrating it from 0 to 𝓁 , Fourier finite transformation (5) can be applied to the boundary value problem (2) for D+ . The boundary value problem in Fourier transformations can be obtained after the simple reductions.

The Singular Integral Equation
After some simple transformations and calculations according to [1] and [9-11] the following equations can be derived:
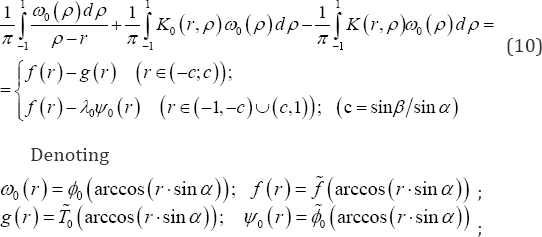

The first integral of equation (10) for ρ=r is assumed as a main value of the Cauchyfs relations. Meanwhile, Tn(x) and Un-1(x) are Chebyshev polynomials of the first and the second kind,
Finally, the stress intensity factors at the end points (a1;b1) of the crack can be expressed by the following equations:
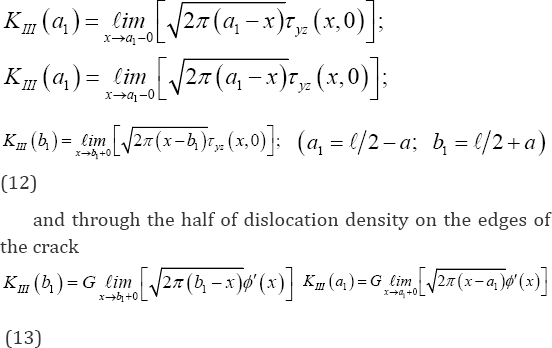
Gauss Quadrature Method
Now, as it was mentioned above, the determinative singular integral equations (S.I.E) (10) can be reduced to a system of linear equations and following to the approach represented in [1], the determinative S.I.E (10) can be reduced to the system of Algebraic linear equations as follows:
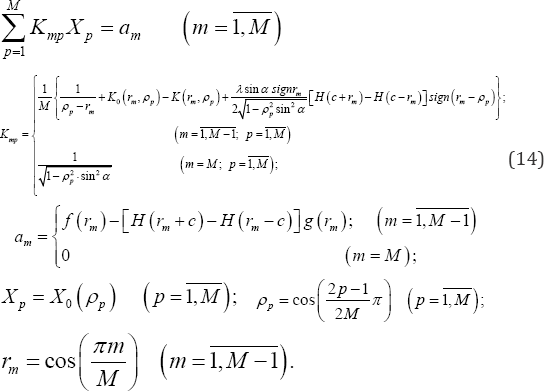
Where M is an arbitrary natural number, rm and ρp are the roots of Chebyshev's polynomials of the first kind Tm (ρ) and the second kind UM-1 (r)
The main physical characteristics of the stated problemcan be expressed by the determination of the system of linear equations (14). The plate shear stress out of the crack at the interval y=0 ,x ∈ (0,𝓁 /2-α)∪(𝓁/2 + α,𝓁) can be obtained as below:

For the dimensionless shear stresses on the edges of inclusion applying equation (20), the following equation can be derived
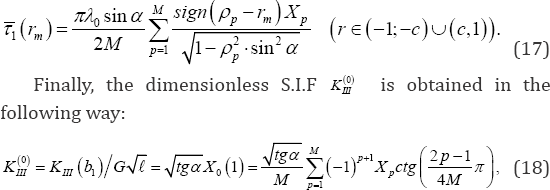
Where,X0(1) the value is applied through the Lagrange interpolation coefficients based on Chebyshev's polynomials. Therefore, solving of the system of linear equations (14), the main physical characteristics of the stated problem can be expressed by equations (15)-(18).
Numerical Calculation
For numerical calculations we consider a special case of the loading of the rectangular plate. For this case, the crack edges are free of shear forces, and shear concentrated force acting on the horizontal sides of rectangular plate:
T0 (x)≡ 0, T (x) = Pδ(x - 𝓁/2),
Where, δ(x) is a certain Dirac Delta function. In this case g(r)≡0, in (11), as well as, with respect to equation (8), the following equation has been obtained
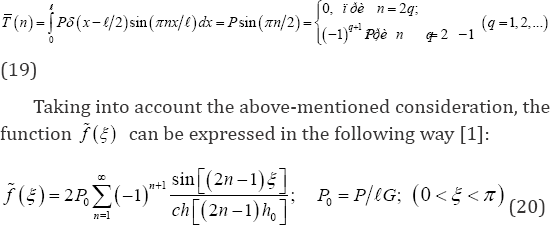
And the function f(r) from equation (11) can be obtained in the following way
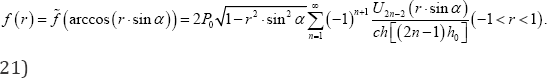
It is obvious that the function ω0 (r) with respect to the symmetry of line x = 𝓁/ 2 in this special case, and, consequently, the function x0 (r) according from equation (14) are odd functions, therefore, the components of the second integrals in equations (10) and (15) containing polynomials r or t in arguments tend to zero, so that, the above-mentioned equations and the kernel-matrix Kmp of system of equation (14) are simplified .and the expressions of functions 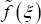 and f (r) are from equations (20)-(21). The numerical analysis of the main characteristics of stated problem can be carried out for
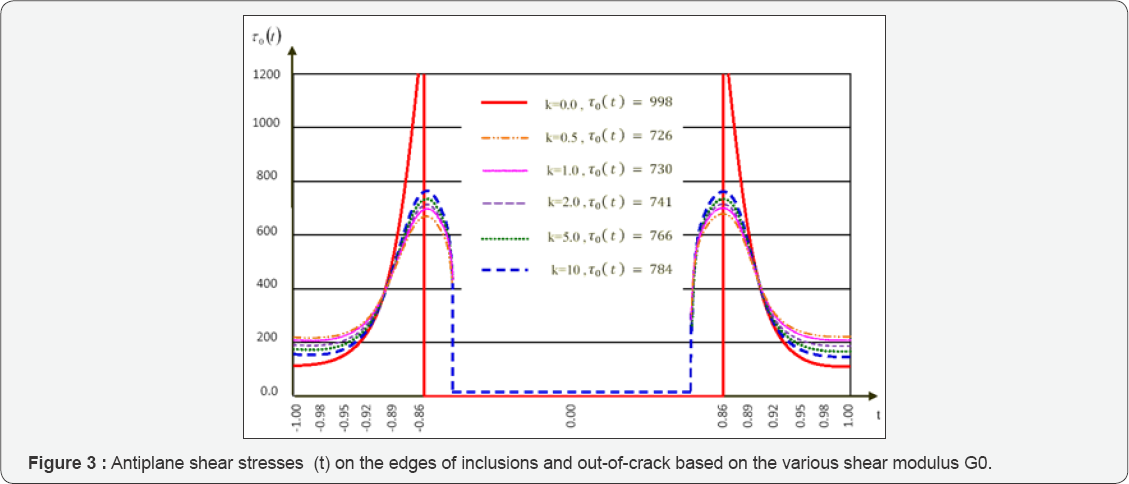
the considered special case. Antiplaine shear stresses τ0 (t) on the edges of inclusions and out of crack based on the various shear modulus GO were calculated and shown in (Figure 3) also
decreasing dislocation of crack edges due to inclusions tip repair are shown in (Figure 4).
and f (r) are from equations (20)-(21). The numerical analysis of the main characteristics of stated problem can be carried out for
the considered special case. Antiplaine shear stresses τ0 (t) on the edges of inclusions and out of crack based on the various shear modulus GO were calculated and shown in (Figure 3) also
decreasing dislocation of crack edges due to inclusions tip repair are shown in (Figure 4).
Conclusion
Numerical calculations show that the repair of crack tips causes avoiding the singularities and reduces the anti-plane S.I.F KIII , about 50 percent, also for strengthen and stop the crack propagation near to region at the tips, it is not need to use a material with very high shear rigidity value G0 [12]. Meanwhile the crack opening C.O.D decreases about 50 percent, and in addition the shear stresses at the crack tips fall down near to 30 percent.
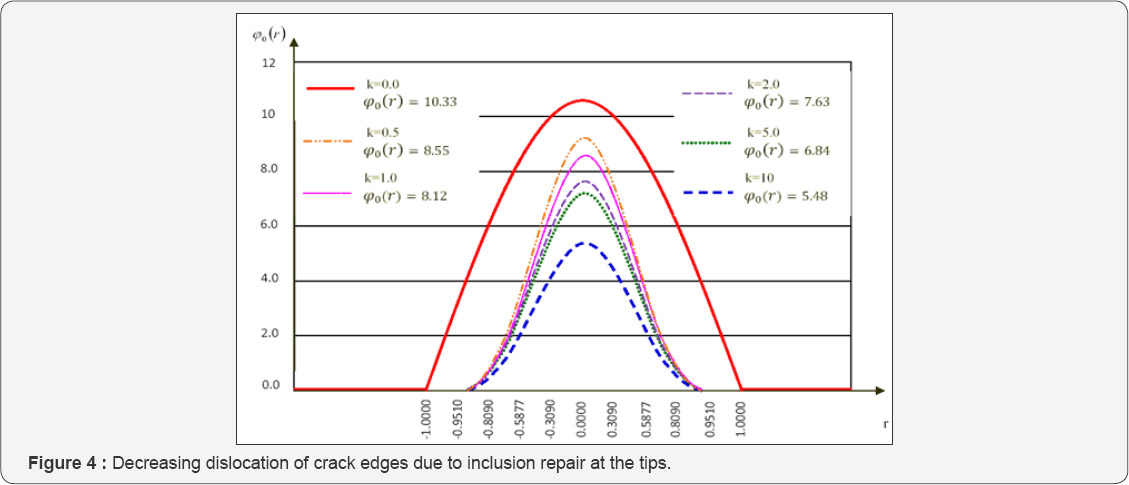
The linear Algebraic system of equation (14) were solved regarding to relations (19)-(21) for the special case of anti-plane shear loading for several metals on a base metal steel for the main plate [13]. The shear moduli of the metals over the steel shear modulus are represented as a ratio on the horizontal axis in (Figure 5).
The stress intensity factors S.I.F K III that are very important and show the intensity or index of upper limit of shear stresses magnitude calculated through the equation (18) that are shown in (Figure 5), which presents the decreasing trend of S.I.F curve when the ratio of k=G0/G goes up. It also shows that the crack tip repairing by adding another material at the tips to prevent crack propagation, can reduce the S.I.F about 50 percent, means this approach is very effective to avoid the crack propagations in cracked plates, mathematically is a treatment for well-known singularities at the crack tips, defects and holes.
References
- Mkhitaryan SM, Pahlaviani Ali Golsoorat (2011) Stressed state of an elastictangle with a central and thin - walled inclusions at antiplane deformation, The 3rd International contemporary problems in architecture and construction Beijing, conference proceedings, china.
- Rose LRF (1987) Crack reinforcement by distributed springs 35(4): 383-405.
- Mkhitaryan SM, Bardzokas Theocaris PS (2009) DI Reinforcement of a cracked infinite elastic plate with defects. Symposium on Recent Advances in Mechanics, dedicated to the Late Academician, Athens, Greece, p. 49-50.
- Bardzokas DI, Mkhitaryan SM (2010) About the interaction of a periodic system of cracks in a infinite elastic plate with the thin- walled defects kind of indefinitely distributed springs. Proceedings, 2nd international conference "contemporary problems in mechanics of continuum media, Delijan, Armenia 1: 133-137.
- Erdogan F, Gupta GD, Cook TS (1973) The numerical solutions of singular integral equations. Methods of Analysis and Solution of Crack Problems, Noordh off Intern, Leyden.
- Theocaris PS, Iokimidis (1977) NI Numerical Integration Methods for the Solution of Singular Integral Equations. 35(1): 173-185.
- Panasjuc VV, Savruk MP, Datsyshin AP the stress distribution in the neighbourhood of cracks of plates and shells. Kiev.
- SneddonI (1951) Fourier Transforms. New York, Toronto, London.
- Mkhitaryan SM, Pahlaviani Ali G (2010) The Stress Distribution Field of Piecewise Homogeneous Elastic Rectangular Plate With a System of Collinear Cracks Subject to Antiplane Deformations. 2nd international scientific and technical conference Architecture and Construction- Contemporary Problems, Yerevan Jermuk, conference proceedings 2: 295-303.
- Pahlaviani Ali G (2010) Main Characteristics of Fracture Failure of a Piecewise Homogeneous Elastic Plate with Crack Subject to Antiplane Deformations. 2nd international scientific and technical conference Architecture and construction contemporary problems , Yerevan- Jremuk, conference proceedings 2: 304-310.
- Alexandrov VM, Mkhitaryan SM (1983) Contact problems for bodies with thin lovers and layers. Moscow, Nauka, pp. 488.
- Murakami Y (1987) Stress intensity factors handbook Editor in chief (1) Pergamon Press.
- Bardzokas DI, Gevorgyan SKh and Mkhitaryan SM (2005) About a stress deformation condition of a piecewise uniform wedge with a system of collinear cracks at an antiplane deformation Mathematical Problems in Engineering, USA, pp. 245-268.






























