Abstract

To increase trial efficiency and shorten development timeline, two-stage phase II/III seamless inferential designs are often applied to new drug development programs. For such a design, multiple active treatments (doses) and a control are included in stage 1 (phase II). At the end of stage 1, one or more active treatments with the largest observed treatment effects are selected for stage 2 (phase III) unless there is sufficient evidence that the trial should be stopped early due to unexpected futility or strong treatment effects. If the trial is continued to stage 2, data of the two stages will be combined for the final inference. To control the type I error rate, the test statistics based on data of stage 1 should be adjusted for multiplicity then combined with the test statistics of stage 2. The commonly used pre-specified weights for combining the statistics of the two stages are the square roots of the proportions of the pre-planned sample sizes of the two stages of the selected treatments, which ignores the multiplicity of the treatment selection. In this research, we explore potentially more efficient adjusted weights for different multiplicity adjustment methods. We also consider trial adaptation for the desired conditional power for the adjusted weights. Simulations are conducted to evaluate the performances of different weight adjustment methods.

Keywords:Seamless design; weighted combination test; closed test procedure; estimation of treatment effect; conditional power; early efficacy claim.

Introduction

To increase trial efficiency and shorten development timeline, a two-stage phase II/III seamless/adaptive design with multiple treatments in stage 1 may be applied to a clinical trial [1,2]. With the seamless design, the trial can be stopped early at the end of stage 1 if all treatments (doses) are futile or at least one of the treatments (doses) shows unexpectedly strong treatment effect for an early claim. Otherwise, based on stage 1 results, promising treatments (doses) will be selected for further study in stage 2. We can also conduct trial adaptation including sample size adaptation for stage 2 based on the desired conditional power for the final analysis. To control the type I error rate, multiplicity adjustment [3] for the treatment selection at stage 1 is necessary for the test statistic derived based on data of stage 1. The multiplicity adjustment will make the adjusted p-value relatively larger or equivalently the variability larger. To combine data of the two stages for the final inference, a weighted combination method is often employed. The commonly used pre-specified weights are the square roots of the proportions of the pre-planned sample sizes of the two stages [4] regardless of the numbers of treatments in the two stages. Clearly, such weighting approach may put too much weight on the adjusted test statistic of stage 1. The question is then whether adjustment on weights is more preferrable and potentially increases the power for treatment effect assessment.

Different methods such as Bonferroni, Dunnet, Hommel (Simes) and Sidak methods [5-8] can be applied for multiplicity adjustment. In this research, we consider the corresponding adjusted weights for these methods. Evidently, these adjusted weights put relatively smaller weights on the adjusted stage 1 test statistics. We will use simulation to show whether weights have a big impact on the power for the combination test. The rest of the paper is organized as follows. In Design and methods, we discuss the two-stage design, the methods for multiplicity adjustment and the corresponding adjusted weights for the weighted combination test which combines data from the two stages. In Initial sample size and power consideration and Adaptive design, we consider the appropriate initial sample sizes for stage 1 and the whole study based on certain assumptions so that the probability of false early futility stopping is not too large and the overall power for eventually detecting the treatment effect is not too small. If the conditional power for the final analysis is small, sample size adaptation may be performed for stage 2. In Calculations and simulations, we present the simulation results that demonstrate the impact of weights on power. We then conclude the paper with brief discussion in Discussion.

Design and methods

In the following derivations, we assume the seamless study has two stages. In the first stage, there are I active treatments and a placebo control. The I active treatments could be different doses of the same drug but could also be different drugs (in an umbrella trial setting). An interim analysis is performed at the end of stage 1 to make early futility assessment, efficacy claim and/or treatment selection for stage 2. If the I active treatments are different doses of the same drug, we may only select one dose or at most two doses (in case the higher dose has safety issue based on the overall data) for stage 2. Nonetheless, it is possible that all I active treatments may be kept for stage 2 if they are different drugs. To simplify the discussion, we assume that the endpoint is continuous and follows a normal distribution.

Suppose endpoint variable for patient j(=1,...,n_ik)in treatment group i (=0 for placebo and =1, …, I for the active treatments) and k^th analysis (=1 for the interim analysis, =2 for the final analysis) Y_ijk ~ N(μ_i σ²)where 2σ is assumed to be known or estimated with a high level of precision. Here, we allow sample size n_ik to be different across treatments for an unbalanced design. If active treatment i is dropped or declared efficacious after the interim analysis, n_i2=0. The significance level for early efficacy claims for treatment i is α_i1. If we expect very small power for the interim analysis for treatment i, particularly when the I treatments are different drugs, to reserve more significance level for the final analysis or to have more safety data, we may set α_i1=0.

For greater flexibility, selection of treatments for stage 2 will be based on nonbinding criteria which are not factored into the type I error rate calculation. Data of the two stages of the selected treatments may be combined in an appropriate way for the final inference at the end of stage 2. The significance level for the final analysis is derived for controlling the overall type I error rate to be α for the entire study (for an umbrella trial, we may not need to control the type I error rate across different drugs, in that case, we may just control the type I error rate within each drug.We then can apply the regular seamless design to individual drugs and no multiplicity adjustment across drugs is necessary. If we do need to perform adjustment based on request from regulatory agencies, the methods proposed in this manuscript can be employed.

Let .The null hypothesis under consideration is .Suppose is the estimator (e.g., the between-treatment difference of sample means) of δ_i and the corresponding variance based on data of stage k. Then The nominal/unadjusted p-value for H_0i is

Where Φ(⋅) is the cumulative distribution function of the standard normal distribution. The correlations among the test statistics within a stage are positive. For a balanced design, correlation coefficients among all ’s and among all ’s are 1/2 as they share the same control-arm response estimate.

As in Bretz et al [4], a closed testing procedure [9] can be applied to control the overall type I error rate. For a one stage setting, the procedure can be described as follows:

• For the set of elementary null hypotheses: , construct intersection hypothesis .

• Let p_j denote the adjusted p-value for H_0I

• Reject an elementary null hypothesis H_0i if all the valid adjusted p-values p_j for H_0I with i ∈ I⊆I₁ are smaller than the defined significance level.

An adjusted p-value p^A _i1 for multiplicity and the interim analysis can be derived (see below). If p_i1 ^A ≤ α_i1, H_0i will be rejected at the interim analysis and an early efficacy claim can be made for treatment i. Let I₂ ⊆I₁ denote the index set of hypotheses that have not been rejected and accepted at stage 1 and will be tested at stage 2. A treatment claimed to be effective or dropped due to futility at stage 1 has no data at stage 2 and therefor is not included in I₂. The adjusted p-value p_2I of stage 2 for an intersection hypothesis H_0I is Suppose p_1I and p_2I are the stagewise p-values for H_0I. Note that multiplicity adjustment for H_0I is made within each stage separately which can be performed using any standard multiple testing procedure. We then use a pre-specified combination procedure to combine information from the two stages for the final analysis if the null hypothesis has not been rejected or accepted (based on futility criterion) at stage 1. There are many combination approaches. We will focus on the weighted combination test [10-12] in the following. For the pre-specified weights w₁ and w₂ such that , the weighted inverse normal combination p-value for the stagewise p-values p₁ and p₂ from the 2 stages is

Bretz et al [4] use weights and which are the square roots of the proportions of the sample sizes of the two stages for (1). These are the efficient weights when I=1 and no sample size adaptation is performed for stage 2. They are equivalent to the weights of a classical two-stage group sequential design and allocate equal weights to individual patients. However, they may not be efficient when I>1 due to the multiplicity adjustment. For example, suppose there are I active doses and placebo control in stage 1, the observed best dose, say dose 1, is selected for stage 2 and the other doses are dropped after the interim analysis. If we use a Bonferroni multiplicity adjustment for the familywise type I error rate control for stage 1, the adjusted p-value will be which can be used to test any intersection hypothesis H_0I containing H₀₁. Since there is only one dose for stage 2, there is no need for multiplicity adjustment for the p-value of stage 2, and we can directly use p₁₂ in (1) for forming the test statistic of the final analysis

Clearly, if is used where n₁₁ is the pre-planned sample size of stage 1 and n₁₂ is the one of stage 2 in the case of a balanced design for dose 1 and placebo, we may put too much weight on the statistic of stage 1 and potentially reduce the power. Moreover, if a sample size adaptation is performed for stage 2, the actual sample size for stage 2 may be larger than n₁₂. Therefore, intuitively, such a w₁₁ seems too large even when there is only one active treatment initially. We will explore whether some pre-planned adjustments, at least for the multiplicity, may provide more preferrable choices of w₁₁.

If the amount of information for the interim analysis is sufficient to avoid a big chance of selecting a wrong dose, stage 1 p-value for the selected dose should not be large. Thus, for the selected, for example, dose 1, likely, . If the observed treatment effects for the interim and final analysis are consistent , for the p-value of the regular final test to be smaller than 0.025,

If the sample size for the interim analysis is half of the total sample size (n_i1=n_i2), the test statistic for the interim analysis would be

and . Since I will not be larger than 5 in general, should hold. We can also use conditional power concept to argue that if dose 1 is selected for stage 2. Let z₁ be the adjusted observed test statistic at the interim analysis after the adjustment for multiplicity for stage 1, then

and

Suppose the estimate of treatment effect in z₁ is still (the numerator), from (3), the corresponding adjusted standard deviation (the denominator) should then be

Clearly, σ_AB11 may contain estimate which will be discussed and addressed later. Only when I=1 or there is no multiplicity at stage 1, will σ_AB11 be the same as σ₁₁. With (4), (2) becomes

where is stochastically smaller than . The test statistic for the final analysis combining data from the 2 stages with multiplicity adjustment is

which should be compared to the regular critical value z_α12 for the final analysis with significance level α₁₂ which will be discussed later. To maximize under constraint and , the weights should be

For the special case where I=1, and , and ; therefore, and . For I>1, as , .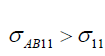

The adjusted approach put less weight on the test statistic of stage 1 due to multiplicity, which may also be preferable when we conduct a sample size increasing adaptation for stage 2.

In (4), when I>1, σ² _AB11 involves parameters and estimate of treatment effect at the interim analysis. These will not be available at the design stage when we need to pre-specify the weights. We will use where δ₁ and σ² in are the assumed values for the parameters for trial design (e.g. to properly power the corresponding fixed two-arm design).

With the pre-specification of the weights, the significance level for the final analysis after spending α₁₁ for the interim analysis and the only selected dose 1 will be derived based on

where (Z₁,Z₂)' follows a bivariate normal distribution with mean 0, variance 1 and correlation w₁₁. Note that in (5), and are independent, but with the multiplicity adjustment is stochastically smaller than Z₁. Thus, if , we claim efficacy early at the IA with alpha spending of α₁₁. Otherwise, if , we claim the treatment effect at the final analysis with the overall type I error rate controlled at level α when dose 1 is the only dose selected for stage 2.

In the scenario where we need to select two doses for both efficacy and safety considerations, multiplicity adjustment should also be performed for stage 2. Suppose a Bonferroni approach is again applied, (2) then becomes

for the two selected doses (say i=1 and 2). In (7), regardless of the number of doses in stage 1, since only two doses are selected for stage 2, the corresponding Bonferroni adjusted p-value is min(1,2)p_i2. Similar to the adjusted standard error for stage 1, the adjusted standard error for stage 2 and dose i could be

The weights for the analysis of dose i are

If we want to select more than 2 doses (or two drugs) for stage 2 for some considerations, we just need to do the corresponding Bonferroni adjustment for the data of stage 2 in (7).

Besides the Bonferroni adjusted p-value method, there are other less conservative approaches. Suppose are the ordered p-values for the I treatments of stage 1. For the case of selecting the treatment with the smallest nominal p-value (or the largest observed treatment effect) at the IA, the adjusted p-value for the Sidak test [8] is . The combination test becomes

where z₍₁₎ is the observed test statistic for the nominal p-value p₍₁₎₁. We may use

similar to (6) to derive the weights for the Sidak test. Since the Sidak test is more powerful compared to the Bonferroni test, the corresponding weight for the Sidak test for stage 1 should be larger than the one of the Bonferroni tests as shown in (Figure 1).

For the Simes test (1986), the adjusted p-value based on data of stage 1 for hypothesis is . If I=3, besides , the other adjusted p-values for the hypotheses which contain H_0{(1)} are , (larger than and . Only when all , , and are rejected at the nominal level, can be rejected in a closed test procedure [9] to control the overall type I error rate. Therefore, the adjusted p-value of the Hommel test [6] for testing at stage 1 is .

This adjusted p-values will be combined with the one based on data of stage 2 through (1) to test the corresponding hypothesis. It is not straightforward to specify the adjusted weights for this combination test given the complicated adjusted p-value of the Hommel test. Regardless, they should be somewhere between the two extremes of the adjusted weight of the Bonferroni test and the weight of no adjustment. A straightforward and simple selection is the mean or geometric mean of the two. The Hochberg test [13], a step-up approach, is slightly less powerful than the Hommel test and therefore are not considered here.

For Dunnet test [5], suppose Z_i1 are the test statistics and z_i1 are the observed values (i=1, …, I) of stage 1, the adjusted p-value for the selected dose say dose 1 is . The adjusted weights can be derived based on the adjusted standard deviation

through numerical computation. The Dunnet test is more powerful than the Sidak test because of the positive correlations among Z_i1’s which have the same distributions under the null hypothesis if the sample sizes for individual treatment groups are the same. Thus, the adjusted weights for the Dunnet test should be somewhere between the adjusted weights of the Sidak test and the regular weights of no adjustment. A relatively simpler approach without the need of numerical computation may be to use the mean or geometric mean of the adjusted weights of the Sidak test (see (8)) and no adjustment.

Regardless of the way of specifying the weights, as long as they are pre-specified at the design stage or before any data unblinding and satisfy the constrain of , the type I error rate should be appropriately controlled. Note that if a sample size increase adaptation is performed for stage 2, the adjusted weight discussed above for the test statistic of stage 1 may still not be small enough to balance the weights across patients.

Initial sample size and power consideration

For the seamless design, we need to determine the appropriate initial sample sizes for the interim analysis and the whole study so that we can have reasonable probability to make the right treatment selection or to avoid the false no-go decision at the interim analysis as well as have potentially enough power for the final analysis. The final sample size for study may depend on the interim results in case they deviate from the assumptions made at the design stage. Clearly, the sample size calculation depends on the objective of the trial and the corresponding analysis approach. Suppose we would like to select one among the I dose for stage 2 with potential early trial stopping for either futility or efficacy. The non-binding futility criterion is that the observed treatment effects for all doses are smaller than a threshold Δ and the significance level for early efficacy claim is α₁. Then the probability of meeting the futility criterion for all doses at the IA is

If this probability is not small given the assumed clinically meaningful treatment effects , the sample sizes for the interim analysis may not be large enough and we need to adjust the sample sizes to reduce the chance of a false no-go decision.

If only the dose with the largest observed treatment effect (or smallest p-value) will be evaluated for early efficacy claim, the multiplicity adjusted p-value p^A ₍₁₎₁ (based on a pre-specified test) for the dose should be less α₁. The probability for making the early efficacy claim is given by

If (10) is very small even for reasonable sample sizes n_i1’s, we may set α₁ to be very small so that we can reserve more alpha for the final analysis. Different sets of may be used for (9) and (10). Method for deriving the critical value or significance level α₂ for the final analysis has been discussed in Section 2. The overall power is then

The initial sample sizes for the two stages thus can be calculated probably through simulation for the desired overall power given the assumed trial parameters.

Adaptive design

Results from the unblinded interim analysis may not be consistent with the assumptions made at the design stage. Conditional power for the treatment effect to be significant at the final analysis is calculated based on the originally assumed and the updated treatment effects for the data of stage 2. If the conditional power is too small, we may stop the trial for futility. If it is large enough, we will continue the trial according to the originally planned sample size. Otherwise, we will perform sample size adaptation for the desired conditional power for the final analysis. The conditional power with the pre-specified adjusted weights can be calculated as

where Z follows a standard normal distribution and δ₍₁₎ can be or other values. For (11) to be 1-β,

The sample size per group for stage 2 and a balanced design is

If this sample size is too large, we may stop the trial early at stage 1 or keep the originally planned sample size for stage 2.

Calculations and simulations

In this section, we use simulations to compare various adjustments to the combination test’s weights and investigate their impact to the power of the test. For simplicity, we assume only the first standardized treatment effect is not null (δ₍₁₎=0.2), and all the remaining arms are null . Only one active treatment from stage 1 is selected for stage 2 based on the maximum treatment effect estimate or the smallest p-value (the I=1 case is used as a benchmark for the weight/power since neither multiplicity adjustment nor treatment selection is needed). Sample sizes for the final analysis, n₁+n₂, are selected to obtain 80%, 90% and 95% target power for comparing one active treatment to the control with a fixed design without interim analysis and multiplicity adjustment for the test statistic of stage 1. Thus, the corresponding power with the multiplicity adjustment should be less than the target level.

The interim analysis is assumed to be performed with information fractions or . Based on these configurations for the design parameters, the weights can be calculated as in Section 2 and are shown in Figure 1.The regular weight under each simulation design scenario is , which depends on only the information fraction for the interim analysis and is fixed regardless of the number of arms for stage 1 and target power. The adjusted weights use here for the Dunnett test are the same as those of the Hommel test. They are actually the mean and geometric mean of the Bonferroni adjusted weight and the regular weight. The more conservative the multiplicity approach is, the larger the weight adjustment; the Bonferroni approach has the largest adjustment compared to the other approaches while the Dunnett (Hommel) mean approach has a relatively smaller adjustment in all scenarios. For all approaches, large adjustments are observed when the number of arms for stage 1 is larger, the target power is smaller, or the information fraction for the interim analysis is smaller.

(Figure 2) presents simulation results for power of combination test for the selected treatment using different methods. For each combination of target power, information fraction, and the number of active arms, the number of simulation repetition is 10000 which is enough for power evaluation. With multiplicity adjustment, power decreases with the number of arms of stage 1. Even though the unadjusted weight and adjusted weights (Figure 1) can be very different, the differences in power are relatively small which implies that power is not very sensitive to the weight unless in an extreme case with very large weight for stage 1. With or without the adjustment in combination weights, the Dunnett approach has relatively larger power compared to the Sidak and Bonferroni approaches. The two adjusted weights (using arithmetic or geometric mean of the Sidak adjusted weight and the regular weight) for the Dunnett approach are basically identical so the corresponding lines in each panel are overlapping. Adjusted weight associates with slightly larger power particularly for the Sidak approach. For Bonferroni approach, when the information fraction is small and the number of active arms is large, even though the adjustment brings down the weight assigned to the first stage, the power is slightly lower. The reason for this could be because that the weight for stage 1 is over adjusted and passed the “optimized” weight where the power of the combination test for selected treatment will peak (Figure S.1). In practice, however, this should rarely happen since we usually will only have up to 5 active treatments/dose to be compared with a common control.

Discussion

A weighted combination test is often applied to combine test statistics of two stages for a two-stage design. When a treatment selection (e.g., to select one dose from multiple doses) is performed based on the interim results, multiplicity adjustment should be performed for the test statistic of the first stage. The commonly used weights are the square roots of the proportions of the pre-planned sample sizes of the two stages ignoring the multiplicity adjustment. In this research, we consider adjusted weights for different multiplicity adjustment methods for the weighted combination test to evaluate whether the adjustment can increase power.

Simulation results demonstrate that power is actually not sensitive to the weights unless they are in very extreme domain. Thus, it is not critical to perform weight adjustment in terms of power improvement. However, in the spirit of one patient one vote or equal contribution for each patient (measured by each patients’ weight in analysis), the weight adjustment makes sense.

Multiplicity adjustment on p-value only controls the overall type I error rate of making false claims. To quantify the magnitude of treatment effects, we need the estimate of the treatment effects. Several authors have discussed various adjustments for obtaining the mean unbiased, medium unbiased and bias reduced estimators with treatment selection at the interim analysis [4,14].

References

1. Robertson DS, Choodari Oskooei B, Dimairo M, Flight L, Pallmann P, et al. (2023) Point estimation for adaptive trial design I: a methodological review. Statistics in Medicine 42: 122-145.
2. Robertson DS, Choodari-Oskooei B, Dimairo M, Flight L, Pallmann P, et al. (2023) Point estimation for adaptive trial design II: a methodological review. Statistics in Medicine 42: 2496-2520.
3. European Medical Agency (2017) Guideline on multiplicity issues in clinical trials.
4. Bretz F, Koenig F, Brannath W, Glimm E, Posch M (2009) Adaptive designs for confirmatory clinical trials. Statistics in Medicine 28: 1181-1217.
5. Dunnett CW (1955) A multiple comparison procedure for comparing several treatments with a control. Journal of American Statistical Association 50: 1096-1121.
6. Hommel G (1988) A stagewise rejective multiple test procedure based on a modified Bonferroni test. Biometrika 75: 383-386.
7. Simes RJ (1986) An improved Bonferroni procedure for multiple tests of significance. Biometrika 73: 751-754.
8. Šidák ZK (1967) Rectangular Confidence Regions for the Means of Multivariate Normal Distributions. Journal of the American Statistical Association 62(318): 626-633.
9. Marcus R, Peritz E, Gabriel FR (1976) On closed testing procedure with special reference to ordered analysis of variance. Biometrika 63: 655-660.
10. Bauer P (1989) Multistage testing with adaptive designs (with discussion). Biometrie und Informatik in Medizin und Biologie 20: 130-148.
11. Bauer P and Kohne K (1994) Evaluation of experiments with adaptive interim analysis. Biometrics 50: 1029-1041.
12. Cui L, Hung HMJ and Wang SJ (1999) Modification of sample size in group sequential clinical trials. Biometrics 55: 853-857.
13. Hochberg Y and Tamhane AC (1987) Multiple Comparison Procedures. John Wiley & Sons, Inc.
14. Brannath W, Koenig F, Bauer P (2006) Estimation in flexible two stage designs. Statistics in Medicine 25: 3366-3381.