Normality Assessment of Several Quantitative Data Transformation Procedures
Dago Dougba Noel1*, Kablan Gnoan Aka Justin1, Alui Konan Alphonse2, Lallié Hermann Désiré1, Dagnogo Dramane1, Diarrassouba Nafan1 and Giovanni Malerba3
1Department of Biochemistry and Genetic, Peleforo Gon Coulibaly University BP 1328 Korhogo, Cote d’Ivoire
2Department of Geosciences, Peleforo Gon Coulibaly University BP 1328 Korhogo, Cote d’Ivoire
3Department of Neurological, University of Verona, Italy
Submission: August 17, 2020;Published: February 02, 2021
*Corresponding author: Dago Dougba Noel, Department of Biochemistry and Genetic, UFR Biological Sciences, Peleforo Gon Coulibaly University BP 1328 Korhogo, Cote d’Ivoire
How to cite this article: Dago D N, Kablan G A J, Alui Konan A, Lallié Hermann D, Dagnogo D, et al. Normality Assessment of Several Quantitative Data Transformation Procedures. Biostat Biom Open Access J. 2021; 10(3): 555786.DOI:10.19080/BBOAJ.2021.10.555786
Abstract
Usually, quantitative data standardization and/or normalization procedures requested in biological and as well in biomedical data analysis with the purpose to infer about linear regression relationship between processed variables and/or conditions. Here, we embarked to understand performance of quantitative data transformation systems in terms of reducing data variability as well as assessing data distribution normality by a computational statistic approach. For this purpose, we performed several multivariate descriptive and analytical statistical tests. Even if results shown drastic reduction of data variability by applying presently data transformation procedures, it is noteworthy to underline the relative opposite attitude of Exponential (Expo) data standardization system in that sense. In addition although, results revealed variance homogeneity for data processed by both Maximum and Logarithm data transformation methods, it is noteworthy to underline a relative variance homogeneity with regard data submitted to Box-Cox, Z-score, Minimum-Maximum and Square Root data transformation methods. Further, findings exhibited high aptitude of Square Root, Box-Cox and Logarithm quantitative data standardization methods, in stabilizing processed data variability. Interestingly, results shown high performances of Logarithm and Box-Cox data standardization systems in term of adjusting data normal distribution. In addition, multiple comparison of mean by Turkey contrast test suggested the high performance in term of data normality with regard Box-Cox standardization method. In conclusion, even if our results revealed heterogenic performances of presently processed quantitative data transformation methods, it is noteworthy to underline the high performances of both Box-Cox and Logarithm methods, in adjusting and reducing data normality and variability respectively, allowing improving data aptitude for subjacent linear regression analysis.
Keywords: Quantitative data transformation; Data normality; Data variability; Computational statistical analysis
Abbreviations: Min-Max: Minimum-Maximum; Bcox: Box-Cox; Expo: Exponential; Log: Logarithm; Sqr: Square Root; PCA: Principal Component Analysis; Pv: probability value: RC1: Rotate Components 1
Introduction
Data standardization represents a challenge in biological and as well in biomedical statistical data analysis. It is commonplace in biostatical survey to check for a general linearity model and/or linear model between analyzed and/or processed parameters. Indeed, statistical standardization systems allow reducing variability heterogeneity among processed statistical variables and represent a powerful tool in realizing linearity link between those variables. However, statistical errors are common in several biological as well as biomedical surveys. It reported that about 50% of the published articles have at least one error [1,2]. Usually, parametric test statistical analysis comprising t test, correlation, regression, analysis of variance, are based on the assumption that processed data follows a normal distribution, suggesting that the populations from which the samples are taken are normally distributed [3-6]. For this purpose, authors apply several quantitative data standardization procedures aiming to adjust data normality.
We believe that indiscriminate used of data standardization systems could represent a source of statistical error in numerous bio-statistical and/or biomedical studies. Several quantitative data transformation systems and/or methods are available in scientific literature. In addition, normality assumptions are critical for many univariate interval and hypothesis tests. Therefore, in parametric test statistical survey, it is important to test the normality assumption. The Box-Cox (Bcox) normality plot can often be used to find a transformation that will approximately normalize the data [7,8]. The log-transformation is widely used in biomedical and psychosocial research to deal with skewed data [9]. Another popular use of the log transformation is to reduce the variability of data, especially in data sets that include outlying observations. Again, contrary to this popular belief, log transformation can often increase not reduce the variability of data whether or not there are outliers [8,9]. Normalization is used to scale the data of an attribute so that it falls in a smaller range, such as 1.0 to 1.0 or 0.0 to 1.0. It is generally useful for classification algorithms. Normalization is generally required when we are dealing with attributes on a different scale [9,10]; otherwise, it may lead to a dilution in effectiveness of an important equally important attribute because of other attribute having values on larger scale. Concerns with regard statistical parameters and/or variables attributes on a different scale is recurrent in agronomic as well as in quantitative genetic data processing survey [11-13]. When multiple attributes are there but attributes have values on different scales, this may lead to poor data models while performing data mining operations.
In statistics, normalization refers to the creation of shifted and scaled versions of statistics, where the intention is that these normalized values allow the comparison of corresponding normalized values for different datasets (heterogenic data) in a way that eliminates the effects of certain gross influences, as in an anomaly time series [14,15]. Therefore, heterogenic data transformation procedure, bring all the attributes on the same scale. Indeed, among those quantitative data normalization methods, decimal scaling method normalizes by moving the decimal point of values of the data. To normalize the data by this technique, we divide each value of the data by the maximum absolute of data. In minimum-maximum (Min-Max) data normalization technique, linear transformation is performed on the original data, while in z-score data normalization procedure, values are normalized basing on mean and standard deviation parameters. Basing on these evidences, quantitative data standardization as well as normalization procedures can exhibit divergent properties and aptitudes in terms of parametric distribution such as normal distribution and as well data variability reduction. Here we embarked in comparing several quantitative data standardization and/or normalization and/or transformation procedures on the same quantitative data set with the purpose to assess those processed data normality as well as standardization and/or distribution performances. For this purpose, we performed a computational statistical survey by applying multivariate and analytical statistical analysis.
Material and Methods
Quantitative data used for the present study were drawn from previous experiments as described by Diarassouba et al. 12 and Dago et al.16. Briefly, collected data included four (4) growth parameters (diameter, plant height, leaf length and leaf number) of two maize varieties, treated by both rhizobacteria and foliar bio-fertilizing [12,13]. Further, collected data for each treatment were summarized in a matrix including four columns describing variables parameters (two maize varieties growth parameters) and ninety-six rows corresponding to the observation number [12,16]. Next, we submitted the above-mentioned data matrix to Box-Cox, Logarithm, Square Root, Inverse and Z-score, Minimum, Exponential and Minimum-Maximum quantitative data standardization as well as normalization (data transformation) procedures.
Quantitative data transformation methods
We focused on eight (8) quantitative data transformation systems in the present comparative study. Processed quantitative data standardization and/or normalization procedures are as following Box-Cox (Bcox), Exponential (Expo), Inverse, Logarithmic normalization, Maximum, Minimum-Maximum, Square Root and Z-score. Above-mentioned data transformation systems was applied to the same data matrix (collected data) generating a new data set for each standardization and/or normalization methods.
Box-Cox transformation
A Box Cox transformation is a way to transform non-normal dependent variables into a normal shape. Normality is an important assumption for many statistical techniques; if your data isn’t normal, applying a Box-Cox means that you are able to run a broader number of tests. Box and Cox [17] take the idea of having a range of power transformations rather than the classic square root, log, and inverse, available to improve the efficacy of normalizing and variance equalizing for both positively- and negatively-skewed variables [18]. The transformation of iy′ has the form:
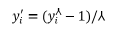
Exponential (Expo) data transformation
An exponential transformation provides a useful alternative to Box and Cox’s one parameter power transformation and has the advantage of allowing negative data values [19].
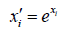
Inverse transformation
This normalization makes very small numbers very large and very large numbers very small. This transformation has the effect of reversing the order of your scores [18].
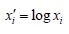
Logarithmic (Log) transformation
Log-normal variables seem to be more common when outcomes are influenced by many independent factors [18]. The Log-normal transformation formula is as following:
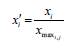
Maximum (Max) normalization
This normalization system give a new range of data between 0 and 1. Maximum normalization process belongs to centered and reduced transformation family. The particularity of this process is that the transformed data is always superior to 0 and can be equal to 1. So, 0˂Xnormalized≤1. Maximum normalization formula is as following:
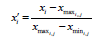
Minimum-Maximum normalization
This normalization also consists in centering and reducing the data of each variable column in the interval [0-1] [10]. Min-Max normalization is the technique that keeps relationship among original data and provides linear transformation on original range of data. Mathematical formula with regard above mentioned normalization system is as following:
Square root normalization
The square root transformation is the technique that stabilizes variance and allows a normal distribution of data. The mathematical formula of that quantitative data transformation is:
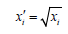
Z-score normalization
In z-score normalization, the values xi for an attribute A is normalized basing on the mean and standard deviation of A [20]. Indeed, Z scores, or standard scores, indicate how many standard deviations an observation is above or below the mean. These scores are a useful way of putting data from different sources onto the same scale. A value xi of A is normalized to xi’ by computing:
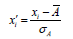
A and σA are the mean and the standard deviation respectively of attribute A.
Computational statistical analysis
We performed a comparative analysis of above mentioned quantitative data standardization procedures by using several function of R package (R Core Team, 2020) software. Hence, we used empirical cumulative distribution function (ecdf) in assessing normalized data distribution. In the same tendency, we performed a multivariate boxplot analysis by assessing normalized data distribution around median parameter.
It is noteworthy to underline that presently processed computational statistical analysis partially based in our previous developed pipeline [16]. Indeed, above-mentioned pipeline includes R package pvclust which uses bootstrap resampling techniques to compute p-value for each hierarchical clusters [21-23]. Hence, we checked for compute p-value clustering performance with regard analyzed quantitative data standardization procedures. Next, we achieved an Anova test with the purpose to assess above mentioned quantitative data normalization systems variability. Pipeline also includes FactoMineR package principal component analysis graph by assessing processed quantitative data transformation (variables) relationship in measuring observed data (factors) distribution and/or distribution.
We evaluated normalized data distribution normality by applying ShapiroWilk normality test [24,25]. Indeed, it is possible to use a significance test comparing the sample distribution to a normal one in order to ascertain whether data show a serious deviation from normality or not. Shapiro-Wilk’s method is widely recommended for normality test [25]. In Shapiro-Wilk’s method, the null hypothesis is that sample distribution is normal. If the test is significant, the distribution is non-normal. From the output, the p-value > 0.05 implying that distribution of the data are not significantly different from normal distribution. In other words, we can assume the normality. In addition, we tested density plot checking for response variable closed to normality. Next, we assessed variance homogeneity of data under analyzed data transformation procedures by Bartlett test (Bartlett test of homogeneity of variances). Further, we executed various correlation tests (Pearson correlation test) as well as principal component analysis with the purpose to evaluate the degree of similarity and/or dissimilarity between quantitative data transformation methods. Further, we performed a quantile-quantile plot statistical descriptive analysis in assessing transformed data normal distribution by R qqnorm and qqline functions [26].
Results
Multivariate statistical analysis evaluating data distribution and distribution function of quantitative data normalization systems We assessed normalized data distribution by performing a multivariate descriptive statistical analysis. Empirical cumulative distribution function in assessing normalized data distribution, shown an apparent similarity between Z-score, Minimum-Maximum (Min.Max) and Maximum (Max), Logarithm (Log), Square Root (Sqr) and Box-Cox quantitative data transformation systems (Figure 1). However, empirical cumulative distribution graph concerning above-mentioned quantitative data transformation methodologies, exhibited heterogenic data distribution compared to median parameter. Data distribution referring to median parameter by a boxplot multivariate descriptive statistical analysis confirmed this tendency (Figure 1). In addition, both empirical cumulative distribution function graphic and boxplot multivariate descriptive statistical analysis, shown a strong difference between Inverse and Exponential quantitative data normalization systems, as well as between the latter’s and Z-score, Minimum-Maximum and Maximum, Square Root and Box-Cox and Logarithm data normalization and/or standardization methods. Boxplot multivariate statistical analysis, assessing data normal distribution around median position parameter, suggested similar behaviors between Logarithm and Box-Cox data standardization methods (Figure 1). The same analysis suggested similar data normality performance with regard Z-score, Minimum-Maximum and Maximum and Square Root data transformation systems. As a whole, the present survey although displaying relative heterogenic aptitudes with regard processed quantitative data normalization as well as standardization methods, exhibited some similitude among most of them in terms of normalized data distribution and/or dispersion.
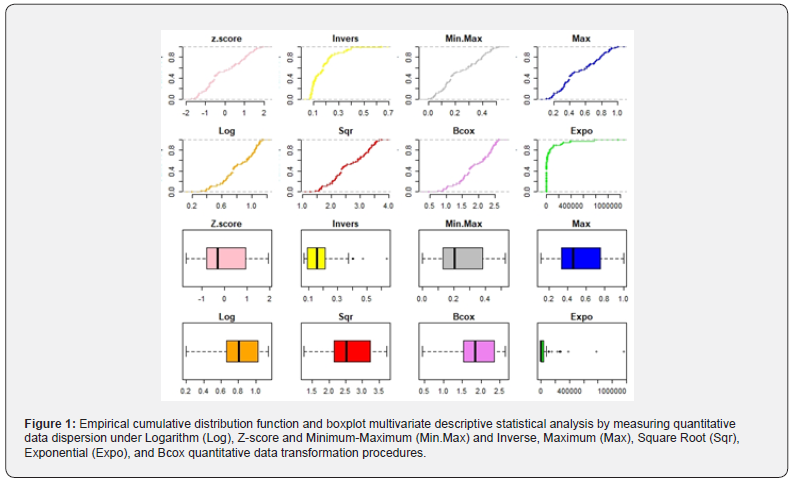
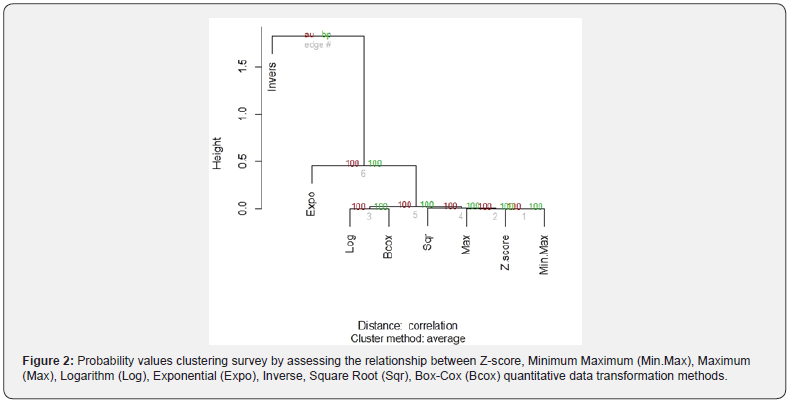
Performance assessment of quantitative data transformations methodologies by probability value (Pv) clustering analysis Here, we focused on bootstrap resampling technique comparing p-values parameters for hierarchical clustering survey between processed quantitative data normalization and/or standardization methods. The present hierarchical clustering analysis revealed highest probability value (AU and BP p-values = 100) between all processed quantitative data transformation methods (Figure 2). Apparently, that probability clustering analysis suggested an equal performance as well as aptitude with regard Minimum-Maximum, Z-score and Maximum, Square Root, Box-Cox and Logarithm (Log) transformation methods as opposite to Inverse and Exponential quantitative data transformation systems (Figure 2). Hierarchical clustering analysis exhibited an equal performance between Minimum-Maximum, Z-score and Maximum, Square Root, Box-Cox and Logarithm quantitative data transformation methods. The same analysis revealed high concordance between
(i)Z-score and Minimum-Maximum,
(ii)Z-score and Maximum,
(iii)Box-Cox and Logarithm,
(iv)Maximum and Square Root and
(v)Square Root and Box-Cox data transformation methodologies respectively (Figure 2, Supplementary Figure 1A and B).
In addition, probability value hierarchical analysis, as expected, revealed an inverse attitude of Inverse quantitative data normalization methodology, vis-à-vis of the others processed data quantitative transformation systems (Figure 2, Supplementary Figure 1C). Although, the present hierarchical clustering analysis shown high AU and BP probability values, by comparing all processed data standardization and/or normalization methodologies, it is noteworthy to underline the low clustering concordance between
(i)Exponential data transformation methodology and
(ii)Logarithm, Z-score, Box-Cox and Square Root, Maximum and Minimum-Maximum quantitative data transformation procedures (Figure 2, Supplementary Figure 1C and D).

Relationship between factor and variable evaluating quantitative data transformation performances
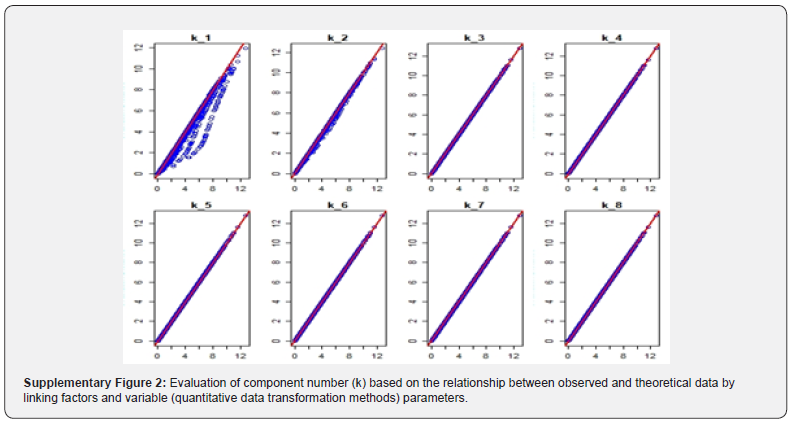
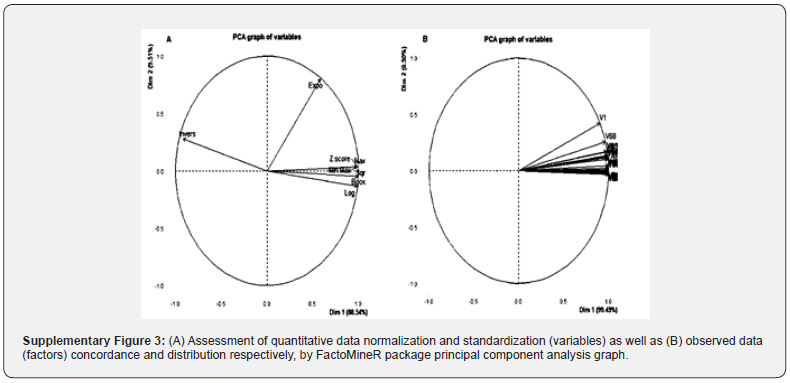
We performed a biplot Principal Component Analysis (PCA) with the purpose to link factors (transformed data distribution) and variables (quantitative data transformation methodologies) by two component. Indeed, our analysis suggested two axes as enough in assessing processed data distribution and/or variability (Supplementary Figure 2). In supplementary Figure 2, dots begin to be roughly aligned along a straight line for k=two (2), suggesting the distances in the PCA environment are well proportional to the real observed distances guarantying a correct interpretation with regard analysis results. Basing on this evidence, the present analysis confirmed the good relationship and/or association between Maximum (Max), Minimum-Maximum (Min-Max) and Square Root (Sqr), Z-Score, Logarithm (Log) and Box-Cox quantitative data transformation methods by it Component 1. In addition, as expected, Component 1 revealed a negative correlation between Invers data transformation procedure and the other quantitative data transformation methodologies. Projection on Component 1, shown a weak correlation between
(i)Exponential (Expo) and
(ii)Inverse, Maximum, Minimum-Maximum and Square Root, Z-Score, Logarithm and Box-Cox quantitative data transformation methods (Figure 3B; Supplementary Figure 1B).
Component 1 also revealed a relative reduction of data variability by processing all analyzed data transformation procedures as opposite to Component 2 (Figure 3A and Supplementary Figure 3). Therefore, merging observed data (factors) variability by Component 2 with those of quantitative data transformation systems (variables) by Component 1, findings suspected Exponential (Expo) quantitative data transformation procedure as a potential source of data variability (Supplementary Figure 1C and D and Supplementary Figure 3). In addition, scatter plot tridimensional analysis discriminated five (5) groups processing transformed data population (Figure 3C). Interestingly, although Exponential data transformation exhibited feeble performance with the purpose to reduce data variability, the present analysis confirmed high performance of presently processed data transformation methodologies in dropping transformed data variability (Figure 3A and C).
Assessment of quantitative data transformation methods normality by Shapiro-Wilk normality test
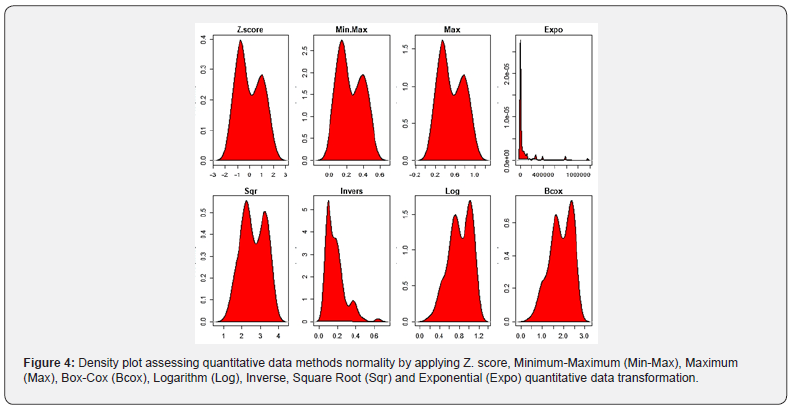
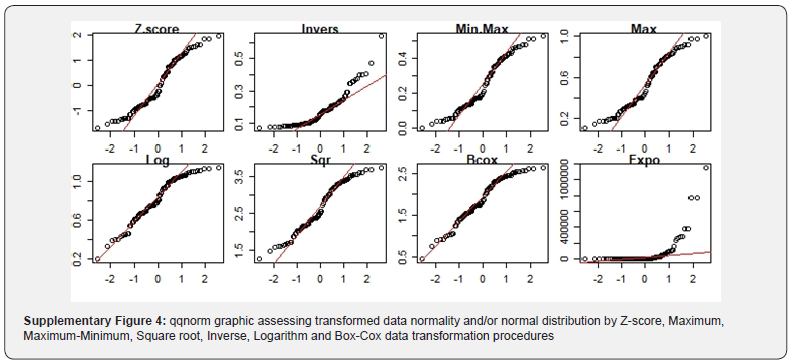
Here we processed a Shapiro-Wilk normality test by showing a strong difference between processed quantitative data standardization as well as normalization systems. Indeed, Shapiro probability test exhibited weak probability (Pv) value for Exponential (9.57e-18<<<0.05) and Inverse (5.75e-09<<0.05) data transformation methodologies respectively. This result suggested a low performance of these two data standardization and/or normalization systems in normalizing quantitative data. Interestingly, the other quantitative data transformation methods displayed an opposite attitude by exhibiting Shapiro probability tests and/or probability values relatively inferior to 0.05 (probability values range from 0.0001 to 0.0005). Among these quantitative data transformation procedures, Logarithm (Log) and Box-Cox methods exhibited probability coefficient relatively near to 0.05 (ratio = 0.0005/0.05= 0.01) by contrast to Z-score, Maximum (Max) and Minimum-Maximum (Max-Min) (ratio = 0.0002/0.05 = 0.004) and Square Root (Sqr) (ratio =0.0001/0.05 = 0.002) methods (Table 1). Density plot assessing data normality shown a similar performance between Z-score, Minimum-Maximum and Maximum data transformation methodologies (Figure 4). The same analysis exhibited and as well confirmed the opposite skill of both Inverse and Exponential data transformation, in term of normalizing data. By contrast, density plot analysis clearly shown high performance of Logarithm and Box-Cox quantitative data transformation methodologies in adjusting data normality (ratio =0.01/0.004 = 2.5 fold and 0.01/0.002 = 5.0 fold respectively), with respect to the others considered quantitative data transformation systems (Figure 2 and Table 1). In addition, basing on Shapiro probability test, we suspected Z-score, Minimum-Maximum and Maximum as intermediary quantitative data transformation methods between?
(i)Square Root (Sqr) and both
(ii)Logarithm and Box-Cox data transformation methods (Table 1 and Supplementary Figure 4).


Bartlett test measuring variance homogeneity between quantitative data transformation procedures We assessed quantitative data transformation methods variances homogeneity by Bartlett test of homogeneity of variance. Findings revealed weak Bartlett’s S-squared coefficient (Bartlett’s S-squared = 0.53) and high p value (p = 0.468) by comparing Maximum (Max) and Logarithm (Log) transformation method, by contrast to the other Bartlett comparative test between transformation methods (Table 2). In the other words, findings shown variance homogeneity for data processed by both Max and Log quantitative data transformation methodologies. However, present results displayed relative weak Bartlett’s coefficient and relative high p values for the following Bartlett comparative analysis:
(i)Squared Root (Sqr) Vs. Box-Cox,
(ii)Minimum-Maximum (Min.Max) Vs. Inverse,
(iii)Z.score Vs. Square Root and
(iv)Minimum-Maximum Vs. Logarithm and
(v)Minimum-Maximum Vs. Maximum respectively (Table 2).

In addition, results shown a contrast between Exponential (Expo) data transformation methodology and the other processed data transformation analysis, in terms of measuring variance homogeneity. Indeed, comparison between Exponential data transformation method and the other processed data transformation methods, exhibited high Bartlett’s K-square coefficient (Bartlett’s S-squared ≥ 2149.8) associated to very low p value (p < 2.2e-16). Several clustering analysis based on Pearson correlation, Z-score and as well, principal component clustering analysis confirmed the divergence aptitude and/or behavior of Exponential quantitative data transformation method, in terms of stabilizing transformed data variance (Supplementary Figure 1).
Results of Horn’s parallel analysis for factor retention by using the mean estimate
We processed 5000 iterations using the mean estimate with the purpose for factor retention. Findings suggested two factors retention (adjusted eigenvalues > 0 indicate dimensions to retain) in explaining data variability (Table 3). Parallel principal component analysis confirmed that result by comparing adjusted and unadjusted eigenvalue as well as retained and/or un-retained and random Eigenvalues (Figure 3). Next, we focused on inference statistical analysis by setting two factor as enough to explain processed data variability. For this analysis, we analyzed a variant matrix by estimating communality (h2) and specific (u2) variances explained by each of the two axes and/or components and/or factors (Table 4). Rotate components 1 (RC1) and 2 (RC2) exhibited an opposite behaviors in explaining the variances (communality and specific variance) on the one hand of
(i)Z-score, Minimum-Maximum (Min-Max) and Maximum (Max), Square Root (Sqr), Logarithm (Log) and Box-Cox data transformation methods, and on the other hand
(ii)of Inverse and Exponential (Expo) data transformation procedures. The same analysis shown weak specific variance associate to Box-Cox, Logarithm and Square Root quantitative data transformation systems respectively (Table 4).

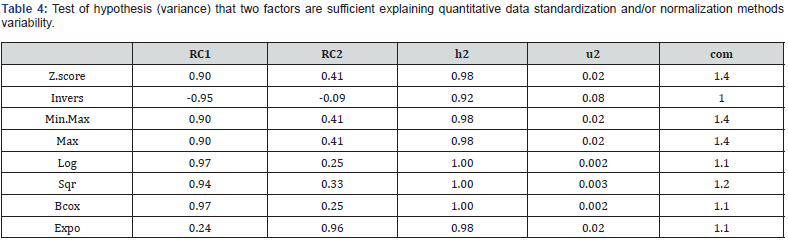
Inverse data transformation methodology exhibited a relative high specific variance as opposite to the others analyzed quantitative data transformation systems. Also, inference statistic test of the hypothesis that two components are sufficient basing on mean item complexity = 1.2 (Table 2), exhibited the following results:
(i)root mean square of the residuals (RMSR) = 0.02 and
(ii)with empirical chi square 1.51 associated to p < 1. In the other words, all processed data transformation systems seem to exhibit acceptable performances in reducing significantly processed quantitative data variability (Table 3).
Link between processed data transformation methodologies by general hypothesis and multiple comparison for parametric model
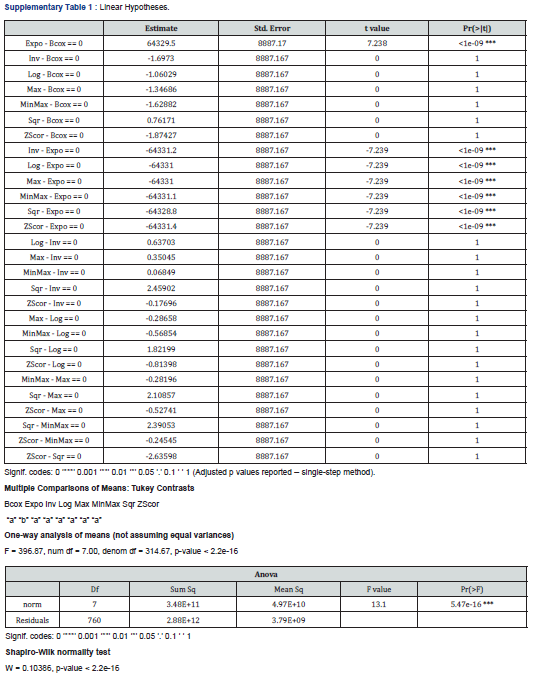
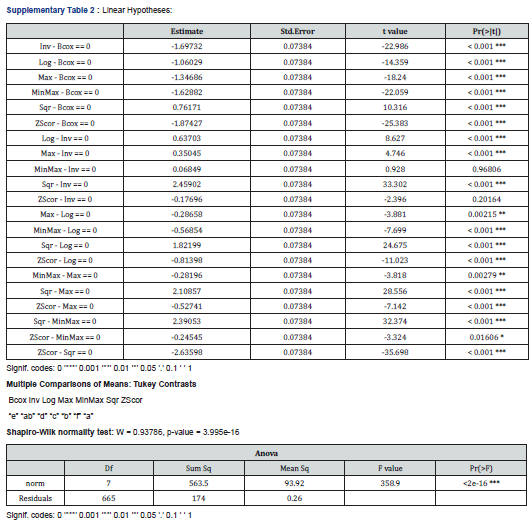
Focusing on general hypothesis and mean multiple comparison between processed quantitative data transformation, Turkey contrast survey confirmed difference between exponential (Expo) and the others analyzed quantitative data transformation methodologies in term of data normality and as well variance stabilization. Indeed, exponential (Expo) data transformation methodology, strongly influences Z-score, Maximum (Max), Minimum-Maximum (Min-Max), Square Root (Sqr), Logarithm (Log), Box-Cox and Inverse quantitative data transformation methods (Figure 6A). Apparently, the same analysis by processing mean multiple comparison based on Turkey contrast analysis, suggested no significant difference between Z-score, Maximum (Max), Minimum-Maximum (Min-Max), Square Root (Sqr), Logarithm (Log), Box-Cox and Inverse data transformation systems (Supplementary table 1). Next, we excluded Exponential data transformation method aiming to reduce bias in previously evoked Turkey test by comparing Z-score, Maximum (Max), Minimum-Maximum (Min-Max), Square Root (Sqr), Logarithm (Log), Box-Cox and Inverse data transformation methodologies (Figure 6B). This analysis, relatively exhibited a significant difference between processed quantitative data transformation systems (Supplementary Table 2). The same survey suggested a relative high performance of Box-Cox and Logarithm quantitative data transformation systems respectively in comparison to Inverse, Maximum, and Minimum-Maximum, Logarithm and Z-score data transformation methods (Figure 6B).
Discussion
In this article, we focused on a comparative study between eight (8) quantitative data standardization and normalization procedures by assessing their impact on data distribution as well as normality performances. Findings by performed empirical cumulative distribution function and as well, boxplot multivariate descriptive statistical analysis by measuring quantitative data dispersion suggested opposite attitude of Inverse and Exponential quantitative data transformation methods with respect to the others analyzed data transformation methodologies. Indeed, Horn’s parallel analysis revealed by it rotate components 1 (RC1) and 2 (RC2), an opposite behaviors in explaining communality and specific variance on the one hand of
(i)Z-score, Minimum-Maximum (Min-Max) and Maximum (Max), Square Root (Sqr), Logarithm (Log) and Box-Cox data transformation methods, and on the other hand
(ii)of Inverse and Exponential (Expo) data transformation procedures.
The same analysis shown weak specific variance associate to Box-Cox, Logarithm and Square Root quantitative data transformation systems respectively as opposite to Inverse data transformation procedure. Probability clustering analysis based on average cluster method as well as correlation distance relatively confirmed the same tendency. Although this analysis suggested a good performance with regard all processed data transformation methodologies in term of reducing data variability, it revealed high agreement between Minimum-Maximum, Maximum and Z-score quantitative data transformation methods as well as between Box-Cox and Logarithm quantitative data transformation systems.
As previously reported, Horn’s parallel analysis exhibited feeble specific variance associate to Box-Cox, Logarithm and Square Root quantitative data transformation systems. Indeed, transformations that stabilize the variance of error terms (i.e. those that address heteroscedaticity) often also help make the error terms approximately normal [27,28]. Basing on this evidence, Box-Cox, Logarithm and as well Square Root quantitative data transformation methods should help making the error term normal as opposite to Inverse and Exponential data transformation methods, and relatively to Minimum-Maximum, Maximum and Z-score quantitative data scaling methods. Interestingly, Bartlett test measuring variance homogeneity between quantitative heterogenic data under presently processed data transformation methods suggested high performance in term of variance homogeneity between Logarithm and Maximum and as well between Box-Cox and Square Root data transformation methods. The same survey displayed non-significant performance with regard Exponential quantitative data transformation method, vis-à-vis of above-mentioned variance homogeneity test. The purpose of quantitative data transformation consist in making data relatively suitable for modeling with linear regression if the original data violates one or more assumptions of linear regression [29].
Another assumption of linear regression is homoscedasticity, that is the variance of errors must be the same regardless of the values of predictors. If this assumption is not verified, making data heteroscedastic, data transformation is needed, triggering homoscedasticity assumption allowing easily linking processed variables in a linear regression model [27]. An application of data transformation is to address the problem of lack of normality in error terms. The normal distribution is widely used in basic and clinical research as well as biomedical studies to model continuous outcomes. Unfortunately, the symmetric bell-shaped distribution often does not sufficiently describe the observed data. Quite often data arising in real studies are so skewed that standard statistical analyses of these data yield invalid results. Many methods have been developed to test the normality assumption of observed data [25]. When the distribution of the continuous data is non-normal, transformations of data are applied to make the data as normal as possible and thus, increase the validity of the associated statistical analyses.
The assumption of normality is especially critical when constructing reference intervals for variables [30]. Normality and other assumptions should be taken seriously, for when these assumptions do not hold, it is impossible to draw accurate and reliable conclusions about reality [31,6]. Shapiro Wilk test (Patrick, 1995) conferred high data normality aptitude to Logarithm and Box-Cox standardization methods and relatively to Maximum-Minimum, Maximum, Z-score and Square root [25]. The logarithm transformation is, arguably, the most popular among the different types of transformations used to transform skewed data approximately conform to normality [8]. However, using transformations in general and logarithm transformation in particular can be quite problematic. If such an approach is used, the researcher must be mindful about its limitations, particularly when interpreting the relevance of the analysis of transformed data for the hypothesis of interest about the original data. Several studies suggested overcoming with regard appropriate statistical distribution to observed data by applying generalized estimating equations rather than using classical data transformation methods (i.e. log transformation) [32,33].
Generalized estimating equations waives the distribution assumption and offer valid inference regardless of the distribution of processed data. However, this is only suitable for skewed data and as well for data adjusted by a parametric distribution (i.e. normal distribution). Data transformation is a proven method in statistical modeling and often used to linearize the relationships between dependent and independent variables, with the purpose to homogenize the variance of residuals and to normalize regression residuals. A failure in variance error homoscedasticity and as well in normalizing regression residuals will not cause bias in the model estimates but will reduce the reliability of significance tests as well as the estimation of confidence intervals of the regression coefficients. In addition, our findings by processing general hypothesis and mean multiple comparison with regard standardization systems by Turkey test revealed a relative high performance of Box-Cox data transformation methods as opposite to logarithm, Z-score, Maximum, Maximum-Minimum and Square Root quantitative data standardization systems. Indeed, comparing the Logarithmic transformation and the Box-Cox transformation for individual tree basal area increment models, Fischer [34] shown the high performance of Box-Cox data transformation method. In fact, in this study Box-Cox transformation yielded a better residual structure of the models by reducing the skew.
The same survey displayed smaller bias transformation by using the Box-Cox transformation as opposite to logarithm transformation. The same study revealed that the mean squared error of estimation is smaller with the Box-Cox transformation; and as well, the Box-Cox transformation leads to systematically higher estimated values than Logarithmic transformation. Hence, the Box-Cox transformation should be considered as a viable alternative in statistical modeling if the transformation of variables is required [34]. Low aptitude with regard Exponential and Inverse data transformation in reducing data variability as well as in adjusting data normality could be due to processed positive value of analyzed data [16,12]. Indeed, our analysis suspected Exponential data transformation as a potential source of transformed data variability. We believe that the used of positive quantitative data exclusively (maize and soybean growth parameters) in the present study, could constitute a limit to performed computational statistical analysis in evaluating adequately Exponential as well as Inverse quantitative data transformation performances respectively.
In addition, although findings revealed interesting performance with regard Logarithm, Box-Cox, Maximum-Minimum, Maximum, and Z-score and Square Root data transformation methods methodologies in term of adjusting data normal distribution, it is noteworthy to underline the intermediary role of Maximum-Minimum, Maximum and Z-score data transformation systems between (i) Logarithm and Box-Cox and (ii) Square Root quantitative data standardization procedures. Therefore, we provided an interacting analysis with regard several quantitative data transformation methodologies highlighting the link among them for evaluating data normality as well as data variance homogeneity.
Conclusion
Findings highlighted Z-score, Minimum-Maximum, and Maximum, Box-Cox, Square Root and Logarithm data transformation performances in reducing quantitative positive data variability as well as adjusting data normality. Even if results revealed Square Root data transformation as exhibiting intermediary behavior between
(i)Box-Cox and Logarithm and
(ii)Maximum-Minimum, Maximum, Z-score data transformation methodologies, it is noteworthy to underline the high performance of Box-Cox quantitative data transformation procedure in term of yielding better residual structure, displaying smaller bias transformation as well as transformed data normality.
The present study provided a systematic comparative study that highlighted difference as well as similitude between eight (8) quantitative data standardization methodologies providing useful tool to researchers, in choosing adequately data transformation methodologies that well fitting for their investigations.
Authors contributions
Noel Dougba Dago, Ph.D performed presently computational statistical analysis and as well write the paper. Mr. Kablan Gnoan Justin and Mr Dagnogo Dramane participated in analyzing statistical data respectively. All Authors have read and approved final version of the manuscript.
References
- CurranEverett D, Benos DJ (2004) Guidelines for reporting statistics in journals published by the American Physiological Society. Am J Physiol Endocrinol 287(2): E189-E191.
- Ghasemi A, Zahediasl S (2012) Normality Tests for Statistical Analysis: A Guide for Non-Statisticians. Int J Endocrinol Metab10(2):486-489.
- Altman DG, Bland JM (1995). Statistics notes: the normal distribution. BMJ 310 (6975):298.
- Driscoll P, Lecky F, Crosby M (2000). An introduction to everyday statistics-1. J AccidEmerg Med17(3):205-211.
- Pallant J (2007) SPSS survival manual, a step-by-step guide to data analysis using SPSS for windows. (3rdEdn). Sydney: McGraw Hill. p. 179-200.
- Field A (2009) Discovering statistics using SPSS. (3rdEdn). London: SAGE publications Ltd. p. 822.
- NIST/SEMATECH (2012) e-Handbook of Statistical Method.
- Feng C, Wang H, Lu N, Chen T, He H, et al. (2014)Log-transformation and its implications for data analysis. Shanghai ArcPsychiatry 26 (2): 105-109.
- Feng C, Wang H, Lu N, Tu XM (2012). Log-transformation: applications and interpretation in biomedical research. Stat Med 32: 230-239.
- Dago DN, Tuo Y, Niamien CJM, Moroh AJL, Dagnogo D, et al.(2019b) Intercropping Agricultural Practices by Improving Maize Early Growth Process: A Bio-Statistical Approach. Curr Res in Biost.9: 1.15 DOI: 10.3844/amjbsp.2019.1.15.10
- Zhou YH, Raj VR, Siegel E, Yu L (2010) Standardization of Gene Expression Quantification by Absolute Real-Time qRT-PCR System Using a Single Standard for Marker and Reference Genes. Biomark Insights 5:79‐85.
- Diarrassouba N, Dago DN, Soro S, Fofana IJ, Silué S, et al. (2015)Multi-variant statistical analysis evaluating the impact of rhizobacteria (Pseudomonas fluorescens) on growth and yield parameters of two varieties of maize (Zea mays L.). International Journal of Contemporary Applied Sciences2(7):206-224.
- Dago ND, Diarrassouba N, Nguessan AK, Lamine BM (2016) Computational statistics assessing the relationship between different rhizobacteria (Pseudomonas fluorescence) treatments in cereal cultivation. American Journal of Bioinformatics Research 6(1):1-13.
- Dodge Y (2003)The Oxford Dictionary of Statistical Terms, 1st, Oxford University Press. ISBN-10: 0198509944, pp: 498.
- Dago DN, Silué PD, Fofana IJ, Diarrassouba N, Lallié HNM, et al. (2015)Development of a Statistical Model Predicting Rice Production by Rain Precipitation Intensity and Water Harvesting. I J Recent Sci Res6(9): 6270-6276.
- Dago ND, Fofana IJ, Diarrassouba N, Barro ML, Moroh JLA, et al. (2019a)Quick Computational Statistical Pipeline Developed in R Programing Environment for Agronomic Metric Data Analysis. American Journal of Bioinformatics Research 9(1): 22-44.16
- Box GEP Cox DR (1964) An analysis of transformations. Journal of the Royal Statistical SocietySeri B 26: 211-234.
- Osborne J (2010) Improving your data transformations: Applying the Box-Cox transformation, Practical Assessment, Research, and Evaluation. 15, Article 12.
- Manly BFJ (1976) Exponential Data Transformations. Journal of the Royal Statistical Society: Series D (The Statistician) 25: 37-42.
- Luai AS, Zyad S, Basel K (2006) Data Mining: A Preprocessing Engine. J Computer Sci 2 (9): 735-739.
- Suzuki R and Shimodaira H (2006) Pvclust: an R package for assessing the uncertainty in hierarchical clustering, Bioinformatics 22 (12): 1540-1542.
- Suzuki R and Shimodaira H (2004) An application of multiscale boot strapre sampling to hierarchical clustering of microarray data: How accurate are these clusters? The Fifteenth International Conference on Genome Informatics P034.
- Shimodaira H (2004) Approximately unbiased tests of regions using multistep-multiscale bootstrap resampling. Annals of Statistics 32: 2616-2641.
- Sam SS, Martin BW (1965) An analysis of variance test for normality (complete samples). Biometrika 52(3):e4:591-611.
- Patrick R (1995) Remark AS R94: A remark on Algorithm AS 181: The W test for normality. Applied Statistics 44:547-551.
- Becker RA, Chambers JM, Wilks AR (1988) The New S Language. Wadsworth & Brooks/Cole.
- Kutner MH, Nachtsheim CJ, Neter J, Li W (2005) Applied linear statistical models (5th). Boston: McGraw-Hill Irwin. pp. 129-133.
- Altman DG and Bland JM (1996) Statistic Notes: Transforming data. BMJ 312(7033): 770.
- Schmidt AF and Finan C (2018) Linear regression and the normality assumption. J Clin Epidemiol98:146‐151.
- Royston P (1991) Estimating departure from normality. Stat Med 10(8):1283-1293.
- Oztuna D, Elhan AH, Tuccar E (2006) Investigation of four different normality tests in terms of type 1 error rate and power under different distributions. Turkish Journal of Medical Sciences 36(3):171-176.
- Kowalski J, Tu XM (2007)Modern Applied U Statistics. New York: Wiley.
- Tang W, He H, Tu XM (2012) Applied categorical and count data analysis. FL: Chapman & Hall/CRC.
- Christoph Fischer (2016) Comparing the Logarithmic Transformation and the Box-Cox Transformation for Individual Tree Basal Area Increment Models. For Sci 62(3):297-306.






























