Confidence Intervals for Relative Risk by Likelihood Ratio Test
Mai Zhou*
Department of Statistics, University of Kentucky, USA
Submission: February 19, 2018; Published: May 22, 2018
*Corresponding author: Mai Zhou, Department of Statistics, University of Kentucky, Lexington, KY 40536, USA; Email: maizhou@gmail.com
How to cite this article: Mai Zhou. Confidence Intervals for Relative Risk by Likelihood Ratio Test. Biostat Biometrics Open Acc J. 2018; 6(5): 555700. DOI:10.19080/BBOAJ.2018.06.555700
Abstract
In a recent article in this journal the authors compared four methods of constructing confidence interval for the relative risk. We aim to provide some more recent literature on this topic and propose to include in the comparison the alternative method of the Wilks confidence interval based on the likelihood ratio tests. We describe the procedure and provide R code for constructing such confidence intervals. No transformation is needed, and the procedure is known to often produce better confidence intervals in other settings [1]. AMS 2000 Subject Classification: Primary 60E15; secondary 60G30.
Keywords: Wilks theorem; Chi square distribution; Confidence interval; Likelihood Ratio; Relative Risk; Parameter space; Asymmetry; Explicit formula; Algorithm; Binomial random variables; Probabilities; Independent assumption; Maximizing; Wilks confidence; Invariant; Comprehensive; Distribution quantile; R code; BinoRatio; Test statistic
Introduction
The problem of constructing better confidence intervals for the risk ratio from a 2x2 table has a long history and is been considered by many authors. Related problem of confidence interval for the odds ratio and difference of risks are also been considered. Two relevant books are and [2,3]. The question of analyzing 2x2 table has its roots in the chi square test which dates back to at least 100 years. The book of Agresti has a chapter discuss the history of statistical analysis of 2x2 tables [3]. Yet the comparisons of different procedures for the confidence intervals for risk ratio keep appearing in the research journals; including a recent paper in this journal: the 2018 Mini review paper of BBOAJ [4-6].
I can see a few reasons why this is the case 1 the problem is important; case 2 there is no clear winner in the proposed confidence interval solutions. The performance of many proposed methods depended on the whereabouts of the true parameters, and sample sizes. Most confidence interval methods proposed fall into three groups: Wald confidence interval, coupled with some transformation, for example those in [1]; Score test and modified score test based confidence intervals; and lastly, the Wilks likelihood ratio test based confidence intervals. In this short note, besides provide some more recent literature on this problem, we call for more attention of the Wilks likelihood ratio test based confidence interval. For some reason, it has not been considered as extensively as the other two, and is missing in many numerical comparison studies [6,7]. The reason why this method has not been more popular, perhaps lie in the computational cost of the procedure, and non-explicit nature of the formula. But with the computing cost now down to almost nothing, and wide available of free high quality software like R, this should no longer be an issue. Both SAS proc freq and SAS proc genmod can compute the likelihood ratio based confidence interval. Some R software is provided in the companion website for the Agresti book [3], and a simple function to compute confidence interval for risk ratio is also available at the end of this paper or website.
The LRT method is transformation invariant
If you have a confidence interval for θ, say (lower; upper), and you want a confidence interval for 1/θ instead (or any other monotone function), you can find it by simply taking the inverse of the lower and upper bounds for θ, (1=upper; 1=lower). The consequence of this fact is that we do not have to ever worry about computing the confidence interval on another scale using some fancy transformations.
The LRT method is range preserving
This means that the confidence intervals it produces will always be inside of the parameter space. So, in the risk ratio case, the confidence intervals produced by the LRT method will always be between (0,∞).
You do not have to compute/estimate the variance of the estimator or test statistics.
The LRT method does not necessarily give symmetric intervals.
The asymmetry of the intervals is more similar to the actual distributions under consideration. On the other hand, the Wilks confidence interval do not have an explicit formula, it is an computer algorithm based method. This may not help in the sample size calculations.
Likelihood for the ratio of two success probabilities
Suppose we have two independent binomial random variables, X1, and X2, where X,1∽ Binomial(n1, p1) and X,2∽ Binomial(n2, p2). The MLE for p1, is 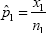 and the MLE for 2 is
and the MLE for 2 is 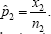 .Now Let's suppose that we want to use the likelihood ratio test method to create a confidence interval for the ratio
.Now Let's suppose that we want to use the likelihood ratio test method to create a confidence interval for the ratio 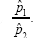 . Since maximum likelihood estimators are invariant, we know that the MLE for p1/p2 will simply be
. Since maximum likelihood estimators are invariant, we know that the MLE for p1/p2 will simply be 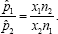 We also know that since independent assumption on the two sample made the log-likelihood ratio additive, it follows that LLR = LLR (sample1,)+ LLR (sample2), where
We also know that since independent assumption on the two sample made the log-likelihood ratio additive, it follows that LLR = LLR (sample1,)+ LLR (sample2), where
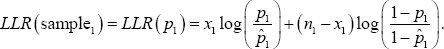
Since we want to use the likelihood ratio test for the ratio, we will need to consider the following hypotheses:

In the two sample log likelihood ratio, our initial parameters are p1, and p2. But this is equivalent to considering the parameters p1, and θ , since θ=p1/p2 If we take p1, and θ to be our parameters, then it follows that p, can be viewed as our nuisance parameter since θ is what we are truly interested in. We can get rid of a nuisance parameter in the log-likelihood ratio by simply profiling or "maximizing it out». In this case, we will have

And then we can multiply this by -2 to obtain our likelihood ratio test statistic for θ alone. We then can compare it to X, (a) and determine whether or not to reject Ho. Finally, we can create a confidence interval for θ=p1/p2 by finding the values of θ which give us a likelihood ratio test statistic less than 3:84. Below is the R code for computing a confidence interval for the ratio of two success probabilities using the likelihood ratio test method. Before execution the following commend, you need to key in the definition of the function Bino Ratio which is given at the end of this paper or from the website.
BinoRatio (nl = 100, xl = 30, n2 = 90, x2 = 33)
## $Low
## [1} 0.5420785
##
## $Up
## [1] 1.227019 ##
##
## FstepL
## [1] 6.103516e - 05
##
## $FstepU
## [1] 6.103516e - 05
##
## $Lvalue
## [1] 3.839973
##
## $Uvalue
## [1] 3.839915
From the output, we read that the 95% confidence interval for the ratio of θ=p1/p2 is [0.54208, 1.22702], if sample one having 30 successes in 100 trials and sample two having 33 successes in 90 trials.
Possible modifications to the wilks confidence intervals
While extensive modifications has been proposed for the score test base confidence intervals [6], I am not aware of modifications to the likelihood ratio test based confidence intervals. I can see at least the following possible modifications: replace the x2 quantile value by the square ofthe t distribution quantile, where the sample size is n + n2-1. For example, the X2 95% quantile 3.84 be replaced by (tt(0.025))2 for degrees of freedom k. similar to [5], simply add 2 to the number of success and add 4 to the number of trials before computing the likelihoods. modifications when we have either zero success or 100% success. This may be similar to the table in the [1], but with modification in this may not be necessary. Of course all these modified confidence intervals need to be carefully investigated in a comprehensive numerical study.
BinoRatio <- function(n1,x1,n2,x2){
if(x1>=n1)stop("all success(sample 1)?")
if(x2>=n2)stop("all success(sample 2)?")
if(x1<=0)stop("no success?")
if(x2<=0)stop("no success?")
MLE <- (x1*n2)/(x2*n1)
EPS <- .MachineSdouble.eps
llr <- function(const, n1, x1, n2, x2, theta){
npllik1 <- -2*(x1*log((const*n1)/x1)+
( n1-xl)*log ((((1 -cons t )*nl)/( nl-xl)))
npllik2 <- -2*(x2*log((n2*const/theta)/x2) +
(n2-x2)*log(((1-const/theta)*n2)/(n2-x2)))
retum(npllik1 + npllik2)
}
Theta <- function(theta,n1=n1,x1=x1,n2=n2,x2=x2){
upBD <- min(1-EPS, theta - EPS)
temp <- optimize(f = llr,
lower = EPS, upper = upBD,
n1=n1, x1=x1, n2=n2, x2=x2,
theta = theta)
cstar <- temp$minimum
val <- temp$objective
pvalue <- 1 - pchisq( val, df=1)
list(' -2LLR' = val, cstar = cstar, Pval=pvalue)
}
temp <- findUL(fun=Theta, MLE=MLE, n1=n1, x1=x1, n2=n2, x2=x2) return(temp)
}
findUL <- function(step = 0.01, initStep = 0, fun, MLE, level = 3.84, ...)
{
value <- 0
step1 <- step
Lbeta <- MLE - initStep
while (value < level) {
Lbeta <- Lbeta - step1
value <- fun(Lbeta, ...)$"-2LLR"
}
Lbeta0 <- Lbeta
Lbeta1 <- Lbeta + step1
tempfun <- function(beta){
return( level - fun(beta, ...)$"-2LLR" )
}
temp1 <- uniroot(tempfun, lower=Lbeta0, upper=Lbeta1)
Lbeta <- tempi$root
valuel <- level - tempi$f.root
value <- 0
Ubeta <- MLE + initStep
while (value < level) {
Ubeta <- Ubeta + step value <- fun(Ubeta, ...)$"-2LLR"
}
UbetaO <- Ubeta
Ubetal <- Ubeta - step
temp2 <- uniroot(tempfun, lowei=Ubeta1, upper=Ubeta0)
Ubeta <- temp2$root value <- level - temp2$f.root
return(list(Low = Lbeta, Up = Ubeta, FstepL=temp1$estim.prec,
FstepU =temp2$estim.prec, Lvalue = valuel, Uvalue = value))
}
References
- Alharbi N, Tsagris M (2018) Confidence Intervals for the Relative Risk. Biostat Biometrics Open Acc J 4(5): 555647.
- Fleiss J, Levin B, Paik M (2003) Statistical Methods for Rates and Proportions, (3rd edn). Wiley, USA.
- Agresti A (2013) Categorical Data Analysis (3rd edn). Wiley, USA.
- Price R, Bonett D (2008) Confidence intervals for a ratio of two independent binomial proportions. Statist Med 27(26): 5497-5508.
- Fagerland M, Lydersen S, Laake P (2015) Recommended confidence intervals for two independent binomial proportions. Stat Methods Med Res 24(2): 224-254.
- Agresti A, Ryu E (2010) Pseudo-score inference for parameters in discrete statistical models. Biometrika 97(1): 215-222.
- Agresti A, Caffo B (2000) Simple and Effective Confidence Intervals for proportions and difference of proportions result from adding two successes and two failures. Amer Stat 54(4): 280-288.






























