Mathematical Tomography
Armen Sergeev
Department of Mathematical Physics, Steklov Mathematical Institute, Russia
Submission: January 22, 2018; Published: May 22, 2018
*Corresponding author: Armen Sergeev, Department of Mathematical Physics, Steklov Mathematical Institute, Russia; Email: sergeev@mi.ras.ru
How to cite this article: Armen S. Mathematical Tomography. Biostat Biometrics Open Acc J. 2018; 6(5): 555697. DOI: 10.19080/BBOJ.2018.06.555697.
Keywords
Keywords: Tomography; Computerized tomography; Revolutionizing; Fluorography; Diagnostics; Roentgen rays; Compute era; Detectors; 3-dimensional picture; Radon's solution; Arbitrary function; Funk formula; Theoretical mathematics; Cormack algorithm; Non-trivial algorithms; Curved trajectories; Unique geodesic; Seismic waves; Velocity of propagation; Integral geometry; Sub manifolds
Introduction
Tomography and its early history
Computerized tomography is one of the most impressive scientific achievements of XXth century. It had a revolutionizing impact on the whole contemporary medical science and now it is difficult to imagine a serious medical hospital without a computerized tomograph. For its construction the physicists Allan Cormac and Godfrey Haunsfield were awarded in 1979 by the Nobel Prize in physiology and medical sciences. Let us recall what is computerized tomography. We all have passed through the Roentgen or X-ray diagnostics (called otherwise fluorography), say, of our breast. You are standing between the two vertical plates one of which is the source of X-rays while another one is the detector. As a result of such diagnostics you will obtain the two-dimensional projection of your breast on the detector plate, in other words its photo taken in Roentgen rays. If we can get the similar projections in different space directions then it would be possible to reconstruct with some accuracy the inner structure of your body. Such a reconstruction method was well known from the first half of XXth century and got the name of "tomography" (in Greek ”xo|ioa” means "section"). However, this method could be realized in full scale only after the arrival of compute era. Precisely by this reason the new reconstruction method is called the "computerized tomography". To take the computerized tomogram the patient is placed into a toroidal camera, surrounding the investigated part of his body. This camera contains both the sources and detectors of X-rays. The data obtained in the process of tomography characterize the decreasing of X-rays along a big set of straight lines piercing the investigated body in different directions lying in the plane of tomograph. If you want to get a 3-dimensional picture, you should move the body with respect to the camera thus reconstructing the body in different planes. From mathematical point of view the reconstruction of one plane section of the body reduces to the reconstruction of a function on the plane from its integrals along all possible straight lines. This classical problem was solved by Johann Radon in 1917. Let us describe the Radon's solution in more detail. For that we consider a transform, called now the Radon transform which associates with a function on the plane its integrals along all straight lines. Since the set of lines on the plane depends of two real parameters (the distance from the line to the origin and the angle between the line and real axis) we can pose the problem of existence of an inverse transform. Such inversion was found by Radon and it is given by an integral transform with the kernel given (in modern terms) by some generalized function or distribution (later on we shall consider this Radon's formula in more detail).
For the sake of historical justice I should point that before him another classical reconstruction problem was posed and solved by Paul Funk. Namely, suppose that we have an even function defined on the sphere in 3-dimensional space. By even function we mean a function which takes the same values in antipodal points of the sphere. Now the problem: is it possible to reconstruct such a function from its integrals along big circles (i.e. along equators of the sphere)? This problem was posed by Herman Minkowski and solved by him in principle with the help of decompositions by spherical functions (Minkowski’s solution was published posthumously in the volume of his selected papers in 1911). Later on in 1913 Paul Funk has found a more elegant solution of this problem using the Abel's integral transform. We note in passing that we cannot get rid of the evenness condition of the original function since in the case of an arbitrary function on the sphere the Funk formula will reconstruct not an original function. It will produce the function which values in the antipodal points of the sphere are equal to the half sum of the values of the original function in these points (in particular, in the case of an odd function taking the values in the antipodal points which differ only by the sign, this formula will produce the identical zero).
Mathematical meaning of Radon's formula
Several words on the sense of Radon's formula from the point of view of the theory of distributions. It is based on the formula of decomposition of the delta-function in "plane waves". We recall that a plane wave in the n-dimensional Euclidean space is given by a hyper plane with the normal m such that its wave front at any given moment is defined by the equation (w, x ) = const. The formula of decomposition of the n -dimensional delta-function s( x) in plane waves has a different form depending on the parity of the number n . For odd n’s it is written as
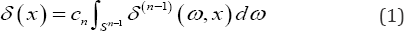
Where cn is an explicit function, depending only on the dimension of the space, s(n-1) (p) is the derivative of n-Vh order of the delta-function s(p), taken for p = (w,x), sn-1 is the unit sphere, and d® is its area element. For even n (in particular, in the case n = 2 we are interested in) the decomposition formula has another form

Where dn is also some explicit function, depending only on the dimension of the space. The kernel in this formula coincides with the regularization of the distribution pX, obtained by the analytic continuation of this function with respect to the complex parameter from the domain Re X> 0, where it is correctly defined, into the domain Re X< 0. The kernel in the formula (2) corresponds to the value of this distribution for p = (w,x), X = -n. Note that the formula (1) is local in contrast to the formula (2). The Radon inversion formula is obtained by the application of the formula (2) to the given function equal to the Radon transform of the original function.
X-ray tomography
Let us return to our X-ray tomograph. It seems that the Radon inversion formula resolves completely the problem of reconstruction of a given function from its integrals along straight lines. And it is indeed so on the level of theoretical mathematics. We have only to approximate the integral in Radon's formula by the discrete integral sum and everything is done: with the help of such approximation for any given an e > 0 we can reconstruct the original function from a discrete set of straight line with the given precision e. However the situation in practice is not that simple. As we have seen above, the kernel in the Radon inversion formula is a distribution which means that the integral of a given function with this kernel converges only in a weak sense. In practice it means that after the discretization such a convergence may be lost. By this reason the Cormack algorithm, realized in modern tomographs, is based on a completelydifferent inversion formula. Namely, to get this formula we first apply to a given function the one-dimensional Fourier transform along the direction, normal to the considered straight line being the argument of our function. As a result, we obtain the two-dimensional Fourier transform which may be inversed by the two-dimensional inverse Fourier transform.
This transform was extensively studied in the second half of XXth century. It can be realized using well-established modern computer algorithms. However, one should not think that this solves all our difficulties. The inversion of the Fourier transform, as also the majority of inverse problems, is illposed. And this results in many serious difficulties in the process of its realization on computers. We shall not speak about these problems here but it is necessary to have them in mind. We note only that the high cost of modern computerized tomographs is explained mostly not by the technological (hardwear) problems but rather by the incorporated non-trivial algorithms (softwear) which constitute the main commercial secret. The modern computerized tomographs can work in the real-time regime and are characterized by the high precision discovering the slightest differences in the density of the studied tissues (of order of fractions of a procent). Such a precision is sufficient to distinguish even the small cancer tissues at the beginning stage of their development.
Curvilinear radon transform and its applications
However, there are practical situations when the application of computerized tomography is not recommended because of the hardness of X-ray radiation (for example, it cannot be used to analyze the state of a pregnant woman). In such situations physicians prefer to use instead of X-rays less hard ultrasound rays. In contrast with X-rays, spreading along straight lines, the ultrasound waves propagatealong the curved trajectories. The corresponding mathematical problem can be formulated in the following way. Suppose that we have in the unit disk in the plane a conformally flat metric of the form
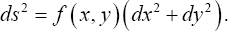
We can assume that this metric is sufficiently good in the sense that any two points on the unit circle are connected by a unique geodesic of our metric. (One can suppose, for example, that the considered metric is close to a flat one which guarantees the fulfillment of the above condition.) Assume that we know the lengths £(q>,y) of all geodesics, connecting the points on the circle with angle coordinates v and y. We would like to reconstruct the original metric, i.e. the function f (x, y), from these data. Since both functions depend on two real parameters, we can expect that this problem in principle can be solved. Indeed, it is proved that it is well-posed and correct which means that it has a unique solution and this solution depends continuously on the initial data. However, no explicit formula for such a solution, similar to that of Radon, is known.
Generalizing this problem, we can consider the curvilinear Radon transform which associates with a given function in the disk its integrals over geodesics of a given metric and try to find an inversion formula for such transform. It is clear that the problem of ultrasound reconstruction is a particular case of this inversion problem. Unfortunately, this inversion problem still remains unsolved despite many efforts of mathematicians. By this reason ultrasound tomographs use in the curvilinear case Radon's formula for the straight line case which implies, of course, a low precision of ultrasound tomographs compared to their X-ray prototypes (fortunately, this precision is sufficient to determine the gender of the future baby). The improvement of precision of ultrasound tomographs directly depends on the progress in solution of the mathematical problem, formulated above.
The curvilinear Radon inversion problem is important not only in the medicine but also, for example, in geology where it arises in the seismic methods of exploration of minerals. In the simplified form these methods work as follows. Assume that somewhere under the surface of the earth (mathematically, in the lower halfplane) we have an object (mineral) which we would like to localize. For that we arrange in different points of the surface of earth (mathematically, the real line) a series of micro explosions. The neighboring seismic stations fix the seismic waves coming from these explosions. The velocity of propagation of these waves allows to calculate the lengths of geodesics of the metric characterizing the object we are interested in. It remains only to solve the inversion problem for the arising curvilinear Radon transform in order to reconstruct the metric and so localize the desired mineral. Hence, in this case the progress in developing of seismic methods also depends on the solution of the inversion problem for the curvilinear Radon transform.
NMR tomography
In last years another type of tomography has got a wide recognition. I mean the NMR-tomography, using the nuclear magnetic resonance phenomena. In order to explain the essence of this effect let us consider the following physical situation. Suppose that we have the hydrogen atom kernel, consisting of one proton, in the external magnetic field B. The projection of the intrinsic magnetic moment (spin) of proton to the direction of magnetic field can have only two values s+ and S_which are equal by their absolute value and differ only by sign. If we want to transfer our proton from the state s_ with low energy to the state s+ with large energy we should apply to it the electromagnetic field with frequency determined by the difference of energies in both states. Originally proton is in the state S_ with low energy. After the application of electromagnetic field with given frequency proton absorbs the radiation quantum and transfers to the state s+ with larger energy. Then it emits this quantum returning to the original state. Suppose now that we want to investigate a body with a big number of hydrogen atoms (for example, a human body containing a large amount of water). Exposing it to the electromagnetic radiation with gradient in different directions, we register the signals coming from hydrogen atoms. From the intensity of these signals we can deduce the distribution of atoms in the investigated domain, hence, distribution of density in it.
Mathematically, the problem of reconstruction of density distribution reduces to the inversion of the three-dimensional Fourier transform and is solved by the methods, analogous to those already used in the X-ray tomography. However, in contrast with X-ray tomography, in NMR-case we can use not the hard Roentgen radiation, dangerous for some patients, but more soft one, say, radio waves. Also this reconstruction can be made in the real-time regime which allows to analyze, for example, the work of a pianist brains while he is playing piano. The invention and elaboration of the NMR-tomography was marked by six Nobel prizes in physics and chemistry altogether (the first prize was awarded to Felix Bloch and Edward Purcell in physics). We have presented several examples of usage of mathematical tomography in medicine and geology. In fact, there many more and there still many problems to solve in this science.
Integral geometry
All formulated problems belong to a mathematical discipline called the integral geometry. The first general statement of such type relates to the reconstruction of a function in the n -dimensional space from its integrals along hyper planes. This problem was posed and solved by Johann Radon in the beginning of XXth century. In honour of Radon the transform, associating with a function its integrals along hyperplanes, is called the Radon transform. The further analysis and generalization of this transform led to the creation of a new mathematical discipline under the name of "integral geometry". The main problem, studied in this science, is the reconstruction of a function on a manifold from its integrals over the sub manifolds from a given family. The foundations of this science were layed down, on one side, by the members of Moscow school of functional analysis, represented by I.M. Gelfand, G.E. Shilov, M.I. Graev, S.G. Gindikin and others and on the other side by S. Helgason, A. Koranyi and their students. We have given above a non-trivial example of the problems in integral geometry, related to the curvilinear Radon transform which associates with a function in the disk its integrals along geodesics of a conformally flat metric.
The first step in the solution of the inverse problem of reconstruction of a function from its integrals along sub manifolds is the analysis of the so called direct problem consisting in the description of the image of Radon transform. The conditions to which the function, belonging to this image, are called, following Gelfand, the Cavalieri conditions. Their description is a difficult mathematical problem alreadyin the case of the Radon transform associating with a function in the n -dimensional space its integrals along all k -dimensional planes with k < n . For the curvilinear Radon transform, mentioned above, the Cavalieri conditions were found only recently by D.A. Popov.
Another range of the problems, studied in integral geometry, is related to the reconstruction of a surface from its geometric characteristics (for example, the curvature). A similar problem arises when we want to reconstruct a convex body from, say, the curvature of its plane sections. Such problems first arose in the works of classical geometers, such as Hermann Minkowski and Wilhelm Blaschke. Their solution is usually reduced to the solution of complicated nonlinear partial differential equations (such as Monge-Ampere equation). A big progress in their solution was achieved grace to the efforts of A.V. Pogorelov. There are sure that any progress in their solution will find important are still many unsolved problems in integral geometry but we practical applications.






























