Biostatistics and Biometrics Open Access Journal

Prediction of Strong Ground Motion Using Fuzzy Inference Systems Based on Adaptive Networks

Mostafa Allameh Zadeh^1*, Gholam Javan Doloiee¹ and Ali Nasrollahnejad²

¹Assistance Professor, International institute of seismology and earthquake engineering, Iran

²Phd student, International institute of seismology and earthquake engineering, Iran

Submission: December 12, 2017; Published: April 18, 2018

*Corresponding author: Mostafa Allameh Zadeh, Assistant professor, International Institute of Earthquake Engineering and Seismology (IIEES), Iran, Email: zadeh66@hotmail.com

How to cite this article: Mostafa Allameh Zadeh, Gholam Javan Doloiee, Ali Nasrollahnejad. Prediction of Strong Ground Motion Using Fuzzy Inference Systems Based on Adaptive Networks. Biostat Biometrics Open Acc J. 2018; 6(1): 555680. DOI: 10.19080/BBOAJ.2018.06.555680

Abstract

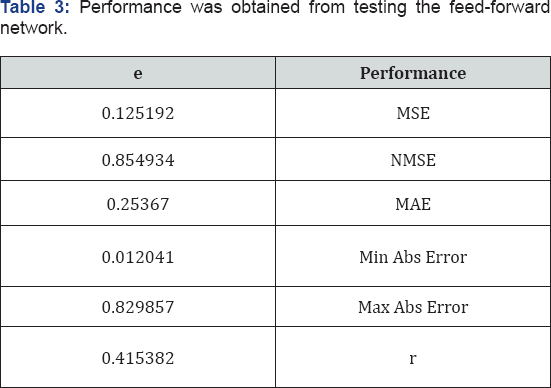
Peak ground acceleration (PGA) estimates have been calculated in order to predict the devastation potential resulting from earthquakes in reconstruction sites. In this research, a training algorithm based on gradient descent were developed and employed by using strong ground motion records. The Artificial Neural Networks (ANN) algorithm indicated that the fitting between the predicted strong ground motion by the networks and the observed PGA values were able to yield high correlation coefficients of 0.78 for PGA. We attempt to provide a suitable prediction of the large acceleration peak from ground gravity acceleration in different areas. Methods are defined by using fuzzy inference systems based on adaptive networks, feed-forward neural networks (FFBP)by four basic parameters as input variables which influence an earthquake in regional studied. The affected indices of an earthquake include the moment magnitude, rupture distance, fault mechanism and site class. The ANFIS network — with an average error of 0.012 — is a more precise network than FFBP neural networks. The FFBP network has a mean square error of 0.017 accordingly. Nonetheless, these two networks can have a suitable estimation of probable acceleration peaks (PGA) in this area.

Keywords: Adaptive-network-based fuzzy inference systems; Feed-forward back propagation error of a neural network; Peak ground acceleration; Rupture distance

Abbreviations: PGA: Peak ground acceleration; ANN: Artificial Neural Networks; FFBP: Feed-Forward Neural Networks; FIS: Fuzzy Inference System; Mw: Moment Magnitude

Introduction

Peak ground acceleration is a very important factor that must be considered in any construction site in order to examine the potential damage that can result from earthquakes. The actual records by seismometers at nearby stations may be considered as a basis. But a reliable method of estimation may be useful for providing more detailed information of the earthquake’s characteristics and motion [1]. The peak ground acceleration parameter is often estimated by the attenuation of relationships and also by using regression analysis. PGA is one of the most important parameters, often analyzed in studies related to damages caused by earthquakes [2]. It is mostly estimated by the attenuation of equations and is developed by a regression analysis of powerful motion data. Powerful motions relating to a ground have basic effects on the structure of that region [3]. Peak ground acceleration is mostly estimated by attenuation relationships [4]. The input variables in the constructed artificial neural network model are the magnitude, the source-to-site distance and the site’s conditions. The output is the PGA. The generalization capability of ANN algorithms was tested with the same training data. Results indicated that there is a high correlation coefficient (R²) for the fitting that is between the predicted PGA values by the networks and those of the observed ones. Furthermore, comparisons between the correlations by the ANN and the regression method showed that the ANN approach performed better than the regression. Developed ANN models can be conservatively utilized to achieve a better understanding of the input parameters and their influence, and thus reach PGA predictions.

Kerh & Chaw [1] used software calculation techniques to remove the lack of certainties in declining relations. They used the mixed gradient training algorithm of Fletcher-Reeves’ back propagation error [5]. They applied three neural network models with different inputs including epicentric distance, focal depth and magnitude of the earthquakes. These records were trained and then the output results were compared with available nonlinear regression analysis. The comparisons demonstrated that the present neural network model did have a better performance than that of the other methods. From a deterministic point of view, determining the strongest level of shaking- that can potentially happen at a site- has long been an important topic in earthquake science. Also, the maximum level of shaking defines the maximum load which ultimately affects urban structures.

From a probabilistic point of view, knowledge of the greatest ground motions that can possibly occur would allow a meaningful truncation of the distribution of ground motion residuals, and thus lead to a reduction in the computed values pertaining to probabilistic seismic hazard analyses. Particularly, it points to the low annual frequencies that exceed norms which are considered for critical facilities [6,7]. Empirical recordings of ground motions that feature large amplitudes of acceleration or velocity play a key role in defining the maximum levels of ground motion, which outline the design of engineering projects, given the potentially destructive nature of motions. They also provide valuable insights into the nature of the tails that further distribute the ground motions.

Feed-forward, back propagation error in neural networks

Artificial neural networks are a set of non-linear optimizer methods which do not need certain mathematical models in order to solve problems. In regression analysis, PGA is calculated as a function of earthquake magnitude, distance from the source of the earthquake to the site under study, local condition of the site and other characteristics that are linked to the earthquake source such as slippery length and reverse, normal or wave propagation. In non-linear regression methods, non-linear relations which exist between input and output parameters are expressed as estimations, through statistical calculations within a specified relationship [8]. One of the most popular neural networks is the back propagation algorithms. It is particularly useful for data modeling and the application of predictions [9] (Equations 1, 2 and 3). It is a supervised learning technique which was first described by Werbos [10] and further developed by Rumelhart et al. [11]. Furthermore, its most useful function is for feed forward neural networks where the information moves in one direction only, forward, beginning from the input nodes through to the hidden nodes, and then to the output nodes. There are no cycles or loops in the network.

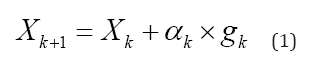
In (1), one instance of iteration is written for the back propagation algorithm. Where X_k is a vector of current weights and biases, gk is the current gradient and a is the learning rate.

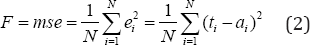
In (2), where F is the performance function of error (mean square error),'t' is the target and 'a' is the real output

In (3), 'a' is the net output,(n) is the net input and 'f' is the activation function of the neuron model

In (4), the error of energy is calculated by the least squares estimate for back-propagation learning algorithm. Where N is the number of training patterns, m is the number of neurons in the output layer. And tjk is the target value of processing the neuron. Therefore, this algorithm changes synaptic weights along with the negative gradient of the error energy function. Furthermore, it mostly benefits feed-forward neural networks where the information moves in only one direction, forward, beginning from the input nodes, through to the hidden nodes, and then to the output nodes. There are no cycles or loops in the network. The basic back-propagation algorithm adjusts the weights in the steepest direction of descent wherein the performance function decreases most rapidly. This network is a general figure of a multi-layer Prospectron network with one or several occasions of connectivity. Theoretically, it can prove every theorem that can be proven by the feed-forward network. Also, problems can be solved more accurately by testing general feed-forward networks.

Results of FFBP neural network

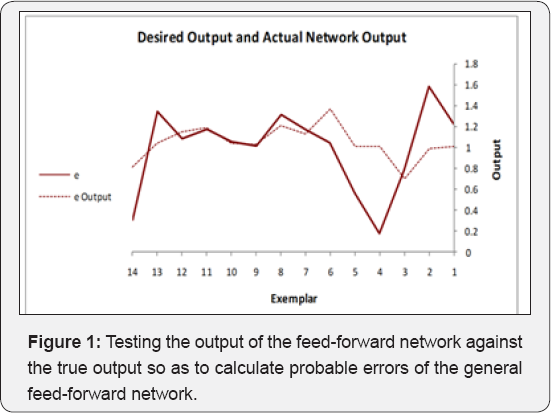
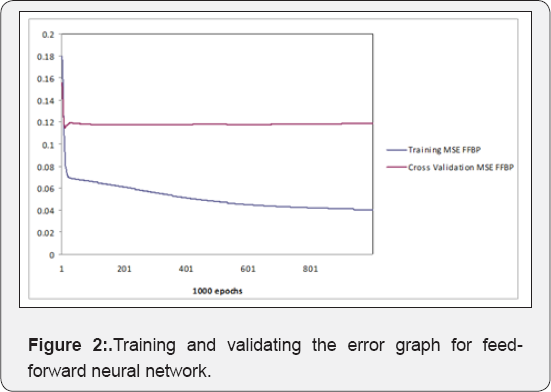
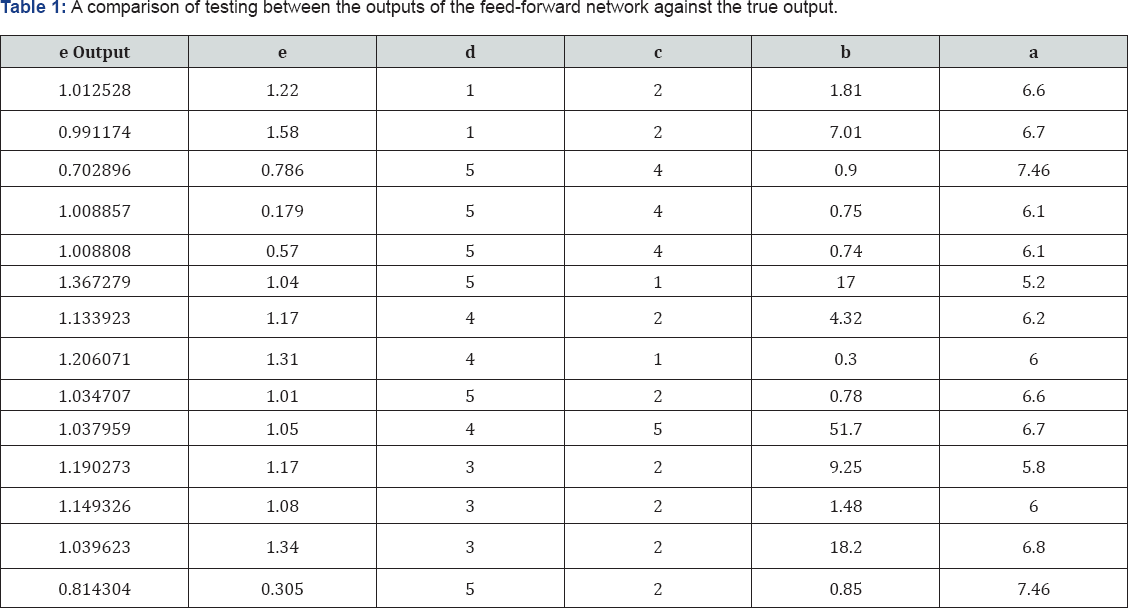
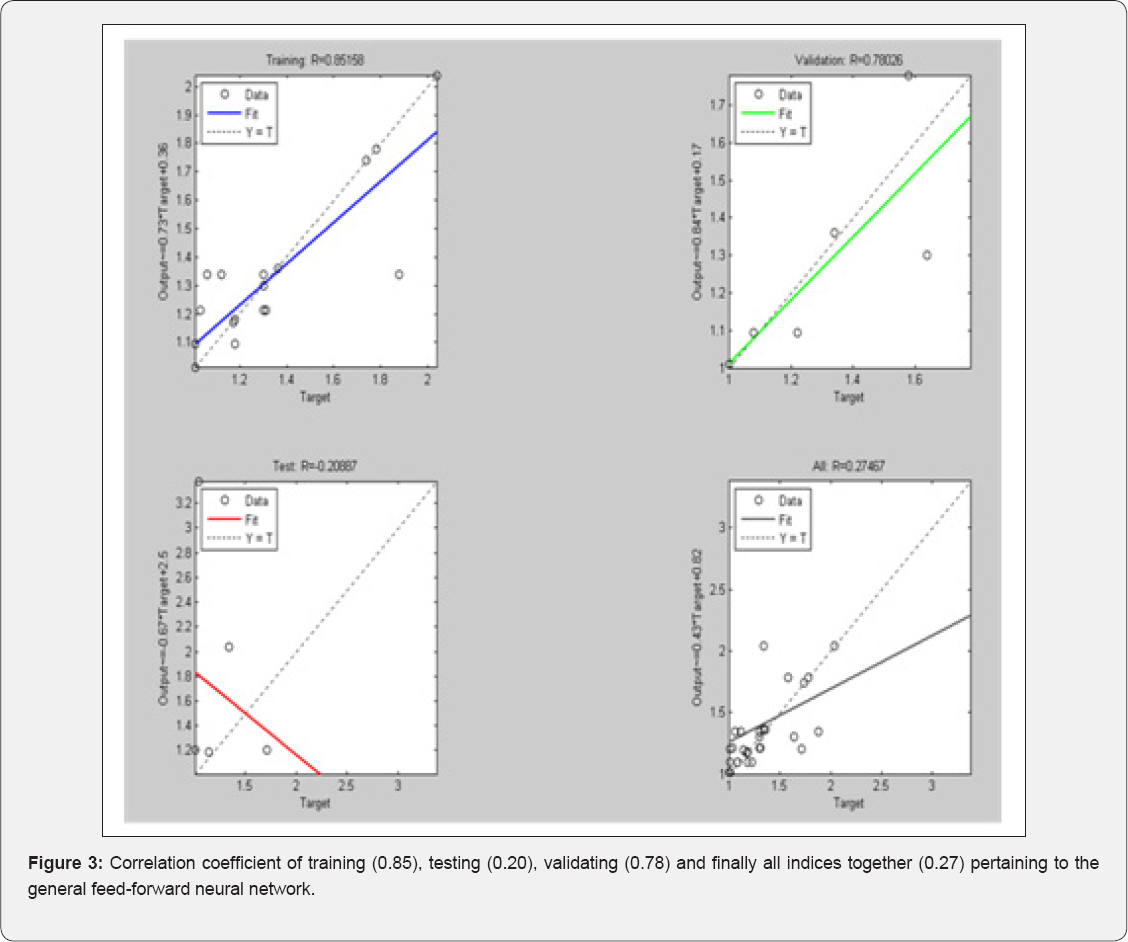
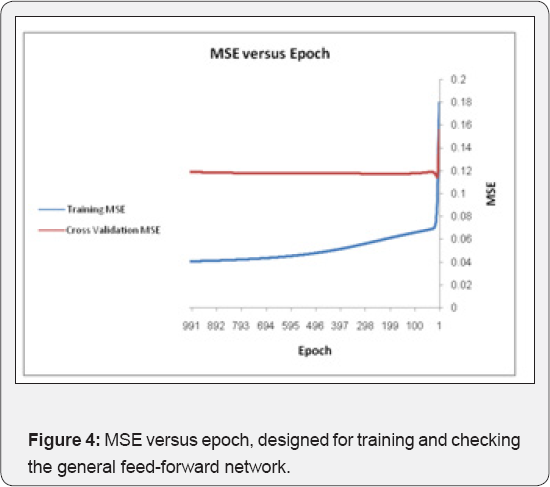
In Figure 1, testing the output of feed-forward neural networks against the true output is demonstrated. In Figure 2, the correlation coefficient of training, testing and validating general feed-forward neural networks is shown. In Table 1, testing the output of a feed-forward network against its true output has been compared. In Figure 3, training and validating the error graph against the feed-forward neural network is shown. Mean square error versus epoch is shown in Figure 4 with the aim of training and checking the general feed-forward

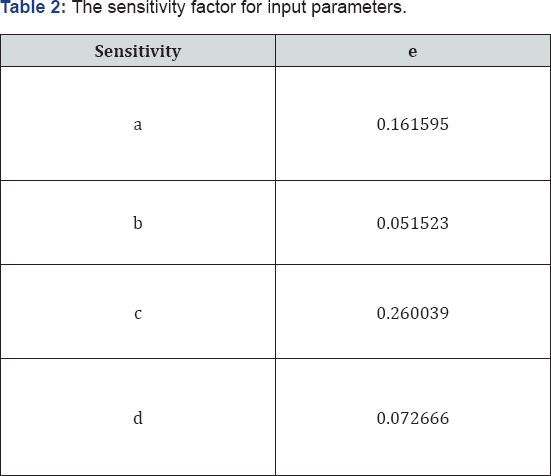
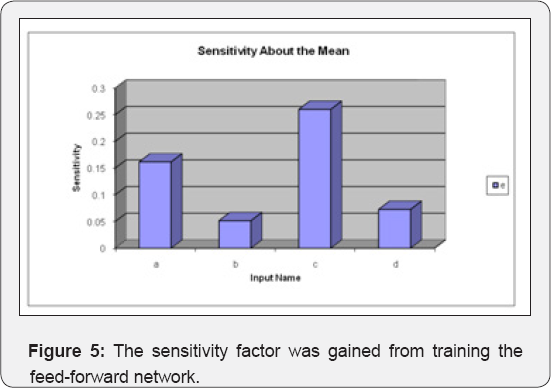
network. The sensitivity factor was obtained by training the feed-forward network (Figure 5). The sensitivity factor for input parameters is shown in Table 2. The performance error function was obtained by testing the FFBP neural network (Table 3).

Data processing

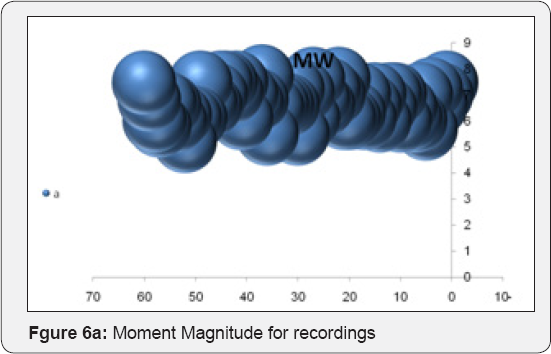
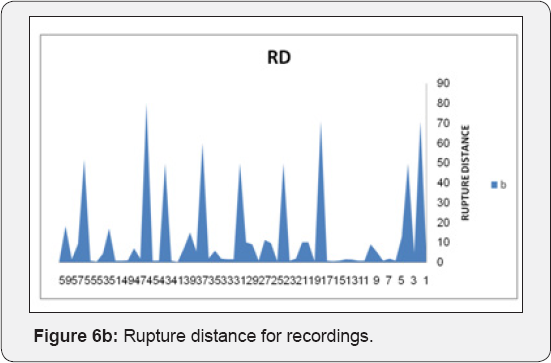
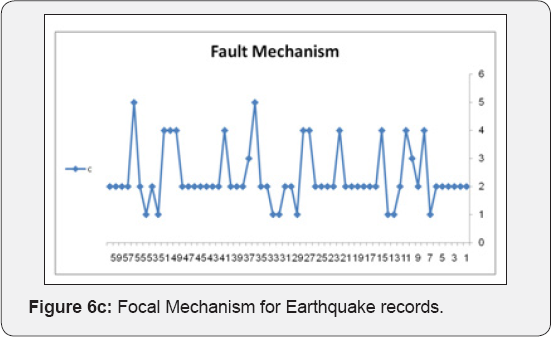
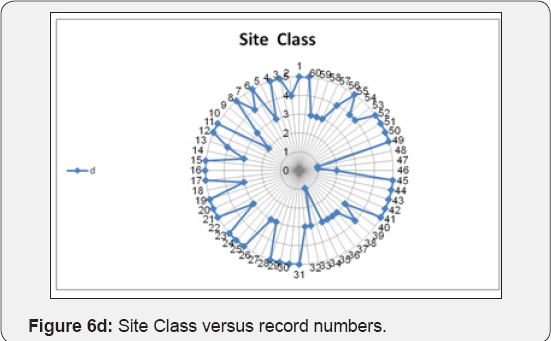
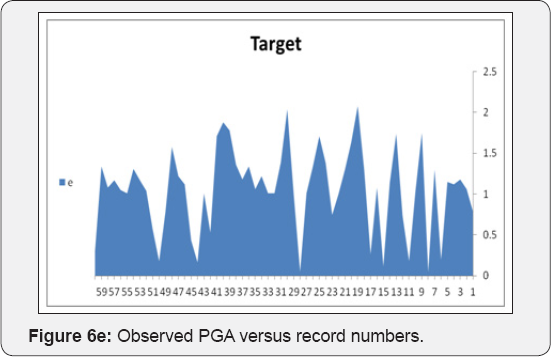
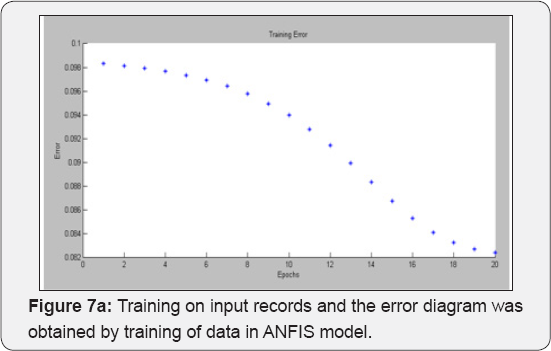
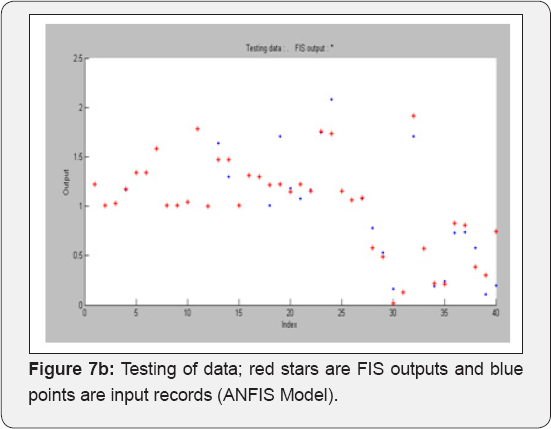
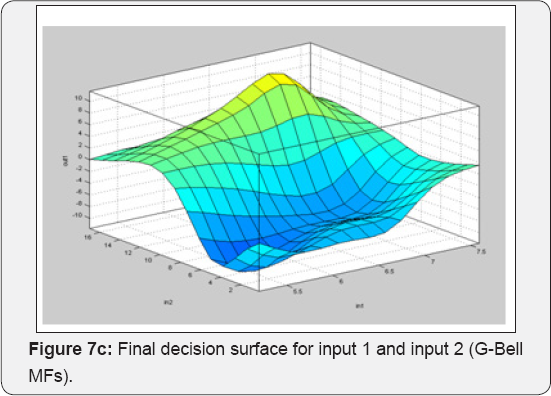
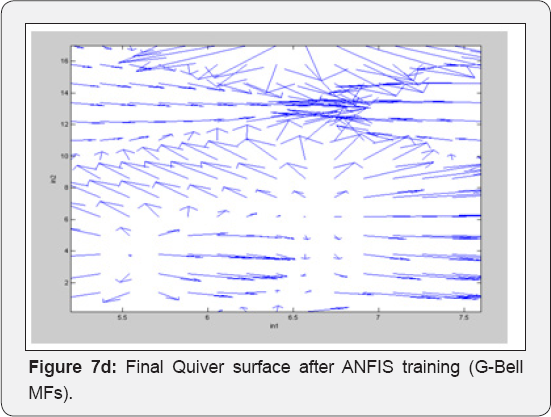
The datasets of records by large amplitude considered in this study involves one sets of accelerogram selected based on their value of PGA. These records are described below in terms of the variables generally considered to control the behavior of ground motions in general i.e. Magnitude, Rupture distance, style of faulting and site classification. The dataset includes recordings from events with Moment Magnitude ranging from (5.2-7.7) and rupture distance from (0.3-51.7 km). The SC values in the models were used as (1 to 5) for S-Wave velocity (For (1), Vs>1500 m/s and (5) Vs<180m/s). One Model was developed for each ANN method. This model was developed for estimation of maximum PGA values of the three components. The Focal Mechanism values in this model were used as (1 to 5) that (1: Strike Slip, 2:Reverse, 3:Normal, 4:Reverse oblique and 5: Normal oblique). A program includes MATLAB Neural Network toolbox was coded to train and test the models for each ANN method. All recordings from crustal events correspond to rupture distances shorter than 25km. The horizontal dataset shows a predominance of records from strike-slip and reverse earthquakes. Ground motions recorded on early strong-motions instruments often required a correction to be applied to retrieve the peak motions, Filtering generally eliminates the highest frequencies for motions recorded on modern accelerographs, and thus reduces the observed PGA values. The training of networks was performed using 60 sets of data. Testing of networks was done using 14 datasets that were randomely selected among the whole data. As shown in Figure 6 (a,b), the Mw and RD values of test and train data varied in the range of (5.2-7.7) and (0.3-52 km), respectively, the fault mechanism values were given in the Figure 6c. Figure 6d illustrated the site conditions of train and test data. As seen in this figure the site conditions were commonly soft and stiff soil types. Figure 6e showed the maximum PGA of records of the three components. In ANFIS model, training and the testing of records are shown in Figures 7a,b. Final decision surfaces are shown in Figure 7c. Final quiver surfaces are shown in Figure 7d.

Adaptive network based fuzzy inference system

The fuzzy logic appeared parallel to the growth in evolution of neural networks theory. The definition of being fuzzy can be found in human decision-making. These definitions can be searched by methods related to processing information [12].ANFIS is one of hybrid neuro-fuzzy inference expert systems and it works like the Takagi-Sugeno-type fuzzy inference system, which was developed by Jang [13]. ANFIS has a similar structure to a multilayer feed-forward neural network, but the links in an ANFIS can only indicate the flow direction of signals between nodes. No weights are associated with the links [14]. ANFIS

architecture consists of five layers of nodes. Out of the five layers, the first and the fourth layers consist of adaptive nodes while the second, third and fifth layers consist of fixed nodes. The adaptive nodes are associated with respective parameters, while the fixed nodes are devoid of any parameters [15-17]. For simplicity, we assume that the fuzzy inference system under consideration has two inputs x, y and one output called z. Supposing that the rule base contains two fuzzy if-then rules(6 and 7) of the Takagi & Sugenos [18], then the type-1 ANFIS structure can be illustrated as in Figure 6.

Rule 1: If (x is A1) and (y is B1) then (f = p_lx + q_ly + r₁) (5)

Rule 2: If(x is A2) and (y is B2) then (f₂ = p₂ x + q₂ y + r₂) (6)

Where x and y are the inputs, A, B_i are the fuzzy sets and ^fi is the output within the fuzzy region specified by the fuzzy rule. Then ^p_i ^{, q}i and ^r are the design parameters that are determined during the training process, in which a circle indicates fixed nodes, whereas a square indicates adaptive nodes.

The node functions which are in the same layer are of the same function family as described below:

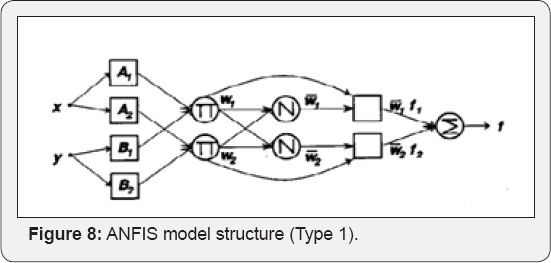
In Figure 8, layer (1), every node (i) is a square node with a node function like this: O¹_i=μ^Ai_(x)

The outputs of this layer constitute the fuzzy membership grade of the inputs, which are presented as:

Where x and y are the inputs that enter node (i), A is a linguistic label and m (x),mBi (y) can adapt any fuzzy membership function.(a,b and c) are the parameters of the membership function. As the values of these parameters change, the bell shaped function varies accordingly. In layer 2 (Figure 8), every node is a circle node labeled n. The outputs of this layer can be presented as a firing strength of rule. In layer 3, every node is a circle node labeled N. The '^th’ node calculates the ratio of the ‘i^th ’ rules' firing strength to the sum of all rules belonging to the firing strength. For convenience, outputs of this layer will be termed as normalized firing strengths. In layer 4, the defuzzification layer is an adaptive node with one node. The output of each node in this layer is simply a first order polynomial.

Where W_i is the output of layer 3, {^pi * * ^ri} is the parameter set. Parameters in this layer will be referred to as consequent parameters. In layer 5,the summation neuron is a fixed node which computes the overall output as the summation of all incoming signals. The single node in this layer is a circle node labeled E that computes the overall output as the summation of all incoming signals.

Functionally, there are almost no constraints on the node functions of an adaptive network except in the case of a piecewise differentiability. Structurally, the only limitation of network configuration is that it should be of the feed-forward type. Due to minimal restrictions, the applications of adaptive networks are immediate and immense in various areas. In this section, we propose a class of adaptive networks which are functionally equivalent to fuzzy inference systems. The targeted architecture is referred to as ANFIS, which stands for Adaptive Network-based Fuzzy Inference System. ANFIS utilizes a strategy of hybrid training algorithm to tune all parameters. It takes a given input/output data set and constructs a fuzzy inference system which has membership function parameters that are tuned, or adjusted, using a back-propagation algorithm in combination with the least-squares type of method (NAZMY .T.M, 2009). Fuzzy inference systems are also known as fuzzy- rule-based systems, fuzzy models, fuzzy associative memories or fuzzy controllers, when used as controllers. Basically, a fuzzy inference system is comprised of five functional blocks.

a. A rule base containing a number of fuzzy if-then rules.

b. A database which defines the membership functions of the fuzzy sets used in the fuzzy rules.

c. A decision-making unit which performs inference operations on the rules.

d. A fuzzification interface which transforms the crisp inputs into degrees of match with linguistic values.

e. A defuzzification interface which transform the fuzzy results of the inference into a crisp output.

Usually the rule base and database are jointly referred to as the knowledge base. The steps of fuzzy reasoning performed by fuzzy inference systems are:

a. To compare the input variables with the membership functions on the premise part so as to obtain the membership values. (That is the fuzzification step).

b. To combine multiplications or minimizations of the membership values on the premise part so as to yield the firing strength of each rule.

c. To generate the qualified consequence— either fuzzy or crisp — of each rule depending on the firing strength.

d. To aggregate the qualified consequences so as to produce a crisp output. (That is the defuzzification step).

Results ofANFIS network for maximum PGA simulation

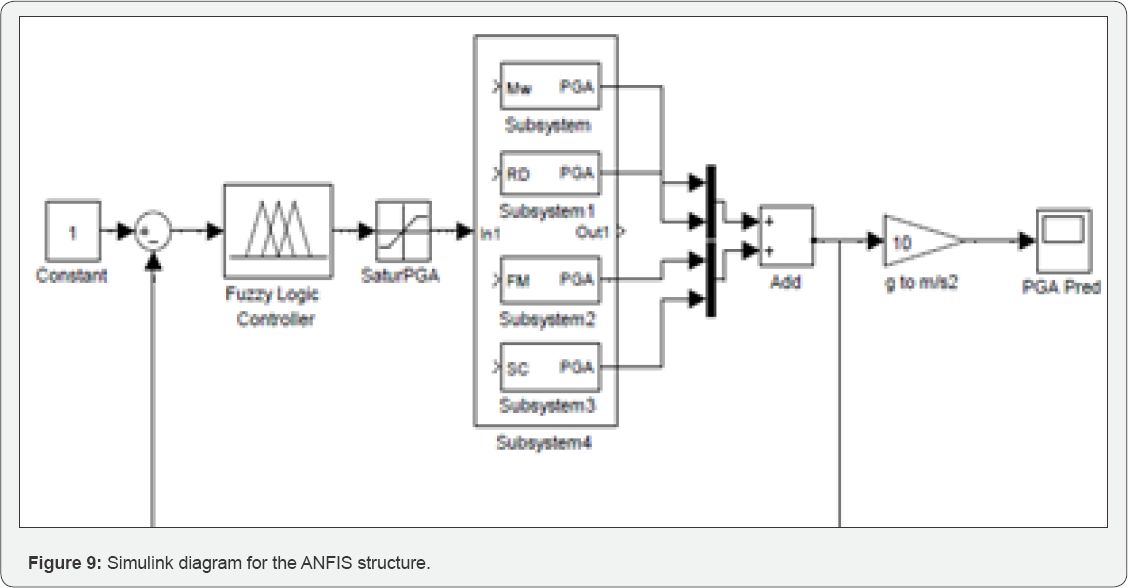
In this research, an adaptive neuro-fuzzy inference method was applied to simulate non-linear mapping among acceleration peak conditions. The neuro-fuzzy model included an approximate fuzzy reasoning through a sugeno fuzzy inference system (FIS). The input space was fuzzified by a grid-partitioning technique. A hybrid learning algorithm was selected in order to adapt the model's parameters. Furthermore, a linear-nonlinear regression analyses and neural network model were employed to observe the relative performances. Based on our findings, it can be concluded that the neuro-fuzzy control system exhibits a superior performance, compared to the other employed methods [19,20]. In the developed ANFIS model, input-space fuzzification was carried out via the grid-partitioning technique. Fuzzy variables were divided into four triangular membership functions *i>*₂> ^x3* 3. The 625 fuzzy ‘if-then’ rules were set up where in the fuzzy variables were connected by the T-Norm (AND) apparatus. First order sugeno FIS was selected for the approximate reasoning process. The adjustment of independent parameters was made according to the batch mode based on the hybrid learning algorithm. The ANFIS model was trained for 50epochs until the observed error ceased to fluctuate. The resultant neuro-fuzzy Simulink model structure is illustrated in Figure 9.

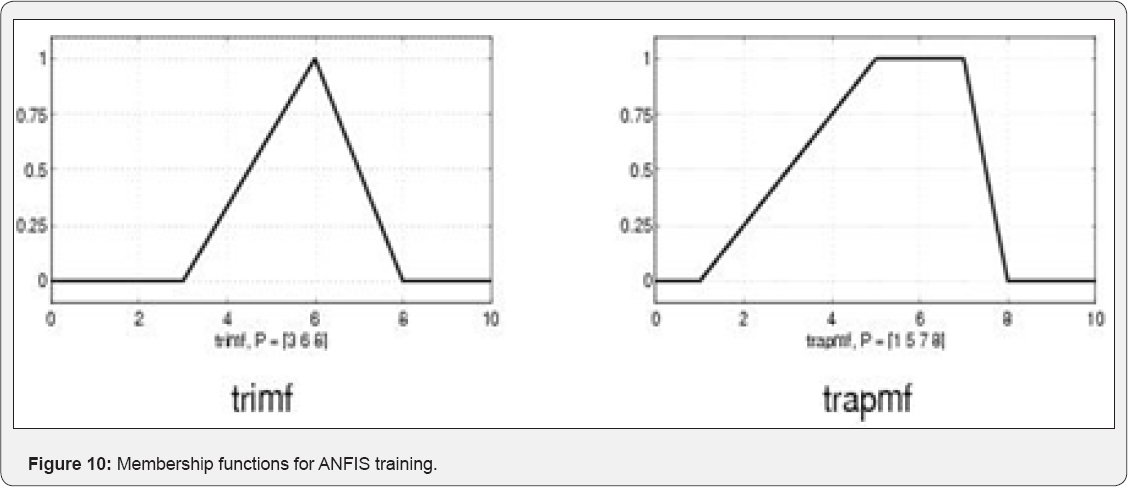
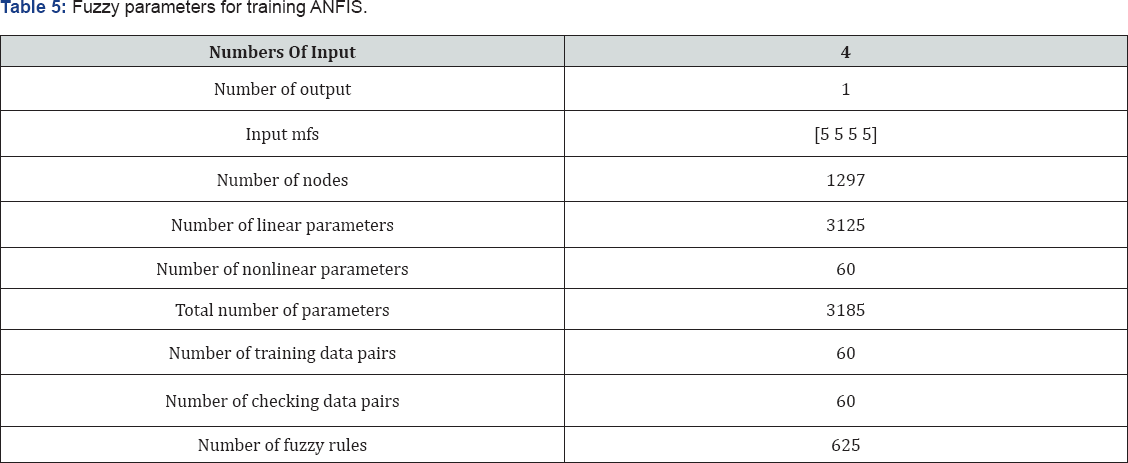
The input space contains four parameters- moment magnitude (Mw), rupture distance, fault mechanism and site class. The output contains vertical components of PGA, including 40 records from different regions of the world, 24 records for training, 6 records for checking and 10 records for testing the selected ANFIS network. Sixty training data and sixty checking data pairs were obtained at first. The one used here contains 625 rules, with four membership functions being assigned to each input variable, having total number of 3185 fitting parameters which are composed of 60 premise parameters and 3125 consequent parameters. This section presents the simulation results of the proposed type-3 ANFIS with both batch (off-line) and pattern (on-line) learning. In the first example, ANFIS is used to model highly nonlinear functions, where by results are compared with the neural network approach and also with relevant earlier work. In the second example, the FIS name is PGA1 and the FIS type is sugeno. We used the 'and-or' method for input partitioning. Furthermore, we used ‘wtsum’ and 'wtaver' functions for defuzzification. The ranges of input and output variables- in other words, the target variables- are Mw=(5-8), R=(1.50-80 km), fault mechanism type =(1-5),site class=(1-5) and target range (PGA)=(0.5-2.50). The number of MFs={5 5 5 5}, the MF type=Trimf and G-bell MFs (Figure 9 $10). The result of this simulation is LSE: 0.002 and the final epoch error equals to 0.0000002.

Results of the ANFIS network

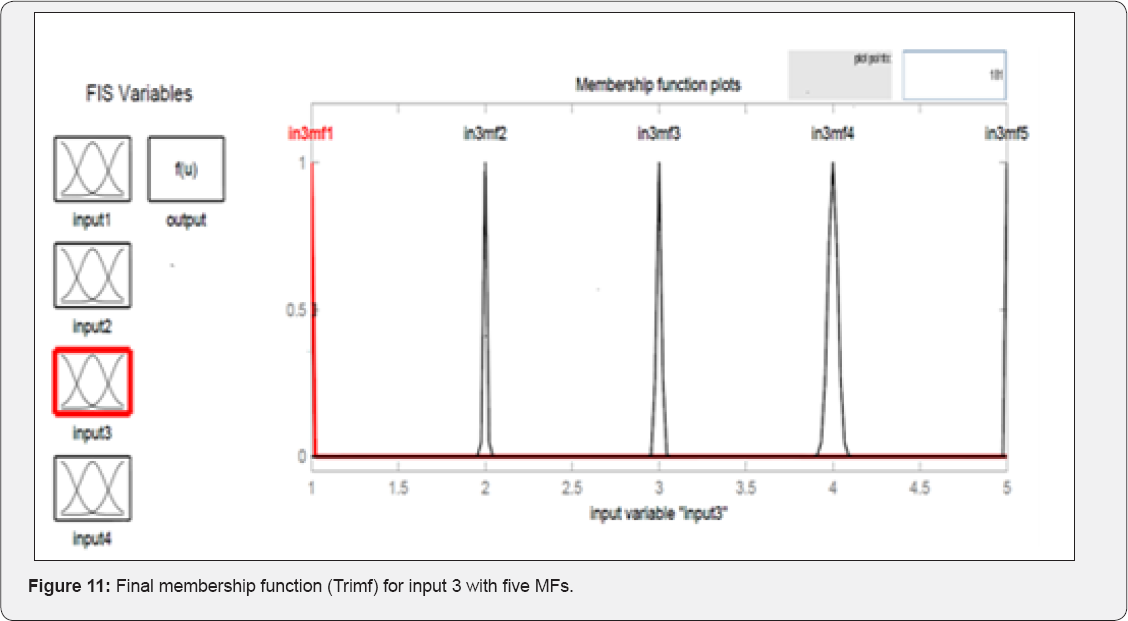
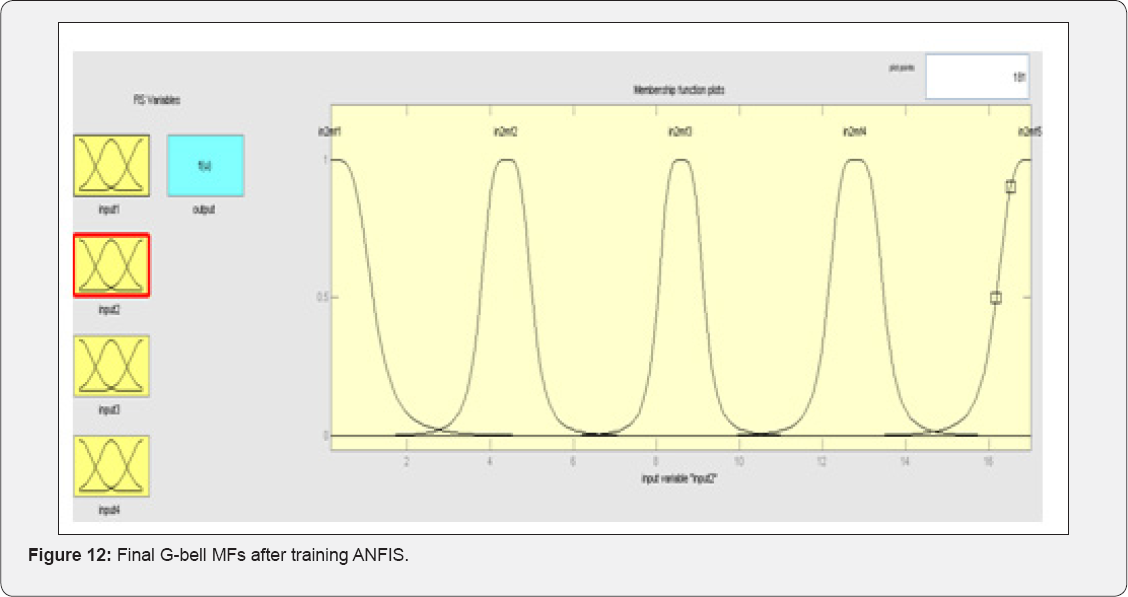
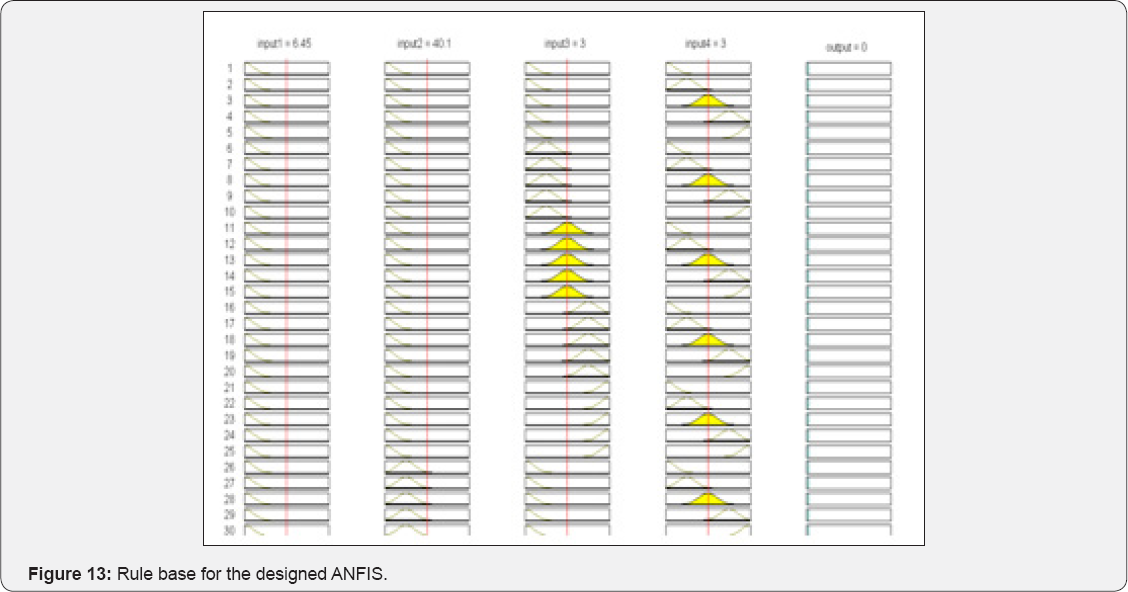
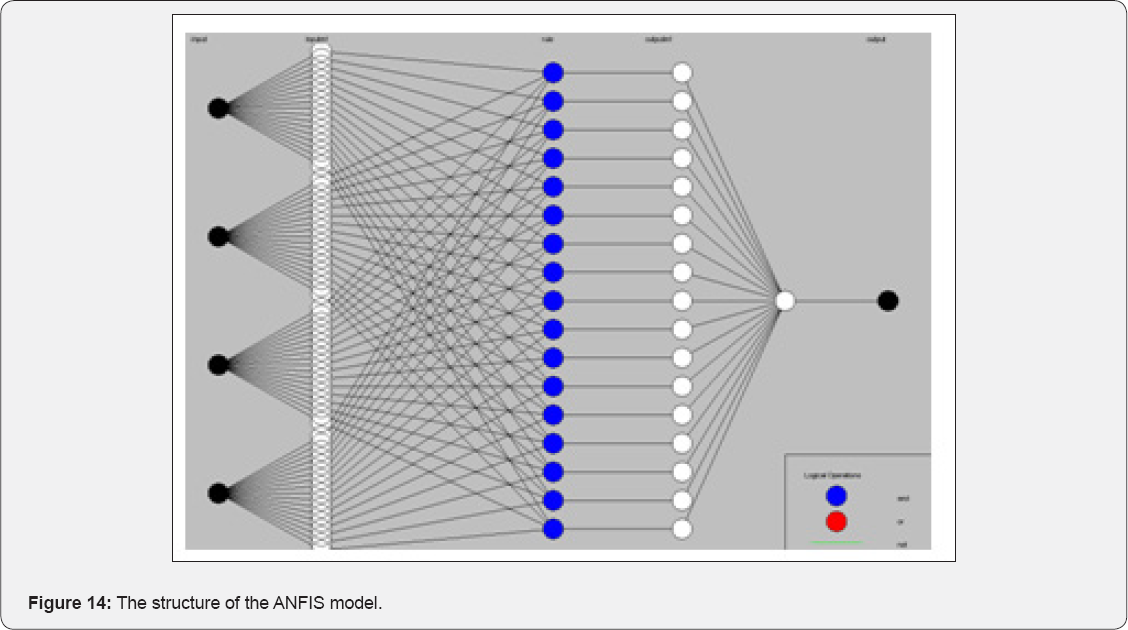
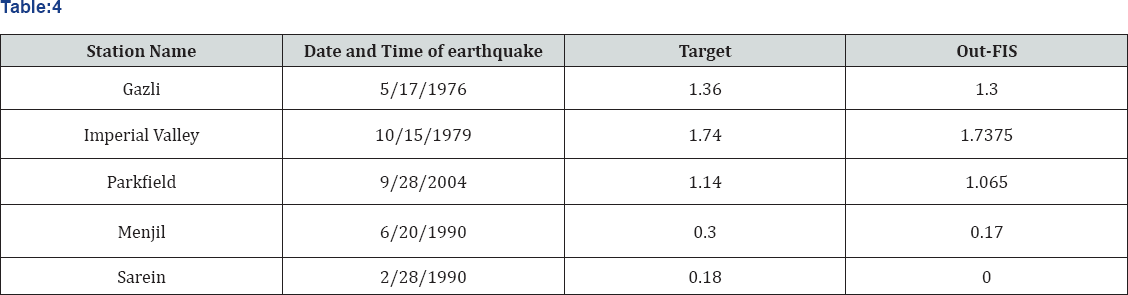
The input MFs for initial fuzzy inference system and the MFs of trained FIS are shown in Figure 11 & 12. The rule base for the designed ANFIS is shown in Figure 13. Finally, a trained FIS structure is created from the initial FIS by using the ANFIS GUI editor, which is depicted in Figure 14. Also, by testing the results, one can interpret Table 4. Fuzzy parameters used for training ANFIS are shown in Table 5. Also two membership functions for ANFIS training are shown in Figure 10.

Discussion on Results

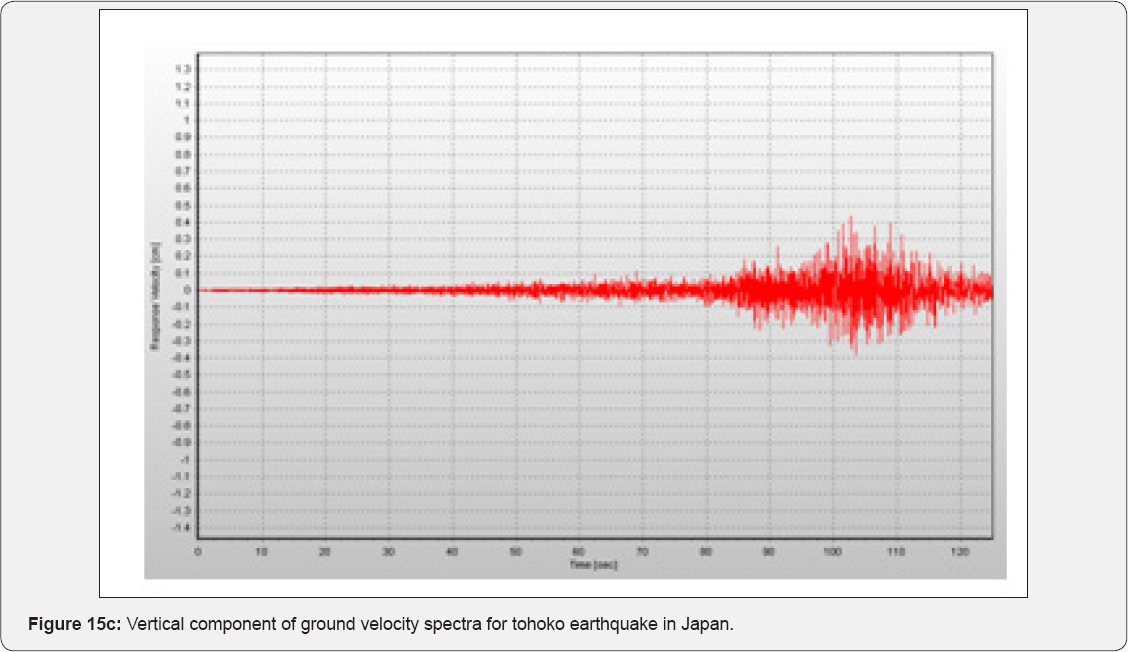
Empirical recordings have had a significant influence on the estimation of the maximum physical ground motions that can be possible. Peak ground acceleration is an important factor which needs to be investigated before testing devastation potentials that can result from earthquakes in rebuilding sites. One of the problems that deserve attention by seismologists is the occurrence of earthquakes where of the ground motion acceleration peak unexpectedly appears to be more than 1g (Figure 15-18). Valuable data on some earthquakes have been used by Strasser [6] to investigate the earthquakes' physical processes and their consequences.

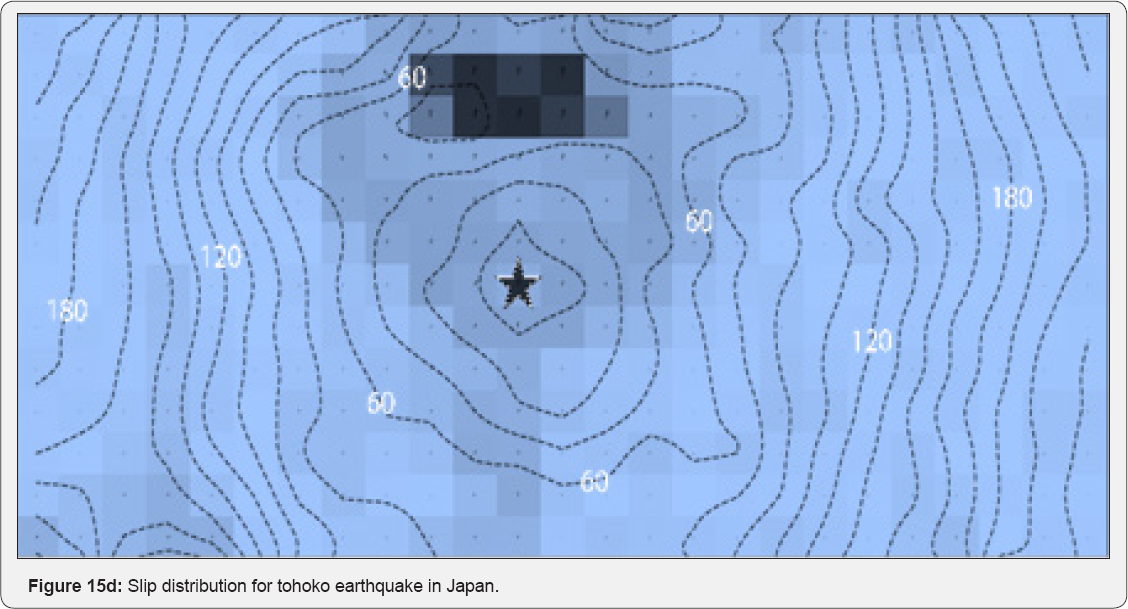
Figure 15a &b shows the acceleration and velocity traces of the horizontal components falling into this category for which the recordings were available. Spectra of pseudo-acceleration response, pertaining to damping by 5%, are also shown. All the examined traces are characterized by a very pronounced peak in the short-period (T<0.3s) range of the spectrum. The peak velocities that are associated with these recordings are less than 50cm/s. Slip distribution of focal mechanism for tohoko earthquake in Japan are shown in Figure 15c. The results of Gullo and Ercelebi's [2] research (2007) indicated that the fitting between the predicted PGA values by the networks and the observed ones yielded high correlation coefficients (R2). Furthermore, comparisons between the correlations by the ANN and the regression method showed that the ANN approach performed better than the regression method (Table 6). The developed ANN models can be used conservatively so as to establish a good understanding of the influence of input parameters for the PGA predictions.

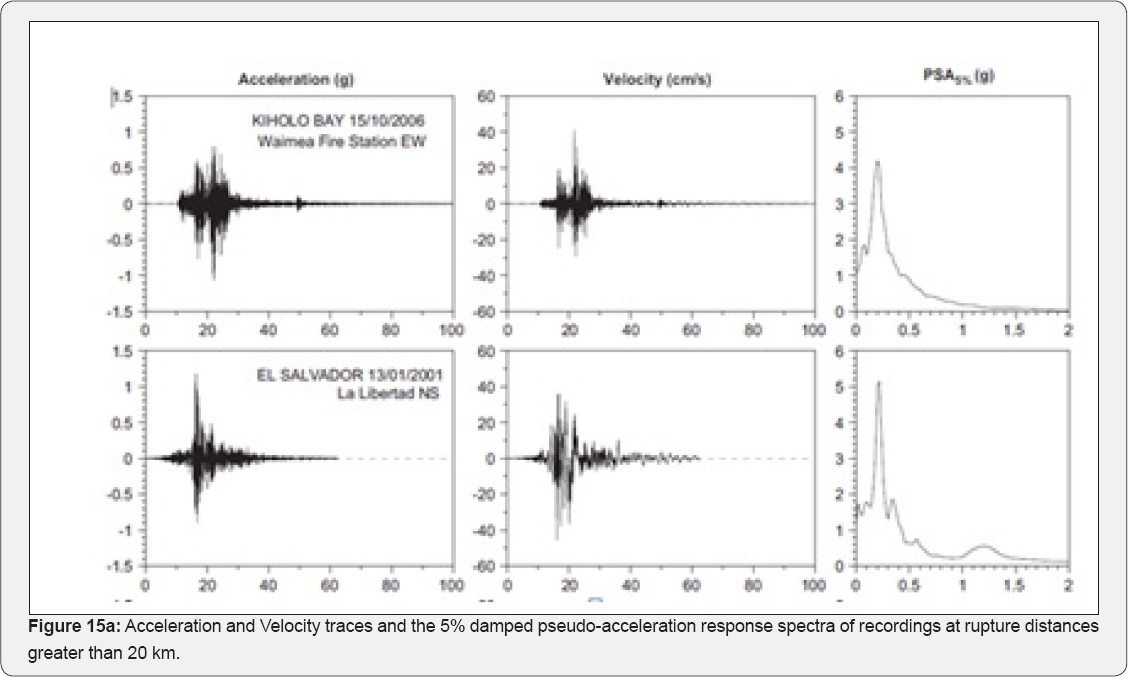
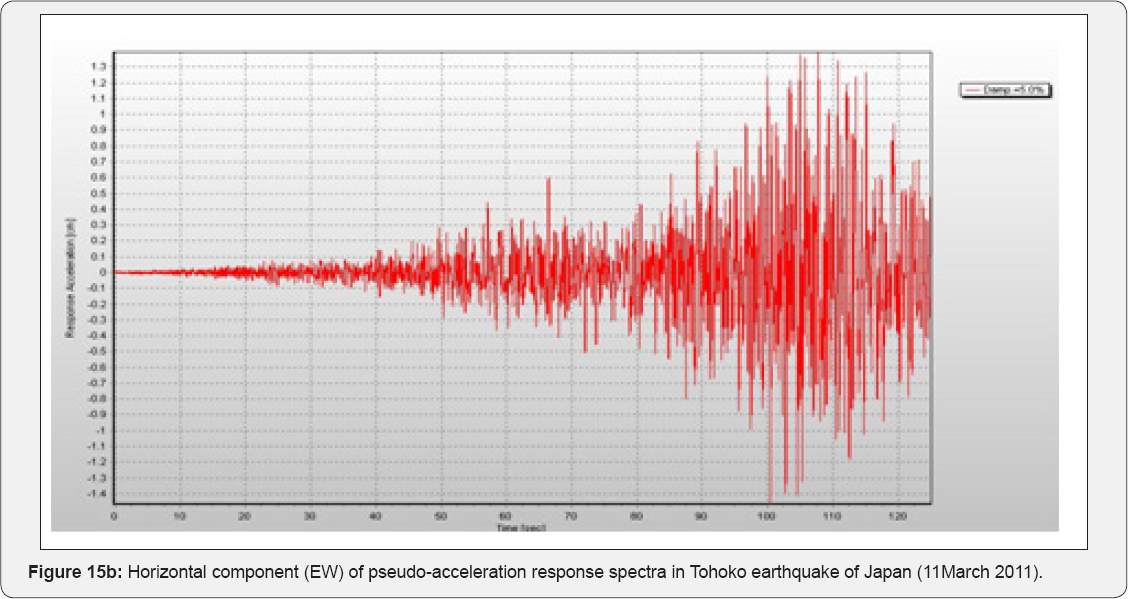
In Strasser and Bommer's [6] research, a dataset of recordings was examined. It was characterized by the recordings' large amplitudes of PGA (1g) (Figure 15). A number of physical processes have been proposed in the literature to explain these large ground motions, which are commonly divided into source, path and site related effects. While it is often a matter of convention whether these are considered to be predominantly linked to ground motion generation (source effects) or propagation (path and site effects), particularly in the nearsource region, it is important to distinguish between factors that are event-specific, station-specific and record-specific, in terms of implications for ground motion predictions and thus seismic hazard assessment. This is because only site-specific effects can be predicted for certain, in advance. In the present paper, the ANN algorithm indicated that the fitting between the predicted PGA values by the networks and the observed PGA values could yield high correlation coefficients of 0.851for PGA ( 3). Moreover, comparisons between the correlations obtained by the ANN and the regression method demonstrated that the ANN algorithm performed better than the regressions. The Levenberg-Marquart gradient method which we applied on the training algorithm contributed dominantly to fitting the results well.

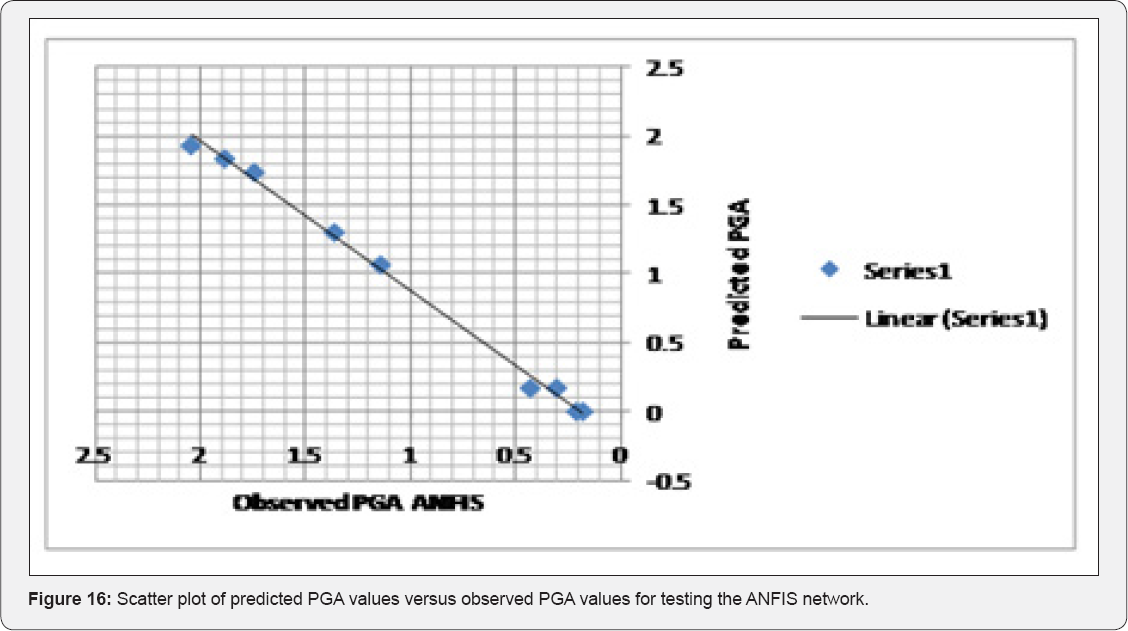
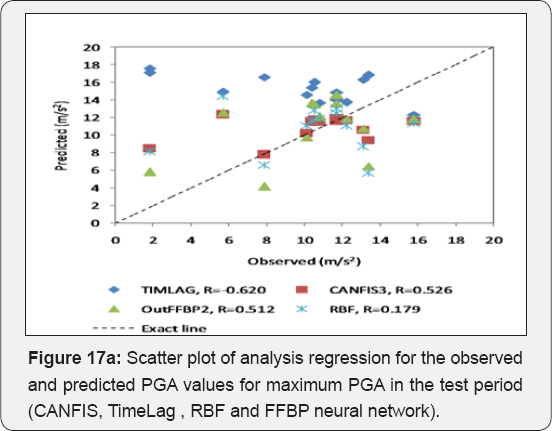
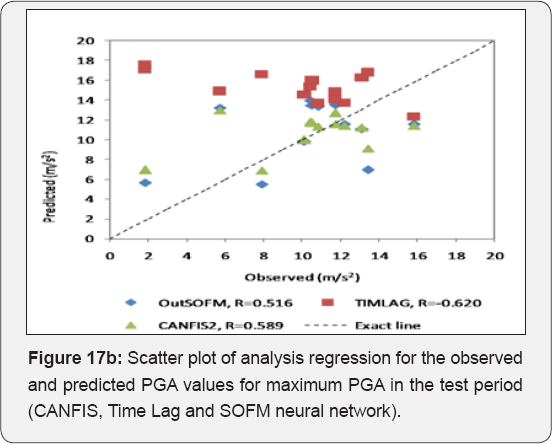
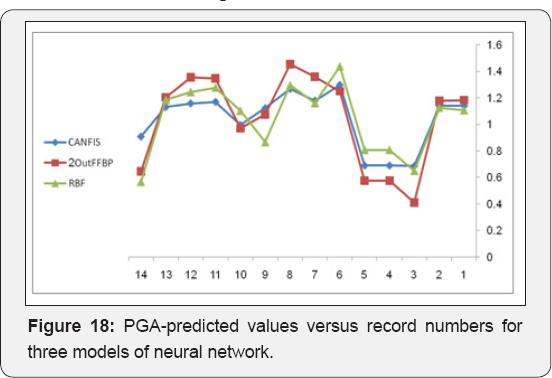
It had the potential to carry out training very quickly. Moreover, the network models developed in this paper offer new insights into attenuation studies for the purpose of estimating the PGA. In this study, ANFIS and FFBP models were developed to forecast the PGA in different regions of the world. The results of two models and the observed values were compared and evaluated based on their training and validation performance (Figures 2 & 4). The results demonstrated that ANFIS and FFBP models can be applied successfully to establish accurate and reliable PGA forecasting, when comparing the results of the two networks. It was observed that the value of R belonging to the FFBP models is high (0.78) (Figure 3). Moreover, the LSE values of the ANFIS model — which is 0.012 — were lower than that of the FFBP model (Table 4). Therefore, the ANFIS model could be more accurate than the FFBP model. However, a significant advantage is evident when predicting the PGAvia ANFIS, compared to the FFBP model (Figures 16 & 17). The simulations show that the ANFIS network is good for predicting maximum peak ground acceleration in some regions of the world. Finally, the minimum testing error- obtained for the ANFIS network- is 0.002 and the ultimate epoch error is 0.012 (Table 4). This conclusion shows that the ANFIS network can be suitable and useful for predicting values of peak ground acceleration for future earthquakes. PGA-predicted values versus record numbers for three neural networks are shown in Figure 18 & 19.

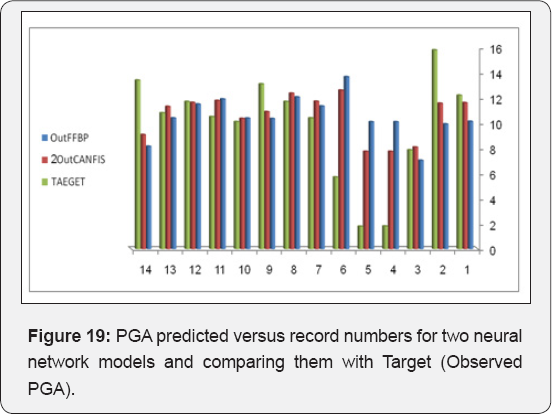
Conclusion

In this study, FFBP neural networks and ANFIS were trained so as to estimate peak ground acceleration in an area. The input variables in the ANN model were the magnitude, the rupture distance, the focal mechanism and site classification. The output was the PGA only. In the end, the minimum testing error was obtained for the ANFIS network, which equaled 0.002, and the mean square error for the FFBP neural network equaled 0.017. This conclusion shows that the ANFIS network can be suitable and useful in predicting peak ground acceleration for future earthquakes.

Acknowledgement

I am very grateful to the editors and anonymous reviewers, for their suggestions aimed at improving the quality of this manuscript. I also appreciate professors Strasser and Bommer for granting necessary data to this work.