Biostatistics and Biometrics Open Access Journal

Method of Obtaining Inter-Arrival Distribution between Two Consecutive Heart Attacks Using Palm Probability

Singh K¹,²* and Biswas S¹

¹Department of Statistics, Amity University, India

²Public Health Foundation of India, India

Submission: December 11, 2017; Published: April 18, 2018

*Corresponding author: Kalpana Singh, Amity institute of applied science (AIAS), Amity University, Noida, India, Tel: 9555428247; Email: nkalpanasingh@gmail.com

How to cite this article: Singh K, Biswas S. Method of Obtaining Inter-Arrival Distribution between Two Consecutive Heart Attacks Using Palm Probability. Biostat Biometrics Open Acc J. 2018; 6(1): 555679. DOI: 10.19080/BBOAJ.2018.06.555679

Abstract

An attempt has been made to obtain the inter-arrival times of two consecutive heart attacks by using the technique of Palm probability. The arrival rate of heart attacks is taken to be Poisson, which is assumed to vary individual to individual following gamma distribution leading to a dependent process. In this communication, a methodology has been used to estimate the consecutive failure time of heart attack with compound Poisson inputs weighted by gamma distribution based on hospital discharge data relating to heart failures.

Keywords: Palm probability; Waiting time distribution; Poisson process weighted by gamma distribution

Abbreviations: CHD: Coronary Heart Disease; EFFECT: Enhanced Feedback for Effective Cardiac Treatment

Introduction

Coronary heart disease (CHD) has been a leading cause of death worldwide; it is rapidly increasing in developed countries [1]. According to Jones L, et al. [2], American Heart Association National Center statistics 2010 approximately 60 % Americans had recurrent heart attacks. The incidence of CHD is 25-45% of all deaths worldwide, Shradha Chauhan, et al. [3], have reported 3% CHD prevalence in India. According to Mackay J, et al. [4], heart disease and stroke could become the leading causes of both disability and death worldwide by 2020. This paper attempts to develop a model for the estimation of the expected time between two consecutive heart failures with and without a number of concomitant comorbid illnesses (0, 1 or 2, 3 or more) using the concept of Palm probability. The present exercise between inter-arrival time of the two consecutive heart attacks on the assumption that heart attack occurs with Poisson rate X that varies from individual to individual following a two parameter gamma distribution (the best prior distribution of the conditional Poisson distribution ). It has been shown by Biswas & Pachal [5] and Biswas & Nair [6] the inter-arrival distribution becomes infinitely divisible with dependent increments. Palm probability represents the conditional probability of a finite number of events in a fixed interval of time given that an event has occurred at the beginning of the interval. Khinchin [7] has obtained the relationship between conditional and unconditional probability.Cox and Isham [8] developed the Palm probability model that deals with a series of problems on dependent processes.

This paper is methodological one that attempts to investigate the expected inter-arrival time between two consecutive heart attacks using data of David A, et al. [9] from the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) project conducted in Ontario, Canada to evaluate the effectiveness of public report cards in improving quality and outcomes of cardiac care. The EFFECT heart failure project was designed to be representative of the heart failure population of Ontario, and consisted of patients hospitalized with a diagnosis of heart failure across 86 Ontario acute care institutions from April 1, 1999, to March 31, 2000. Comorbidities at baseline included: hypertension, diabetes, family history of heart disease, hyperlipidemia, smoking currently, angina, CAD, CVA/ TIA, previous PTCA or stent, previous CABG, previous MI, atrial fibrillation, deep vein thrombosis, aortic valve disease, peripheral vascular disease, mitral valve disease, valve replaced or repaired, cardiomyopathy, alcohol consumption >2 drinks/ day, asthma, cancer, COPD, coronary pulmonary, cirrhosis, dementia/Alzheimer's disease, depression, GI ulcer disease, hepatitis, HIV/AIDS, hyperthyroid, nephritic syndrome, renal dialysis, renal artery stenosis, uncontrolled seizure, syncope in the past year. The objective of present study is,

a. To estimate the time between two consecutive heart attacks;

b. To analyze the effect of comorbid illnesses (no comorbidity, any 1 or 2, any 3 or more) on the expected time between the two consecutive heart attacks. The major advantage of the model is to predict the duration between two heart attacks.

Materials and Methods

Palm probability

Let the waiting time distribution of heart attack is denoted by the random variable X given with rate X, that varies from individual to individual as follows

Now, consider the non-overlapping renewal intervals say (0,S) and (S,t). The number of events in these two non-overlapping intervals is given by x(s) and x(t)-x(s).

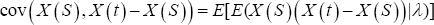
This shows that the number of heart attacks in any two non-overlapping renewal intervals are correlated.

Let (f>_r (t) be the conditional probability of r number of heart attacks in time (0, t) given that first heart attack has occurred at the beginning of the interval and n_r (t) be the unconditional probability of r heart attacks in (o, t); _r = 0, 1, 2,3.

Since f₁(t\.) is the conditional density function of waiting time of the first time given that an event has occurred at t=0. Proceeding in this way, differentiating equation (7)

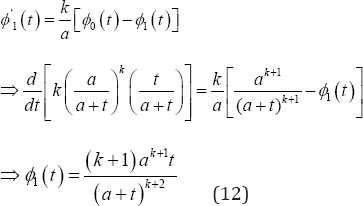
Similarly, f₂ (t |.) is the c.d.f of the waiting time distribution of the second arrival given that at t=0, the first arrival took place.

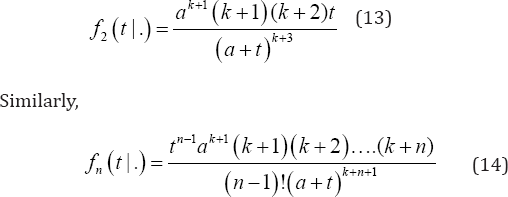
Equation (14) provides the distribution of the time between the first and nth arrival given that the first arrival occurred at t=0. Probability model of the waiting time distribution,()1thn+ of the heart attack given the arrival of first (r+1) heart attack at times t₁<t₂(r=0,1,..,n-1) The random time of the ()1thn+ heart attack which is fatal as nT (a random variable) and assuming Markovity in the sequence of ordered heart attacks, we have

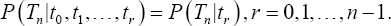
Let say, (r+1)^th order of heart attack r=(0,1,...,n-1) arrive with intensity and assuming that λ(0≥λ<∞)varies from individual to individual following the distribution as

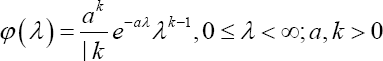
The Palm probability distribution of the waiting time of (_n+₁)^t* heart attack given that the (r +1) at t_ris given by

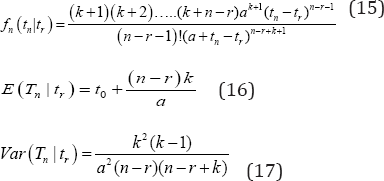
Results and Discussion

David A, et al. [9] has estimated the average life expectancy of patients with no comorbidity, any 1 or 2 comorbidities and any 3 or more comorbidities for male and female. The mean � SD of average life expectancy of heart failure patients of concomitant comorbid illnesses (0, 1 or 2, 3 or more) for male and female is given in Table1. We have estimated the shape and scale parameters of Pareto distribution by the method of moments from David A, et al. [9] and compare the same with obtained by Palm probability technique. It has been observed that the duration between heart attacks decreases as the number of comorbidity increases. The findings of this study showed that the Woman has more chance to get a second attack earlier than the men counterpart. Grover et al. [10] also found that the patients with sickness experiencing the second attack were higher [11].

Conclusion

In this problem the application of Palm probability is relevant because the consecutive arrivals of heart attack leads to an infinitely divisible distribution with dependent increments and the renewal structure is destroyed. Individuals with comorbidity, the first heart attack follows the second attack earlier than those individuals with no comorbidity. Further, research is needed to understand the relationship between the risk factors, an onset of consequent heart attacks, and lifestyle changes. Each additional comorbidity carries a progressively earlier risk of heart attack.