Biostatistics and Biometrics Open Access Journal

Cross-Sectional Data with a Common Shock and Generalized Method of Moments

Serguey Khovansky*

D'Amore-McKim School of Business, Northeastern University, USA

Submission: February 12, 2018; Published: March 28, 2018

*Corresponding author: Serguey Khovansky, D'Amore-McKim School of Business, Northeastern University, USA, Tel: 16173733616; Email: skk9e@virginia.edu

How to cite this article:Serguey K. Cross-Sectional Data with a Common Shock and Generalized Method of Moments. Biostat Biometrics Open Acc J. 2018; 5(5): 555674. DOI: 10.19080/BBOAJ.2018.05.555674

Abstract

This note outlines possible issues that arise when a common shock exists in such data which models are estimated using Generalized Method of Moments. It provides a theoretical foundation of the issue, an approach to its solution and a reference to an empirical application.

Keywords: Generalized method of moments; Common data shock; Single cross-section of data

Introduction

Cross-sectional data generated at the same point in time may be affected by an exogenous stochastic common shock that influences all data units, perhaps, to a varying extent. Such data generating processes can be found in environmental, ecological and agricultural sciences as well as in economics and finance. For example, storms, floods, droughts, and earthquakes impact the development of biological systems consisting of many individual species. Shocks in the energy markets bring about changes in the production costs of firms across many industries. Interest rate shocks may be responsible for the consumption and savings decisions of many households. Technological shocks affect the evolution of ecosphere. Legal and political shocks may change the perspectives of business firms.

From the econometric point of view, a key consequence of a stochastic common shock shared by all population units is the loss of independence among individual observations, even at the asymptotic level. As a result, the standard versions of the laws of large numbers and central limit theorems become inapplicable. Consequently, the common shock makes inappropriate the regular estimation methods, e.g. GMM (Generalized Method of Moments). This happens, for example, because the large-sample properties of the estimators become dependent on the common shock and lose consistency. To be more precise, the classical GMM consistency proof of Newey & McFadden [5], is valid only for such data where dependence declines as the "distance" between them increases, i.e. even when a shock is present it should not be shared by all population units for the proof to be applicable. Thus, it is very plausible that statistical models based on GMM that do not take the common shock into account (when it indeed exists) end up with inconsistent estimates.

How to address the presence of a common shock shared by all population units? It is only intuitive that the shock must be included in the estimating procedure as a conditioned variable. As is well known, under certain circumstances unconditionally dependent events might be conditionally independent. To be more specific: If two events A and B are dependent, then Pr (A ∩ B) ≠ Pr (B) Pr (A).However, it is possible that there exists an event S with Pr(S > 0) such that conditioning on it the events A and B become independent, i.e. Pr (A ∩ B) = Pr (B) Pr (A).

Generally, theoretical and empirical research about the effect of stochastic common shocks on properties of cross-sectional estimators has received limited attention in the literature, especially in the case of GMM estimators. To a certain extent, this negligence can be explained by computational difficulties associated with estimation procedures that account for the presence of such a shock. Conley [1] examines cross-sectional GMM estimation under a version of a common shock, that is not shared by all population units. Andrews [2] looks at properties of ordinary least squares (OLS) estimators in a setting where common shocks may be present. Andrews [3] also studies properties of instrumental variable (IV) estimators and proposes a set of regularity conditions under which GMM estimators are consistent. Khovansky & Zhylyevskyy [4] suggest a modified GMM estimator and provide conditions under which these estimators are consistent. To implement the proposed GMM estimation approach, a realization of the stochastic common shock must be observed. The essential feature of the method is that it uses conditional rather than unconditional statistical moments. The conditioning is implemented on the sigma-field σX₀) generated by a common shock X₀ i.e. the GMM objective function is

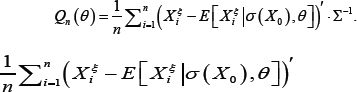
with the estimate given by 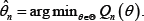The variable X_o and the variables x₁, x₂,,... are all stochastic. Also, the realization of the random variableX₁, X₂,...,...X_n. is revealed simultaneously with the realizations of the other random variables. It should be emphasized that in this case the textbook consistency proof of Newey & McFadden [5] is not valid because the GMM objective function Q_(θ) converges to a stochastic, rather than deterministic, function. By employing this approach, we can estimate some parameters of a time-series model using currently available cross-sectional data instead of historical time-series. The estimates obtained in this way would reflect the most recent data rather than the past history. Such a course may be appropriate when historical data are irrelevant for the description of the current empirical situation.

Khovansky & Zhylyevskyy [6] give a concrete empirical application which illustrates the use of the proposed estimator. It explores a financial market model comprising a cross-section of stocks and a market portfolio index. In the model, the common shock is represented by the price dynamics of the market index (which reflects the systematic risk) that induces cross-sectional dependence among individual stock returns. In addition to that, the individual stock returns are affected by stock-specific stochastic, i.e. idiosyncratic, risks. An additional important detail is in order. The effect of a common shock on each specific unit may depend on that unit, i.e. vary across the units. To model this heterogeneity appropriately, we might design this dependence as a random variable with some distribution and then, as in the case of GMM, integrate it out by applying the law of iterated expectation.

Future work

Aside from such conventional questions as asymptotic distribution, the Wald test and overidentifying restrictions test in the presence of a common shock, there is also an interest in the question of when and specifically how we should take a common shock into account when dealing with regressions (e.g. in order to obtain consistent estimates). The issues of weak identification, small sample properties, the simulated method of moments and indirect inference are other possible research extensions.