Biostatistics and Biometrics Open Access Journal

Analysis of Biological and Biomedical Data with Circular Statistics

Domien Craens and Christophe Ley*

Department of Applied Mathematics, Computer Science and Statistics, Ghent University, Belgium

Submission: February 26, 2018; Published: March 12, 2018

*Corresponding author: Christophe Ley, Department of Applied Mathematics, Ghent University, Krijgslaan 281, S9, Campus Sterre, B-9000 Gent, Belgium, Tel: +32 9 264 49 08; Email: christophe.ley@ugent.be

How to cite this article:Domien Craens, Christophe L. Analysis of Biological and Biomedical Data with Circular Statistics. Biostat Biometrics Open Acc J. 2018; 5(5): 555671. DOI: 10.19080/BBOAJ.2018.05.555671

Abstract

In this note we will show how circular statistics allow a more accurate and better analysis of several biological and biomedical data sets for which the classical statistical tools may lead to wrong conclusions.

Keywords: Circular data; Directional statistics; von Mises distribution; Structural bioinformatics

Opinion

Several biological and biomedical data sets should by nature be considered as observations lying on the unit circle instead of on a real interval. Studying data on the unit circle requires special care, as the classical statistical concepts no longer hold for such data. Consider for instance the arrival times of patients at a hospital's emergency room or secretion times of certain human hormones. One would naively think of representing histograms of these data on a [0h00; 23h59] interval. To see the first and foremost problem of this approach, consider the problem of analyzing and modeling the secretion times of the hormone melatoninl for patients with sleep disorders. An obvious statistic of interest would be the average time point of melatonin secretion. Say for the sake of simplicity we observed two secretion times, 23h55 and 0h05. Intuitively it is obvious that the time of secretion is concentrated around midnight (0h00), however simply calculating the average time would yield noon (12h00). The reason for this problem lies at the artificial choice of cutting the cycle of a day at midnight (0h00). If we choose for example noon as cut point and represent the data on a [-12h00; 11h59] interval (the times in the interval [12h00; 23h59] are now denoted by the interval [-12h00;-0h01]), our two observations correspond to -0h05 and 0h05 and the average gives the correct value 0h00.

With more data and more spread out data, the art of carefully choosing the cut point will no longer be possible, implying that the traditional mean can no longer be used to calculate an average. This issue can be naturally solved by plotting the data on a unit circle. This allows the natural continuity between any two subsequent times and makes no difference between, say, the passage from 11h15 to 11h16 and the passage from 23h59 to 0h00. The circular mean is then obtained as follows. Suppose we rescale the data to angles θ_i in[0,2π] radians. These correspond to the points (cos (θ_i),sin (θ_i)) on the unit circle. The two-dimensional mean point on the circle corresponds to 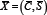, where 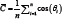and 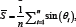, leading to the average angle 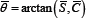. The latter mean value solves the above-mentioned problems.

Since such a basic concept as the average requires already special care for this type of data, the reader can imagine that all statistical concepts, ranging from descriptive statistics to hypothesis tests, need to be revisited for this type of data. Devising appropriate statistical methods to deal with circular data has grown into an entire research field called circular statistics, and is part of the more general research stream of directional statistics [1]. We have described examples of datasets where the circle was used to represent times. Obviously, it can also be perceived as a compass measuring directions as, e.g., in the study of animal orientation. Probability distributions are the building blocks of statistical methods, and many research efforts, especially in recent years, have been devoted to the study of circular probability distributions. The simplest one is the uniform distribution on the circle with constant density function 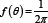for all angles θ. It is easy to see that this corresponds to the case where every angle is equally likely.

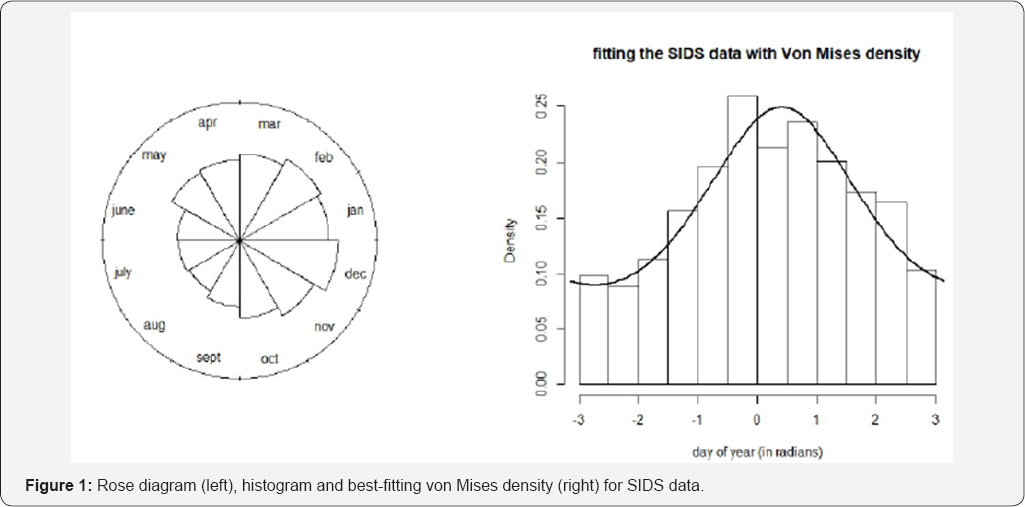
The most notorious probability distribution in circular statistics is undoubtedly the von Mises distribution. It is often viewed as the equivalent of the normal distribution for circular data and its density reads , where μ ∈ [0,2π) is the central location (or mean), the parameter Eq. 1 controls the dispersion of the distribution around π and I_o(^k) is a normalizing constant. We will briefly illustrate the use of this distribution on data about the Sudden Infant Death Syndrome (SIDS) studied in Mooney et al. [2]. The authors investigated monthly totals of SIDS deaths in England, Wales, Scotland and Northern Ireland for the years 1983-1998, a period including the "Back to Sleep" campaign from the early 1990s that successfully led to a reduction in SIDS deaths. Since there does not exist a natural cut point in the twelve months of a year, these data are by nature circular. We show in Figure 1 the distribution of deaths for the year 1986 both as a rose diagram (a circular histogram) as well as under the form of a more classical histogram, to which we have superimposed the best-fitting von Mises distribution (whose parameters have been estimated by means of maximum likelihood estimation). Mooney et al. [2] have analyzed the evolution of SIDS deaths over the years and investigated whether mixtures of von Mises distributions allow to discover patterns in SIDS mortality rates.

We conclude by providing the reader with an outlook on a hot research topic involving circular statistics, namely the protein structure prediction problem from structural bioinformatics. Predicting the correct three-dimensional structure of a protein given its one-dimensional protein sequence is seen as a holy grail problem. A protein consists of a sequence of amino acids, which essentially defines its three-dimensional shape and dynamic behaviour. Understanding the protein structure at local level represents a key component, and this local structure is adequately described using pairs of dihedral angles per amino acid. In recent years, researchers have made important progresses in this domain by recognizing that these pairs of angles are best described as data on the product space of two circles (a torus) and using the appropriate statistical techniques[3]. Improving further the state-of-the-art statistical tools is very likely to lead to significant further progress in this passionating problem. We hope to have convinced the reader of the usefulness and need to view appropriate biomedical and biological data as observations on the circle. For further reading, we refer the reader to the by now classical book Jammalamadaka & SenGupta[4],as well as to the recent monographs Pewsey et al. [5], focusing on using the software R for dealing with circular data, and Ley & Verdebout [6] which provides an up-to-date account on modern methodologies in the field of directional statistics.