Estimating and Testing the Effect of Delayed Marriage on Fertility
Uzuke CA* and Oyeka ICA
Department of Statistics, Nnamdi Azikiwe University, Awka
Submission: November 29, 2017; Published: February 22, 2018
*Corresponding author: Uzuke CA, Department of Statistics, Nnamdi Azikiwe University, Awka, Nigeria; Email: ca.uzuke@unizik.edu.ng
How to cite this article: Uzuke CA, Oyeka ICA. Estimating and Testing the Effect of Delayed Marriage on Fertility. Biostat Biometrics Open Acc J. 2018; 5(2): 555656. DOI: 10.19080/BBOAJ.2018.05.555656
Abstract
A statistical model which can be used to estimate the loss of fertility due to delayed marriage after the age at menarche was proposed. This model made use of a cohort of women who had their menarche at age 13 years. The expected number of years of spinsterhood was also estimated
as e(x). The result showed that a spinster who had her menarche at age 13 years and delayed her marriage on the average 12 years is going to loose on the average 2 children.
Keywords:Menarche; Menopause; Delayed marriage; Lost fertility; Probability distribution
Introduction
For purposes of child bearing, menarche is the initiation of a woman's ability to conceive and menopause, the cessation of this ability are two events that are of great importance biologically in a woman's life. If fertility is closely associated with effective cohabitation indicated by regular marriage, then delayed marriage is likely to strongly impinge on fertility. In this paper we propose to develop a statistical model that would enable the estimation of the effect of delayed marriage on fertility. Martin [1] observed that in USA, one of the stylized facts from the past thirty years has been the declining rate of first births before age 30 for all women and the increase rate of first births after age 30 among women with four-year college degrees. What are some of the factors behind women’s decision to postpone their childbearing? Waldfogel [2] hypothesize that the wage difference often observed between like-educated mothers and non-mothers may be affected by the postponement of childbearing until after careers are fully established.
Higher fertility level had been reported for women who married in their teens and an increase in the average age at marriage had been reported to have adverse effect on high fertility. Direct effects of women marrying in their teens include too many teen pregnancies which could have negative effect on the health of women and a longer fertility span for women resulting in raised average number of children born by women [3]. In much of the developing world, adolescent and child marriage continues to be a strong social norm, particularly for girls. Early female marriage is associated with a number of poor social and physical outcomes for young women and their offspring. On average, girls who marry as adolescents attain lower schooling, have lower social status in their husbands' families, report less reproductive control, and suffer higher rates of maternal mortality and domestic violence. In addition, these individual outcomes suggest a number of larger social consequences of early marriage, including higher population growth, more rapid spread of disease, and a higher incidence of orphans [4].
As a result of these patterns, governments in developing countries face increasing pressure to eradicate the practice with legal sanctions against parents who marry daughters before a standard age of consent. Proponents of age of consent laws argue that forcing parents to delay marriage will increase female schooling attainment and reproductive control, and decrease incidence of domestic violence. On account of these arguments, social programs increasingly contain program rules designed to discourage the practice. For instance, a prominent microfinance program in India excludes parents who marry daughters before 17, and national education vouchers in Bangladesh exclude married girls. However, while statistics indicate that women who marry young fare worse, it is difficult to assess the extent to which these outcomes are driven by the timing of marriage as opposed to common factors related to poverty and traditional gender views that also hinder female advancement. Given that child marriage is most common in impoverished and culturally traditional settings, the observation that women who married young have on average less education clearly does not imply that forcing girls to postpone wedlock would improve their outcomes.
The genetic component of age of menarche may imply that women with later onset of puberty have the additional advantage of having mothers that also experienced later marriage [5]. In this sense, the benefits of late marriage may be transmitted through intergenerational linkages other than biology. If later marriage leads to higher schooling attainment, families in which this biological trait is prevalent across generations may be those with persistently higher investment in girls [6]. As explained by Begum [7], "In Bangladeshi society a teenage daughter reaching menstruation becomes a burden for many parents because preservation of her virginity is the greatest concern for a bride. As a result parents like to get their daughters married as early as possible. Why have these dramatic changes in fertility patterns occurred? Clearly, a number of factors have taken place simultaneously. The factors include the previously mentioned increase in female employment, particularly for mothers; rising education levels of all women; an opening up of professional, career occupations once dominated by men; and changing social attitudes, to name the most important. Most relevantly, the trends with regard to age at first birth and mother's education are linked.
The proposed method
Let n(0) be the initial size of a cohort of single girls who reach their menarche during the year drawn from a certain population. Let X be a random variable representing the length of time a randomly selected individual from this post-menarche cohort of girls remains a spinster before first marriage. Then X may be interpreted as the post-menarche 'age' before first marriage of the randomly selected single girl from the cohort. That is X is the time duration from menarche to first marriage. We assume that this cohort of girls is subject to and would experience the schedule of age specific fertility rate, M(x) at age x currently prevailing in the population from which they are drawn. It is also here assumed that child bearing outside marriage in this population is negligible and that pregnancy and child bearing naturally follow immediately after marriage. It is further assumed that no woman in the population dies before first marriage. These assumptions are clearly rather restrictive but they nevertheless would enable the estimation of fertility, even if only the gross rates.
If an appropriate age dependent marriage life table for the population is available, then the age specific fertility rates may be applied to the life table age specific marriage rates, and sum to obtain the required gross fertility rate of the population. However in the absence of an adequate life table, it is possible to hypothesize and fit a statistical probability distribution model to X , the length of time between spinster's menarche and first marriage that is a spinster’s post-menarche age before first marriage. If a goodness of fit test shows that the model is adequate then such a distribution may be used to estimate the desired fertility rates. This approach is adopted in the sequel.
Suppose x follows a continuous probability distribution model with probability distribution function f (x), for 0 < x < co. Note that 0 the lowest possible value assumed by X coincides with a , the lowest age at menarche in a population, while the width of the range of X coincides with the width of the child bearing span that is o = p — a where p is the highest age in years at menopause. In practical applications and without loss of generality, we can assume that a = 15years and P = 15years, so that o = 35years . It can be reasonably assumed that child bearing is not possible outside the age interval (a,p) years. Hence marriage outside this age interval, that is before menarche or after menopause does not importantly affect fertility and may for all practical purposes be ignored. Therefore by implication the highest value x can assume is as specified o = P — a years and the lowest value is 0. Under the above specifications the probability that a randomly selected postmenarche single woman marries before time x , that is spends less than x years as a spinster in the cohort of single women is:
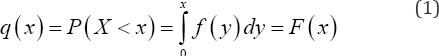
Hence, the number of single women removed from the cohort up to time x as a result of marriage is:
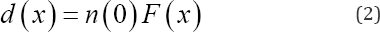
The probability that a randomly selected post-menarche single woman from the cohort marries between time x and time z , that is in the post-menarche age interval (x, z) is;
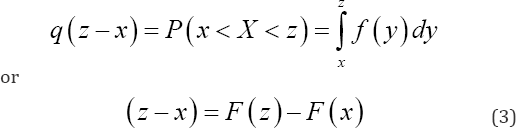
The number of single women expected to be removed from the cohort as a result of marriage in the time interval (x — z) is
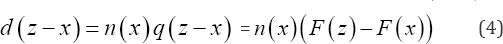
Where, n(x) is the number of single women in the cohort
at the beginning of the interval (x, z). The number of postmenarche women in the cohort expected to still be single at the end of the interval (x, z), and hence at the beginning of the immediately succeeding time interval is
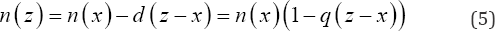
However, since emphasis is on delayed marriage, of greater interest perhaps is the number of post-menarche single women who fail to marry at age X but marry at a later age z , that is who postpone their marriage from time x to time z perhaps to complete schooling. Now the probability that a randomly selected post-menarche single woman from the cohort does not marry before time x but marries before time z , that is remain single beyond age x, but marries before age z , z > x is
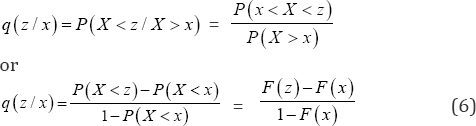
The corresponding number of single girls removed from the An unbiased estimator of this population mean d is the
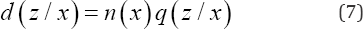
Where, n(x, z) is the equivalent number in the immediately preceding time interval? Hence the number of women in the cohort who remain unmarried at the end of the time interval(x z)is
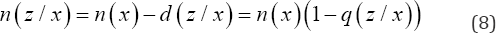
To establish lost fertility we note that the number of person- years, the n(z / x) post menarche women who postponed marriage, that is do not marry before age x but marry before age z , spend in the age interval (x, z) as spinster before first marriage is z L (x ) = J n (z / y)dy(9) Hence, the overall or total fertility loss by the post-menarche cohort of single women that is those who delay marriage (who do not marry) before time x but marry before time z is
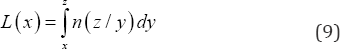
Hence, the average fertility loss by the post-menarche cohort of single women before their first marriage which may be termed lost fertility due to delayed marriage after menarche is
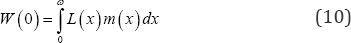
Now replacing f(y) in equation (1) with its value in (12) integrating and evaluating gives the probability that a randomly
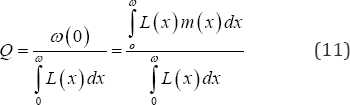
selected post-menarche single woman spends less than x years as a spinster before first marriage, that is marries before time
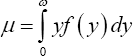
An unbiased estimator of this population mean ƒÊ is the sample mean x . If x can be obtained from the observations on the post menarche length of stay before marriage of an adequate sample of single women. It may be used to calculate any parameter if unknown of a hypothesised probability distribution for x and then used in estimating the rates and numbers in equation (1-10).
A hypothesised probability distribution for x
Suppose on the basis of some a priori knowledge, it is believed that x , the length of time a randomly selected post menarche single woman spends in spinsterhood before first marriage follows the continuous probability distribution with probability distribution function
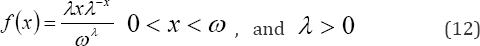
Now replacing ()yf in equation (1) with its value in (12) integrating and evaluating gives the probability that a randomly selected post-menarche single woman spends less than x years as a spinster before first marriage, that is marries before time x as
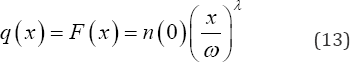
The corresponding number of single women from the cohort expected to be in this category, that is married before time x and hence removed from the cohort of single women is
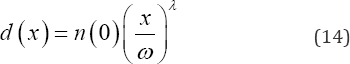
The probability that a randomly selected post-menarche single women from the cohort marries in the age interval ()zx, is obtained from equation (3) as
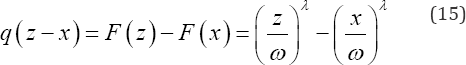
From equation (14) we have that the number of post menarche single women expected to marry in the time interval ()zx, and hence be removed from the cohort of single women is
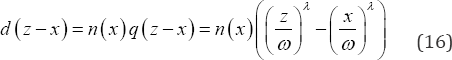
From equation (5) we have that the number of post-menarche women in the cohort expected to still be single at the end of the interval ()zx, and hence at the beginning of the immediately succeeding time interval is
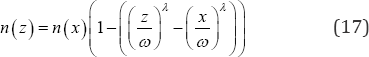
Similarly we have from equation (6) that the probability that a randomly selected post-menarche single woman is not married before age x but marries before age z is
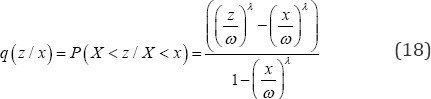
The corresponding number of post-menarche single women in this category equation(7)is
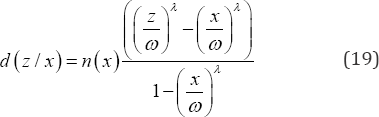
The corresponding number of post menarche single women still remaining to be married is therefore
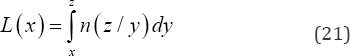
The number of person years post-menarche single women who delayed marriage, that is who are not married before time x but marry before time z , spend in the time interval ()zx, before first marriage is obtained using equation (20) in equation (19) as
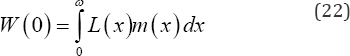
Where, ()yzn/ is given by equation (20).
Hence the overall or total fertility loss by the post-menarche cohort of single women who delay marriage that is who do not marry before time x but marry before time z is
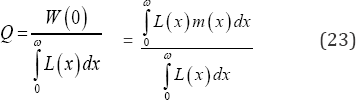
Hence the average fertility loss due to delayed marriage by this cohort of women is obtained by using equation (22) in equation (11), specifically as

Finally the length of time or mean number of years post-menarche single women spend in spinsterhood before first marriage is obtained using equation (12) in equation (11) after integration and simplification as

If an appropriate sample data are calculation of the sample mean x which as noted above is an unbiased estimator of the population mean ì, then x may be set equal to ì. which would now enable the estimation of any unknown parameter ë of the hypothesised probability distribution of x, obtaining the estimate as
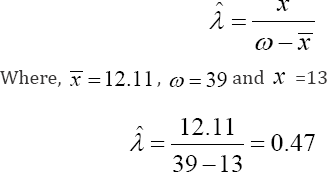
This estimated value of ë. may now be used in equations (13)-(24) to obtain required rates.
Illustrative example
In the study on age at first marriage and fertility among female civil servants in Anambra state, the following data obtained on the age at menarche and age at first marriage and were presented in Table 1 [8]. This table was used to illustrate the effect of delayed marriage on fertility as follows. From equation (25)
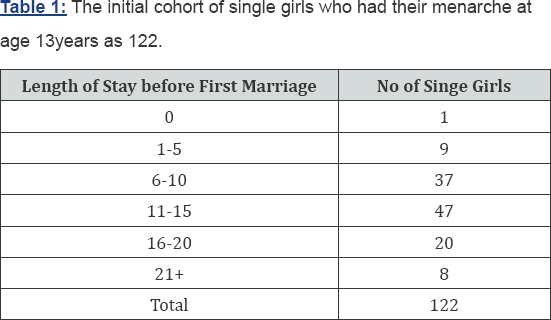

This estimated value of μ may now be used in equations (13).23) to obtain the required rates and presented in Table 2. Hence from Table 2, This implies that the loss of birth per woman due to delayed age at marriage is approximately 2 children [9].
Summary and Conclusion
We have here presented a statistical model which can be used to estimate the loss of fertility due to delayed marriage after the age at menarche. This model made use of a cohort of women who had their menarche at age 13 years. Also, the expected number of years of spinsterhood was estimated as . The result showed that a spinster who had her menarche at age 13 years and delayed her marriage on the average 12 years is going to lose on the average 2 children.
References
- Martin SP (2000) Diverging Fertility Among U.S. Women Who Delay Childbearing Past Age 30. Demography 37(4): 523-533.
- Waldfogel Jane (1998) Understanding the Family Gap in Pay for Women with Children. The Journal of Economic Perspectives 12(1): 137-156.
- Akpan OM, Ikpotokin O (2012) Modeling the Determinants of Fertility among Women of Childbearing Age in Nigeria: Analysis Using Generalized Linear Modeling Approach International Journal of Humanities and Social Science 2(18): 167-176.
- Abioye-Kuteyi EA, Ojofeitimi EO, Aina OI, Kio F, Aluko Y, et al. (1997) The Influence of socioeconomic and nutritional status on menarche in Nigerian school girls. Nutr Health 11(3): 185-195.
- Damon A, Damon ST, Reed RB, Valadian I (1969) Age at menarche of mothers and daughters, with a note on accuracy of recall. Hum Biol 4(2): 160-175.
- Haq MN (1984) Age at menarche and the related issue: a pilot study on urban school girls. J Youth Adolesc 13(6): 559-567.
- Begum Lutfa (2003) Meaning Given to Adolescents’ Reproductive Health in Bangladesh. Journal of Population 9: 81-103.
- Ezesuokwu CA (2000) Age at First Marriage and Fertility Among Female Civil Servants in Anambra State Nigeria for the year 1998, Unpublished MSc Thesis Submitted to Department of Statistics Nnamdi, Azikiwe University Awka, Nigeria
- Ekele BA, Udoeyop EU, Otubu JA (1996) Age at menarche amongst school girls in a high altitude Nigerian town. West Afr J Med 15(3): 170-172.






























