Biostatistics and Biometrics Open Access Journal

Review Article

Be Wary of Using Poisson Regression to Estimate Risk and Relative Risk

Zhu C¹, Blizzard L¹, Stankovich J², Wills K¹ and Hosmer DW³

¹Menzies Institute for Medical Research, University of Tasmania, Australia

²School of Medicine of Tasmania, Australia

³Department of Public Health, University of Massachusetts,USA

Submission: November 17, 2017; Published: February 09, 2018

*Corresponding author: Leigh Blizzard, Professor, Senior Member and Principal Researcher Menzies Institute for Medical Research, University of Tasmania, Private Bag 23, Hobart TAS 7001, Tel: 61 3 6226-7719, Fax: 61-3-6226-7704, Email: Leigh.Blizzard@utas.edu.au

How to cite this article: Zhu C, Blizzard L, Stankovich J, Wills K, Hosmer DW. Be Wary of Using Poisson Regression to Estimate Risk and Relative Risk. Biostat Biometrics Open Acc J. 2018; 4(5): 555649. DOI:10.19080/BBOAJ.2018.04.555649

Abstract

Fitting a log binomial model to binary outcome data makes it possible to estimate risk and relative risk for follow-up data, and prevalence and prevalence ratios for cross-sectional data. However, the fitting algorithm may fail to converge when the maximum likelihood solution is on the boundary of the allowable parameter space. Some authorities recommend switching to Poisson regression with robust standard errors to approximate the coefficients of the log binomial model in those circumstances. This solves the problem of non-convergence, but results in errors in the coefficient estimates that may be substantial particularly when the maximum fitted value is large. The paradox is that the circumstances in which the modified Poisson approach is needed to overcome estimation problems are the same circumstances when the error in using it is greatest. We recommend that practitioners should be wary of using modified Poisson regression to approximate risk and relative risk.

Keywords: Relative risk; Log binomial model; Poisson regression; Boundary point

Abbreviations: GLM: Generalized Linear Model; LBM: Log Binomial Model; ML: Maximum Likelihood

Introduction

Direct estimation of risk and relative risk for prospective studies requires the fitting of a generalized linear model (GLM) with a binomial error distribution and logarithmic link function. This is the log binomial model (LBM). It provides estimates of probabilities and conditional probabilities that are directly interpretable and are preferred as measures of occurrence and association [1]. An added benefit is that the model provides interpretable estimates of prevalence and prevalence ratios for cross-sectional studies.

The drawback of the LBM is that the logarithmic link function maps the probability of the event onto the negative real line. This imposes bounds on the allowable parameter space for the model coefficients. Estimation subject to boundedness is problematic, but standard methods for fitting GLMs may fail to converge to the maximum likelihood (ML) estimates for a LBM if the fitted probabilities are allowed to equal or exceed unity. Even if the iterations converge and the approximate solution is reasonably accurate, there will be difficulties interpreting and applying the fitted values if one or more of them exceeds unity.

There are several work-around methods to approximate the solution of a LBM and circumvent the problems inherent in its estimation. Other than substituting estimates from a logistic regression model, the modified Poisson regression method has gained the most traction [2]. This method involves fitting a GLM with a Poisson error distribution and logarithmic link [3], and using the sandwich estimator to obtain variance estimates that are robust to the error misspecification [4]. Carter et al. [5] showed that the coefficient estimates from a Poisson regression model consistently estimate the coefficients from the LBM, and that the information sandwich estimator of the covariance matrix of the Poisson regression fit is a consistent estimator of the covariance matrix of estimated coefficients from a log binomial fit.

This approach requires no data modification and can be easily performed using widely available software. It seemingly resolves the convergence issues because Poisson regression maps the logarithm of the count of events to the entire real line. Thus, estimation can proceed even if the linear predictor is nonnegative. This means that the resulting coefficient estimates may yield fitted values for the LBM that are inadmissible as probabilities because they exceed unity. Some authors have suggested that these can safely be ignored [6]. However, the approximate solution may be subject to considerable error. Our eyes to this were opened by example data in a recent paper by Williamson et al. [2] exploring sources of failed convergence of the LBM (Table 1). The authors attempt to fit the single covariate LBM

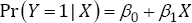
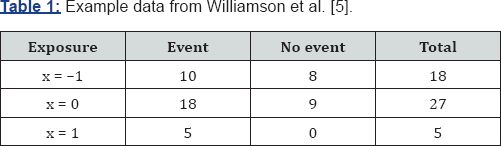
Where, Y is a binary (0/1) outcome indicator with Y = 1 denoting an event, and X is a covariate taking values x = {-1,0,1}. The maximum likelihood (ML) solution for a LBM model of these data is 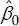=-0.344616 and 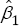= 0.344616. This solution is on a boundary β_o + β₁ = 1 of the allowable parameter space. The authors estimate the LBM with SAS (version 9.2), R (version 2.12.1), Stata (version 11.1) and SPSS (version 19) and report that only SAS is successful in finding the ML solution, though a warning is given in the SAS output that the convergence is questionable because the solution appears to be on the boundary.

In these circumstances, the analyst might follow well- intentioned advice to fit a modified Poisson model [5,7]. If so, the coefficient estimates 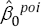=-0.3596015 and 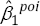= 0.2713417 would be obtained. The percent error in the slope estimate 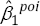is a staggering 21.3%. In fitting a modified Poisson model with four categorical covariates, Marschner & Gillett [8] also found errors greater than 20% for some categories of the risk factors. To investigate, we simulated data from a LBM with a single continuous covariate and for a range of values of the parameters β_o and β₁ Values of the continuous covariate were drawn at random from a distribution uniform on the range

A value at the top end of that range would lie on the boundary of the parameter space. For each observation i = 1,2,...n, values of Y_i = 1 were assigned to the outcome indicator if a random drawing from a distribution uniform on was less than the design value π(x₁) = exp(β_o + β_lx_i) of the LBM probability. Datasets of size n = 500 were chosen as representative of many encountered in practice, and 10,000 replications were drawn for each setting. Table 2 shows percentiles of absolute percent error in the Poisson estimate 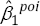of the LBM slope parameter relative to the ML estimate pp. The results were similar irrespective of the design values β₀ and β₁ For brevity, they are given for the setting β_o = ln (0.3) and β₁ = ln(1.5) only.

There was a moderate correlation (r = 0.48) between absolute percent error and the maximum fitted value from the modified Poisson model. This deterioration in the performance of the modified Poisson model with the size of the fitted value has been identified previously [8]. Relative error was at least 10% on 7.6 percent of simulations overall, on 11.3 percent of simulations when the ML solution was on the boundary, on 14.3 percent of simulations when a Poisson fitted value exceeded unity, and on 15.6 percent of simulations when the ML solution was on the boundary and additionally the Poisson fitted value exceeded unity.

Conclusion

We recommend that practitioners be wary of using the modified Poisson approach to estimate a LBM. Whilst errors greater than 20% may be a rarity, the estimates are subject to substantial bias. In the context of confounding, one authority has nominated 10% as the threshold for bias than cannot be ignored [9]. Based on that standard, the modified Poisson method failed on one-in-nine occasions when the ML solution was on the boundary, and on almost one-in-six occasions when additionally the Poisson fitted value exceeded unity. The relevance of a boundary solution is that it brings about the failure of standard fitting algorithms. The paradox is that this is the circumstance that prompts practitioners to switch to the modified Poisson approach. There are substantial error rates even when the solution is not on the boundary, but the modified Poisson approach is not required in those circumstances because standard software for fitting the LBM should be successful in iterating to the ML solution.