Construction of Minimal Connected Network with Proteins Affected By Expression of the Rol B Plant Oncogene
Tsitsiashvili GSh1*, Bulgakov VP2 and Losev AS1*
1Institute for Applied Mathematics FEB RAS, Vladivostok, Russia
2Institute of Biology and Soil Science FEB RAS, Vladivostok, Russia
Submission: November 17, 2017; Published: January 26, 2018
*Corresponding author: Tsitsiashvili Gurami, Institute for Applied Mathematics FEB RAS, Vladivostok, Russia, Tel: 8-914-693-2749; Email: guram@iam.dvo.ru
How to cite this article: Tsitsiashvili GSh, Bulgakov VP and Losev AS. Construction of Minimal Connected Network with Proteins Affected By Expression of the Rol B Plant Oncogene. Biostat Biometrics Open Acc J. 2018; 4(4): 555644. DOI: 10.19080/BBOAJ.2018.04.555644
Abstract
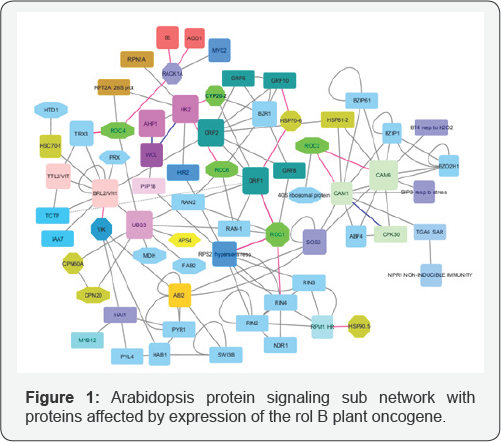
In this paper, a construction of minimal connected network with proteins, affected by expression of the rol B plant oncogene, is making, using concept of connectivity components. In this paper, Arabidopsis protein signaling network G affected by expression of the rol B plant oncogene, is considered. Biochemists experimentally defined in the network G the set U0 of proteins, which tested the effect of the rolB plant oncogene [1].
Clinical Image
All these proteins are marked with octagons on Figure 1. A problem is to define in the network G connected sub network G* with minimal number of proteins including the set of proteins U0 and their nearest neighbors. To solve this problem we calculated minimal ways lengths from proteins, which are not describing by octagons to proteins described by octagons, using Dijkstra algorithm [2]. It is showing that there is the set U1 of 21 proteins with minimal distance 1 to the set U0 , and they are nearest neighbors of proteins describing by octagons on Figure 1. So all, these proteins are to be included to the sub network G* also. In the network G, there are the set U2 of 26 proteins, which have minimal distance 2 to the set U0 and the set U3 of three proteins, which have minimal distance 3 to the set U0 . So total number of proteins in the graph G equals 50. To construct the connected sub network G* , including the sets U0,U1 with minimal number of proteins, we consider the graph Gj with proteins from the sets U0,U1 and edges between them. The graph G1 has two connectivity components G11, G12. . To connect them it is enough to include in the network G* additionally to the sets U0,U1 only the single protein SOS2.
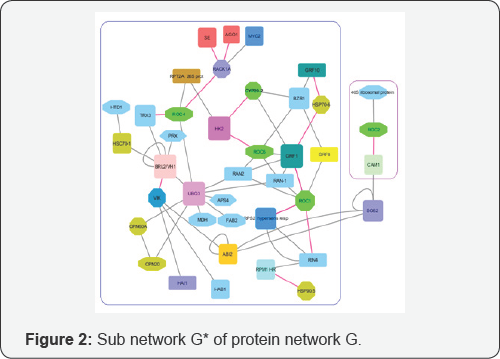
In Figure 2 describe the network G* the sub networks G11, G12 are surrounded by blue and lilac rectangles corresponding. Total number of the graph G* proteins equals 22, not 50 as in the network G. Therefore, main part of proteins of the sets U2,U3 , play in the network G a role of provinces not a role of a connective tissue. This solution is not general for considered mathematical problem, which is N-P problem. Nevertheless, a specific of considered network G allows to construct the sub network G* and to make meaningful interpretation of obtained result using only Cytoscape representation of the network G.






























