Measurement Error in Exposure Doses and Cancer Risk Estimation
Masiuk S1, Kukush A2* and Shklyar S2
1Ukrainian Radiation Protection Institute, Ukraine
2Taras Shevchenko National University of Kyiv, Ukraine
Submission: December 29, 2017; Published: January 24, 2018
*Corresponding author: Alexander Kukush, Professor, The Faculty of Mechanics and Mathematics, Taras Shevchenko National University of Kyiv, Volodymyrska Str. 64, Kyiv 01601, Ukraine, Tel: +380-44-259-0591; Email: alexander.kukush@gmail.com
How to cite this article: Masiuk S, Kukush A, Shklyar S. Measurement Error in Exposure Doses and Cancer Risk Estimation. Biostat Biometrics Open Acc J. 2018; 4(4): 555643. DOI: 10.19080/BBOAJ.2018.04.555643
Abstract
The data used in estimation of radiation exposure dose are not known exactly. We discuss different types of errors which are present in radio-epidemiological models we work with. We illustrate these types or errors in simplified models and share our experience on how the errors of different types affect the estimates of radiation risk parameters.
Keywords: Berkson error; The classical error; Measurement error; Radiation risk estimation; Attenuation effect
Abbreviations: ERR: Excess Relative Risk; EAR: Excess Absolute Risk; GSD: Geometric Standard Deviation .
Opinion
Until recently the most common methods for estimation of radiation risks that associated with human exposure use the assumption of no uncertainty in exposure dose, i.e., it is assumed that we have a determined value for the individual dose of a subject. But now it is clear that such a statement is fundamentally wrong, since in practice there are no situations in which the dose estimated by any method would not have some uncertainty. The nature of the dose uncertainty can be very diverse. E.g., the measurement error can be systematic or random. Systematic under- or overestimation of true values of the exposure dose is known as bias. As a rule a systematic error is not considered as a component of the total error due to the following reason: if a source of such an error is known, then it would be eliminated. In turn a random error can be either shared or unshared. Assume that in a mathematical model used to dose reconstruction for a group of subjects (cohort), some parameters can be the same for subjects of some subgroup. Suppose also that these parameters have uncertainty due to a lack of knowledge of the true value. Then for the subjects of this subgroup, this lack of knowledge is a source of the shared error. In contrast, some parameters can vary stochastically among the subjects of the subgroup, and this is a source of unshared error. So, if parameters are shared, then errors in the parameters are shared as well, leading to a systematic error in dose estimates for the subjects of the subgroup [1].
In addition, the random error can be either classical or Berkson [2]. Let Dtr stand for the true value of exposure dose (usually D‘r is unknown), and Dmes for its measured value. We consider both classical and Berkson errors regarding the logarithms of exposure doses, because measurement errors in doses are multiplicative in their nature. If we have a multiplicative lognormal Berkson dose error, then it holds: xi = Wi + Ui, Ui ∼ N(0,σ2i)Here wi :,= ln(Dmesi) is an observed value, xi := ln(Ditr) is unknown quantity, and ui is normal error with zero expectation and known variance,σi2 . Random variables wi and ui are assumed independent. In case of Berkson error, conditional distribution of xi given wi has a form as follows: xi|wi~ N (wi,σi2 ), i.e., for each observation the conditional distribution of the true value (i.e., of the logarithm of the true dose) is known, but its exact realization is unknown. The Berkson error occurs every time when the dose mean value is applied instead of the dose true value. In particular, if the individual dose values are unknown, but approximated values of their expectations are known, then the replacement of true doses by their approximate expectations leads to measurement errors of Berkson type.
Now, let the dose be observed with the classical log-normally distributed multiplicative error. Then wi = xi + ui, ui ~ N(0,σi2), where xi = ln(Ditr) is unknown value of the logarithm of true dose, wi = ln(Dimes) is known logarithm of the measured dose, xi and ui are independent normal random variables, with zero expectation and known variances (in other words, ui is a random error). In case of the classical error, wi| xi ~ N(xi,σi2) , i.e., conditional distribution of wi has known variance and unknown expectation, the latter is regarded as the logarithm of true dose. The classical error occurs when the measured dose value (i.e., some computational and instrumental dose realization including the error) is used instead of the true dose value. E.g., instrumental measurements of radioactivity fluctuate just because of the presence of the classical error.
One of the consequences from the assumption of the absence of errors in exposure doses is the bias of risk estimates and distortion of the shape of the curve "dose - effect". Notice that such distortions of the risk estimates can be caused not only by systematic errors in dose estimates which is obvious, but by random errors as well. Even though there have been many attempts to include dose errors in the risk analysis lately, the problem is not fully resolved until now. In many cases estimation of dose uncertainty can be expressed as a combination of the classical and Berkson types of error. However, at the moment there is no final conclusion on the impact of the classical, Berkson, or mixed error in dose estimates to the final result of risk analysis, usually being expressed in values of either excess relative risk (ERR) or excess absolute risk (EAR).
As a rule radio-epidemiological studies use the following linear relative risk model:
λ(D,s1,...sp, Z1..., zq ) = exp 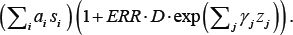 . Here is
the excess relative risk per Gray, a, and γj are regression coefficients, D is the individual exposure dose (in Gray), si are covariates (confounders) that affect the level of background incidence rate (e.g., age, sex, level of examination) and zj are modifying covariates making an effect on the risk of radioinduction (e.g., the age at the moment of exposure, sex).
. Here is
the excess relative risk per Gray, a, and γj are regression coefficients, D is the individual exposure dose (in Gray), si are covariates (confounders) that affect the level of background incidence rate (e.g., age, sex, level of examination) and zj are modifying covariates making an effect on the risk of radioinduction (e.g., the age at the moment of exposure, sex).
Consider the two-parameter linear in dose regression model with binary response: 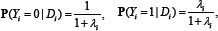 where λi is the total risk or total incidence rate, λi =λ0 +EAR.Di , or as a version with relative risk: λi=λ0(1+EAR.Di )Here Diis the individual exposure dose, λ0 is the background incidence rate (i.e., the one in the absence of the dose factor), ERR is the excess relative risk, EAR=λ0.ERR. is the excess absolute risk. In this instance, λ0 and EAR are positive model parameters to be estimated. The observed sample consists of couples (Y1,Di),i=1,...,N, where Di are the doses (nonnegative numbers); 1iY= in case of morbidity within some time interval, and Yi=0 in the absence of morbidity within the interval.
where λi is the total risk or total incidence rate, λi =λ0 +EAR.Di , or as a version with relative risk: λi=λ0(1+EAR.Di )Here Diis the individual exposure dose, λ0 is the background incidence rate (i.e., the one in the absence of the dose factor), ERR is the excess relative risk, EAR=λ0.ERR. is the excess absolute risk. In this instance, λ0 and EAR are positive model parameters to be estimated. The observed sample consists of couples (Y1,Di),i=1,...,N, where Di are the doses (nonnegative numbers); 1iY= in case of morbidity within some time interval, and Yi=0 in the absence of morbidity within the interval.
To check the influence of classical and Berkson errors in exposure doses on the cancer risk estimation, a simulated stochastic experiment was made. The simulation was performed based on epidemiological studies of thyroid cancer morbidity in Ukraine [3,4]. The absorbed doses of internal thyroid exposure correspond to the published in [5] doses for a real subpopulation of children and adolescents aged from 0 to 18 years (N=13204 persons in total) resided in settlements of Zhytomyr, Kyiv, and Chernihiv oblasts of Ukraine, where direct measurements of thyroid radioactivity were conducted in May–June 1986 [6]. In simulation of the thyroid cancer incidence rate at fixed time interval, the two-parameter logistic linear model of absolute risk was used. The true model parameters were chosen being close to the estimates obtained during epidemiological studies of thyroid cancer in Ukraine [3], namely 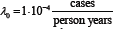 and
and
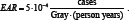 Berkson and the classical errors in exposure doses were simulated separately. It was assumed that both Berkson and classical multiplicative errors in dose are distributed by log-normal law. The error value was set so that its geometric standard deviation GSD = exp(σi) varied from 1.5 to 5, for all i = 1,...,N in the case of the classical error, as well as in the case of Berkson error. In both simulation scenarios, 1,000 data sets were generated for each error value. To estimate the regression parameters λ0 and EAR the naive estimation method (i.e., the one that ignores the presence of errors in doses) was used, Figure 1 & 2.
Berkson and the classical errors in exposure doses were simulated separately. It was assumed that both Berkson and classical multiplicative errors in dose are distributed by log-normal law. The error value was set so that its geometric standard deviation GSD = exp(σi) varied from 1.5 to 5, for all i = 1,...,N in the case of the classical error, as well as in the case of Berkson error. In both simulation scenarios, 1,000 data sets were generated for each error value. To estimate the regression parameters λ0 and EAR the naive estimation method (i.e., the one that ignores the presence of errors in doses) was used, Figure 1 & 2.
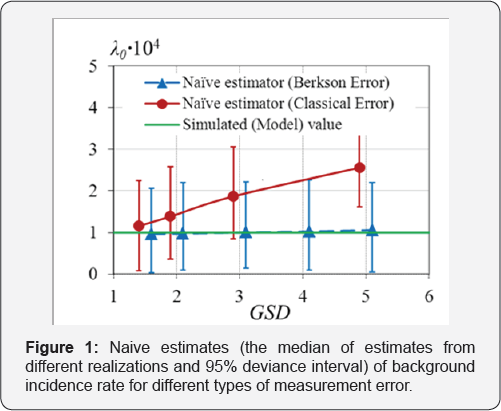
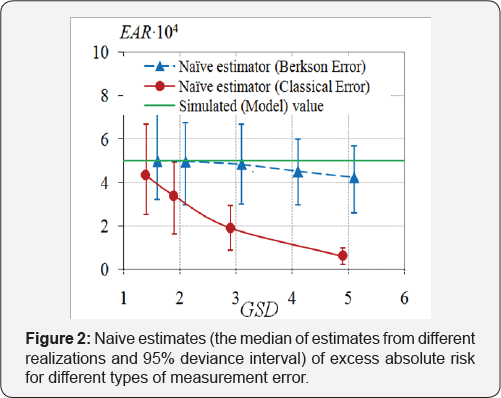
Figure 1 & 2 demonstrate the attenuation effect, i.e., underestimation of excess absolute risk and overestimation of background incidence rate. The effect is more contrast as the error variance is the bias of radiation risk estimates will be significant as well. And the bias of ERR estimates will be larger than the one of EAR estimates.
Our experience tells the following:
o Neglecting of the presence of measurement errors in doses leads to underestimation of both ERR and EAR, if the classical errors are not vanishing.
o Under the absence of the classical errors, Berkson errors do not affect the estimates of regression parameters. Only for huge values of GSD of Berkson errors, the estimates of EAR and ERR are imprecise.
o The larger the variance of the classical error, the worse the estimates of EAR and ERR.
We infer that a close analysis of measurements process is important. Not only the level of measurement errors is important, but also it is crucial which part of the errors constitute the classical ones. The classical errors should be taken into account in construction of the estimates of regression parameters. Berkson errors typically can be neglected if they are not very large. For instance, in radio-epidemiological studies of ecological type, Berkson errors in exposure doses can be quite large, and in this case ignoring Berkson errors will cause significant bias of the EAR and especially ERR estimates.
Notice that standard statistical and epidemiological packages like EPICURE, SAS, SPSS, etc. cannot estimate the affect of measurement errors on the final result. Therefore, in the presence of such errors, one should use specific estimation methods [2] for evaluation of correct estimates of radiation risks. A choice of estimation method depends on the type of error (shared or unshared, multiplicative or additive, the classical or Berkson or their mixture) and on the shape of its distribution. Our experience suggests that a particular method works well for one type of error, but for error of another type, the method can perform even worse than the naive estimation. Thus, in concrete situations, especially under a mixture of errors of different types, it is necessary to make preliminary simulation studies in order to compare the efficiency of estimation methods.
References
- Simon SL, Hoffman FO, Hofer E (2015) The Two-Dimensional Monte Carlo: A New Methodologic Paradigm for Dose Reconstruction for Epidemiological Studies. Radiation Res 183(1): 27-41.
- Masiuk S, Kukush A, Shklyar S, Chepurny M, Likhtarov I (2017) Radiation risk estimation based on measurement error models. De Gruyter, Berlin.
- Tronko MD, Howe GR, Bogdanova TI, Bouville AC, Epstein OV, et al. (2006) A cohort study of thyroid cancer and other thyroid diseases after the Chornobyl accident: Thyroid cancer in Ukraine detected during first screening. J Natl Cancer Inst 98(13): 897-903.
- Bogdanova TI, Zurnadzhy LY, Nikiforov YE, Leeman-Neill RJ, Tronko MD, et al. (2015) Histopathological features of papillary thyroid carcinomas detected during four screening examinations of a Ukrainian-American cohort. Br J Cancer 113(11): 1556-1564.
- Likhtarov I, Kovgan L, Masiuk S, Talerko M, Chepurny M, et al. (2014) Thyroid cancer study among Ukrainian children exposed to radiation after the Chornobyl accident: Improved estimates of the thyroid doses to the cohort members. Health Phys 106(3): 370-396.
- Likhtarov IA, Kovgan LM, Chepurny MI, Masiuk SV (2015) Interpretation of results of radioiodine measurements in thyroid for residents of Ukraine (1986). Probl Radiac Med Radiobiol 20: 185-203.






























