Permutation Statistical Methods: Calculation Efficiencies
Kenneth J Berry1*, Janis E Johnston1, Paul W Mielke Jr2, Howard W Mielke3 and Lindsay A Johnstond4
1Department of Sociology, Colorado State University, USA
2Department of Statistics, Colorado State University, Fort Collins, USA
3Department of Pharmacology, Tulane University, USA
4US Air Force, JBER-Elmendorf Family Health Clinic, USA
Submission: October 17, 2017; Published: January 22, 2018
*Corresponding author: Kenneth J Berry, Department of Sociology, Colorado State University, Fort Collins, USA, Email: berry@mail.colostate.edu
How to cite this article: Kenneth J B, Janis E J, Paul W M Jr, Howard W M, Lindsay A . Permutation Statistical Methods: Calculation Effciencies . Biostat Biometrics Open Acc J. 2018; 4(4): 555640. DOI: 10.19080/BBOAJ.2018.04.555640
Abstract
Permutation statistical methods have much to recommend them as they are distribution-free, appropriate for non-random samples, and provide exact probability values. However, permutation statistical methods, by their very design, are computationally intensive. Eight calculation efficiencies for permutation statistical methods are presented and illustrated with example data sets.
Keywords: Exact methods; Permutation methods; Probability; Mathematical recursion; Resampling methods
Introduction
Permutation statistical methods were initially developed by RA Fisher [1], RC Geary [2], T Eden & F Yates [3], EJG Pitman [4-6] and other mathematicians and scientists in the 1920s and 1930s for validating the normality and homogeneity assumptions of classical statistical methods. Subsequently, permutation statistical methods have emerged as an approach to data analysis in their own right. Permutation statistical methods possess several advantages over classical statistical methods. First, permutation tests are entirely data-dependent in that all the information required for analysis is contained within the observed data. Second, permutation tests are appropriate for non-random samples, such as are common in many fields of research. Third, permutation tests are distribution-free in that they do not depend on the assumptions associated with traditional parametric tests. Fourth, permutation tests provide exact probability values based on the discrete permutation distribution of equally-likely test statistic values. Fifth, permutation tests are ideal for small data sets.
Two types of permutation tests are common in the statistical literature: exact and Monte Carlo resampling tests. Although the two types of permutation statistical tests are methodologically quite different, both types are based on the same specified null hypothesis. In an exact permutation statistical test, the first step is to calculate a test statistic value for the observed data. Second, all possible, equally-likely arrangements of the observed data are enumerated. Third, the desired test statistic is calculated for each arrangement of the observed data. The probability of obtaining the observed value of the test statistic, or one more extreme, is the proportion of the enumerated test statistics with values equal to or more extreme than the value of the observed test statistic. For large samples the total number of possible arrangements can be considerable and exact permutation methods are quickly rendered impractical. For example, permuting two small samples of sizes.
n1 = n2 = 30 yields
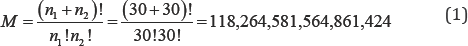
The arrangements of the observed data set-far too many statistical values to compute in a reasonable amount of time.
When exact permutation procedures become intractable, a random subset of all possible arrangements of the observed data can be analyzed, providing approximate, but highly accurate, probability values. Resampling permutation tests generate and examine a Monte Carlo random subset of all possible, equally- likely arrangements of the observed response measurements. For each randomly selected arrangement of the observed data, the desired test statistic is calculated. The probability of obtaining the observed value of the test statistic, or one more extreme, is the proportion of the randomly selected test statistics with values equal to or more extreme than the value of the observed test statistic. With a sufficient number of random samples, a probability value can be computed to any reasonable accuracy. The current recommended practice is to use randomly selected arrangements of the observed data to ensure a probability value L = 1, 000,000 with three decimal places of accuracy [7].
While permutation statistical tests do not require random sampling, normality, homogeneity of variance, or large sample sizes, and are also completely data-dependent, a potential drawback is the amount of computation required, with exact permutation tests formerly being unrealistic for many statistical analyses. Even Monte Carlo resampling permutation tests often require the enumeration of millions of random arrangements of the observed data in order to guarantee sufficient accuracy. For many years, exact tests were considered to be impractical, but modern computers make it possible to generate hundreds of millions of permutations in just a few minutes. In addition, Monte Carlo permutation methods can be inefficient due to millions of calls to a pseudorandom number generator (PRNG).
Eight innovations mitigate this problem. Seven of the eight innovations pertain to both exact and Monte Carlo resampling permutation methods, while the eighth innovation is specific to Monte Carlo resampling methods. First, high-speed computing makes possible exact permutation statistical tests in which all possible arrangements of the observed data are generated and examined. Second, examination of all combinations of arrangements of the observed data, instead of all permutations, yields the identical exact probability values with considerable savings in computation time. Third, mathematical recursion with an arbitrary initial value greatly simplifies difficult computations, such as large factorial expressions. Fourth, calculation of only the variable components of the selected test statistic greatly simplifies calculation. Fifth, for certain classes of problems with a limited number of discrete values it is possible to substantially reduce the number of permutation necessary to accomplish an exact test. Sixth, for matched-pairs and other block designs the required number of arrangements of the observed data can be greatly reduced by holding one set of blocks constant. Seventh, the utilization of partition theory for goodness-of-fit tests can reduce the required number of permutations of the observed data. Eighth, Monte Carlo resampling methods can provide highly-accurate approximate probability values for samples of any size with substantial reduction in calculation. Combinations of any or all of the eight calculation efficiencies provide highly accurate permutation analyses that would otherwise be prohibitive.
High-speed computing
As Berry, Johnston, and Mielke observed in 2014, one has only to observe the hordes of the digitally distracted trying to navigate a crowded sidewalk with their various smart-phones, pads, pods, and tablets to realize that computing power, speed, and accessibility have finally arrived [8]. As Martin Hilbert documented in 2012, just one percent of the world's capacity to store information was in digital format, but by year 2000 digital represented 25 percent of the total world's memory [9]. The year 2002 marked the start of the digital age, as 2002 was the year that humankind first stored more information in digital than in analog form. By 2007 over 97 percent of the world’s storage capacity was digital. Moreover, it was estimated in 2012 that ninety percent of the data stored in the world had been created in just the previous two years. Prior to 2001, data storage was measured in bytes, kilobytes (103) , and occasionally in megabytes (106); now data storage is measured in gigabytes (109) , terabytes (1012), petabytes (1015) , exabytes (1018) , zettabytes (1021) , and even yottabytes (1024) .
In 2000, the Intel Pentium processor contained 42million transistors and ran at 1.5GHz. In the spring of 2010, Intel released the Itanium processor, code-named Tukwila after a town in the state of Washington, containing 1.4billion transistors and running at 2.53GHz. On 4 June 2013 Intel announced the Haswell processor, named after a small town of 65 people in southeastern Colorado with 1.4 billion 3-D chips and running at 3.50GHz. The latest generation of Haswell processors, the i7-4790 processor, currently executes at 4.00GHz with turboboost to 4.40GHz. In April of 2017, Intel introduced the Optane memory module which, when coupled with a seventh generation Intel Core-based system, has the potential to increase desktop computer performance by 28 percent.
Permutation methods
While not widely available to researchers, by 2010 mainframe computers were measuring computing speeds in teraflops. To emphasize the progress of computing, in 1951 the Remington Rand Corporation introduced the UNIVAC computer running at 1,905 flops, which with ten mercury delay line memory tanks could store 20,000 bytes of information; in 2008 the IBM Corporation supercomputer, code-named Roadrunner, reached a sustained performance of one petaflops -a quadrillion operations per second; in 2010 the Cray Jaguar was named the world's fastest computer performing at a sustained speed of 1.75 petaflops with 360 terabytes of memory; and in November of 2010 China exceeded the computing speed of the Cray Jaguar by 57 percent with the introduction of China’s Tianhe-1A supercomputer performing at 2.67 petaflops.
In October of 2011, China broke the petaflops barrier again with the introduction of the Sunway Blue light MPP. In late 2011, the IBM Yellowstone supercomputer was installed at the National Center for Atmospheric Research (NCAR) Wyoming Supercomputer Center in Cheyenne, Wyoming. After months of testing, the Wyoming Supercomputer Center officially opened on Monday, 15 October 2012. Yellowstone was a 1.6 petaflops machine with 149.2 terabytes of memory and 74,592 processor cores and replaced an IBM Bluefire supercomputer installed in 2008 that had a peak speed of 76 teraflops. Also in late 2011, IBM unveiled the Blue Gene\P and \Q supercomputing processing systems that can achieve 20 petaflops. At the same time, IBM filed a patent for a massive supercomputing system capable of 107 petaflops.
From a more general perspective, in 1977 the Tandy Corporation released the TRS-80, the first fully assembled personal computer, distributed through Radio Shack stores. The TRS-80 had 4MB of RAM and ran at 1.78MHz. By way of comparison, in 2010 the Apple iPhone had 131,072 times the memory of the TRS-80 and was about 2,000 times faster, running at one GHz. In 2012, Sequoia, an IBM Blue Gene/Q supercomputer was installed at Lawrence Livermore National Laboratory (LLNL) in Livermore, California. In June of 2012 Sequoia officially became the most powerful supercomputer in the world. Sequoia is capable of 16.32 petaflops-more than 16 quadrillion calculations a second-which is 55 percent faster than Japan's K supercomputer, ranked number 2, and more than five times faster than China’s Tianhe-1A, which was the fastest supercomputer in the world in 2010.
Finally, high-speed computers have dramatically changed the field of computational statistics. The future of high-speed computing appears very promising for exact and Monte Carlo resampling permutation statistical methods. Combined with other calculation efficiencies, it can safely be said that permutation methods have the potential to provide exact or resampling probability values in an efficient manner for a wide variety of statistical applications.
Analysis with combinations
Although permutation statistical methods are known by the attribution "permutation," they are, in fact, not based on all possible permutations of the observed data. Instead exact permutation methods are typically based on all possible combinations of the observed data. Conversely, a combination lock is not based on combinations of numbers or letters, but is instead based on all possible permutations of the numbers or letters. A simple example will illustrate. Consider N = 8 objects that are to be divided into two groups A and B, where nA = nB = 4 The purpose is to compare differences between the two groups, such as a mean or median difference. Let the eight objects be designated { a,b,c,d,e,f,g,h }. For group A, the first object can be chosen in eight different ways, the second object in seven ways, the third in six ways, and the fourth object in five ways. Once these four members of Group A are chosen, the membership of Group B is fixed, since the remaining four objects are assigned to Group B.
Of the 8x7x6x5 =1,680 ways in which the four objects can be arranged for Group A, each individual quartet of objects will appear in a series of permutations. Thus, the quartet { a,b,c,d } can be permuted as { a,b,d,c }, { b,a,c,d }, { c,d,b,a }, and so on. The number of different permutations for a group of four different objects is 4!=4x3x2 x1=24 . Thus, each distinctive quartet will appear in 24 ways among the 1,680 possible arrangements. Therefore, 1,680 divided by 24 yields 70 distinctive quartets that could be formed by dividing eight objects into two groups of four objects each. The number of quartets can conveniently be expressed as

Now, half of these arrangements are similar but opposite. Thus the quartet { a,b,c,d } might be in Group A and the quartet { e,f,g,h } might be in Group B, or vice versa, yielding the same absolute difference. Consequently, there are really only 70/2 = 35 distinctly different pairs of quartets to be considered. The 35 possible arrangements for objects { a,b,c,d } are listed in Table 1 in Gray-code order. The next (36th) possible arrangement would be { a,b,c,h } in Group A and { d,e,f,g } in Group B, which is simply the reverse of arrangement 35, i.e., { d,e,f,g } in Group A and { a,b,c,h } in Group B, yielding the same absolute mean or median difference. A substantial amount of calculation can be eliminated by considering all possible combinations instead of all possible permutations, with no loss of accuracy. In this case, a decrease from 1,680 to 35 arrangements to be considered, a reduction of 98% (Table 1).
Example analysis: Consider a sample of N = 8 objects with values { 38,39,40,43,48,49, 52,57}. The N = 8 objects are divided into two groups, A and B with nA = 4 objects in Group A and nB = 4 objects in Group B. The objects in Group A have values of {43,49,52,57} and the objects in Group B have values of{38,39,40,48}, yielding means 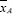 = 50.25 and
= 50.25 and 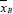 = 41.25, and a mean deference of
= 41.25, and a mean deference of 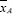 -
- 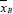 = 50.25 - 41.25 = +9.00. Now consider the data from a permutation perspective. Table 2 lists the 35 possible arrangements of the N = 8 values with nA = nB = 4 preserved for each arrangement, the mean values,
= 50.25 - 41.25 = +9.00. Now consider the data from a permutation perspective. Table 2 lists the 35 possible arrangements of the N = 8 values with nA = nB = 4 preserved for each arrangement, the mean values, 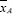 and
and 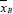 , and the 35 mean differences,
, and the 35 mean differences, 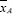 -
- 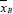 . Inspection of Table 2 reveals that a mean difference of
. Inspection of Table 2 reveals that a mean difference of 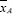 -
- 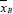 = 50.25 - 41.25 = +9.00 or greater in favor of Group A occurs only twice in the 35 possible arrangements, i.e., row 1 with mean difference +11.50 and row 2 with mean difference +9.00. If Table 2 were to be completed to form all 70 arrangements, a mean difference of 9.00 or greater would also occur twice. Thus, for a two-sided test the exact probability is P = 4/70 = 0.0571, and for a one-sided test the exact probability is P = 2/70 = 0.0286.
= 50.25 - 41.25 = +9.00 or greater in favor of Group A occurs only twice in the 35 possible arrangements, i.e., row 1 with mean difference +11.50 and row 2 with mean difference +9.00. If Table 2 were to be completed to form all 70 arrangements, a mean difference of 9.00 or greater would also occur twice. Thus, for a two-sided test the exact probability is P = 4/70 = 0.0571, and for a one-sided test the exact probability is P = 2/70 = 0.0286.

Mathematical recursion
Mathematical recursion, in a statistical context, is a process in which an initial probability value of a test statistic is calculated, then successive probability values are generated from the initial value by a recursive process. A recursive process is one in which items are defined in terms of items of similar kind. Using a recursive relation, a class of items can be constructed from one or a few initial values (a base) and a small number of relationships (rules). For example, given the base, F0 = 0 and F1 = F2 =1 , the Fibonacci series {0, 1 ,1, 2, 3,5, 8, 13, 21, . . } can be constructed by the recursive rule Fn = Fn-1 +Fn-2 for n > 2 . The initial value need not be an actual probability value, but can be a completely arbitrary positive value by which the resultant relative probability values are adjusted for the initializing value at the conclusion of the recursion process.
A recursion example
Consider a 2 x 2 contingency table using the notation in Table 3. Denote by a plus sign (+) the partial sum of all rows or all columns, depending on the position of the (+) in the subscript list. If the (+) is in the first subscript position, the sum is over all rows and if the (+) is in the second subscript position, the sum is over all columns. Thus, ni+ denotes the marginal frequency total of the ith row, i = 1...r summed over all columns, n+j denotes the marginal frequency total of the jth column, j = 1......c, summed over all rows, and N =n11+n12%n21+n22 denotes the Table 3 frequency total. The probability value corresponding to any set of cell frequencies in a 2x2 contingency table,n11,n12,n21,n22, is the hypergeometric point probability value given by
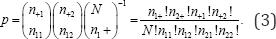
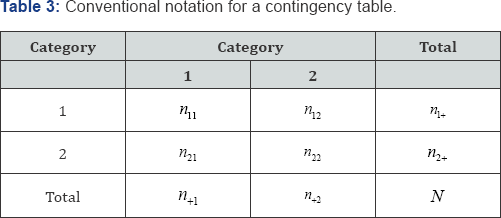
Since the exact probability value of a 2 x 2 contingency table with fixed marginal frequency totals and one degree of freedom is equivalent to the probability value of any one cell, determining the probability value of cell n11 is sufficient. If
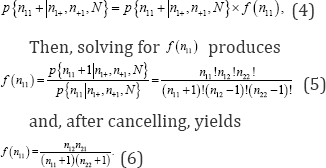
On 18 December 1934, R.A. Fisher presented an invited paper on statistical inference to the Royal Statistical Society, a paper that was subsequently published in the Journal of the Royal Statistical Society [10]. In this paper, Fisher described the logic of permutation statistical methods and provided an example based on 30 criminal same-sex twins from a study originally conducted by Dr. Johannes Lange, Chief Physician at the Munich-Schwabing Hospital in Schwabing, a northern suburb of Munich [11].
The Lange data analyzed by Fisher consisted of 13 pairs of monozygotic (identical) twins and 17 pairs of dizygotic (fraternal) twins. For each of the 30 pairs of twins, one twin was known to be a convict. The study considered whether the twin brother of the known convict was himself "convicted" or "not convicted," thus forming a 2 x 2 contingency table with 12 "convicted" and 18 "not convicted" twins cross-classified by the 13 "monozygotic" and 17 "dizygotic" twins. The 2 x 2 contingency table, as analyzed by Fisher, is presented in Table 4. Fisher determined the reference set of all possible arrangements of the four cell frequencies, given the observed marginal frequency totals. Since there is only one degree of freedom in Table 4, it was only necessary to determine the possible values for one cell. Consider cell nil in the first row and first column of Table 4 with a frequency of 10. For the data in Table 4, there are M = min(n1.,n.1) - max(0,n11,n22) + 1 possible, equally-likely arrangements of cell frequencies in the permutation reference set. Thus, for the frequency data in Table 4.
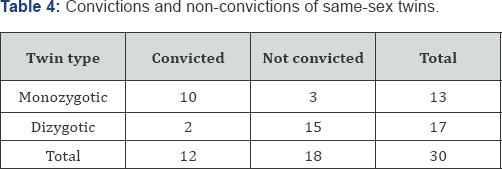
M = min(13, 12)- max(0,10-15) + 1 = 12- 0 +1 = 13 (7)
possible arrangements.
To begin a recursion procedure it is necessary to have an initial value; usually, a beginning probability value. However, it is not necessary to provide an actual probability value to initialize a recursion procedure. Any arbitrary positive value can serve as an initial value with a compensatory adjustment made at the conclusion of the recursion process. The recursion technique can be traced back at least to Lambert Adolphe Jacques Quetelet who used a recursion procedure to generate the binomial probability distribution with p=0.5 and published the technique in a volume with the imposing title Letters Addressed to H.R.H. the Grand Duke of Saxe Coburg and Gotha on the Theory of Probabilities as Applied to the Moral and Political Sciences in 1846 [12]. To illustrate the use of an arbitrary origin in a recursion procedure, consider the data on monozygotic and dizygotic twins in Table 4 and set relative probability value f {n11 = 0|13,12,30} to a small arbitrarily-chosen value, say 1.00; thus, f {n11 = 0|13,12,30} = 1.00. Then following Eq. (6), a recursion procedure produces

The desired exact hypergeometric point probability values are then obtained by dividing each relative probability value,

In this manner, the entire analysis is conducted utilizing an arbitrary initial value and a recursion procedure, thereby eliminating allfactorial expressions.When thenumberofpotential contingency tables given by is large, M = max(n11)-min(n11) + 1 the computational savings can be substantial.
Computing the discrepancies from proportionality equal to or greater than the observed cell frequency configuration in Table 4, the one-tailed hypergeometric probability value for 10, 11, and 12 convicted monozygotic twins is
P = 4.4970 x 10-4 +1.5331 x 10-5 +1.5030 x 10-7 = 4.6518 x 10-4 . (34)
For the frequency data given in Table 4, a two-tailed hypergeometric probability value includes all hypergeometric point probability values equal to or less than the point.
Permutation Methods
Probability value of the observed contingency table, i.e., p{10|13, 12, 30} = 4.4970x10-4. In this case, the additional probabilityvalue associated with Table 4 is p {0|13,12,30} = 7.1534 x 10-5. Thus, the two-tailed hypergeometric probability value is
p{nu = 5113,12,30} = 4’044.8571 = 2.8938x 10-1, (26)
P = 4.4970x10-4 + 1.5331x 10-5 + 1.5030x10-7 + 7.1543 x10-5 = 5.3672x10-4 (35)
Variable components of a test statistic
Under permutation, only the variable components of the test statistic need be calculated for each arrangement of the observed data. As this is often only a very small piece of the desired test statistic, calculations can often be reduced by several factors [13]. For example, in 1933 Thomas Eden and Frank Yates substantially reduced calculations in a randomized- block analysis of Yeoman II wheat shoots by recognizing that the block and total sums of squares would be constant for all of their 1,000 random samples and, consequently, the value of Z for each sample would be uniquely defined by the treatment (between) sum of squares, i.e., the treatment sum of squares was sufficient for a permutation test of a randomized-block analysis of variance [5]. To illustrate an analysis using only the variable components of a test statistic, consider the expression for a conventional two-sample test t,
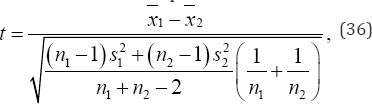
where n1 and n2 denote the sample sizes, S21 and S22 denote the estimated population variances, 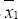 and
and 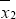 and denote the sample means for samples 1 and 2, respectively. In computing the permutation probability value of Student’s two-sample t test, given the total of all response measurements
and denote the sample means for samples 1 and 2, respectively. In computing the permutation probability value of Student’s two-sample t test, given the total of all response measurements

Where x1i and x2i denote the response measurements in samples 1 and 2, respectively, only the sum of the response measurements in the smaller of the two samples need be calculated, for each arrangement of the observed response measurements, i.e.,  , where denotes a response measurement in sample 1 and n1 ≤ n2. Computing only the variable components of the test statistic thus eliminates a great deal of calculation for each random arrangement of the observed data, a time-saving technique utilized by E.J.G. Pitman in his 1937 permutation analysis of two independent samples. For a second example, consider Pearson’s product-moment correlation coefficient between variables x and y given by
, where denotes a response measurement in sample 1 and n1 ≤ n2. Computing only the variable components of the test statistic thus eliminates a great deal of calculation for each random arrangement of the observed data, a time-saving technique utilized by E.J.G. Pitman in his 1937 permutation analysis of two independent samples. For a second example, consider Pearson’s product-moment correlation coefficient between variables x and y given by
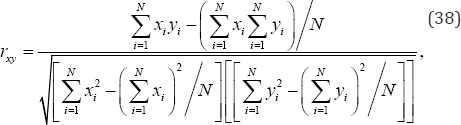
Where, N is the number of bivariate measurements. N and the summations
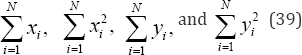
are invariant under permutation. Thus, it is sufficient to calculate only 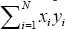 for the observed data and all permutations of the observed data, eliminating a great deal of unnecessary calculation. In addition, it is only necessary to permute either variable x or variable y , leaving the other variable fixed.
for the observed data and all permutations of the observed data, eliminating a great deal of unnecessary calculation. In addition, it is only necessary to permute either variable x or variable y , leaving the other variable fixed.
For a third example, consider Kendall's τb coefficient of ordinal association. A number of measures of association for two ordinal-level variables are based on pairwise comparisons of differences between rank scores. The test statistic S, as defined by Maurice Kendall in 1938 and more extensively in 1948, plays an important role in a variety of statistical measures where Kendall’s test statistic is often expressed as S = C-D , whereC and D indicate the number of concordant pairs and discordant pairs, respectively [14,15]. Consider two ordinal variables that have been cross-classified into a rx c contingency table, where r and c denote the number of rows and columns, respectively. Let ni+, nj+, and nij denote the row marginal frequency totals, column marginal frequency totals, and number of objects in the ijth cell, respectively, for i = 1,...,r and j = 1,. . . ,c, and let N denote the total number of objects in the r x c contingency table, i.e.,
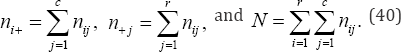
Kendall's τb coefficient of ordinal association between variables X and y given by
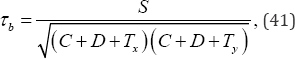
Where, for an r × c contingency table C denotes the number of pairs of objects that are ranked in one order on both variable x and y given by

D denotes the number of pairs of objects that are ranked in one order on variable x and the reverse order on variable y given by
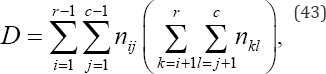
Tx denotes the number of pairs tied on variable x but not tied on variable y given by
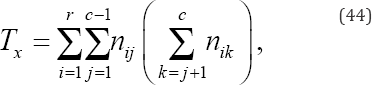
And Ty denotes the number of pairs tied on variable y but not tied on variable x given by
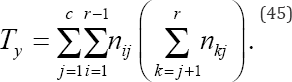
To illustrate the calculation of Kendall’s Tτ test statistic, consider the frequency data given in Table 5, where N = 41 bivariate observations have been cross-classified into a 3 x 3 ordered contingency table. For the frequency data given in Table 5, the number of concordant pairs following Eq. (42) is


S =CD=249 -125=+124, and the observed value of Kendall's τ test statistic is

It is not generally recognized that C+D+Tx, and C+D+TY can be obtained from the observed marginal frequency totals, which are invariant under permutation. Thus,

Since, the marginal frequency distributions are fixed under permutation, the exact probability value of Kendall’s τb is based entirely on the permutation distribution of S . Not only does this hold for Kendall's τb , but it also holds for other test statistics with in the numerator, including Kendall’s τa , Stuart's τc , and Somers’ dyx and dxy measures of ordinal association.
For an exact permutation analysis of an r x c contingency table, it is necessary to calculate the selected measure of ordinal association for the observed cell frequencies and exhaustively enumerate all m possible, equally-likely arrangements of the N objects in the rc cells, given the observed marginal frequency distributions. For each arrangement in the reference set of all permutations of cell frequencies a measure of ordinal association, say S , and the exact hypergeometric point probability value under the null hypothesis, p(nij|ni+,n+j,N) , are calculated,
Where,
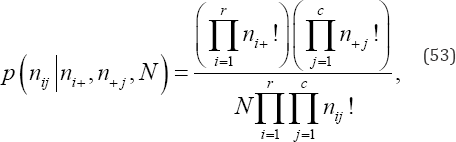
nij is an observed cell frequency for i = 1,...r and j = 1,...,c,ni+ is the ith of row marginal frequency totals summed over all columns, n+, is the jth of column marginal frequency totals summed over all rows, and N is the total of all nu values for i = 1,...r and j = 1,...,c. If So denotes the value of the observed test statistic, the exact one-sided upper- and lower-tail probability (P) values of So are the sums of the p(nij|ni+,n+j,N) values associated with the S values computed on all possible, equally-likely arrangements of cell frequencies that are equal to or greater than So when So is positive and equal to or less than So when So is negative, respectively. Thus, the exact hypergeometric probability value of So when S is positive is given by
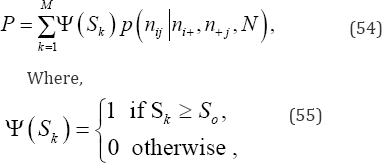
and the exact hypergeometric probability value of So when S is negative is given by
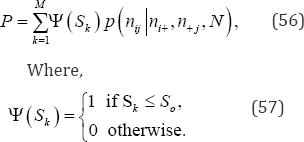
For the frequency data given in Table 5, there are only M = 5,225 possible, equally-likely arrangements in the reference set of all permutations of cell frequencies given the observed row and column marginal frequency distributions, {16,14,11} and {15,10,16}, respectively, making an exact permutation analysis possible. The exact probability value of Kendall's S under the null hypothesis is the sum of those hypergeometric point probability values associated with values of S = +124 or greater. Based on the hypergeometric probability distribution, the exact upper-tail probability value is P = 0.0555.
Limited number of discrete values
Simple linear correlation with one predictor variable requires the enumeration of N! possible arrangements of the observed data when N determining an exact probability value. When is large, the number of possible arrangements can be excessive. For example, with only N = 15 paired values there are
M=15! =1,307,674,368,000 (58)
arrangements to be enumerated and analyzed. In such cases, Monte Carlo resampling permutation methods can be utilized, in which a random sample of size L is drawn from the reference set of all m possible arrangements. The probability value is simply the proportion of sampled correlation coefficients equal to or more extreme than the observed correlation coefficient value. While the resulting probability value is approximate, when L is large the probability value can be highly accurate. In general, a sample of l = 1,000,000 random arrangements is sufficient to ensure three decimal place of accuracy. However, L = 100,000,000 random arrangements is required to ensure four decimal places of accuracy.
Under special circumstances, there is an alternative for determining an exact probability value. Occasionally, correlation data is gathered in which one of the variables has only a limited number of unique values. The limiting case occurs when, for example, y variable is a continuous interval-level variable and variable X is a simple dichotomy, such as in point-biserial correlation. However, there are other cases in which only a few distinct values appear in variable , e.g., three or four values. An exact analysis can then be conducted by treating the distinct values of variable x as groups and correlating the continuous variable with group membership, with considerable increase in calculation efficiency
To illustrate the analysis technique, consider N = 12 paired X and y values where variable X is a simple dichotomy. The number of objects in group 1 are indicated by n, =6 and the number of objects in group 2 are indicated by n2 = 6. There are
M =N! =12!=479,001,600 (59)
possible arrangements ofthe observed data to be enumerated and analyzed. However, treating the data as consisting of two groups with n1 = n2 = 6, there are only

arrangements to be examined. If, for example, the groups are not of equal size and N =12, n1 = 7 and n2 = 65, then there are only
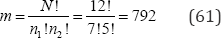
arrangements to be examined. If N = 12 and there are three distinct values of variable X where n1= n2=n3= 4, then there are
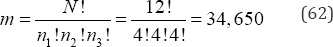
arrangements to be examined. As with a simple dichotomy, as the group sizes diverge, the number of possible arrangements to be examined is further reduced. For example, if N = 12, n1 = 3, n2 = 4, and n3 = 5, then there are only
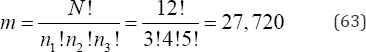
arrangements to be examined.
Two examples illustrate the computational efficiency of analyzing group structures. First, consider the correlation data listed in Table 6. The data in Table 6 consist of N = 12 subjects divided into two groups with seven Republicans (R) in group 1 and five Democrats (D) in group 2. The raw data are listed on the left side of Table 6 and the dummy-coded (0, 1) values are listed on the right side. A dummy code of 1 indicates that the subject is in group 1, i.e, is a Republican, and a dummy code of 0 indicates that the subject is not in group 1, i.e., is a Democrat.

For the paired data listed in Table 1, N = 12 , n1 = 7, n2 = 5, and the product-moment correlation between variables X and y is rxy = +0.3672. Treating variable x as two groups, there are only
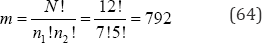
arrangements to be examined. There are 212rxy values equal to or more extreme than the observed value of rxy = + 0.3672. If ro denotes the observed value of the exact two-sided probability value of ro = +0.3672 is
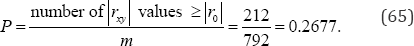
In contrast, for an exact analysis of all M =N! =12!= 479,001,600 (66)
arrangements of the observed data, there are 128,220,580rxy values equal to or more extreme than the observed value of rxy =+0.3672. If denotes the observed value of rxy, the exact two-sided probability value of ro = +0.3672 is
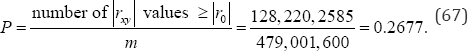
For a second example, consider the correlation data listed in Table 7. The data in Table 7 consist of N = 12 subjects divided into three groups with four Republicans (R) in group 1, four Democrats (D) in group 2, and four independents (I) in group 3. The raw data is listed on the left side of Table 7 and the dummy- coded (0, 1) values are listed on the right side. A dummy code of (1, 0) indicates that the subject is in group 1, i.e., is a Republican, a dummy code of (0, 1) indicates that the subject is not in group 1, but is in group 2, i.e., is a Democrat, and a dummy code of (0, 0) indicates that the subject is not in groups 1 or 2, but is in group 3, i.e., is an Independent.
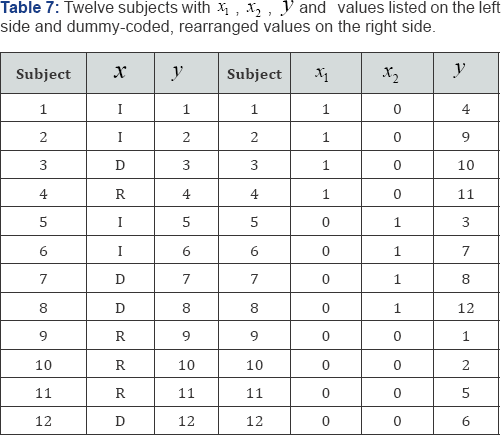
For the paired data listed in Table 7, N = 12, n1 = n1 = n1 = n1, and the product-moment correlation between the linear combination of variables x1 and x2 with variable y is R =+0.3916

arrangements to be examined. There are 3,948Ry.x1,x2 , values equal to or more extreme than the observed value of Ry.x1,x2 =+0.3916. If Ro denotes the observed value of Ry.x1,x2 the exact two-sided probability value of Ry.x1,x2 =+0.3916 is
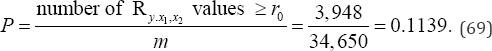
In contrast, for an exact analysis of all M=N! =12!= 479,001,600 (70)
arrangements of the observed data, there are 54,576,484Ry.x1,x2 values equal to or more extreme than the observed value of Ry.x1,x2 = 0.3916. Ro denotes the observed value of Ry.x1,x2 the exact two-sided probability value of Ry.x1,x2 = 0.3916.
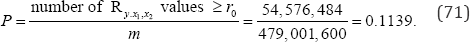
In this manner, when there is a limited number of distinct values in one or more variables, the number of possible arrangements of the observed data can be reduced substantially and an exact analysis conducted where an examination of all N! arrangements would be prohibitive.
Fixed measurements
In matched-pairs and other block designs where the same, or matched, subjects are measured on two or more occasions, the number of possible arrangements of the observed data can become quite large. Holding one set of measurements constant, relative to the other set(s), can greatly reduce the number of arrangements to be analyzed. In 1939 Maurice Kendall and Bernard Babington Smith published an article in The Annals of Mathematical Statistics on "The problem of m rankings" in which they developed the well-known coefficient of concordance [16]. Let N and m denote the number of rank scores and the number of judges, respectively, then Kendall and Babington Smith defined the coefficient of concordance as

Where, S is the observed sum of squares of the deviations of sums of ranks from the mean value m (N + +)/2. In a form more conducive to calculation, W can be defined as

Where, R for i = 1,...,N is the sum of the rank scores for the ith of N objects and there are no tied rank scores. Since m2 (N3 -N) in the denominator of Eq. (72) is invariant over all permutations of the observed data, Kendall and Babington Smith showed that in order to test whether an observed value of W is statistically significant it is only necessary to consider the distribution of S by permuting the N ranks in all possible, equally-likely ways. There are
M = (N !)m (74)
possible arrangements of the observed data to be analyzed. However, letting one of the rankings be fixed, relative to the other m -1 rankings, there are only
M = ( N !)m-1 (75)
arrangements to be considered.
Example
To illustrate Kendall and Babington Smith's coefficient of concordance, consider the rank data listed in Table 8 with N = 8 objects and m = 3 sets of rankings. For the rank scores listed in Table 8, the sum of the squared rank scores is
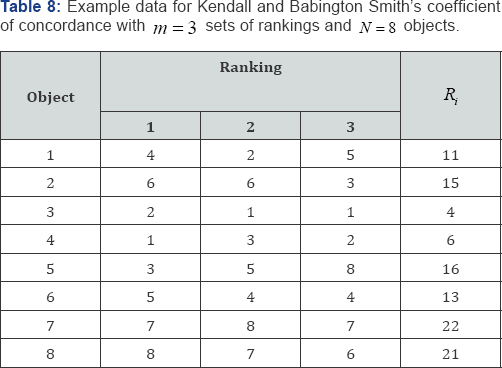
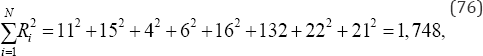
the observed value of Kendall and Babington Smith’s coefficient of concordance is
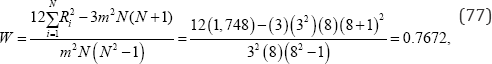
For the m = 3 sets of rank scores listed in Table 7 there are M =( N !)m =(8!)3 = 65,548,320,768,000 (78)
possible arrangements of the observed data- too many for an exact permutation analysis. However, holding one set of rank scores constant relative to the other two sets of rank scores reduces the number of possible arrangements to
M = (N !)m = (8 !)3 = 1,625,702,400 (79)
While even this number of possible arrangements makes an exact permutation analysis impractical, it is not impossible. If the reference set of all M arrangements of the observed rank scores listed in Table 8 occur with equal chance, the exact probability of W = 0.7672 under the null hypothesis is
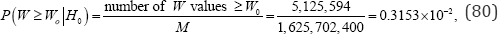
Where,w denotes the observed value of W .
Partition theory
Goodness-of-fit tests are common in contemporary research. Among the more popular goodness-of-fit tests are Pearson’s chi-squared test (x2) [17], Wilks' likelihood-ratio test (G2) [18,19], the Freeman-Tukey test (T2) [20], and the Cressie-Read test (I(λ)) [4]. In this section goodness-of-fit tests for unordered equiprobable categories are described and compared. Included in this section are Fisher’s exact test, exact chi-squared, exact likelihood-ratio, exact Freeman-Tukey, and exact Cressie-Read goodness-of-fit tests for k disjoint, unordered categories with equal probabilities under the null hypothesis. Exact tests are free from any asymptotic assumptions; consequently, they are ideal for sparse tables where expected values may be small. Consider the random assignment of N objects to k unordered, mutually-exclusive, exhaustive, equiprobable categories, i.e., the probability for each of the k categories is p. = 1/ k for i = 1,..., k under the null hypothesis. Then, the probability that Oi objects occur in the ith of k categories is the multinomial probability given by
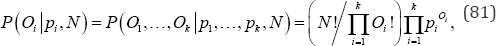
Fisher’s exact goodness-of-fit test is the sum of all distinct P(Oi|N,pi) values that are equal to or less than the observed value of P(Oi|N,pi) associated with a set of observations,O1......Ok [21]. The Pearson chi-squared goodness-of-fit test statistic for N objects in k disjoint, unordered categories is given by
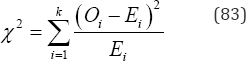
and Wilks’ likelihood-ratio test statistic is given by
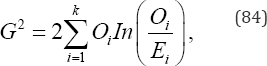
Where, the expected frequency of the ith category under the null hypothesis of equal category probabilities is given by

Two other tests that have received attention are the Freeman- Tukey [9] goodness-of-fit test given by
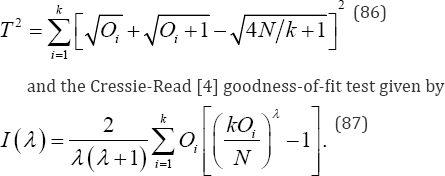
Cressie and Read showed that I (λ) with λ set to 2/3 was optimal both in terms of attained significance level and small sample properties. In general, for an exact goodness-of-fit test with N objects in k categories there are
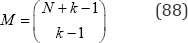
distinct ordered arrangements to be examined. Under the null hypothesis that the probabilities of all k categories are equal, a vastly reduced number of distinct partitions of the data can be considered using a further condensation of the M ordered configurations. The condensation is based on a 1748 result by Leonhard Euler that provides a generating function for the number of decompositions of N integer summands without regard to order using the recurrence relation
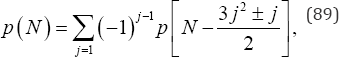
Where p(0) = 1 and is a positive integer satisfying 2≤ 3j2 ± j≤2N . Note that if N = 1, then j = 1, with only the minus (-)sign allowed; if 2 ≤ N ≤ 4, then j = 1, with both the plus (+) and minus (-) signs allowed; if 5 ≤ N ≤ 6, then j = 1 with both the plus (+) and minus (-) signs allowed and j = 2 with only the minus (-) sign allowed; and so forth. G.H. Hardy and S. Ramanujan [22] provided the asymptotic formula for p (N) given by
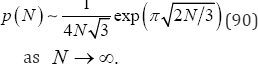
Given disjoint, unordered categories and observed categorical frequencies o,,..., ok, an algorithmic procedure generates all p (N) partitions, computes the exact probability for each partition, calculates the observed X2,G2,T2, and I (λ) test statistic values, and calculates the number of ways that each partition can occur, i.e., the partition weights [23]. The partition weights are multinomial and are given by
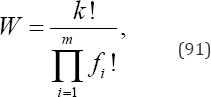
Wherefi is the frequency for each of m distinct integers comprising a partition. For example, if the observed partition {3 2 2 1 0 0} is where n = 8 objects, k = 6 categories, m = 4 and distinct integers (3,2,1,0), then f1 = 1, f2 = 2, f3 = 1, f4 = 2, and
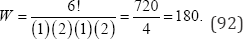
If k < N , the number of distinct partitions is reduced to eliminate those partitions where the number of partition values exceeds k . For example, if k = 3 and N = 5, then the two partitions {2 1 1 1} and {1 1 1 1 1} cannot be considered as the respective number of partitions, four and five, both exceed k = 3 . The sum of the values of W for the included distinct partitions is equal toM . The exact probability values for the Fisher exact, Pearson x2, Wilks G2, Freeman-Tukey T2, and Cressie-Read I (!) goodness-of-fit tests are obtained by comparing observed values to partition probability values. In the case of Fisher’s exact test, partition probability values equal to or less than the observed partition probability value are weighted and summed. For the exact %2, G2, T2, and I (λ) goodness-of-fit tests, partition probability values associated with partition test statistics equal to or greater than the observed test statistic values are weighted and summed.
Example
Consider that a patient is asked to check any of k = 50 symptoms experienced in the past six months, resulting in N = 10 selections for categorical frequencies of O1 = 4, O2 = 3, O3 = 2, O4 = 1, and O5 =... = O50 = 0. The null hypothesis specifies that the k expected category probabilities are equally likely, i.e., pi = 1/k = 1/50 = 0.02 for i = 1, , 50. Fisher's i = 1...50. exact probability value is 0.1795x10-5. Under the null hypothesis of no difference between the observed and expected cell frequencies, the observed Pearson uncorrected chi-squared test statistic is X2 = 140.00 with an exact probability value of P = 0.3788 x10-4, the observed Wilks likelihood-ratio test statistic is G2 = 52.64 with an exact probability value of P = 0.1795 x1°-5, the observed Freeman- Tukey test statistic is T 2 = 23.87 with an exact probability value of P = 0.1795 x10-5, and the observed Cressie-Read test statistic is I (2/3) = 89.87 with an exact probability value of P = 0.8356 x10-5. Table 9 lists the exact probability values for the Fisher exact, Pearson x2, WilksG2, Freeman-Tukey T2, and Cressie-Read I (2/3) test statistics and illustrates the analysis of very sparse data with N =10 observations in k = 50 unordered equiprobable categories[24-26].
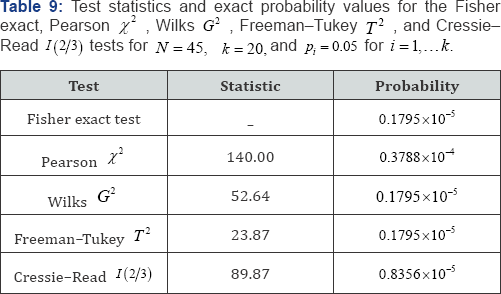
For the example analyses in Table 9 there are only p (1°) = 42 partitions of the observed data to be examined. On the other hand, for a conventional analysis there are
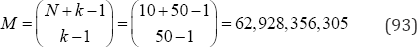
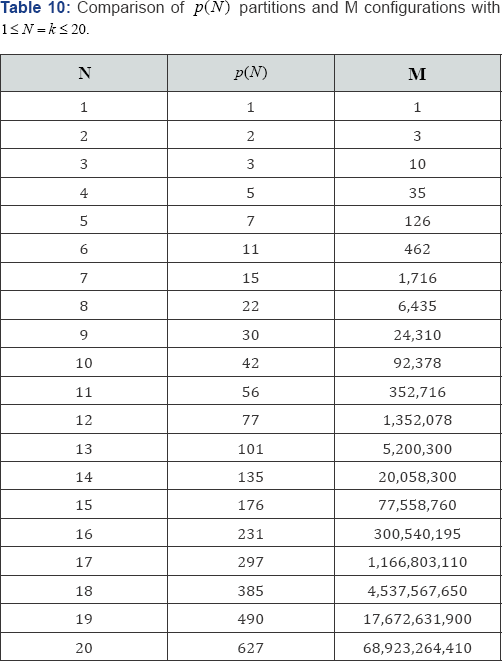
arrangements to be examined. The use of partitions based on p(N) with equal category probabilities is highly efficient when compared with the calculation of test statistic values based on all M possible configurations. Table 10 compares the p(N) partitions with the M possible configurations for 1 ≤ N = k ≤ 20. For example, with N = 15 observations in k = 15 categories, there are only p (15) = 176 partitions, but
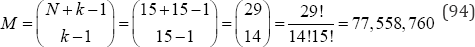
Monte carlo resampling
When exact permutation procedures become unmanageable due to the large number of possible arrangements of the observed data, a random sample of the M possible arrangements can be substituted, providing approximate, but highly accurate, probability values. Resampling permutation tests generate and examine a Monte Carlo random sample of all possible, equally- likely arrangements of the observed response measurements. For each randomly selected arrangement of the observed data, the desired test statistic is calculated. The probability of obtaining the observed value of the test statistic, or one more extreme, is the proportion of the randomly selected test statistics with values equal to or more extreme than the value of the observed test statistic. With a sufficient number of random samples, a probability value can be computed to any reasonable accuracy. While exact permutation methods are restricted to relatively small samples, given the large number of possible arrangements of the observed data, Monte Carlo resampling permutation tests are not limited by the sizes of the samples.
Monte Carlo resampling permutation tests have been shown to provide good approximations to exact probability values as a function of the number of random arrangements considered. The number of random arrangements suggested in books and articles is varied and likely dated due to previous limitations of computer speed and memory. Some authors have proposed as few as 100 random arrangements to as many as 10,000. For many years, 10,000 random arrangements was the most common number cited and the default value in many commercial resampling programs. More recently, 1,000,000 random arrangements appears to be the number most in use [13]. To illustrate the number of random arrangements required to yield a predetermined number of decimal places of accuracy, consider the data listed in Table 11. The data listed in Table 11 are adapted from Berry, Mielke, and Mielke and represent soil lead (Pb) quantities from two school districts in metropolitan New Orleans. There are
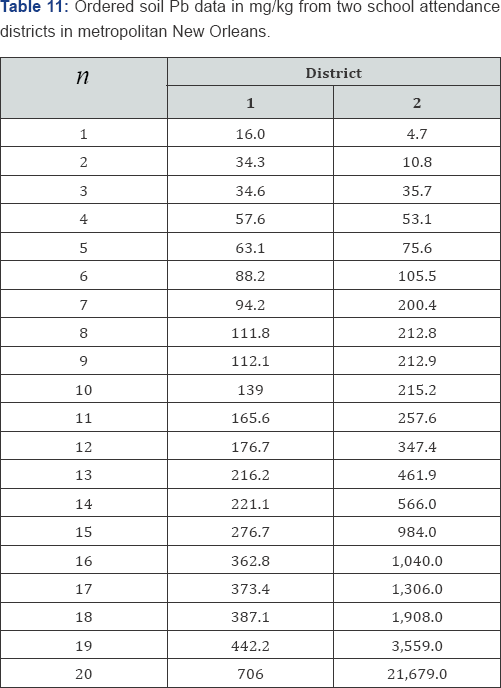
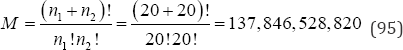
possible arrangements of the soil lead data listed in Table 11 to be considered. Table 12 summarizes the results for eight different resamplings (L) of the data listed in Table 11 and the associated two-sided probability values. Each of the probability values was generated using a common seed and the same pseudorandom number generator. The last row of Table 12 contains the exact probability value based on all M = 137,846,528,820 possible arrangements of the soil lead data listed in Table 11. Given the results of the Monte Carlo resampling probability analyses listed in Table 12, l = 1,000,000 appears adequate when three decimal places of accuracy are required. Little improvement is achieved with increasing numbers of permutations. l = 1,000,000 provides a combination of accuracy and practicality. Modern desktop computers can generate 1,000,000 random arrangements in just a few seconds. For a second example analysis of a Monte Carlo resampling analysis consider the frequency data given in Table 13 where N = 72 bivariate observations have been crossclassified into a 3x 5 ordered contingency table.
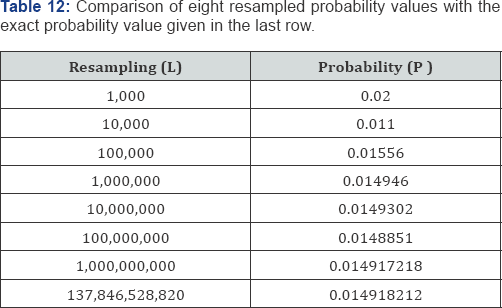
To calculate an exact probability value for a contingency table it is necessary to exhaustively enumerate all possible arrangements of cell frequencies, given the observed marginal distributions, calculate the specified test statistic on each arrangement, compute the hypergeometric point probability value for each arrangement of the observed data, and sum the hypergeometric point probability values associated with those test statistic values that are equal to or more extreme than the test statistic value calculated on the observed contingency table. A hypergeometric probability value, p (nij|ni+, n+j, N), is given by

Where, nij is an observed cell frequency for i = 1,...r and j = 1,... c, ni+ is the ith of row marginal frequency totals summed over all columns,n+ is the j of column marginal frequency totals summed over all rows, and N is the total of all nij values for i = 1,...r and j = 1,...c. On the other hand, Monte Carlo resampling only requires counting the number of test statistic values that are equal to or greater than the observed test statistic value-no hypergeometric probability values are required. The Monte Carlo resampling probability value is simply the proportion of test statistic values computed on the randomly selected arrangements that are equal to or greater than the observed test statistic value. For the frequency data given in Table 13, Kendall's measure of ordinal association as given in Eq. (41) is τb = +0.1664. For the data given in Table 13, there are m = 70,148,145 possible, equally-likely arrangements in the reference set of all permutations of cell frequencies given the observed row and column marginal frequency distributions, {23,23,26} and {15,11,14,17,15}, respectively. Therefore, an exact test may not be practical and a Monte Carlo resampling probability analysis based on L random arrangements of cell frequencies is utilized. The resampling probability value of τb under the null hypothesis isthe number of τb values equal to or greater than τb =+0.1664; in this case the Monte Carlo resampling approximate upper-tail probability value based on L = 1,000,000 is

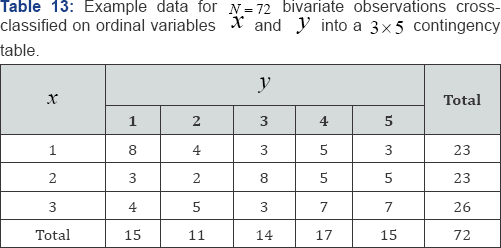
Where, τo denotes the observed value of τb .While an exact permutation analysis is not practical for the frequency data given in Table 1, it is not impossible. The exact probability value of Kendall's τb under the null hypothesis is the sum of those hypergeometric point probability values associated with values of τb = +0.1664 or greater. Based on the hypergeometric probability distribution, the exact upper-tail probability value conditioned on the reference set of all M = 70,148,145 arrangements of cell frequencies is
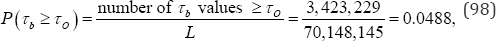
A Monte Carlo resampling analysis not only examines a small fraction of the M possible arrangements of the observed data but, as in this example analysis, eliminates the calculation of 70,148,145 hypergeometric point probability values for a substantial increase in calculation efficiency.
Discussion
Eight improvements to permutation statistical methods are described to improve calculation efficiency. First, high-speed computers can quickly generate a large number of arrangements of the observed data, be these all possible arrangements or a large number of random arrangements. Second, substitution of all possible combinations for permutations yields the same probability values with a great reduction in computing time. Third, mathematical recursion greatly simplifies difficult calculations. Fourth, analysis of only the variable components of a specified test statistic eliminates many non-essential calculations. Fifth, when one variable contains only a small number of different values, substantial savings can be achieved by treating the different values as groups with no loss of precision. Sixth, For certain classes of problems, e.g., block designs, fixing one of the variables relative to the other variables can reduce the number of arrangements that need to be examined. Seventh, the use of partition theory in goodness-of-fit tests greatly reduces the number of required arrangements of the observed data. Eighth, Monte Carlo resampling methods can provide highly- accurate approximate probability values for samples of any size with substantial reduction in calculation. The first seven are methods to improve calculation of exact probability values, but may also be used with Monte Carlo resampling values. While any one of the eight improvements may be used independently of the others, when used in combination with one or more of the others, vastly improved computation times can be achieved.
References
- Fisher RA (1925) Statistical Methods for Research Workers. In: Oliver B, Edinburgh, Biological Monographs and Manuals, Pg no. 1-250.
- Geary RC (1927) Some properties of correlation and regression in a limited universe, Metron 7: 83-119.
- Eden T, Yates F (1993) On the validity of Fisher’s z test when applied to an actual sample of non-normal data. J Agric Sci 23: 6-17.
- Pitman EJG (1937) Significance tests which may be applied to samples from any populations Suppl J Royal Stat Soc 4: 119-130.
- Pitman EJG (1937) Significance tests which may be applied to samples from any populations: II. The correlation coefficient test. Suppl J Royal Stat Soc 4: 225-232.
- Pitman EJG (1938) Significance tests which may be applied to samples from any populations: III. The analysis of variance test, Biometrika 29: 322-335.
- Johnston JE, Berry KJ, Mielke PW (2007) Permutation tests: Precision in estimating probability values. Percept Mot Skills 105 (3): 915-920.
- KJ Berry, JE Johnston, Mielke PW (2014) A Chronicle of Permutation Statistical Methods, Springer-Verlag, Cham, USA.
- Hilbert M (2012) How much information is there in the "information society”? Significance 9(4): 8-12.
- Fisher RA (1935) The logic of inductive inference. J Royal Stat Soc 98(1): 39-82.
- Lange J (1931) Crime as Destiny: A Study of Criminal Twins, Allen & Unwin, London.
- Quetelet LAJ (1849) Letters Addressed to H.R.H. the Grand Duke of Saxe Coberg and Gotha, on the Theory of Probabilities as Applied to the Moral and Political Sciences, Charles & Edwin Layton, London, 1849.
- Scheffe H (1959) The Analysis of Variance, Wiley, New York, Pp. 477.
- Kendall MG (1938) A new measure of rank correlation Biometrika 30(1-2): 81-93.
- Kendall MG (1948) Rank Correlation Methods, Griffin, London.
- Kendall MG, Babington S (1939) The problem of m rankings. Ann Math Stat 10(3): 275-287.
- Pearson K (1900) On the criterion that a given system of deviations from the probable in the case of acorrelated system of variables is such that it can be reasonably supposed to have arisen from random sampling, Philos Mag 50: 157-175.
- Wilks SS (1935) The likelihood test of independence in contingency tables. Ann Math Stat 6(4): 190-196.
- Wilks SS (1938) The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann Math Stat 9(1): 60-62.
- Freeman MF, Tukey JW (1950) Transformations related to the angular and the square root, Ann Math Stat 21(4): 607-611.
- Cressie N, Read TRC (1984) Multinomial goodness-of-fit tests. J Royal Stat Soc B 46:440-464.
- Hardy GH, Ramanujan S(1918) Asymptotic formulae in combinatory analysis, Proc Lond Math Soc 17 (1): 75-115.
- Mielke PW, Berry KJ (1993) Exact goodness-of-fit probability tests for analyzing categorical data. Educ Psychol Meas 53: 707-710.
- Berry KJ, Johnston JE, Mielke PW (2004) Exact goodness-of-fit tests for unordered equiprobable Categories. Percept Mot Skills 98(3): 909918.
- Berry KJ, Mielke PW, Mielke HW (2002) The Fisher-Pitman permutation test: An attractive alternative to the F test. Psych Rep 90(2): 495-502.
- Euler L (1988) Introduction to Analysis of the Infinite, Springer-Verlag, New York.






























