Biostatistics and Biometrics Open Access Journal

Opinion

A Comparison of Two Matrices for Testing Covariance Matrix in Unbalanced Linear Mixed Models

Barnabani M*

Department of Statistics Informatics Applications, University of Florence, Italy

Submission: September 12, 2017; Published: October 12, 2017

*Corresponding author: Barnabani Marco, Department of Statistics Informatics Applications, University of Florence, Italy, Tel: +39 055 2751500; Email: barnaban@disia.unifi.it

How to cite this article: Marco B. A Comparison of Two Matrices for Testing Covariance Matrix in Unbalanced Linear Mixed Models. Biostat Biometrics Open Acc J. 2017; 3(3): 555611. DOI: 10.19080/BBOAJ.2017.03.555612

Abstract

Despite the widespread use of mixed-effects regression model, available methods for testing the covariance matrix of random effects are quite limited. In these cases, because of complexity and difficulties coming from an analysis of multiple variance components, inference based on testing the equality of two positive semi definite matrices seems most appropriate. We propose a test statistic based on a comparison between an estimate of a covariance matrix defined when data come from a linear regression model (covariance matrix zero) and an appropriate sample variance covariance matrix. We show that under the null hypothesis the test statistic is close to one and under the alternative it is expected to be larger than one. The objectives of the work are:

a. To propose a test statistic with a finite sample distribution (under normality assumptions), whereas many existing tests have asymptotic distributions and require simulations to detect their performance in small samples,

b. To make inference by defining and testing a parameter that equivalently reproduces the set of hypotheses on a covariance matrix. The defined parameter bypasses boundary value problem that typically precludes use of tests based on chi-square statistics,

c. To avoid estimating and testing the covariance matrix. As known, the estimation problem is closely related to difficulties of determining how to deal with a non positive definite covariance matrix of random effects during numerical implementation,

d. To define a test in unbalanced models.

Keywords: Covariance Matrix; Unbalanced Linear Mixed Models; Hypotheis testing; Exact test

Abbreviations: LRM: Linear Regression Model; LMM: Linear mixed model

Introduction

An important practical problem is how to discriminate between a linear regression model and a linear mixed model. In order to address the issue of which model is more suitable, one might use standard model selection measures based on information criteria. These approaches are based on the choice of models that minimize an estimate of a specific criterion which usually involves a trade-off between the closeness of the fit to the data and the complexity of the model. We refer to the paper of Muller et al. [1] for a review of these approaches. The paper also gives an overview of the limits and most important findings of the approaches, extracting information from some published simulation results. As is known, one of the major drawbacks of these approaches is that they fail to give any measure of the degree of uncertainty of the model chosen. The value they produce does not mean anything by itself.

Alternatively, because model selection is closely related to hypothesis testing, the choice between a linear regression model (LRM) and a linear mixed model (LMM) could be conducted considering a formal hypothesis test. Noting that models are nested, it is natural to consider the likelihood ratio test. However, the difficulty with this is that it makes the usual approach of comparing the likelihood ratio test statistic with the chi-square distribution inappropriate. The question of whether the variance of a component is zero depends on whether said variance takes its value on the boundary of the parameter space. This situation is known as "non-standard" in relation to the other uses of the likelihood ratio test. For more details see, for example, Self and Liang [2], Stram & Lee [3], Giampaoli & Singer [4]. Comparing the likelihood ratio statistic with the critical value from a chi- square sampling distribution tends not to reject the null as often as it should. Other tests not based on the likelihood function can be implemented (Silvapulle & Sen) [5] but their validity should be carefully detected when applied to unbalanced linear mixed models. All these tests are only valid asymptotically. Finite sample distributions of the likelihood ratio test require simulations and are only reported in particular cases.

When we extend the analysis to multiple variance components, the complexity and difficulties increase. In these cases we have to consider variance covariance matrices and the problem of testing the equality of two positive definite matrices. Hypothesis testing approaches based on the equality of two positive definite matrices have a distinguished history in multivariate statistics. In most cases the likelihood ratio approach is used and the resulting test statistics involve the ratio of the determinant of the sample covariance matrix under the null hypothesis and the alternative hypothesis. Some researchers studied tests based on the trace of two covariance matrices. Roy [6], Pillai [7], Pillai & Jayachandran [8], develop trace-based tests and compare their performance to that of determinant-based tests. The trace test proposed by Pillai is the basis of the test proposed in our work. Denote with s_b the sample covariance matrix of the ordinary least square estimators. Let 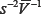be an estimate of the inverse of the (mean of) covariance matrices of the ordinary least square estimators when data come from an LRM (S² is an estimate of the variance of the error term) . Then, given the statistical properties of S_b statistical properties of S_b (Gumpertz & Pantula [9]), we define a test statistic based on a scaled trace of the product of these two matrices. The test has an exact distribution under the null and alternative hypotheses; its expected value is proportional 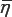to a mean of eigenvalues of the covariance matrix Ω scaled by σ² . Moreover, the application of the test does not involve an estimation Ω of and it works both for balanced and unbalanced linear mixed models.

Conclusion

The complexity of the analysis of multiple variance This work is licensed under Creative components in an LMM is tackled defining a test statistic based on the equality of two appropriate matrices. The test proposed has some features:

a. It has exact distribution under the null and alternative hypotheses.

b. The expected value is proportional to 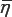a mean of eigenvalues of Ω scaled by σ² . We show that 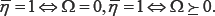. This equivalence allows to bypass the "non standard" problem and to conduct a possible analysis of the power of the test.