Biostatistics and Biometrics Open Access Journal

Research Article

Zero-Truncated Poisson-Garima Distribution and its Applications

Rama Shanker* and Kamlesh Kumar Shukla

Department of Statistics, Eritrea Institute of Technology, Eritrea

Submission: August 23, 2017; Published: September 26, 2017

*Corresponding author: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea, Email: [email protected]; [email protected]

How to cite this article: Rama S, Kamlesh K S . Zero-Truncated Poisson-Garima Distribution and its Applications. Biostat Biometrics Open Acc J. 2017; 3(1): 555605. DOI: 10.19080/BBOAJ.2017.03.555605

Abstract

'In this paper, a zero-truncated Poisson-Garima distribution (ZTPGD) has been introduced by taking the zero-truncated version of Pois- son-Garima distribution (PGD) of shanker [1]. The moments about origin and moments about mean, coefficients of variation, skewness and kurtosis, and index of dispersion of ZTPGD have been obtained. The method of moment and the method of maximum likelihood estimation have been discussed for estimating the parameter of ZTPGD. Goodness of fit of ZTPGD has been discussed with two real data sets and the fit has been compared with that of zero-truncated Poisson distribution (ZTPD) and zero-truncated Poisson-Lindley distribution (ZTPLD).

Abbreviations: ZTPGD: zero-truncated Poisson-Garima distribution; PGD: Poisson-Garima distribution; ZTPD: zero-truncated Poisson distribution; ZTPLD: zero-truncated Poisson-Lindley distribution

Introduction

Suppose P₀ (x; θ) is the original discrete distribution. Then, the zero-truncated version of P₀ (x;θ) is defined as

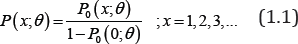
In probability theory, zero-truncated distributions are certain discrete distributions whose support is the set of positive integers. When the data to be modeled originate from a mechanism which generates data that structurally excludes zero counts, zero-truncated distribution is the appropriate choice.

The probability mass function (p.m.f.) of the Poisson-Garima distribution (PGD) given by

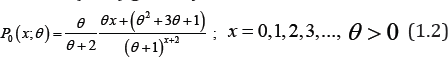
was introduced by shanker [1] to model count data. This distribution arises from the Poisson distribution when its parameter follows Garima distribution introduced by shanker [2] with the probability density function

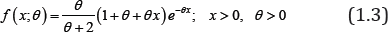
This distribution has been extensively studied by Shanker [2] and it has been shown that (1.3) provides a better model for behavioral science data than many one parameter exponential, Lindley distribution introduced by Lindley[3], Shanker, Akash, Aradhana and Sujatha distributions introduced by [3-7].

In the present paper an attempt has been made to obtain a zero-truncated Poisson-Garima distribution (ZTPGD) by taking the zero-truncated version of Poisson-Garima distribution (PGD) of shanker [1]. Its moments and moments based properties including coefficients of variation, skewness and kurtosis, and index of dispersion of ZTPGD have been obtained and discussed graphically. For estimating the parameter the method of moment and the method of maximum likelihood estimation have been discussed. Goodness of fit of ZTPGD has been discussed with two real data sets and the fit has been compared with that of zero-truncated Poisson distribution (ZTPD) and zero-truncated Poisson-Lindley distribution (ZTPLD) [8].

F (ZTPGD)

Using (1.1) and (1.2), the p.m.f of zero-truncated Poisson- Garima distribution (ZTPGD) can be obtained as

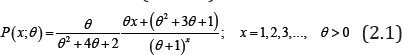
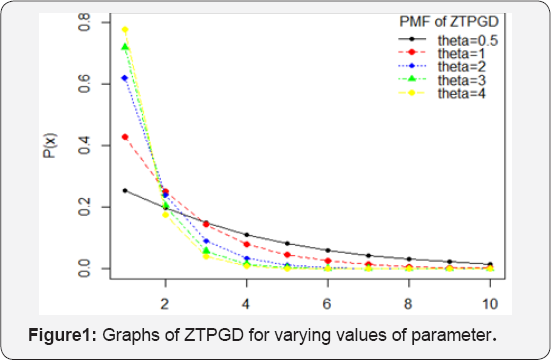
Graphs of ZTPGD for varying values of parameter have been presented in Figure 1. It is clear from the graphs of ZTPGD that as the value of parameter increases, initially graph shift upward and as the value of increases graph decrease fast and becomes asymptote to the x-axis.

The ZTPGD can also be obtained from the size-biased Poisson distribution (SBPD) with p.m.f

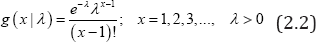
when its parameter follows a continuous distribution having p.d.f.

The pmf of zero-truncated Poisson-Lindley distribution (ZTPLD) obtained by Ghitany et al. [9] is given by

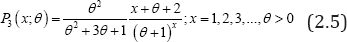
Recall that ZTPLD has been obtained by zero-truncating the discrete Poisson-Lindley distribution suggested by Sankaran [10] and the discrete Poisson-Lindley distribution is the Poisson mixture of Lindley distribution introduced by Lindley [3]. Shanker & Hagos [11] have detailed study on applications of Poisson-Lindley distribution for biological sciences. Shanker et al. [12] have detailed study on modeling of lifetime data using both exponential and Lindley distributions and concluded that both exponential and Lindley distributions compete each other.

The pmf of zero-truncated Poisson distribution (ZTPD) is given by

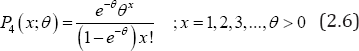
Moments and Related Measures

Using (2.4), the th factorial moment about origin of ZTPGD (2.1) can be obtained as

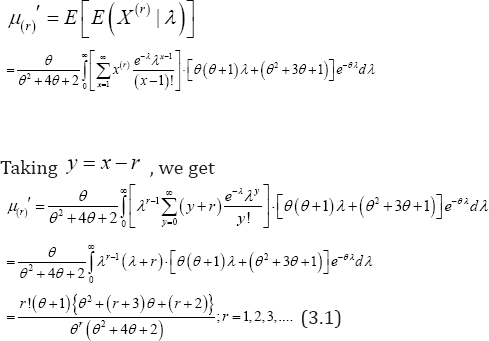
Substituting in (3.1), the first four factorial moments can be obtained and using the relationship between moments about origin and factorial moments about origin, the first four moments about origin of ZTPGD can be obtained as

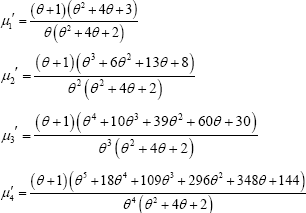
Using the relationship between moments about mean and moments about origin, the first four moments about mean of ZTPGD are thus obtained as

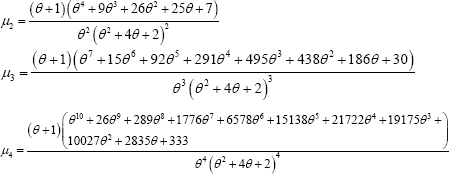
The coefficient of variation (C.V), coefficient of Skewness (√β₁ ) , coefficient of Kurtosis (β₂ ) , and index of dispersion of (γ) ZTPGD are thus obtained as

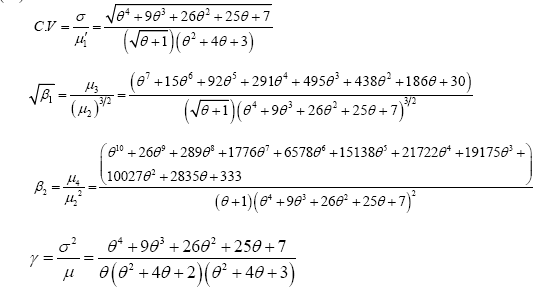
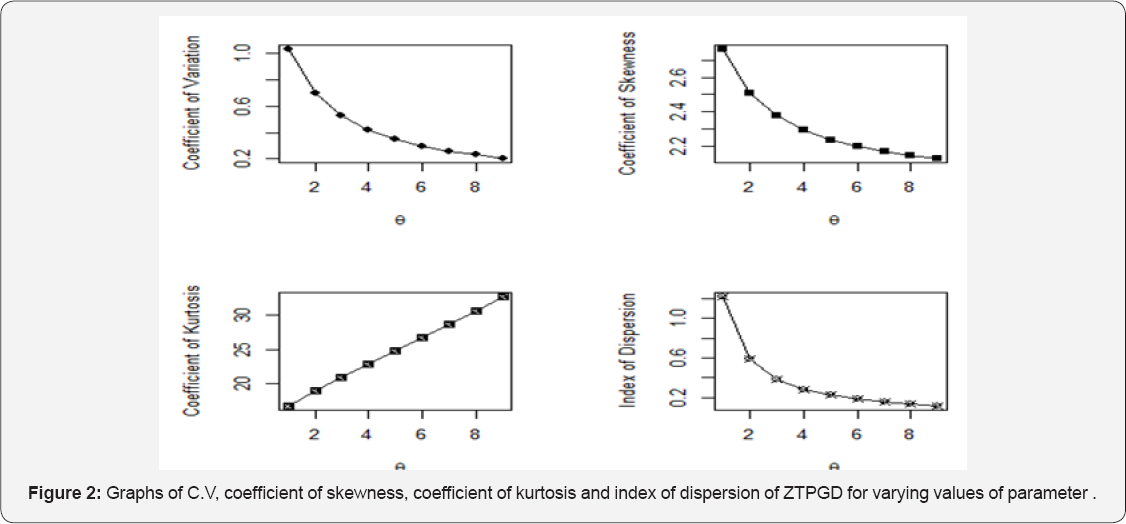
Graphs of C.V, coefficient of skewness, coefficient of kurtosis and index of dispersion of ZTPGD are shown in Figure 2. From the graphs it is obvious that C.V, coefficient of skewness and index of dispersion are increasing while graph of coefficient of kurtosis are increasing for increasing values of the parameter θ

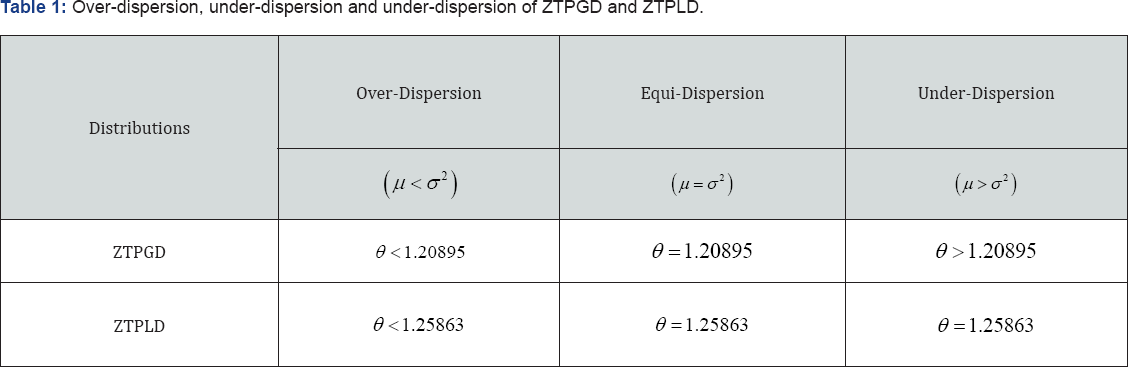
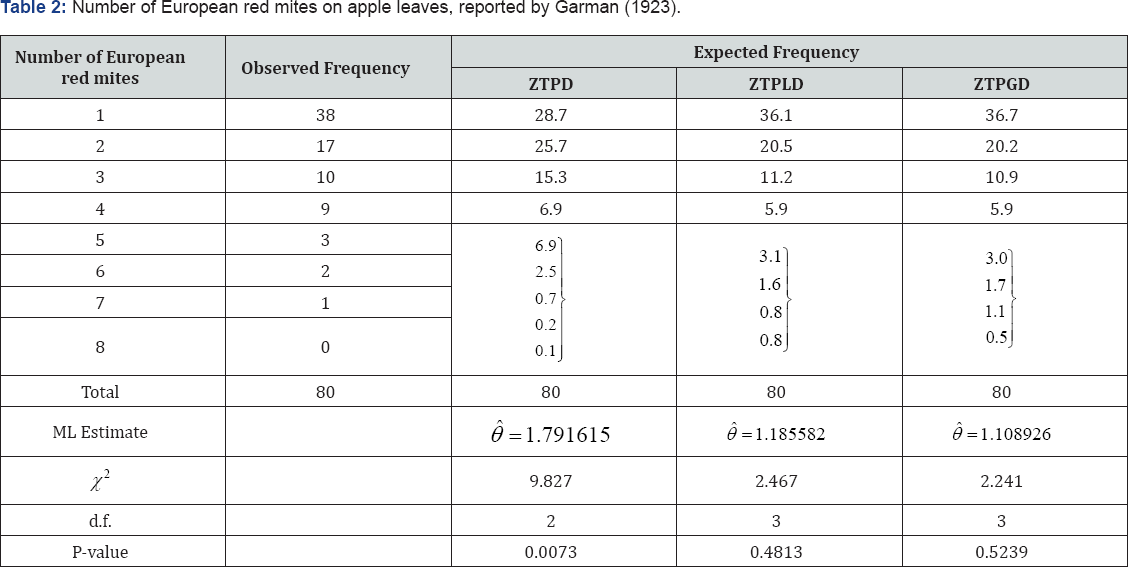
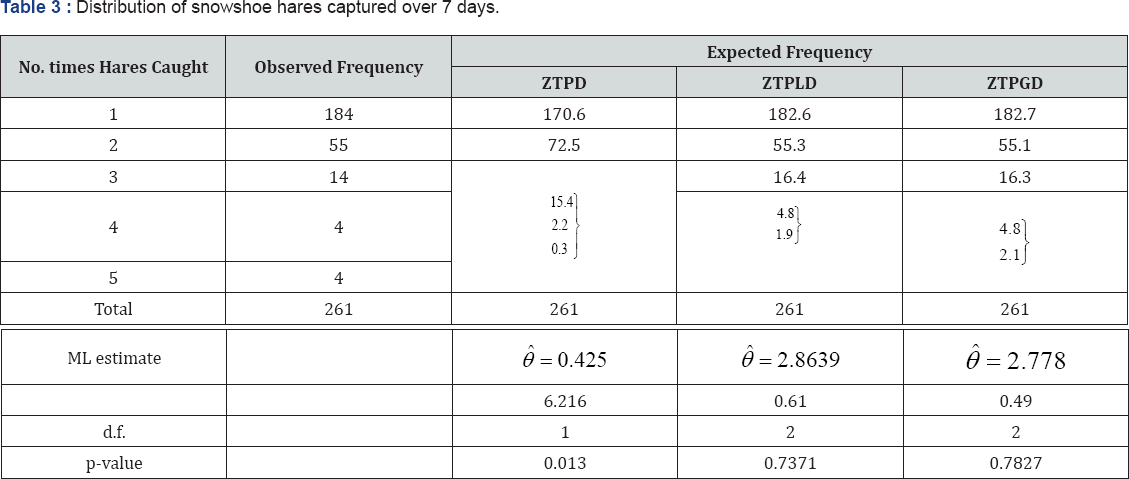
The over-dispersion, under-dispersion and under-dispersionof ZTPGD and ZTPLD for values of parameter are presented in Table 1.

Unimodality and Increasing Hazard Rate: Since

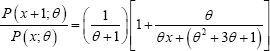
is a decreasing function of , is log-concave. Therefore, ZTPGD is unimodal, has increasing failure rate (IFR), and hence increasing failure rate average (IFRA). It is new better than used (NBU), new better than used in expectation (NBUE), and has decreasing mean residual life (DMRL). Detailed discussions about the definitions of these aging concepts are available in Barlow & Proschan [13].

Generating Function

Probability Generating Function: The probability generating function of the ZTPGD (2.1) is obtained as

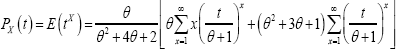
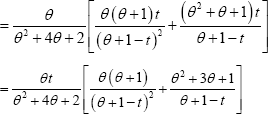
Moment Generating Function: The moment generating function of the ZTPGD (2.1) is given by

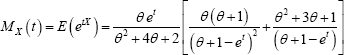
Parameter Estimation

Method of Moment Estimate (MOME)

Let be a random sample of size from the ZTPGD (2.1). Equating the population mean to the corresponding sample mean, MOME of is the solution of the following non-linear equation

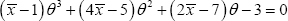
Maximum Likelihood Estimate (MLE)

Let x₁,x₂,...,x_n be a random sample of size from the ZTPGD (2.1) and let f_x be the observed frequency in the sample corresponding to X = x(x = 1,2,3,...,k) such that where is the largest observed value having non-zero frequency The likelihood function of the ZTPGD (2.1) is given by

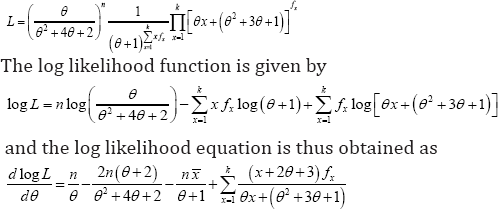
The maximum likelihood estimate 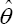of θ is the solution of the equation 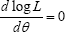and is given by the solution of the following non-linear equation

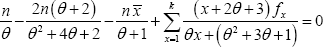
where is the sample mean. This non-linear equation can be solved by any numerical iteration methods such as Newton- Raphson method, Bisection method, Regula-Falsi method etc. The initial value of the parameter can be taken from the value of obtained by the method of moments.

Applications

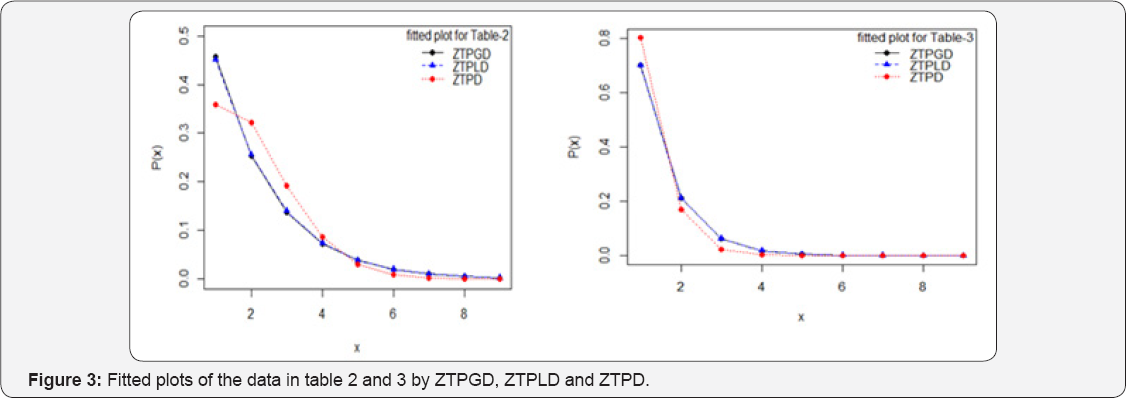
The ZTPGD has been fitted to a number of data - sets to test its goodness of fit over ZTPD and ZTPLD. The maximum likelihood estimate (MLE) has been used to fit the ZTPGD. Two examples of observed data-sets, for which the ZTPD, ZTPLD and ZTPGD has been fitted, are presented. The first data-set in Table 2 is the number of European red mites on apple leaves, reported by Garman [14] and the second data-set in Table 3 is the animal abundance data of Keith & Meslow [15] regarding the distribution of snowshoe hares captured over 7 days ( Figure 3).

Concluding Remarks

A zero-truncated Poisson-Garima distribution (ZTPGD) has been introduced by taking the zero-truncated version of Poisson- Garima distribution (PGD) of Shanker [1]. To find the moments of the distribution ZTPGD has also been obtained by taking a size-biased mixture of an assumed continuous distribution. Its raw moments and central moments and moments based properties including coefficients of variation, skewness and kurtosis, and index of dispersion have been obtained and discussed graphically. Both the method of moment and the method of maximum likelihood estimation have been discussed for estimating the parameter. Finally two examples of real data sets have been presented to test the goodness of fit of ZTPGD and the fit shows quite satisfactory fit over ZTPD and ZTPL