Clinical Image

The Normal Distribution Theorem of Prime Numbers

YinYue Sha*

Dongling Engineering Center, Ningbo Institute of Technology, China

Submission: August 23, 2017; Published: September 20, 2017

*Corresponding author: YinYue Sha, Dongling Engineering Center, Ningbo Institute of Technology, China, Email: shayinyue@qq.com

How to cite this article: YinYue S. The Normal Distribution Theorem of Prime Numbers. Biostat Biometrics Open Acc J. 2017; 3(1): 555601. DOI: 10.19080/BBOAJ.2017.03.555601

key words:

key words: Prime Number; Sieve Method; Prime Number Theorem; Normal Distribution

Introduction

Let Pi (N) be the number of primes less than or equal to N, Pi (2 ≤ Pi ≤ Pm) be taken over the primes less than or equal to √n, then exists the formula as follows:

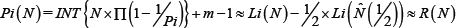
Where the INT { } expresses the taking integer operation of formula spread out type in { }.

One: The Prime Numbers

Let Ni is a natural integer less than or equal to N, then exists the formula as follows: Ni ≤ N (1)

In terms of the above formula we can obtain the array as follows:

(1), (2), (3), (4), (5),.....,(N).

From the above arrangement we can obtain the formula as follows:

Ni(N) = N = Total of integers Ni less than or equal to N (2)

If Ni can be divided by the prime anyone less than or equal to ,√N , then sieves out the positive integer Ni; If Np can not be divided by all primes less than or equal to √N , then the number Np is a prime (Figure 1).

Two: The Sieve Method

Let Pi be a prime less than or equal to √n, the number of integers Ni can be divided by the prime Pi is INT (N / Pi) , the number of integers Ni can not be divided by the prime Pi is:

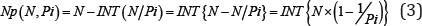
Where the expresses the taking integer operation of formula spread out type in { }.

Three: The Prime Number Theorem

LetPi (N) be the number of primes less than or equal to N, Pi (2 ≤ Pi ≤ Pm) be taken over the primes less than or equal to √N, then exists the formulas as follows:

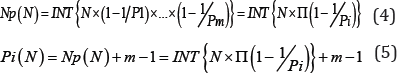
Where the INT { } expresses the taking integer operation of formula spread out type in { }.

Four: The Normal Distribution Theorem of the Prime Numbers

From above we can obtain that:

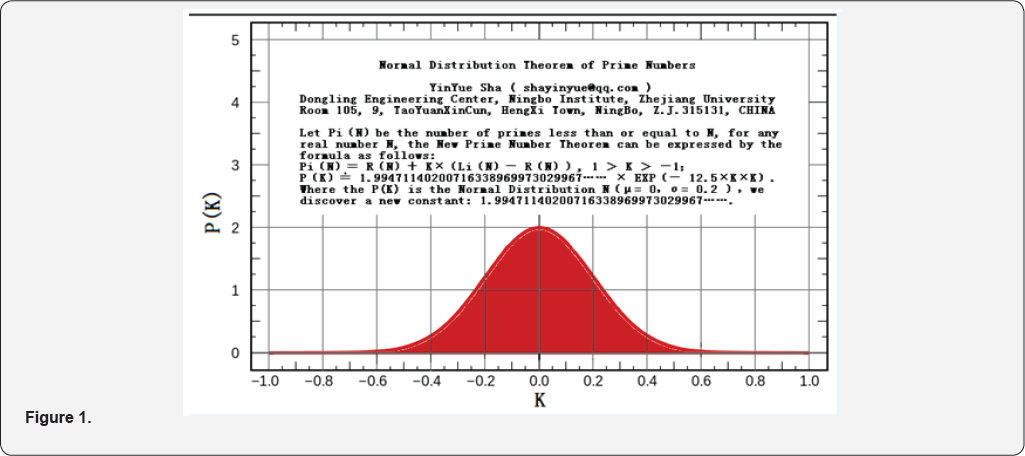
Let Pi (N) be the number of primes less than or equal to N, for any real number N, the New Prime Number Theorem can be expressed by the formulas as follows:

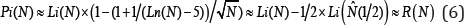
Where Li ( N ) is the logarithmic integral function, the Li ( n ) denotes the natural logarithm of N.

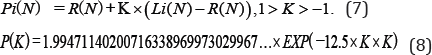
Where the R (N) is the Riemann Prime Counting Function, the R ( n ) is the logarithmic integral function, the p ( k ) is the Normal Distribution N (μ=0,σ=0.2).