Recent Developments on Drawing of Multi-Digit Random Numbers from Single Table of Random TwoDigit Numbers and of Random Three-Digit Numbers
Dhritikesh C*
Department of Statistics, Handique Girls' College, India
Submission: May 22, 2017; Published: August 17, 2017
*Corresponding author: Dhritikesh Chakrabarty, Department of Statistics, Handique Girls' College, India; Email: dhritikesh.c@rediffmail.com; dhritikeshchakrabarty@gmail.com
How to cite this article: Dhritikesh C. Recent Developments on Drawing of Multi-Digit Random Numbers from Single Table of Random Two-Digit Numbers and of Random Three-Digit Numbers. Biostat Biometrics Open Acc J. 2017;2(5): 555597. DOI: 10.19080/BBOAJ.2017.02.555597.
Abstract
Recently, a lot of studies have been done on (i) the construction of tables of random two-digit numbers & random three-digit numbers and (ii) searching for methods of drawing of m-digit random numbers (m > 4) from a single table of random two-digit numbers and/or a single table of random three-digit numbers and/or from a combination of the two which one is suitable. This paper describes a brief review of the findings of these studies
Keywords: Table of random two-digit numbers; Table of random three-digit numbers; Random multi-digit numbers; Method of drawing
Introduction
There had been lot of researches on the construction of tables of random numbers by reputed researchers like Tippett[1] , Mahalanobis [2], Kendall & Smith [3], Fisher & Yates [4], Hald [5], Royo & Ferrer [6], RAND Corporation [7], Quenouille [8], Moses & Oakford [9], Rao, Mitra & Matthai [10], Snedecor and Cochran [11], Rohlf & Sokal [12], Manfred [13], Hill & Hill[14] and others. Among these tables, the following four tables are treated as suitable in drawing of simple random sample (with or without replacement) from a population: The tables of random numbers that had been constructed are of two-digit numbers, three-digit numbers and four-digit numbers only. No table of random m-digit numbers is available till now for m > 5. In the mean time, some studies have been done on testing of the degree of randomness of tables of random numbers due to Tippett, Fisher & Yates, Kendall & Smith and RAND Corporation[15] , Sarmah & Chakrabarty [16 -25] where the said randomness has been found questionable.
Due to this, research has been done on the construction of random two-digit numbers and of random three-digit numbers [26-29]. However, no table of random m-digit numbers is available till now for m > 5. But, there is or there may be necessity of drawing of random five-digit numbers, random four-digit numbers, random seven-digit numbers etc. However, due to the increasing difficulties in the construction of tables of these types of random numbers, it had been compelled to think of an alternative approach of drawing of these types of random numbers. Chakrabarty [30] has already developed methods of drawing of random four-digit numbers & random six-digit numbers from a combination of independent tables of random two-digit numbers & random three-digit numbers [30-32]. In this method of drawing of random four-digit numbers, two independent tables of random two-digit numbers are required. On the other hand, two independent tables of random threedigit numbers are necessary for drawing of random six-digit numbers by the method composed by Chakrabarty [29] while three independent tables of random two-digit numbers are necessary for drawing of the same by the method composed by Chakrabarty [30].
Due to this reason, some studies have been made on In the current study, attempt has been done on searching for methods of drawing of m-digit random numbers (m > 4) from a single table of random two-digit numbers and/or a single table of random three-digit numbers and/or from a combination of the two which one is suitable [33-39]. This paper describes a brief review of (i) the construction of tables of random two-digit numbers & random three-digit numbers and (ii) searching for methods of drawing of m-digit random numbers (m > 4) from a single table of random two-digit numbers and/or a single table of random three-digit numbers and/or from a combination of the two which one is suitable.
Construction of table of random two-digit numbers
Method of construction of a set/table of random occurrences of each of the 100 two-digit numbers
00, 01, 02,........., 98, 99 and also of the 1000 threedigit numbers 000, 001, 002,........, 998, 999 has beendeveloped by Chakrabarty [30]. While constructing a table of random two-digit numbers one is required to note that the table will be random if and only if each of the 100 two-digit numbers occurs n times out of 100n trials (n = 1, 2,.......) in the theoretically ideal situation and the number of occurrence of each of them lies between (n + a % of n) and (n- a % of n) in the practically ideal situation. Let us take a opaque container and 100 small identical balls identifying them by the 100 two-digit numbers as mentioned above. Let the 100 balls be put inside the container and make the balls well shuffled.
If the 100 balls are drawn one by one, by applying the principle of blinding, from the container and the numbers appeared on the balls are listed in the order of their occurrences then 100 observations will be obtained where each of the 100 two-digit numbers will appear once. If the process is repeated and the observations obtained are combined with the earlier ones then 200 observations will be obtained where each of the 100 two-digit numbers will appear twice. If the process is continued, 100n observations will be obtained where each of the 100 two-digit numbers will appear n times out of n repetitions (n = 1, 2, 3, 4 ).
In this experiment, it is found that
(i) each of the 100 numbers occurs n times out of 100n trials (n = 1, 2, 3, 4, ) if we start counting from the (100n + 1)th position
(ii) the number of occurrence of each of them lies between n + 1 if we start counting from any position.
Therefore, the set/table of the observations obtained above will be a random numbers' set/table of the 100 two-digit numbers at ALOCE 0.01.
By this method two tables have been constructed, in 2013 & in 2016 respectively, for random occurrences of the 100 twodigit numbers.
Features of the tables of random two-digit numbers
(1) In each of the two tables, each of the 100 two-digit numbers occurs n times out of 100n consecutive occurrences(n = 1, 2,.......) if we start counting from the observation at the (100k + 1)th position (k = 0, 1, 2, 3,.......).
(2) In each of the two tables, the frequency of occurrence of each of the 100 two-digit numbers out of 100n consecutive trials (n = 1, 2, 3,........ ) may be one more or less than n if we start counting from any position.
(3) The two tables can be treated as random as per the philosophy behind the two definitions of probability namely definition in theoretically ideal situation & and definition in practically ideal situation [39,40].
(4) Each of the two tables is random with respect to the occurrences of the numbers row-wise but not columnwise. Thus while drawing random numbers from the tables; one requires moving row-wise either to the right or to the left starting from any position in the table. The starting position and the direction of movement are to be selected at random by suitable randomized trials in order to keep their randomness intact.
Method of drawing of random two-digit numbers
Each of the two independent tables of random two-digit numbers, constructed here, can be used in drawing of random two-digit numbers which are distinct and (2) which are not necessarily distinct.
Drawing of distinct random two-digit numbers: Suppose that we want to draw n random two-digit numbers from the table constructed by Chakrabarty in 2016 [27]. Here, this table will be identified as Table-1 such that the drawn numbers are distinct. Since distinct two-digit numbers are to be drawn, one can draw a maximum of 100 such numbers since the total number of twodigit numbers is 100. Feature no (2) mentioned in section 2.3.1 implies that if n two-digit numbers occurred consecutively from the (100k + 1)th position (k = 0, 1, 2, ........) in the table are drawn subject to the feature no (4) then the drawn n numbers will be distinct and random. Also, feature no (3) mentioned in section 2.3.1 implies that if n two-digit numbers occurred consecutively in the table are drawn starting from any position then the drawn n numbers may not be distinct. Some of them may occur twice. Thus in order to draw distinct numbers, it is required to exclude the next occurrence(s) of the same number and to draw the next consecutive number(s) occurred in the table following feature no (4).
Thus the drawing of random two-digit numbers consists of the two basic tasks namely (a) selection of the starting position at random and (b) selection of the direction (right or left) of movement at random.
Accordingly, in order to obtain the n random two-digit numbers one is to proceed with the following steps:
(1) Select the position, from where one will have to start the drawing of the numbers, at random. Since the table contains 10000 random occurrences of the 100 two-digit numbers, there are 10000 positions of the numbers namely 0000, 0001, 0002, ........,9999.
In selecting the starting position, one thus can apply some usual manual randomization technique of drawing one number from among the numbers 0000, 0001, 0002,......, 9999.
One method of drawing of such number is as follows:
Take a set of 10 identical small balls distinguishing them by marking with the 10 digits
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and put them inside a opaque container, say C1.
Similarly, take another set of 4 identical small distinguishing them by marking L, R, M1, M2 respectively and another opaque container, say C2. Now, draw one ball at random from the container C1 containing the 10 balls and note down digit appeared on it. Let the digit is d1. Next, draw another ball at random from the container C1 containing the same 10 balls and note down digit appeared on it. Let the digit be d2.
Then, draw one ball at random from the container C2 putting 2 balls marked with L & R inside it.
If the drawn ball is R then put the digit d2 at the right position of d1 and if the drawn ball is L then put the digit d2 at the left position of d1. Thus if the ball R appears then the selected twodigit number will be d1 d2 and if the ball L appears then the selected two-digit number will be d2 d1. Let the selected twodigit number be d2 d1. Next, draw another ball at random from the container C1 containing all the 10 balls and note down digit appeared on it. Let the digit be d3. Then, draw one ball at random from the container C2 putting 3 balls marked with L, M1 & R inside it and put the digit d3 at the left position of d2 d1. if the drawn ball is L, the middle position of d2 d1. if the drawn ball is M1 & the right position of d2 d1. if the drawn ball is R. Thus the selected three-digit number will be d3d2 d1 or d2d3 d1 or d2d1 d3 in accordance with the selected ball is L or M1 or R. Let the selected three-digit number be d3d2 d1.
Finally, draw another ball at random from the container C1 containing all the 10 balls and note down digit appeared on it. Let the digit be d4. Then, draw one ball at random from the container C2 putting 4 balls marked with L, M1, M2 & R inside it and put the digit d4 at the left position of d2d3d1 if the drawn ball is L, the 1st middle position (from left) of d2d3 d1 if the drawn ball is M1, the 2nd middle position (from left) of d2d3 d1 if the drawn ball is M2& the right position of d2d3 d1 if the drawn ball is R.
Thus the selected four-digit number will be
d4d3 d2d1 or d2d4 d3d1 or d2d1 d4d3 or d2d1 d3d4 in accordance with the selected ball is L or M1 or M2 or R. This selected number will be the required starting position.
(2) Let the ith position be selected as the starting position. Draw the number that occurs at the ith position in the table.
(3) Chose whether to move towards left or towards right. The choice can be made at random by performing a random binary trial (for example, by tossing of an unbiased coin or by drawing a number from the container C2 putting two identical balls, marked with L and R respectively, inside it.
(4) If it is chosen to move towards right, draw the numbers occurred at the positions i, i + 1, i + 2,....., i + n- 1in the table to obtain the n random two-digit numbers.
(5) If it is chosen to move towards left, draw the numbers occurred at the positions i, i - 1, i - 2,...., i - n + 1in the table to obtain the n random two-digit numbers.
(6) It may occur that some number or numbers among those drawn may be occurred twice. In that situation, retain only one occurrence of them and draw additional numbers appeared at the consecutive positions in the table as per requirement. If k additional numbers are required to draw, then draw the numbers occurred at the positions i + n, i + n + 1, i + n + 2,......, i + n + k - 1 if it is chosen to move towards right and draw the numbers occurred at the positions i - n, i - n - 1, i - n - 2,....., i - n - k + 1 ifit is chosen to move towards left.
Drawing of random two-digit numbers (not necessarily distinct): The features (1) and (2) in section 2.1 imply that if two-digit numbers are picked up at a gap of g positions (101 < g < 199), the picked up numbers will not necessarily be distinct.
Thus in order to draw n random two-digit numbers which need not necessarily be distinct, one is to proceed with the following steps:
(1) Select one position from where to start at random by the similar method as in the case of drawing of distinct random two-digit numbers mentioned above. Let the ith position be selected.
(2) Draw the number that occurs at the ith position in the table.
(3) Chose the length of jump that is to be 101 or more and 199 or less at random. It can be chosen by some usual manual randomization technique of drawing one number from among the numbers 101, 102, 103,...... , 198, 199.Let the selected length of jump be l. The random selection of the length of the jump can be done by similar method as done in the selection of the starting position.
(4) Chose whether to jump towards left or towards right. The choice can be made by the same method as in the earlier case.
(5) If it is chosen to jump towards right, draw the numbers occurred at the positions i, i + l, i + 2l,....... , i + (n - 1) l in the table to obtain the required n random two-digit numbers.
(6) If it is chosen to move towards left, draw the numbers occurred at the positions i, i- l, i- 2l,......... , i- (n- 1) l in the table to obtain the required n random two-digit numbers.
Example of drawing of random two-digit numbers
Example: 1 (Drawing of distinct random two-digit numbers): Let it be wanted to draw 10 random distinct twodigit numbers from the Table-A. Suppose that the starting position selected at random be 0576. The two-digit number at this position in the table is 20. Thus, this is selected as the 1st one among the tens to be selected. Suppose that it is chosen by random trial to move towards the right direction. Then the numbers at the positions 0577, 0578,....... , 0585 are to be drawn. Now the two-digit numbers at the next 9 positions in the table are 65, 37, 45, 86, 92, 02, 71, 14, 49.
Therefore, the 10 random distinct two-digit numbers will be 20, 65, 37, 45, 86, 92, 02, 71, 14, 49.
Example: 2 (Drawing of random two-digit numbers (Not Necessarily Distinct): Let it be wanted to draw 10 random two-digit numbers from Table-1 which need not necessarily be distinct. Suppose that the starting position selected at random be 9675. The two-digit number at this position in the table is 34. Thus this is selected as the 1st one among the 10 numbers to be selected. Suppose that it is chosen by random trial to move towards the right direction. Let the length of jump selected at random be 105. Then the next 9 positions in the table to be considered (treating the table as circular) will be 9780, 9885, 9990, 0095, 0200, 0305, 0410, 0515,0620. The number appeared at these positions in the table are 41, 93, 46, 42, 10, 72, 96, 52, 27. Accordingly, the 10 random two-digit numbers drawn from the table are 34, 41, 93, 46, 42, 10, 72, 96, 52, 27.
Construction of table of random three-digit numbers
Method of construction of a set/table of random occurrences of the 1000 three-digit numbers is similar to the method of construction of a set/table of random occurrences of the 100 twodigit numbers. The only point is that in this case we are to take a opaque container and 1000 small identical balls identifying them by the 1000 three-digit numbers in place of 1000 small identical balls. By this method two tables have been constructed, in 2013 & in 2016 respectively, for random occurrences of the 1000 three-digit numbers.
Features of the tables of random three-digit Numbers
(1) In each of the two tables, each of the 1000 threedigit numbers occurs n times out of 1000n consecutive occurrences (n = 1, 2, ..... ) if we start counting fromthe observation at the (1000k + 1)th position (k = 0, 1, 2,3 ........).
(2) In each of the two tables, the frequency of occurrence of each of the 1000 three-digit numbers out of 1000n consecutive trials (n = 1, 2 ....) may be one more or less than n if we start counting from any position.
(3) Each of the two tables can be treated as random as per the philosophy behind the two definitions of probability namely definition in theoretically ideal situation and definition in practically ideal situation.
(4) The two tables are random with respect to the occurrences of the numbers row-wise but not columnwise. Thus while drawing random numbers from the table, one requires moving row-wise either to the right or to the left starting from any position in the table. The starting position and the direction of movement are to be selected at random by suitable randomized trials in order to keep their randomness intact.
Method of drawing of random three-digit numbers
Each of the two tables, constructed here, can be used in drawing of random three-digit numbers which are distinct and (2) which are not necessarily distinct.
Drawing of distinct random three-digit numbers:Suppose that we want to draw n random three-digit numbers from the table constructed by Chakrabarty in [28]. Here this table will be identified as Table-2. Since distinct three-digit numbers are to be drawn, one can draw a maximum of 1000 such numbers since the total number of such numbers is 1000. Feature no (2) mentioned in section 3.1 implies that if n threedigit numbers occurred consecutively from the (1000k + 1)th position (k = 0, 1, 2,...... ) in the table are drawn subject to the feature no (4) then the drawn n numbers will be distinct and random. Also, feature no (3) mentioned in the same section implies that if n three-digit numbers occurred consecutively in the table are drawn starting from any position then the drawn n numbers may not be distinct. Some of them may occur twice. Thus in order to draw distinct numbers, it is required to exclude the next occurrence(s) of the same number and to draw the next consecutive number(s) occurred in the table following feature no (4).
Thus the drawing of random three-digit numbers consists of the two basic tasks namely
(a) selection of the starting position at random & (b) selection of the direction (right or left) of movement at random. Accordingly, in order to obtain the n distinct random threedigit numbers one is to proceed with the following steps:
(1) Select the position, from where to start, at random. Since the table contains 10000 random occurrences of the 1000 three-digit numbers, accordingly there are 10000 positions of the numbers namely 0000, 0001, 0002,.......... , 9998,9999. The starting position can be selected by the same method as in the case of drawing of random two-digit numbers.
(2) Let the ith position be selected in the earlier step. Draw the number that occurs at the ith position in the table.
(3) Chose whether to move towards left or towards right. The choice can be made at random by a binary trial e.g. by tossing of an unbiased coin or by drawing a number from the container C2 putting two identical balls, marked with L and R respectively, inside it.
(4) If it is chosen to move towards right, draw the numbers occurred at the positions i, i + 1, i + 2,...... , i + n - 1 in the table to obtain the n random three-digit numbers.
(5) If it is chosen to move towards left, draw the numbers occurred at the positions i, i -1, i - 2,....... , i - n + 1 in the table to obtain the n random three-digit numbers.
(6) It may occur that some number or numbers among those drawn may be occurred twice. In that situation, retain only one occurrence of them and draw additional numbers appeared at the consecutive positions in the table as per requirement.
If k additional numbers are required to draw, then draw the numbers occurred at the positions i + n, i + n + 1,, i + n +2,...... ,i + n + k -1 if it is chosen to move towards right and draw the numbers occurred at the positions i - n, i - n - 1, i - n - 2,...... , i -n - k + 1 if it is chosen to move towards left.
Drawing of random three-digit Numbers (not necessarily distinct): The features (1) and (2) section 3.1 imply that if threedigit numbers are picked up at a gap of g positions (1001 < g < 1999), the picked up numbers will not necessarily be distinct. Thus in order to draw n random two-digit numbers which need not necessarily be distinct, one is to proceed with the following steps:
(1) Select one position from where to start at random by the similar method as in the case of drawing of distinct random two-digit numbers mentioned above. Let the ith position be selected.
(2) Draw the number that occurs at the ith position in the table.
(3) chose the length of jump that is to be 1001 or more and 1999 or less at random. It can be chosen by some usual manual randomization technique of drawing one number from among the numbers 101, 102, 103, , 198, 199.
Let the selected length of jump be l. The random selection of the length of the jump can be done by similar method as done in the selection of the starting position.
(4) Chose whether to jump towards left or towards right. The choice can be made by the same method as in the earlier case.
(5) If it is chosen to jump towards right, draw the numbers occurred at the positions i, i + l, i + 2l, , i + (n - 1) l in the table to obtain the required n random two-digit numbers.
(6) If it is chosen to move towards left, draw the numbers occurred at the positions i, i- l, i- 2l, , i- (n- 1) l in the table to obtain the required n random three-digit numbers.
Example of drawing of random three-digit numbers
Example 1) (Drawing of distinct random three-digit numbers): Let it be wanted to draw 10 random distinct threedigit numbers from Table-2. Suppose that the starting position selected at random be 4592. The three-digit number at this position in Table-2 is 708.Thus this is selected as the 1st one among the ten three-digit numbers to be selected. Suppose that it is chosen by random trial to move towards the right direction. Then the numbers at the positions 4593, 4594, 4595, 4596, 4597, 4598, 4599, 4600, 4601are to be drawn. Now the threedigit numbers at the next 9 positions in Table-1 are 205, 111, 641, 758, 334, 999, 389, 023, 331.Therefore, the 10 random distinct three-digit numbers will be 708, 205, 111, 641, 758, 334, 999, 389, 023, 331.
Example -2 (Drawing of distinct random three-digit numbers): Let it be wanted to draw 20 random distinct threedigit numbers from the same table. Suppose that the starting position selected at random be 9986. The three-digit number at this position in the table is 578.Thus this is selected as the 1st one among the 20 numbers to be selected. Suppose that it is chosen by random trial to move towards the right direction. Then the numbers at the next 19 successive positions are to be selected. However, after 13 positions, the table comes to the end. The remaining 6 positions are then taken from the beginning of the table treating the table to be a circular one.
Thus the 19 three-digit numbers at the next 19 successive positions in the table are151, 652, 088, 596, 411, 453, 597, 011, 667, 796, 129, 741, 250, 439,710, 450, 940, 181, 913.
Accordingly, the 20 random three-digit numbers drawn from the table are578, 151, 652, 088, 596, 411, 453, 597, 011, 667, 796, 129, 741, 250, 439,710, 450, 940, 181, 913.
Example -3 (Drawing of distinct random three-digit numbers (not necessarily distinct): Let it be wanted to draw 10 random three-digit numbers from the same table which need not necessarily be distinct. Suppose that the starting position selected at random be 4510. The three-digit number at this position in the table is 426.Thus this is selected as the 1st one among the 10 numbers to be selected. Suppose that it is chosen by random trial to move towards the right direction. Let the length of jump selected at random be 1010.Then the next 9 positions in the table to be considered (treating the table as circular) will be 5520, 6530, 7540, 8550, 9560, 0570, 1580, 2590, 3600.
The number appeared at these positions in the table are 186, 034, 513, 766, 379, 240, 272, 715, 630.
Accordingly, the 10 random three-digit numbers drawn from the table are426, 186, 034, 513, 766, 379, 240, 272, 715, 630.
Method of Drawing of Random m-Digit Numbers (m > 5)
Now, discussion will be made on the methods of drawing of random m-digit numbers (for m = 4, 5, 6, 7, 8, 9).
Drawing of random four-digit numbers: Let d1d2 be a two-digit number drawn from the table of random two-digit numbers. The possible values that d1d2 assumes are the 100 two-digit numbers 00, 01, 02 ...... , 98, 99 and the probability that d1d2 assumes any of them is equal which is 0.01. Similarly, if d3d4 is another two-digit number drawn independently from the same table then the possible values that d3d4 assumes are also the same 100 two-digit numbers and the probability that that d3d4 assumes any of them is equal which is 0.01. Now if the two two-digit numbers namely d1d2 & d3d4 are combined together to form the four-digit number d1d2d3d4 then the possible values that d1d2d3d4 assumes are the 10000 four-digit numbers;
0000, 0001, 0002,........ , 9998, 9999and the probability that d1d2d3d4 assumes any one of them is equal which is 0.0001 (since the two numbers d1d2 & d3d4 have been drawn independently). Thus the four-digit number d1d2d3d4 is a random one. Similarly, the other four-digit number d1d2d3d4 is also a random one.
If one of these two four-digit numbers is selected by performing a random binomial trial, the selected number will be a random four-digit number. If the process is repeated once, one more random four-digit number can be obtained. By further repetitions, one can obtain more random four-digit numbers. Therefore in order to draw n random four-digit numbers from a single table of random two-digit numbers, it is required to draw two independent sets, each of n random two-digit numbers, from the table. It is to be noted that any successive two digits of different four-digit numbers can be same. Conversely, with the same successive two digits there can be different four-digit numbers. Therefore, the random two-digit numbers in each of the two independent sets of random two-digit numbers, drawn in order to form random four-digit numbers, not necessarily be distinct.
It is further to be noted that the random selection of which set's two-digit numbers will be placed at the left position, which set’s two-digit number will be placed at the right position while combining them in the formation of random four-digit number can be made afresh for each random four-digit number to be drawn or can be made once, before drawing the two-digit numbers for the two sets, to be applied in the construction of all random four-digit numbers to be selected. Thus, in order to draw n random four-digit numbers one can apply the following two methods
First method of drawing
In order to draw n random four-digit numbers, in this method, one can proceed with the following steps:
(1) Make a choice at random which set's two-digit numbers will be placed at the left position and which set’s two-digit number will be placed at the right position while combining them in the formation of random four-digit numbers. This can be done by a binomial trial.
(2) Draw the 1st set of n random two-digit number from the table by the method discussed in Section II b.
(3) Draw the 2nd set of n random two-digit number from the table by the same method independently from the 1st set.
(4) Combine the random two-digit numbers of the 1st set with the corresponding random two-digit numbers of the 2nd set by the choice of the positions obtained in step (1) to obtain the n random four-digit numbers.
Second method of drawing
In order to draw n random four-digit numbers, in this method, one can proceed with the following steps:
(1) Draw two random two-digit numbers independently from the table of random two-digit numbers by the same method as discussed in Section II b.
(2) Make a choice at random which set's two-digit numbers will be placed at the left position and which set’s two-digit number will be placed at the right position while combining them in the formation of random four-digit numbers. This can be done by a binomial trial.
(3) Combine the two two-digit numbers, obtained in step(1) , as per the selected choice of the positions to obtain one random four-digit number.
(4) Perform the above three steps more (n-1) times to obtain more (n-1) random four-digit numbers.
(5) The random four-digit numbers obtained in step (3) & Step (4) are the required n random four-digit numbers.
Example -1 (Drawing of random four-digit numbers)
Let it be wanted to draw 20 random four-digit numbers.
Let us take the table of random two-digit numbers.
First method of drawing
Let a trial namely the throwing of an unbiased coin be performed to make a choice which set’s two-digit number will be placed at the left position and which set's two-digit number will be placed at the right position while combining them in the formation of random four-digit number.
Suppose, the selected choice is as follows:
Two-digit number belonging to the 1st Set will be placed at the Right position, & Two-digit number belonging to the 2nd Set will be placed at the Left position.
Now let us draw the 1st set of 20 random two-digit numbers from Table-A. Let the numbers drawn be
64, 47, 55, 83, 37, 90, 50, 28, 54, 36, 51, 09, 90, 27, 42, 13,46, 59, 27, 77.
Next, let us draw the 2nd set of 20 random two-digit numbers from the same table independently of the 1st set. Let the numbers drawn, in this case, be
09, 96, 39, 94, 52, 07, 80, 66, 42, 27, 99, 02, 89, 28, 50, 52, 36, 81, 53, 34.
Now, let us combine the corresponding numbers drawn from the two tables as per the selected choice of combination. Thus, the selected 20 random four-digit numbers are
0964, 9647, 3955, 9483, 5237, 0790, 8050, 6628, 4254, 2736, 9951, 0209, 8990, 2827, 5042, 5213, 3646, 8159, 5327, 3477.
Second method of drawing
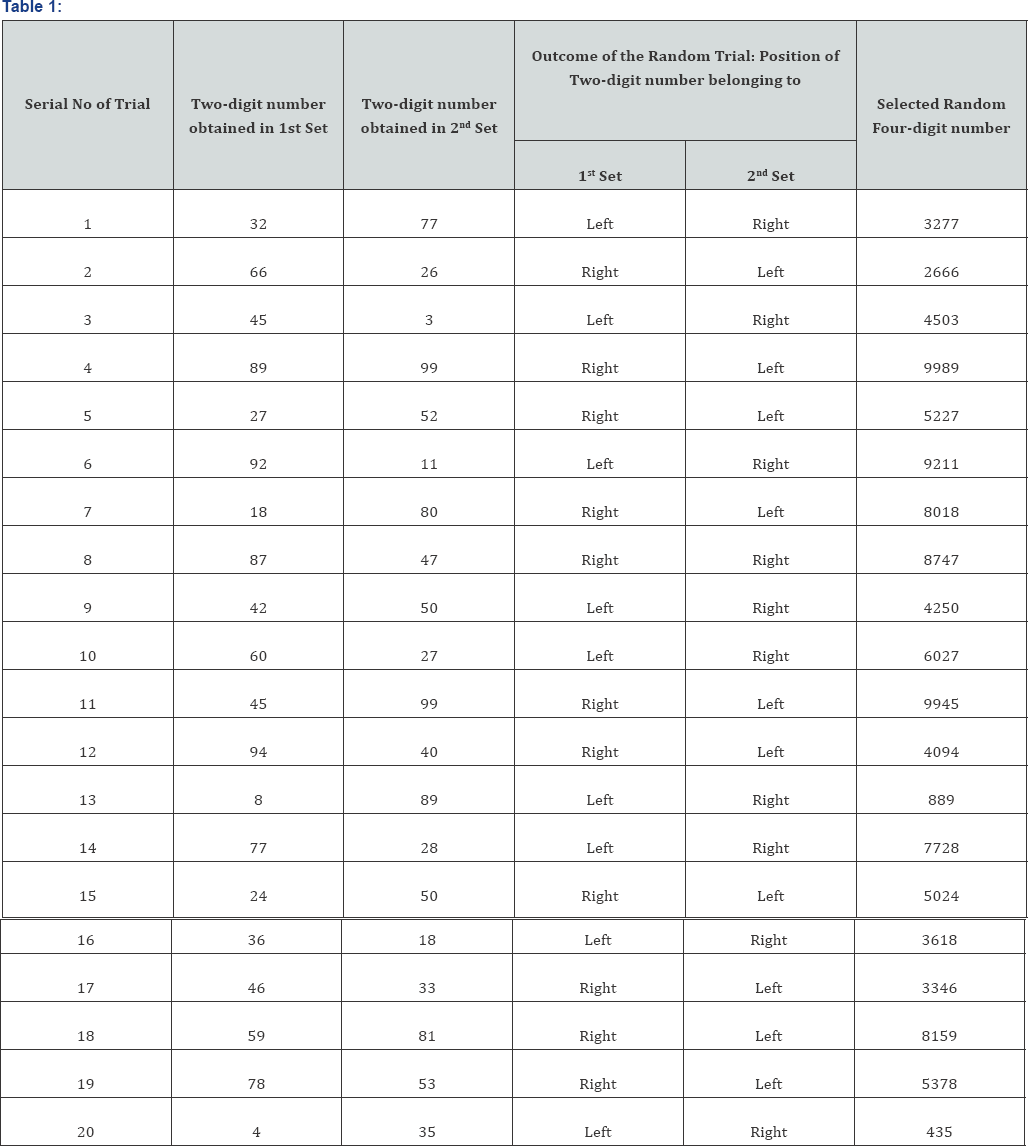
First, let us draw 2 random two-digit numbers independently to include in the two sets namely the 1st Set, & the 2nd Set respectively from Table-1. Let the two numbers drawn be 32 & 77 respectively. Next, let a random binomial trial namely tossing of an unbiased coin be performed to choice which set's two-digit number will be placed at the left position and which set’s two-digit numbers will be placed at the right position while combining them in the formation of random four-digit numbers. Suppose, the selected choice is as follows:
Two-digit number belonging to the 1st Set will be placed at the Left position, & Two-digit number belonging to the 2nd Set will be placed at the Right position. Thus, the 1st selected fourdigit random number is 3277.
In order to obtain the remaining 19 random four-digit numbers, the two steps are to be repeated 19 times.
Let the outcomes of all the 20 trials be as follows (Table 1): Thus, the selected 20 random four-digit numbers to are 3277, 2666, 4503, 9989, 5227, 9211, 8018, 8747,4250, 6027, 9945, 4094, 0889, 7728, 5024, 3618, 3346, 8159, 5378, 0435.
4.3. Drawing of Random Five-Digit Numbers: Let d1d2 & d3d4d5 be two numbers drawn at random from Table Table-1and Table-2 respectively.
By similar logic as in the case of drawing of random four-digit numbers, it is obtained that each of the two five-digit numbers d1d2d3d4d5, d3d4d5d1d2 is random. If one of these two five-digit numbers is selected by performing a binary random trial, the selected number will be a random five-digit number. If the process is repeated once, one more random five-digit number can be obtained. By further repetitions, one can obtain more random five-digit numbers. Thus, in order to draw n random five-digit numbers one can proceed with the following steps:
(1) Make a choice at random whether two-digit numbers will be placed at the left position or three-digit numbers will be placed at the left position while combining them in the formation of random five-digit numbers. This can be done by a binary random trial.
(2) Draw n random two-digit numbers from Table-1
(3) Draw n random three-digit numbers from Table-2.
(4) Combine the random two-digit numbers obtained from Table-1 with the corresponding random three-digit numbers obtained from Table-2, as per the choice of the position obtained in step (1), to obtain the n random fivedigit numbers.
In order to draw n random five-digit numbers one can also proceed with the following steps:
(1) Draw one random two-digit numbers from Table-1.
(2) Draw one random three-digit numbers from Table-2.
(3) Make a choice at random whether two-digit number will be placed at the left position or three-digit number will be placed at the left position while combining them in the formation of random five-digit numbers. This can be done by a binary random trial.
(4) Combine the two numbers as per the selected choice of the positions to obtain one random five-digit number.
(5) Repeat the four steps, from the 2nd step to the 5th step, more (n-1) times to obtain n random five-digit numbers.
Example of drawing of random five-digit numbers:
Example (4.3.1-1): Let it be wanted to draw 10 random five-digit numbers: Let a random binary trial be performed to choice whether two-digit numbers will be placed at the left position or three-digit numbers will be placed at the right position while combining them in the formation of random fivedigit numbers. Let the choice be that two-digit numbers will be placed at the left position. Now let us draw 10 random two-digit numbers (not necessarily distinct) from Table-1. Let the drawn 10 random two-digit numbers be 63, 82, 65, 82, 83, 10, 72, 96, 52, 27. Next let us draw 20 random three-digit numbers from Table-2. Let the drawn 10 random two-digit numbers be 530, 895, 183, 500, 239, 291, 980, 503, 477, 392. Thus the 10 random five-digit numbers to be selected will be 63530, 82895, 65183, 82500, 83239, 10291, 72980, 96503, 52477, 27392
Drawing of random six-digit numbers
There can be two alternative ways of drawing of random sixdigit numbers from the six tables constructed here. These are as follows: By using two tables of random three-digit numbers. By using three tables of random two-digit numbers. Either any two of the three tables of random three-digit numbers or all the three tables of random two-digit numbers can be used in drawing random six-digit numbers.
Drawing of random six-digit numbers from table of random three-digit numbers: Let d 1 d 2 d 3 ,d 4 d 5 d 6be two three digit numbers drawn from the table of the random three-digit numbers independently of each other. By similar logic as in the case of drawing of random four-digit numbers, it is obtained that each of the two six-digit numbers d1d2d3d4d5d6, d4d5d6d1d2d3 is random. If a six-digit number is selected from these two six-digit numbers by performing a binomial trial, the selected number will be a random six-digit number. If the process is repeated once, one more random six-digit number can be obtained. By further repetitions, one can obtain more random six-digit numbers. Therefore in order to draw n random six-digit numbers from the table of random three-digit numbers, it is required to draw two independent sets, each of n random three-digit numbers, from the table. It is to be noted that any successive three digits of different six-digit numbers can be identical. Conversely, with the identical successive three digits there can be different six-digit numbers. Therefore, the random three-digit numbers in each of the two independent sets, drawn in order to form random sixdigit numbers, need not necessarily be distinct.
Thus, in order to draw n random six-digit numbers one can proceed with the following steps:
(1) Make a choice at random which set's three-digit numbers will be placed at the left position and which set's three-digit number will be placed at the right position while combining them in the formation of random six-digit numbers. This can be done by a binary trial that results in two equally likely possible outcomes.
(2) Draw the 1st set of n random three-digit number from Table-2.
(3) Draw the 2nd set of n random three-digit number from the same table independently of the 1st set.
(4) Combine the random three-digit numbers of the 1st set with the corresponding random three-digit numbers of the 2nd set by the choice of the positions obtained in step (1) to obtain the n random six-digit numbers.
In order to draw n random six-digit numbers one can also proceed with the following steps:
(1) Draw two random three-digit numbers independently from Table-2.
(2) Make a choice at random which three-digit number will be placed at the left position and which three-digit number will be placed at the right position while combining them in the formation of random six-digit numbers. This can be done by the binomial trial.
(3) Combine the two three-digit numbers, obtained in step (1) , as per the selected choice of the positions to obtain one random six-digit number.
(4) Perform the above three steps more (n-1) times to obtain more (n-1) random six-digit numbers.
(5) The random six-digit numbers obtained in step (3) &Step (4) are the required n random six-digit numbers.
Example of drawing of random six-digit numbers
Example -1: Let it be wanted to draw 10 random six-digit numbers from Table-1.
Let a binary trial be performed to choice which set’s threedigit numbers will be placed at the left position and which set's three-digit numbers will be placed at the right position while combining them in the formation of random six-digit numbers. Let the 1st set be the choice that the numbers belonging to it will be placed at the left position. Now let us draw the 1st set of 10 random three-digit numbers from Table-2. Let the numbers drawn be
811, 682, 707, 218, 966, 171, 020, 582, 591, 122.
Next let us draw the 2nd set of 10 random three-digit numbers from Table-2 independently of the 1st set. Let the numbers drawn be 789, 908, 801, 031, 798, 507, 317, 870, 754, 050. Thus the 10 random six-digit numbers to be selected will be
789811, 908682, 801707, 031218, 798966, 507171, 317020, 870582, 754591, 050122.
Drawing of random six-digit numbers from table of random two-digit numbers
Let d 1 d 2, d 3 d 4 & d 5 d 6be three two-digit numbers drawn from the table of random two-digit numbers independently of each other. By similar logic as in the case of drawing of random four-digit numbers, it is obtained that each of the six six-digit numbers1 d 2 d 3 d 4 d 5d6 , 1 d 2 d 5 d 6 d 3d4 , 3 d 4 d 1 d 2 d 5d6 , 3 d 4 d 5 d 6 d 1d2 d5d6d1d2d3d4, d5d6d3d4d1d2 is random. If a six-digit number is selected from these six six-digit numbers by performing a random trial consisting of six possible outcomes (for example by throwing of a fair dice), the selected number will be a random six-digit number. If the process is repeated once, one more random six-digit number can be obtained. By further repetitions, one can obtain more random six-digit numbers.
Therefore in order to draw n random six-digit numbers from the table of random two-digit numbers, it is required to draw three independent sets, each of n random two-digit numbers, from the table. It is to be noted that any successive two digits of different six-digit numbers can be same. Conversely, with the same successive two digits there can be different six-digit numbers. Therefore, the random two-digit numbers in each of the three independent sets of random two-digit numbers, drawn in order to form random six-digit numbers, need not necessarily be distinct. Thus, in order to draw n random six-digit numbers from the table of random two-digit numbers one can proceed with the following steps:
(1) Make a choice at random which set's two-digit numbers will be placed at the left position, which set’s two-digit numbers will be placed at the middle position and which set's two-digit numbers will be placed at the right position while combining them in the formation of random six-digit numbers. This can be done by a random trial that results in 6 possible outcomes. Throwing of an unbiased dice, distinguishing its six sides by the six possible outcomes, can be performed in selecting the said choice.
(2) Draw 1st set of n random two-digit number from Table-1.
(3) Draw 2nd set of n random two-digit number from the table by the same steps independently of the 1st set.
(4) Draw 3rd set of n random two-digit number from table by the same steps independently of the 1st set & the 2nd set.
(5) Combine the respective random two-digit numbers of the three sets by the choice of the positions obtained in step (1) to obtain the n random six-digit numbers.
In order to draw n random six-digit numbers one can also proceed with the following steps:
(1) Draw three random two-digit numbers from the table independently of each other.
(2) Make a choice at random which set’s two-digit numbers will be placed at the left position, which set's two-digit numbers will be placed at the middle position and which set’s two-digit numbers will be placed at the right position while combining them in the formation of random six-digit numbers. This can be done by a random trial that results in six possible outcomes.
(3) Combine the three two-digit numbers, obtained in step (1), as per the selected choice of the positions obtained in step (2), to obtain one random six-digit number.
(4) Repeat the above three steps more (n-1) times to obtain n random six-digit numbers.
Example of drawing of random six-digit numbers:
Example -1: Let it be wanted to draw 20 random six-digit numbers from Table-1.
First way of drawing: Let a trial namely the throwing of an unbiased dice be performed to make a choice which set's twodigit number will be placed at the left position, which set’s twodigit number will be placed at the middle position and which set's two-digit number will be placed at the right position while combining them in the formation of random six-digit number. Suppose, the selected choice is as follows:
Two-digit number belonging to the 1st Set will be placed at the Left position, Two-digit number belonging to the 2nd Set will be placed at the Middle position& Two-digit number belonging to the 3rd Set will be placed at the Right position. Now let us draw the 1st set of 20 random two-digit numbers from Table-1. Let the numbers drawn be
47, 87, 59, 03, 37, 00, 50, 27, 52, 60, 51, 94, 70, 74, 26, 37, 46, 59, 78, 74.
Next, let us draw the 2nd set of 20 random two-digit numbers from the same table independently of the 1st set. Let the numbers drawn, in this case, be 90, 26,19, 94, 22, 02, 88, 46, 42, 29, 98, 02, 89, 26, 50, 18, 36, 11, 53, 54. Next, let us draw the 3rd set of 20 random two-digit numbers from the same table independently of the 1st set & of the 2nd set. Let the numbers drawn, in this case, be 40, 57, 52, 83, 36, 37, 39, 23, 10, 03, 33, 98, 96, 26, 32, 33, 72, 12, 32, 22. Now, let us combine the corresponding numbers drawn from the three tables as per the selected choice of combination. Thus, the selected 20 random six-digit numbers are 479040, 872657, 591952, 039483, 372236, 000237, 508839, 274623, 524210, 602903, 519833, 940298, 708996, 742626, 265032, 371833, 463672, 591112, 785332, 745422.
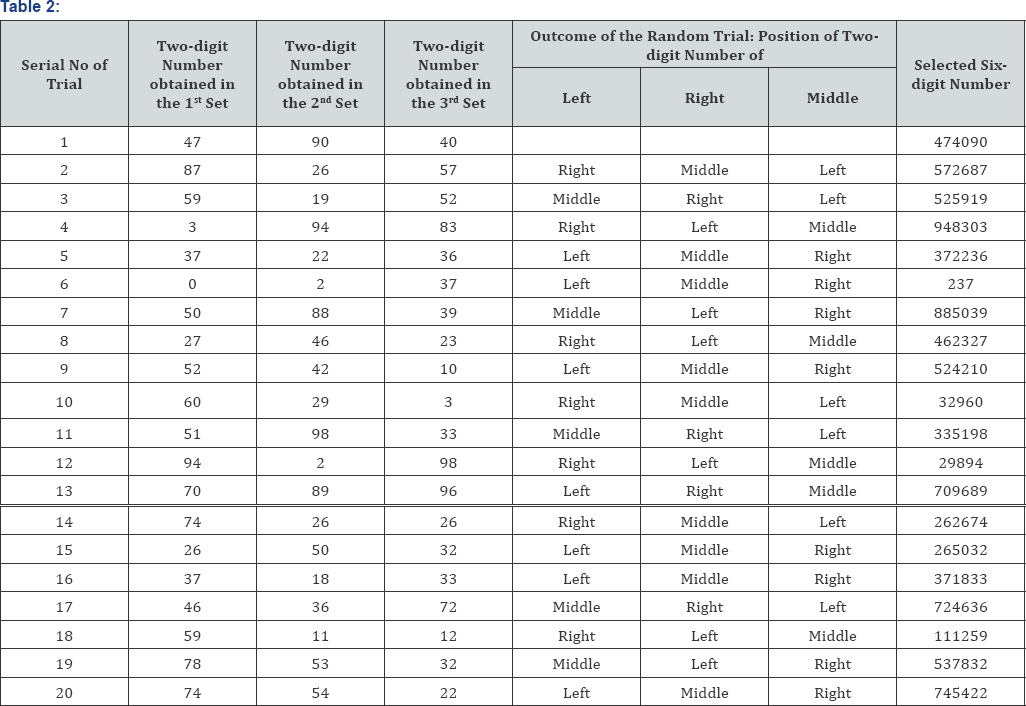
Second way of drawing: First, let us draw 3 random twodigit numbers independently to include in the three sets namely the 1st Set, the 2nd Set & the 3rd Set respectively from Table-1. Let the three numbers drawn be 47, 90, 40.Next, let a trial namely the throwing of an unbiased dice be performed to choice which table's two-digit numbers will be placed at the left position, which table’s two-digit numbers will be placed at the middle position and which table's two-digit numbers will be placed at the right position while combining them in the formation of random six-digit numbers. Suppose, the selected choice is as follows:
Two-digit number belonging to the 1st Set will be placed at the Left position, Two-digit number belonging to the 2nd Set will be placed at the Right position& Two-digit number belonging to the 3rd Set will be placed at the Middle position. Thus, the 1st selected six-digit random number is 474090. In order to obtain the remaining 19 random six-digit numbers, the two steps are to be repeated 19 times.
Let the outcomes of all the 20 trials be as follows:
Thus, the selected 20 random six-digit numbers to are 474090, 572687, 525919, 948303, 372236, 000237, 885039, 462327, 524210, 032960, 35198, 029894, 709689, 262674, 265032, 371833, 724636, 111259, 537832, 745422.
Drawing of random seven-digit numbers: Let d1d2 & d3d4 be two two-digit numbers drawn from Table-1 independently and d5d6d7 be one three-digit number drawn from Table-2. By similar logic as in the case of drawing of random four-digit numbers, it is obtained that each of the six seven-digit numbers d 1 d 2 d 3 d 4 d 5 d 6 d 7 , d 1 d 2 d 5 d 6 d 7 d 3 d 4 , d 3 d 4 d 1 d 2 d 5 d 6 d 7 , d 3 d 4 d 5 d 6 d 7 d 1 d 2 , d5d6d7d1d2d3d4, d5d6d7d3d4d1d2 is random. If a seven-digit number is selected from these six seven-digit numbers by performing a random trial consisting of six possible outcomes (for example by throwing of a fair dice), the selected number will be a random seven-digit number (Table 2).
If the process is repeated once, one more random seven-digit number can be obtained. By further repetitions, one can obtain more random seven-digit numbers. Thus, in order to draw n random seven-digit numbers one can proceed with the following steps:
(1) Make a choice, from among the three sets of which one is of random three-digit numbers & the other two are of random two-digit numbers, at random which set's numbers drawn will be placed at the left position, which set’s at the middle position and which set's at the right position while combining them in the formation of random seven-digit numbers. This can be done by a random trial that results in six possible outcomes.
(2) Draw the 1st set of n random two-digit number from Table-1.
(3) Draw the 2nd set of n random two-digit number from Table-1 independently of the 1st set.
(4) Draw a set of n random three-digit number from Table-2.
(5) Combine the respective numbers of the three sets by the choice of the positions obtained in step (1) to obtain the n random seven-digit numbers.
In order to draw n random seven-digit numbers one can also proceed with the following steps:
(1) Draw two random two-digit numbers independently from Table-1.
(4) Draw one random three-digit number from Table-2.
(5) Make a choice at random which of the three numbers drawn will be placed at the left position, which at the middle position and which at the right position while combining them in the formation of random seven-digit numbers. This can be done by a random trial that results in six possible outcomes as mentioned above.
(6) Combine the three drawn numbers as per the selected choice of the positions to obtain one random seven-digit number.
(4) Repeat the above steps more (n -1) times to obtain n random seven-digit numbers.
Example of Drawing of random seven-digit numbers
Example 1: Let it be wanted to draw 10 random seven-digit numbers. Let us make a choice, from among the three sets of which one is of random three-digit numbers & the other two are of random two-digit numbers, at random which set's numbers drawn will be placed at the left position, which set’s at the middle position and which set's at the right position while combining them in the formation of random seven-digit numbers.. Let the selected choice be that the numbers drawn from the 1st set of two-digit numbers & will be placed at left position & numbers drawn from the 2nd set of two-digit numbers at middle position respectively
Now, let us draw 10 random two-digit numbers from Table-A. Let the numbers drawn be 76, 58, 94, 39, 02, 60, 29, 33, 36, 08. Again, let us draw 10 random two-digit numbers from Table-1 independently of the 1st set. Let the numbers drawn be. Let the numbers drawn be 37, 90, 08, 58, 39, 15, 55, 38, 52, 77.
Next, let us draw 10 random three-digit numbers from Table-2. Let the numbers drawn be 811, 682, 707, 218, 966, 171, 020, 582, 591, 122 Thus the 10 random seven-digit numbers to be selected will be 7637811, 5890682, 9408707, 3958218, 0239966, 6015171, 2955020, 3338582, 3652591, 0877122.
Drawing of random eight-digit numbers: In order to draw random eight-digit numbers, there are two alternatives which will be called here as (i) Three-Three-Two Method and (ii) Two- Two-Two-Two Method.
A. Three-three-two method: Let 1d2d3, d4d5d 6, be two three-digit numbers drawn from the table of random three-digit numbers independently and d_7 d_8 be one two-digit number drawn from the table of random two-digit numbers. By similar logic as in the case of drawing of random four-digit numbers, it is obtained that each of the six eight-digit numbers d1d2d3 d4d5d6d7d8,d1d2d3d5d7 d8d4d5d6,d4d5d6d4d1d2 d3d5 d7d8,d4d5d6d7 d8d1d2d3,d7d8d1d2d3d4 d5d6,d7d8d4d5d6d1d2d2 is random. If one is selected from these six eight-digit numbers by performing a random trial consisting of six possible outcomes (for example by throwing of a fair dice) then the selected number will be a random eight-digit number. If the process is repeated once, one more random eightdigit number can be obtained.
By further repetitions, one can obtain more random eightdigit numbers. Thus, in order to draw n random eight-digit numbers one can proceed with the following steps:
(1) Make a choice at random which of the three numbers drawn will be placed at the left position, which at the middle position and which at the right position while combining them in the formation of random seven-digit numbers. This can be done by a random trial that results in 6 possible outcomes.
(3) Draw the 1st set of n random three-digit number from Table-2.
(3) Draw the 2nd set of n random three-digit number from Table-2 independently of the 1st set.
(4) Draw a set of n random two-digit number from Table-1.
(5) Combine the respective numbers of the three sets by the choice of the positions obtained in step (1) to obtain the n random eight-digit numbers.
In order to draw n random eight-digit numbers one can also proceed with the following steps:
(1) Draw two random three-digit numbers independently from Table-2.
(4) Draw one random two-digit number from Table-1.
(5) Make a choice at random which of the three numbers drawn will be placed at the left position, which at the middle position and which at the right position while combining them in the formation of random eight-digit numbers. This can be done by a random trial that results in six possible outcomes as mentioned above.
(6) Combine the three drawn numbers as per the selected choice of the positions to obtain one random eight-digit number.
(4) Repeat the above steps more (n -1) times to obtain n random eight-digit numbers.
B. Two-Two-Two-Two Choice: Let d_1 d_2, d_3 d_4, d_5 d_6, d_7 d_8 be four two-digit numbers drawn from the table of random two-digit numbers independently of each other. By similar logic as in the case of drawing of random four-digit numbers, it is obtained that each of the 24 eight-digit numbers
d1d2d3d4d5d6d7d8, d1d2d5d6d3d4d7d8,d3d4d1d2d5d6d7d8,d3d4d5 d6d1d2d7d8,d5d6d1d2d3d4d7d8,d5d6d3d4d1d2d7d8,
d1d2d3d4d7d8d5d6, d1d2d5d4d6d7d8d3,d4,d3d4d1d2d7d8d5d6,d3 d4d5d6d7d8d1d1,d5d6d1d2d7d8d3d4.d5d6d3d4d7d8d5d6
d1d2d7d8d3d4 d5d6,d1d2d7d8d5d6d7d8,d3d4,d3d4d7d8 d1d2d5d6,d3d4d7d4d8d5d6d1d2,d5d6d7d8d1d2d3d4, d5d6d7d8d3d4d1d2
d7d8d1d2d3d4d5d6,d7d8d1d2d5d6d3d4,d7d8d3d4d1d2d5d6, d7d8d3d4d5d6d1d2,d7d8d5d6d3d4d1d2 is random.
If one of them is selected by performing a random trial consisting of 24 possible outcomes then the selected number will be a random eight-digit number. If the process is repeated once, one more random eight-digit number can be obtained. By further repetitions, one can obtain more random eight-digit numbers. Therefore in order to draw n random eight-digit numbers from the table of random two-digit numbers, it is required to draw four independent sets, each of n random two-digit numbers, from the table [41]. It is to be noted that any successive two digits of different eight-digit numbers can be same. Conversely, with the same successive two digits there can be different eightdigit numbers. Therefore, the random two-digit numbers in each of the four independent sets of random two-digit numbers, drawn in order to form random eight-digit numbers, need not necessarily be distinct.
Thus, in order to draw n random eight-digit numbers from the table of random two-digit numbers one can proceed with the following steps:
(1) Make a choice at random which set's two-digit numbers will be placed at the left position, which set’s two-digit numbers will be placed at the 1st middle position from the left, which set's two-digit numbers will be placed at the 2nd middle position from the left and which set's two-digit numbers will be placed at the right position while combining them in the formation of random eight-digit numbers. This can be done by a random trial that results in 24 possible outcomes.
(2) Draw 1st set of n random two-digit number from Table-A.
(3) Draw 2nd set of n random two-digit number from Table- 1independently of the 1st set.
(4) Draw 3rd set of n random two-digit number from Table- 1independently of the 1st set & the 2nd set.
(5) Draw 4th set of n random two-digit number from Table- 1independently of the earlier sets.
(6) Combine the respective random two-digit numbers of the four sets by the choice of the positions obtained in step (1) to obtain the n random eight-digit numbers.
In order to draw n random eight-digit numbers one can also proceed with the following steps:
(1) Draw four random two-digit numbers from Table- 1independently of each other.
(2) Make a choice at random which of the four two-digit numbers will be placed at the left position, which at the 1st middle position from the left, which at the 2nd middle position from the left and which the right position while combining them in the formation of random eight-digit numbers. This can be done by a random trial that results in 24 possible outcomes.
(3) Combine the four two-digit numbers, obtained in step(1) , as per the selected choice of the positions obtained in step (2), to obtain one random eight-digit number.
(4) Repeat the above three steps more (n - 1) times to obtain n random eight-digit numbers.
Example of drawing of random eight-digit numbers
Example 1: Let it be wanted to draw 10 random eight-digit numbers.
First Way of Drawing : Let us make a choice, by performing a trial, numbers belonging to which set will be placed at the left position, which set at the middle position and which set at the right position while combining them in the formation of random eight-digit numbers. Let the selected choice be that the two-digit numbers drawn from Table-1will be placed at left position, the three-digit numbers in the 1st set at middle position & the threedigit numbers in the 2nd set at right position.
Now, let us draw 10 random two-digit numbers from Table-A. Let the numbers drawn be 30, 80, 35, 60, 29, 15, 83, 06, 81, 47. Now, let us draw the 1st set of 10 random three-digit numbers from Table-2. Let the numbers drawn be 520, 185, 881, 527, 310, 101, 873, 647, 990, 724
Next let us draw the 2nd set of 10 random three-digit numbers from Table-2 independently of the 1st set of random three-digit numbers. Let the numbers drawn be 092, 393, 709, 460, 106,318, 504, 138, 529, 481
Thus the 10 random eight-digit numbers to be selected will be 09230520, 39380185, 70935881, 46060527, 10629310, 31815101, 50483873, 13806647, 52981990, 48147724.
II. Second way of drawing: Let us make a choice, by performing a trial, numbers belonging to which set will be placed at the left position, which set at the 1st middle position from the left, which set at the 2nd middle position from the left & which set at the right position while combining them in the formation of random eight-digit numbers. Let the selected choice be that the two-digit numbers belonging to the 1st set will be placed at left position, belonging to the 2nd set at the 1st middle position from the left, belonging to the 3rd set at the 2nd middle position from the left & belonging to the 4th set at the right position [42]. Now, let us draw the 1st set of 10 random two-digit numbers from Table-A. Let the numbers drawn be
30, 80, 35, 60, 29, 15, 83, 06, 81, 47.
Next, let us draw the 2nd set of 10 random two-digit numbers from Table-1 independently of the 1st set. Let the numbers drawn be 50, 18, 88, 52, 31, 01, 73, 47, 99, 24
Next, let us draw the 3rd set of 10 random two-digit numbers from Table-1 independently of the 1st & the 2nd sets. Let the numbers drawn be 92, 39, 09, 46, 61, 38, 50, 18, 29, 41
Again, let us draw the 4th set of 10 random two-digit numbers from Table-1 independently of the 1st, the 2nd & the 3rd sets. Let the numbers drawn be 44, 87, 00, 38, 60, 48, 22, 06, 44, 99. Thus the 10 random eight-digit numbers to be selected will be 30509244, 80183987, 35880900, 60524638, 29316160, 15013848, 83735022, 06471806,81992944,47244199.
Drawing of random nine-digit numbers
Let d1d2d3,d4d5d6,d7d8d9 be 3 three-digit numbers, drawn independently of each other, from the table of random three-digit numbers. By similar logic as in the case of drawing of random four-digit numbers, it is obtained that each of the 6 nine-digit numbers d1d2d3d4d5d6d7d8d9, d1d2d3d7d8d9d4d5d6, d4d5d6d1d2d3d7 d8d9,d4d5 d 6 d 7 d 8 d 9 d 1 d 2 d 3 ,Sd 7 d 8 d 9 d 1 d 2 d 3 d 4 d 5 d 6 , d 7 d 8 d 9 d 4 d 5 d 6 d 1 d 2 d 3 , is random.
If one is selected from these 6 nine-digit numbers by performing a random trial consisting of 6 possible outcomes then the selected number will be a random nine-digit number.
If the process is repeated once, one more random nine-digit number can be obtained. By further repetitions, one can obtain more random nine-digit numbers. Therefore in order to draw n random nine-digit numbers from the table of random three-digit numbers, it is required to draw three independent sets, each of n random three-digit numbers, from the table. It is to be noted that any successive three digits of different nine-digit numbers can be same. Conversely, with the same successive three digits there can be different nine-digit numbers. Therefore, the random three-digit numbers in each of the three independent sets of random three-digit numbers, drawn in order to form random nine-digit numbers, need not necessarily be distinct [43,44].
Thus, in order to draw n random nine-digit numbers one can proceed with the following steps:
(1) Make a choice at random which set's will be placed at the left position, which set’s two-digit numbers will be placed at the middle position and which set's two-digit numbers will be placed at the right position while combining them in the formation of random six-digit numbers. This can be done by a random trial that results in 6 possible outcomes namely.
(2) Draw 1 st set of n random three-digit number from Table-2.
(3) Draw 2 nd set of n random three-digit number from Table-2 independently of the 1st set.
(4) Draw 3rd set of n random three-digit number from Table-2 independently of the 1st set & the 2nd set.
(5) Combine the respective random three-digit numbers of the three sets by the choice of the positions obtained in step (1) to obtain the n random nine-digit numbers.
In order to draw n random nine-digit numbers one can also proceed with the following steps:
(1) Draw 3 random three-digit numbers from the table independently of each other.
(2) Make a choice at random which three-digit numbers will be placed at the left position, which at the middle position and which at the right position while combining them in the formation of random nine-digit numbers. This can be done by a random trial that results in 6 possible outcomes.
(3) Combine the 3 three-digit numbers, obtained in step (1), as per the selected choice of the positions obtained in step(2) , to obtain one random nine-digit number.
(4) Repeat the above three steps more (n - 1) times to obtain n random nine-digit numbers.
Example of Drawing of random nine-digit numbers:Example -1: Let it be wanted to draw 10 random nine-digit numbers. Let us make a choice, by performing a trial, three-digit numbers of which set will be placed at the left position, which at the middle position and which at the right position while combining them in the formation of random nine-digit numbers. Let the selected choice be that the numbers in the 1 st set will be placed at left position, numbers in the 2 nd set at middle position & numbers in the 3 rd set at right position respectively [45]. Now, let us draw the 1 st set of 10 random three-digit numbers from Table-2. Let the numbers drawn be
292, 408, 577, 216, 066, 228, 701, 028, 753, 577.
Next, let us draw the 2nd set of 10 random three-digit numbers from Table-2. Let the numbers drawn be
063, 528, 502, 460, 106, 318, 504, 138, 529, 530.
Again, let us draw the 3rd set of 10 random three-digit numbers from Table-2. Let the numbers drawn be
874, 993, 018, 898, 799, 476, 202, 467, 180, 557.
Thus the 10 random nine-digit numbers to be selected will be
292063874, 408528993, 577502018, 216460898, 066106799, 228318476, 701504202, 028138467, 753529180, 577530180.
Conclusion
In this paper, methods of drawing of random m-digit numbers have been discussed for m = 2, 3, 4, 5, 6, 7, 8, 9. Methods of drawing of random m-digit numbers for m > 9 can be derived in a similar manner. The significance of this paper is that the methods developed here enables us to draw random m-digit numbers (for 2 < m < 9) with the help of either a single table of random two-digit numbers or a single table of random threedigit numbers or both of the two tables as the case may be.
References
- Tippett LHC (1927) Random Sampling Numbers. Tracts for Computers no. 15, Cambridge University Press, Cambridge, England.
- Mahalanobis PC (1934) Tables of random samples from a normal population. Sankya 1:289-328.
- Kendall MG, Smith BB (1938) Randomness and Random Sampling Numbers. Jour Roy Stat Soc 101(1): 147-166.
- Fisher R A, Yates F (1938) Statistical Tables for Biological, Agricultural and Medical Research (Edn. 6 th ), Longman Group Limited, England 134-139.
- Hald A (1952) Table of random numbers. In: A. Hald. Statistical Tables and Formulas, Wiley.
- Royo J, Ferrer S (1954) Tables of Random Numbers Obtained from Numbers in the Spanish National Lottery. Trabajos de Estadistica 5: 247-256.
- Rand Corporation (1955) A Million Random Digits. Free Press, Glenoe, Ireland.
- Quenouille MH (1959) Tables of Random Observations from Standard Distributions. Biometrika 46(1): 178-202.
- Moses EL, Oakford VR (1963) Tables of Random Permutations George Allen & Unwin.
- Rao CR, Mitra SK, Matthai A (1966) Random Numbers and Permutations. Statistical Publishing Society, Calcutta.
- Snedecor GW, Cochran WG (1967) Statistical Methods. Iowa State University Press, Ames, Iowa.
- Rohlf FJ, Sokal RR (1969) Ten Thousand Random Digits. In: Rohlf, Sokal, Statistical Tables, Freeman.
- Manfred Mohr (1971) Le Petit Livre de Nombres au Hasar. Édition d'artiste, Paris.
- Chakrabarty D (2010) Chakrabarty's Definition of Probability: Proper Randomness of Fisher and Yates Random Number Table. Int J Agricult Stat Sci 6(2): 461-469.
- Sarmah BK, Chakrabarty D (2014a) Examination of Proper Randomness of the Number Generated by LHC Tippett. International Journal of Engineering Sciences & Research Technology 3(12): 631-638.
- Sarmah BK, Chakrabarty D (2014b) Testing of Randomness of the Number Generated by Fisher and Yates ”, International Journal of Engineering Sciences & Research Technology 3(11): 632-636.
- Sarmah BK, Chakrabarty D (2014c) Examination of Proper Randomness of the Number Generated by LHC Tippett. International Journal of Engineering Sciences & Research Technology, 3(12): 631-638.
- Sarmah BK, Chakrabarty D (2015a) Testing of Proper Randomness of the Table of Number Generated by MG Kendall and B Babington Smith (1939). International Journal of Engineering Sciences & Research Technology 4(2): 260-282.
- Sarmah BK, Chakrabarty D (2015b) Testing of Randomness of the Numbers Generated by Fisher and Yates. AryaBhatta J Math & Info 7(1): 87-90.
- Sarmah BK, Chakrabarty D (2015c) Examination of Proper Randomness of the Numbers Generated by LHC Tippett (1927). IOSR Journal of Mathematics 11(3): 35-37.
- Sarmah BK, Chakrabarty D (2015d) Examination of Proper Randomness of the Numbers Generated by Rand Corporation: t-Test. International Journal of Innovative Research in Science, Engineering and Technology 4(10): 9536-9540.
- Sarmah BK, Chakrabarty D (2015e) Testing of Proper Randomness of the Numbers Generated by Kendall and Babington Smith: t-Test. AryaBhatta J Math Info 7(2): 365-368.
- Sarmah BK, Chakrabarty D (2015f) Examination of Proper Randomness of Numbers of M. G. Kendall and B. Babington Smith's Random Numbers Table: Run Test. International Journal of Multidisciplinary Research and Modern Education I(II): 223- 225.
- Sarmah BK, Chakrabarty D (2015) Testing of Randomness of the Numbers Generated by Fisher and Yates: Run Test. International Journal of Innovative Research in Science, Engineering and Technology 4(12): 11956-11958.
- Chakrabarty D (2013a) One Table of Random two-digit Numbers. AryaBhatta J Math Info 5(1): 141-152.
- Chakrabarty D (2013b) One Table of Random three-digit Numbers. AryaBhatta J Math Info 5(2): 285 -294.
- Chakrabarty D (2016a) One More Table of Random Two-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 3(3): 1667-1678.
- Chakrabarty D (2016b) One More Table of Random Three-Digit Numbers”, International Journal of Advanced Research in Science, Engineering and Technology 3(4): 1851-1869.
- Chakrabarty D (2016c) Drawing of Random Six-Digit Numbers from Tables of Random Three-Digit Numbers”, International Journal of Advanced Research in Science, Engineering and Technology 3(8): 25072515.
- Chakrabarty D (2016d)Drawing of Random Six-Digit Numbers from Tables of Random Two-Digit Numbers”, International Journal of Advanced Research in Science, Engineering and Technology 3(9): 26432655.
- Chakrabarty D (2016e) Drawing of Random Four-Digit Numbers from Independent Tables of Random Two-Digit Numbers in Selection of Random Sample. Biometrics & Biostatistics International Journal 4(7): 00118.
- Chakrabarty D (2016f) Drawing of Random Five-Digit Numbers from Tables of Random Two-Digit and Three-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 3(7): 2385-2306.
- Chakrabarty D (2016i) Drawing of Random Six-Digit Numbers from a Single Table of Random Two-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 3(10): 2743-2753.
- Chakrabarty D (2016j) Drawing of Random Six-Digit Numbers from a Single Table of Random Three-Digit Numbers”, International Journal of Advanced Research in Science, Engineering and Technology 3(11), 2905 - 2914.
- Chakrabarty D (2016k) Drawing of Random Seven-Digit Numbers from Tables of Random Two-Digit Numbers and of Three-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 3(12): 3003-3012.
- Chakrabarty D (2016l) Drawing of Random Four-Digit Numbers from Independent Tables of Random Two-Digit Numbers in Selection of Random Sample. Biometrics & Biostatistics International Journal 4(7): 00118.
- Chakrabarty D (2017a) Drawing of Random Four-Digit Numbers from a Single Table of Random Two-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 4(2): 3377-3387.
- Chakrabarty D (2017b) Drawing of Random Nine-Digit Numbers from a Single Table of Random Two-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 4(3): 3566-3575.
- Chakrabarty D (2004) A Theoretical Definition of Probability Based on Common Sense, Bulletin of Pure and Applied Sciences 23(2): 343-349.
- Chakrabarty Dhritikesh (2011) Probability in Ideal Situation and in Practical Situation. Arya Bhatta J Math & Info 3 (1): 161-168.
- Chakrabarty D (2016g) Drawing of Random Six-Digit Numbers from Tables of Random Three-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 3(8): 2507-2515.
- Chakrabarty D (2016h) Drawing of Random Six-Digit Numbers from Tables of Random Two-Digit Numbers. International Journal of Advanced Research in Science, Engineering and Technology 3(9): 26432655.
- Sarmah BK, Chakrabarty D, Barman N (2015) Testing of Proper Randomness of the Table of Number Generated by Rand Corporation (1955). International Journal of Engineering Sciences & Management 5(1): 97-119.
- Kendall MG, Smith BB (1939) A Table of Random Sampling Numbers. Tracts for Computers no. 24, Cambridge University Press, Cambridge, England.
- Sarmah BK, Chakrabarty D, Barman N (2015) Testing of Proper Randomness of the Table of Number Generated by Rand Corporation (1955). International Journal of Engineering Sciences & Management 5(1): 97-119.






























