Discrimination between Earthquakes and Explosion Using MLP and RBF Neural Networks
Mostafa AllamehZadeh1 and Jamal Mahmoudi2
1Assistant professor, International Institute of Earthquake Engineering and Seismology (IIEES), Iran
2PhD student,International Institute of Earthquake Engineering and Seismology (IIEES), Iran
Submission: April 10, 2017; Published: August 17, 2017
*Corresponding author: Mostafa Allameh Zadeh, Assistant professor, International Institute of Earthquake Engineering and Seismology (IIEES), Email: zadeh66@hotmail.com
How to cite this article: Mostafa A Z Jamal M. Discrimination between Earthquakes and Explosion Using MLP and RBF Neural Networks. Biostat Biometrics Open Acc J. 2017: 2(4): 555595. DOI: 10.19080/BBOAJ.2017.02.555595.
Abstract
The discrimination of small earthquakes from explosions based on the seismic signal recorded at teleseismic distances is an important and difficult task. The characteristics of a seismic signal are related to the energy release of the event through a complex functional relationship. The elastic and an elastic response characteristics of the propagation paths, and the response characteristics of seismometers, are undesired effects that usually fade the inherent source properties of seismometers. This shows that preprocessing stage, that performs a transformation from data space into a feature space to remove redundancy from recorded signals, is a critical process. In this study, 26 earthquakes from Eurasian events, and 25 underground nuclear explosions, which have occurred in East Kazakhstan (Semipalatinsk) test site is selected.
Vertical components of the short period teleseismic records of these events is used. In order to reduce the mentioned disturbing effects, the following preprocessing are performed: In the first step, instrumentation correction was performed on all of the input records. In the second step, in order to extract suitable features from the P-wave, each record was filtered through 0.5 to 4Hz, using a fourth - order band pass Butterworth filter, and in the last step, as spectral characteristics suffer from the attenuation effects of the propagation paths, the spectra of p-wave were corrected for the effect of seismic attenuation. Constant level fl, spectral corner frequency fc, and high-frequency spectral slop s, are features extracted from corrected P-wave spectrum, in this research. Another feature, obtained from spectrum, which is used is P-coda/P spectral ratio from 1 to 5 Hz.
Recent developments of the neural network classifiers indicate that they are useful for solving many difficult real-world problems in discriminate analysis and pattern classification with powerful theoretical supports. According to successful and satisfactory history of neural networks, and by using the mentioned preprocessing methods, the current study is going to used two powerful type of neural networks, multilayer perceptron and radial basis function, in order to develop a discrimination model to separate the earthquakes from the explosions.
As a results, 4 different models is conducted in this study. Two types of neural networks, MLP and RBF, and for each network two different datasets is used, P-coda/P spectral ratio and the values of fl- fc- s. According to the results, it can be concluded that the preprocessed method which applied to the data were very suitable, and by use of neural networks and these preprocessed data, discrimination of the earthquakes and the explosions can be done with high reliability and precision.
Keywords:Discrimination; Earthquake; Explosion; Preprocessing of data; MLP; RBF; Neural network
Abbreviations: ANN: Artificial Neural Networks; MLP: Multilayer Perceptron Neural Networks; RBF: Radial Basis Function Neural Network
Introduction
The discrimination of small earthquakes from explosions based on the seismic signal recorded at teleseismic distances is an important and difficult task. The characteristics of the seismic signals recorded at teleseismic observation points following an event, are related to the energy released by the event through a complex functional relationship. This function involves among many variables such as the source, medium, depth, as well as the inelastic and an elastic response characteristics of the propagation paths traversed by the waves from the source to receivers, and also the response characteristics of the seismometers used to record the motion. In Pattern Recognition applications for discrimination and classification problems in seismology many algorithms and models have been proposed for many tasks, especially for clustering, regression and classification. The problem of distinguishing underground nuclear explosions from earthquakes using seismic data has been studied for a long time. Many researchers have reported discrimination results for regional data [1-6]. In most of these studies, spectral characteristics of the records have been used as potential features for discrimination.
However, classification of small magnitude events using spectral data is still a difficult task, especially for short-period body-waves, recorded at long distances. Conventional methods for discrimination between earthquakes and explosions at regional distances have concentrated on extracting specific features such as amplitude ratios, measures of waveform complexity or various kinds of spectral ratios. This criterion and other routine seismic discriminate cannot succeed because there are many causes for changing (time-varying) spectra of the complexity of body-wave. The broad reason for changing spectra is the propagation of waves through a medium is quite complicated but the basic effect is that waves of different frequencies propagate with different velocities. The other important effect in propagation is the attenuation and absorption of a wave. The amount of attenuation depends on the medium and the frequency [7-9].
In the context of seismic source identification, it is customary to use traditional classifiers, like linear or quadratic classifiers [10]. These conventional statistical classifiers are in capable of forming arbitrary decision surfaces. These classifiers are optimum only under the assumption of Gaussian distribution of data. They cannot form complex, highly nonlinear, and disconnected regions in the feature space of classes with significant overlaps. On the other hand, recent developments of the neural network classifiers indicate that they are useful for solving many difficult real-world problems in discriminate analysis and pattern classification [11], with powerful theoretical supports [12]. There are three major advantages of neural networks. First, neural networks are able to learn any complex non-linear mapping. Second, they do not make a priori assumption about the distribution of data. Third, they are very flexible with respect to incomplete, missing and noise data and therefore eliminate concern about this issue [13].
Neural networks have been used successfully to solve complicated pattern recognition and classification problems in different domains such as optimization and nonlinear programming [14], construction engineering [15], video and audio analysis [16], and financial forecasting [17]. Also, related to the applying Artificial Neural Networks (ANN) in the problems of predicting the earthquake, there are some conducted researches with successful results [18-21]. A classic example of discriminate analysis occurs in parametric statistics, in which the quadratic Fisher discriminate is used to separate two classes defined on the same feature space which are assumed to obey Gaussian distributions [22-24].
According to successful and satisfactory history of neural networks, and by considering valuable experiences of previous researches in preprocessing of data for discrimination of earthquakes and explosions, the current studyis going to used pre-processed data in two powerful type of neural networks, multilayer perceptron and radial basis function, in order to develop a discrimination model to separate the earthquakes from the explosions.
Multilayer perceptron and radial basis function neural networks
Multilayer perceptron neural networks (MLP): All The model neurons, connected up in a simple fashion, were given the name "perceptron" by Frank Rosenblatt in 1962. In a large number of complicated math problems, where their solution depends on solving tough non-linear equations, MLP neural networks are very helpful, and can easily be employed by defining proper weights and functions. MLP neural networks consist of several layers of nodes. It includes an input layer, an output layer, and a hidden layer, each of which contains input node(s) which are called sensory, output node(s) which are called responding nodes, and hidden node(s), respectively (Figure 1).
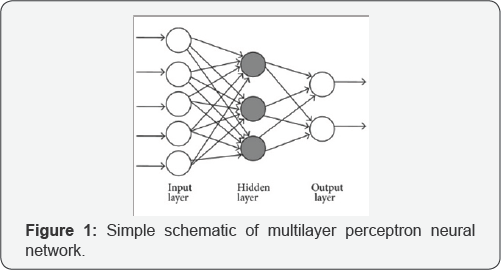
The MLP neural network which is used in this research consists of an input layer, one hidden layers and an output layer. The hidden layer contains unobservable network node(s). For the hidden layer 20 hidden nodes is chosen. Each hidden node is a function of the weighted sum of the inputs. The function is the activation function, and the values of the weights are determined by the Levenberg-Marquardt algorithm. The sigmoid activation function is used for the hidden layer and linear activation function is used for the output layer. The input nodes are based on input variables, which will be discussed in the next section, and there is an output node which is based on our target, an earthquake or an explosion.
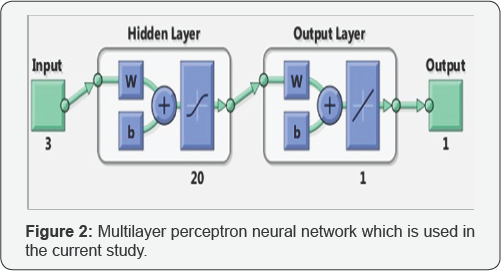
A well-known concern with neural networks is “overtraining”. To ease this problem, the network, at most, can have 10 validation fail. It means that if the network in 10 epochs in a row doesn't have any progress in decreasing the errors, the training process will stop. A schematic of multilayer perceptron network which is used in the current study is depicted in Figure 2.
Radial basis function neural network (RBF): The design of a supervised neural network may be pursued in a variety of ways. In RBF neural networks there is a completely different approach by viewing the design of a neural network as a curve fitting (approximation) problem in high-dimensional space. According to this view point, learning is equivalent to finding a surface in a multi-dimensional space that provides a best fit to the training data, with the criterion for "best fit” being measured in some statistical sense. Correspondingly, generalization is equivalent to the use of this multi-dimensional surface to interpolate the test data. Such a view point is the motivation behind the method of radial-basis functions in the sense that it draws upon research work on traditional strict interpolation in a multi-dimensional space [25].
In the context of a neural network, the hidden nodes provide a set of "functions" that constitute an arbitrary "basis" for the input patterns (vectors) when they are expanded into the hidden space; these functions are called radial basis functions. Radial basis functions were first introduced in the solution of the real multivariate interpolation problem. The early work on this subject is surveyed by Powell in1987 [26]. Broomhead & Lowe in 1988 [27] were the first to exploit the use of radial basis functions in the design of neural networks. Another major contribution to the theory and design of radial basis function networks is due to Poggio & Girosi [28]. It is now one of the main fields of research in numerical analysis.
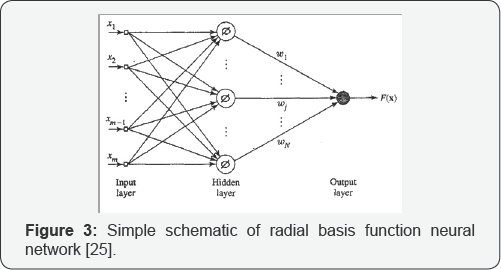
The construction of a radial basis function (RBF) network, in its most basic form, involves three layers with entirely different roles. The input layer is made up of source nodes (sensory units) that connect the network to its environment. The second layer, the only hidden layer in the network, applies a nonlinear transformation from the input space to the hidden space; in most applications the hidden space is of high dimensionality. The output layer is linear, supplying the response of the network to the activation pattern (signal) applied to the input layer, Figure 3.
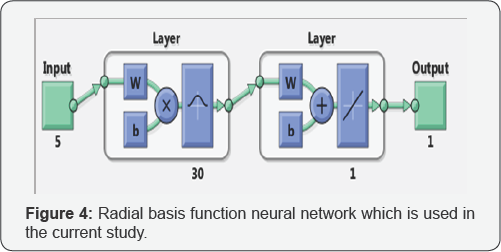
RBF neural networks which is used is a two-layer network. The first layer has radial basis neurons, and the second layer has pure linear neurons. Both layers have biases. In training process, neurons adds to the hidden layer(radial basis layer) of network, up to a specified maximum number of neurons, until it meets the specified mean squared error goal. Initially the radial basis layer has no neurons. The following steps are repeated until the network's mean squared error falls below goal or its number of radial basis neurons exceeds the maximum number of neurons. In RBF neural networks which is used in this research, maximum number of neurons is 30, mean squared error goal is equal to zero and spread of radial basis functions is equal to 1. A schematic of RBF neural network which is used in the current study is depicted in Figure 4.
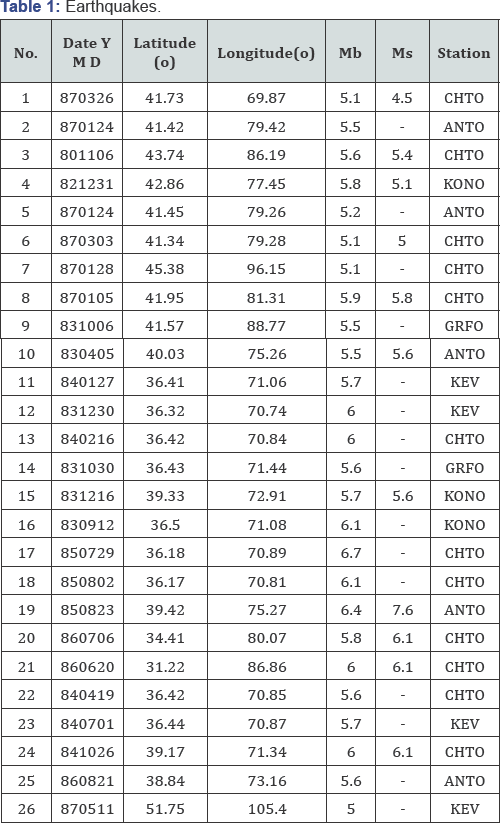
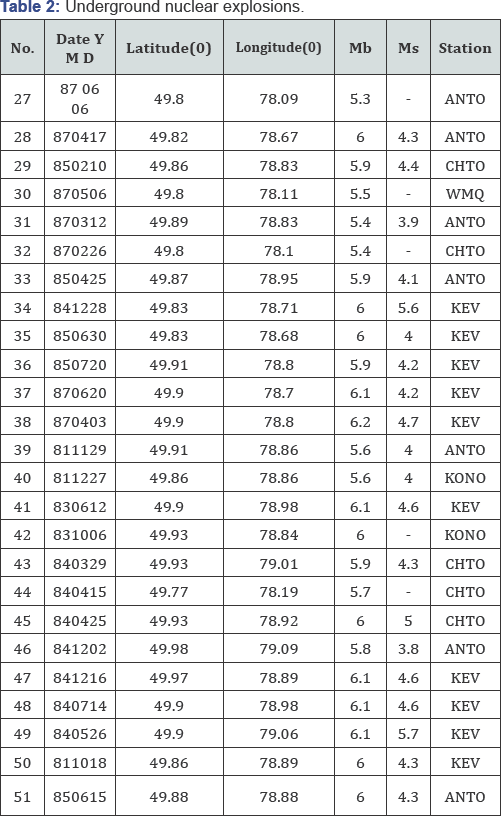
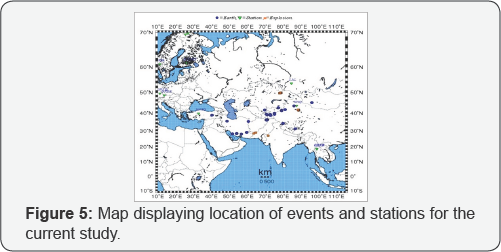
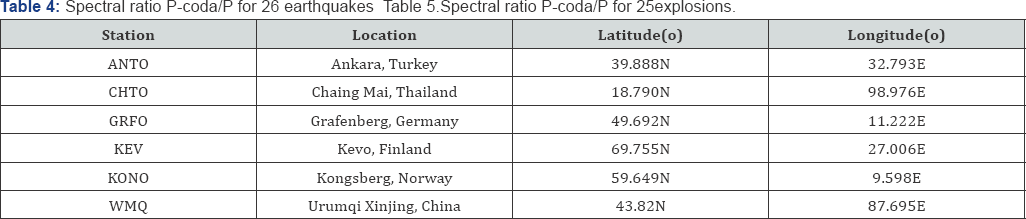
Event selections: In this study, 26 earthquakes from Eurasian events, Table 1, and 25 underground nuclear explosions, which have occurred in East Kazakhstan (Semipalatinsk) test site, Table 2, is selected. Vertical components of the short period teleseismic records is used. These signals have been extracted from a 10 volumes set of CD-ROM’s, provided by the USGS/NEIC. Table 3 shows names and locations of the selected stations and two typical examples of our seismograms, an earthquake signal and an underground nuclear explosion signal, are shown in Figure 5.
Preprocessing of Data and Feature Extraction: The preprocessing stage is a critical process that performs a transformation from data space into a feature space to remove redundancy from recorded signals. The characteristics of a seismic signal, especially those recorded at far distances, are related to the energy release of the event through a complex functional relationship. The elastic and an elastic response characteristics of the propagation paths, and the response characteristics of seismometers, are undesired effects that usually fade the inherent source properties of seismometers. In order to reduce these disturbing effects, the following preprocessing are performed:
• In the first step, instrumentation correction was performed on all of the input records, based on the given instrument frequency response or pole zero diagram on the CD-ROM’s.
• In the second step, in order to extract suitable features from the P-wave, each record was filtered through 0.5 to 4Hz, using a fourth- order band pass Butterworth filter. As a consequence of this operation, the surface- reflected pP phase appeared more clearly; and so, appropriate lengths of windows lengths depend on the magnitude, the epicenter distance, and the bandwidth of filter.
Finally, although spectral characteristics of the p-wave can usually provide reasonable classification results, they suffer from the attenuation effects of the propagation paths. These effects are more severe for the spectra of short- period records [7]. So, in the last step, the spectra of p-wave were corrected for the effect of seismic attenuation. Seismic attenuation was approximated by the usual exponential attenuation law [4], with a frequency independent Q. Although many similar studies [7,29] indicate that a frequency- dependent Q model is, in general, necessary. However, it is found 'The spectral shape in the 0.5-4 Hz band can also be fitted by a frequency- independent Q model' [30]. It should be mentioned that distance correction is a by-product of the attenuation correction; since epicenter distance is a parameter of the exponential attenuation law.
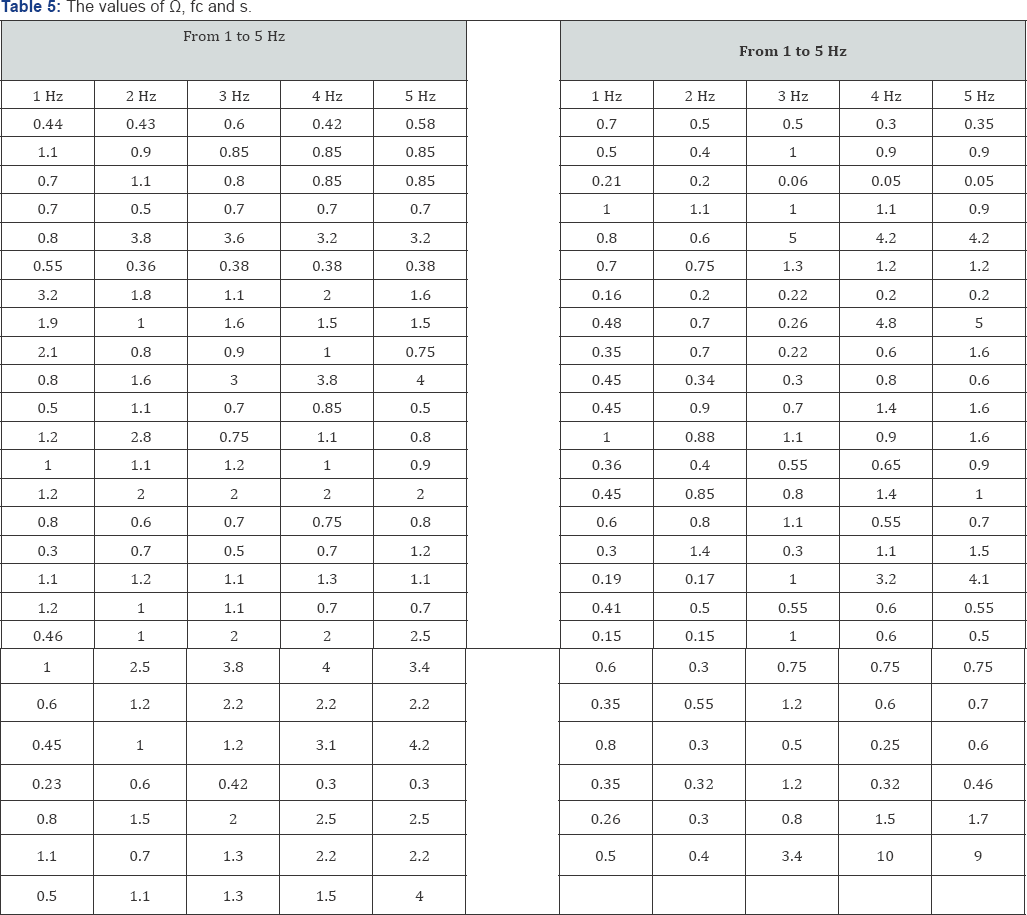
A wide variety of seismic signals are classified on the basis of spectral signatures. Recent detector algorithms based on the pattern recognition and artificial neural networks use the moving window spectrum and spectrograms in solving problems in signal discrimination. A spectrogram is a two-dimensional image that includes both temporal and frequency information. In this study, two straight lines, in a double logarithmic scale, approximate each corrected P-wave spectrum. These two lines are uniquely determined by three parameters: constant level Ω, spectral corner frequency fc, and high-frequency spectral slop s. For each event, these source parameters are obtained via a least squares fitting procedure. Another features, obtained from spectrum, which is used in this research is P-coda/P spectral ratio from 1 to 5 Hz.
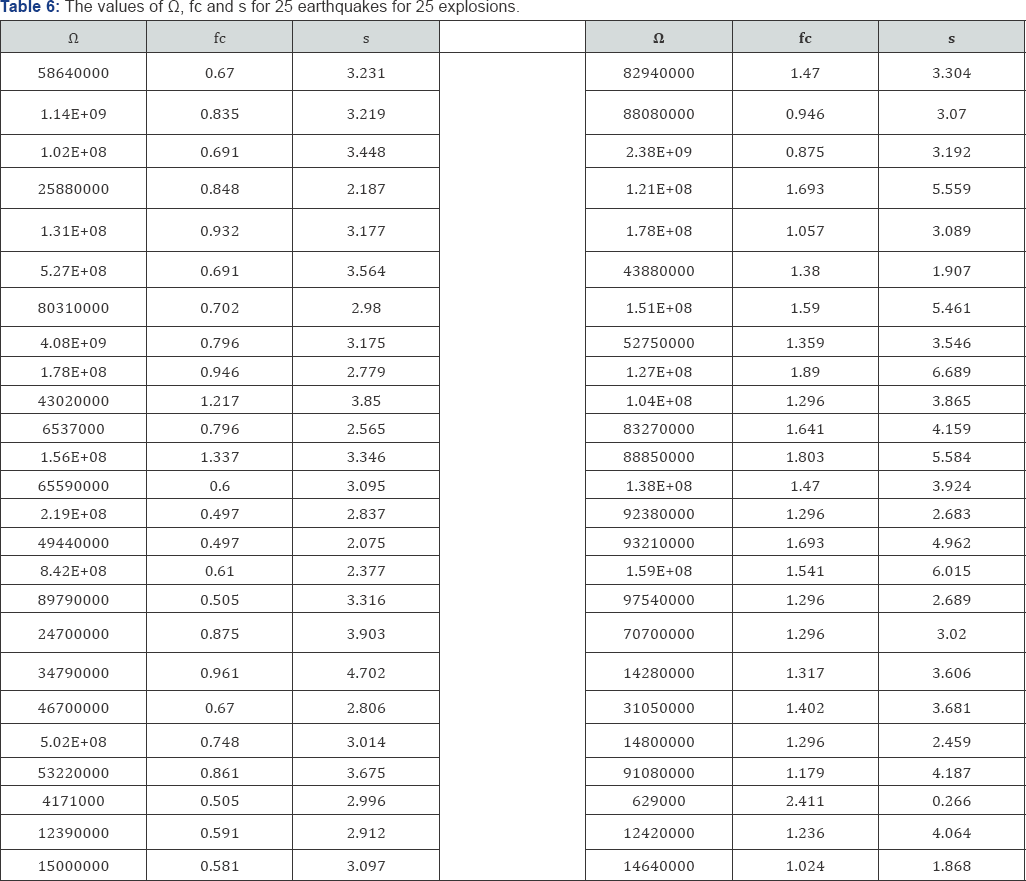
As a results, there are two different datasets which will be used as the neural networks inputs. First dataset including 5 inputs: P-coda/P spectral ratio from 1 to 5 Hz, Table 4 & 5, and second dataset including three inputs: constant level Ω, spectral corner frequency fc, and high-frequency spectral slop s, Table 6 .
Results and Discussion
As, in this study, 2 types of neural networks, MLP and RBF, and for each network 2 different datasetsis used, P-coda/P and Ω-fc- s, 4 different models is conducted. It should be noted that in all models, for output of datasets, in order to quantization of outputs, number 1 is used instead of earthquakes and number -1 is used instead of explosions. Results of each models is as following subsections
MLP network with P-coda/P dataset
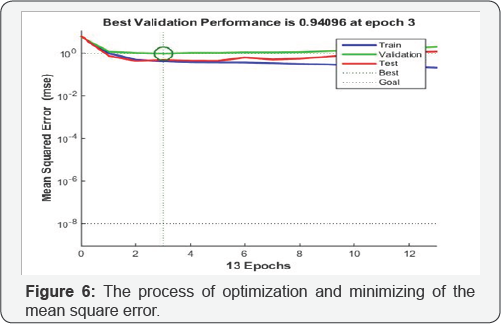
Results of MLP network with P-coda/P dataset is depicted in Figures 6 & 7. Figure 6 shows the process of optimization and minimizing of the mean square error. As can be seen in this graph, the error reaches to its minimum in the third epoch and after that overtraining is happened and in the following 10 epochs, no progress is seen. So the training process is stopped. Figure 7 contains 4 graphs, each of which shows the performance of the network in training, validation and testing processes, and totally, respectively. As can be seen, the network after training and validation process, has a very good performance in testing process with regression equal to 0.88 (R=0.88) and at all with R=0.71.
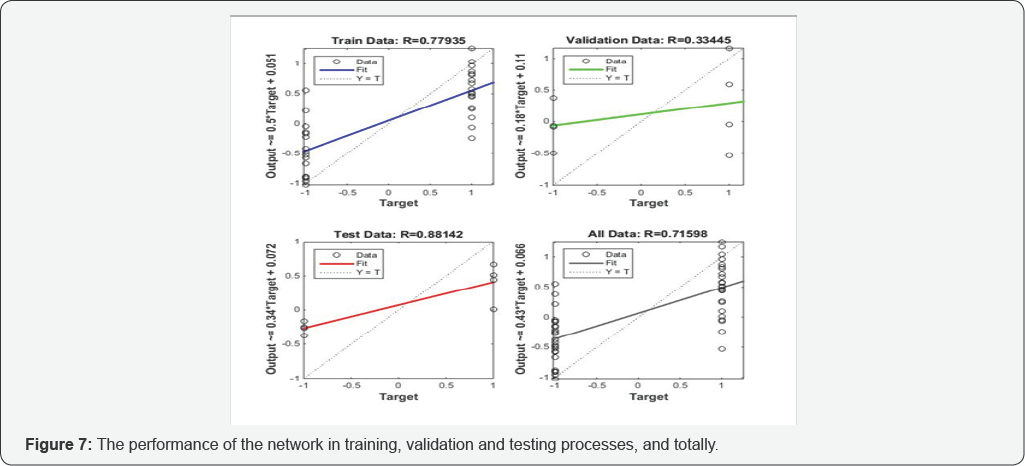
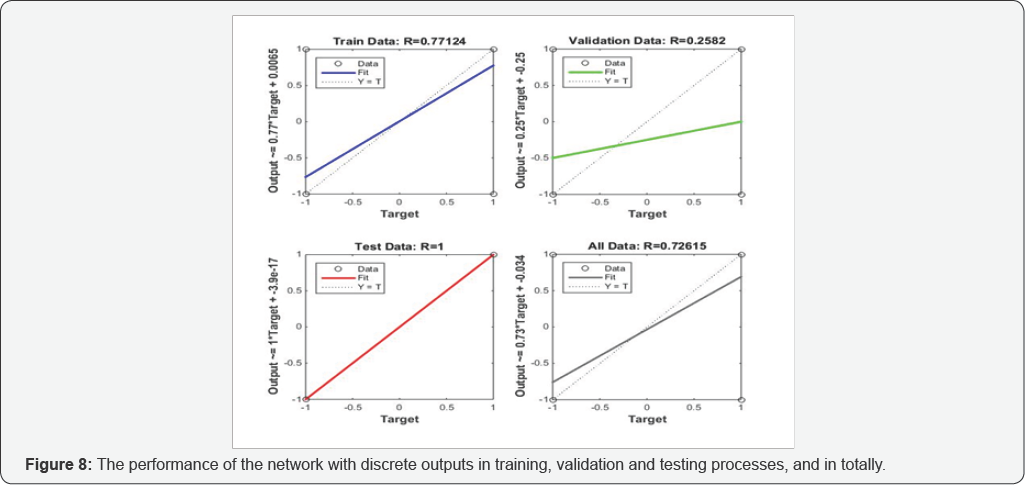
Although the targets of network are just 1 and -1 and are in discrete space, as is clear in Figure 7, the outputs of network are in continuous space. For solving this problem, positive outputs rounded to 1 and negative outputs rounded to -1. The results of this solution is depicted in Figure 8. As can be seen in this graph, the results of the network is improved and the network in testing process successfully discriminated the earthquakes and the explosions in all cases with R=1. This shows high ability of this model in generalizing.
RBF neural network with P-coda/P input.
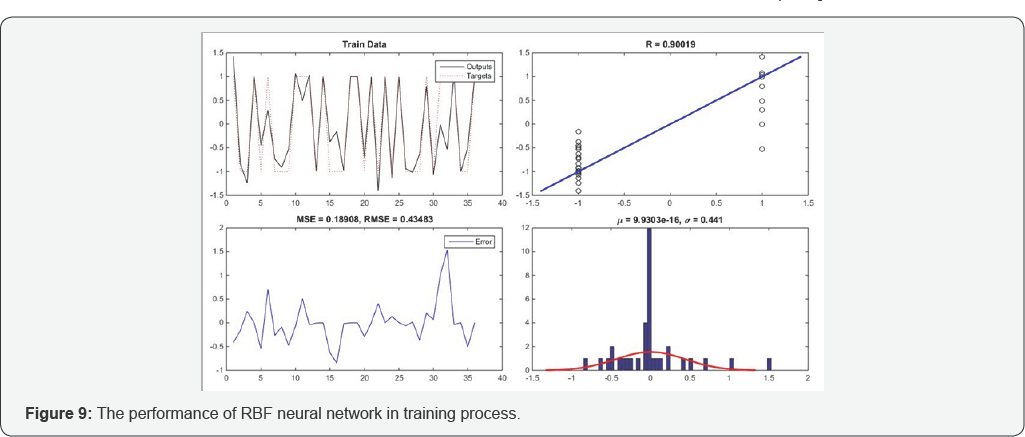
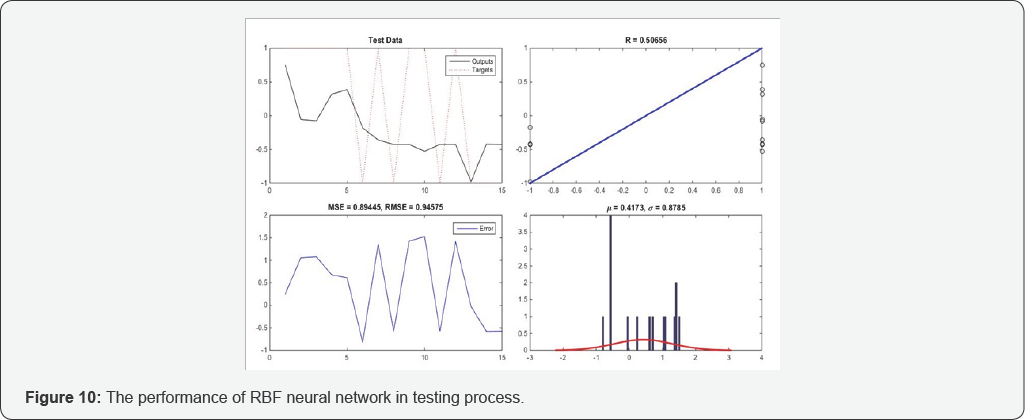
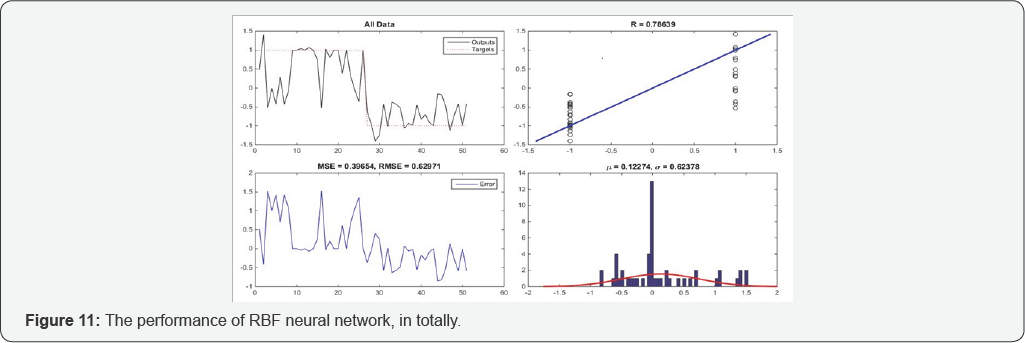
Results of RBF neural network with P-coda/P dataset is depicted in Figures 9-11. Figure 9 shows 4 graphs and these graphs are: targets and outputs of network graph, regression graph, errors graph containing the mse and the rmse values, and errors histogram, all for training process and data. Figures 10 and 11 are same as Figures 9, but for testing process and in totally, respectively. According to results of training process, based on Figure 9, the RBF network learning ability is very good and it can approximate training data with high precision but in generalizing, based on Figure 10, it's weaker than previous model.
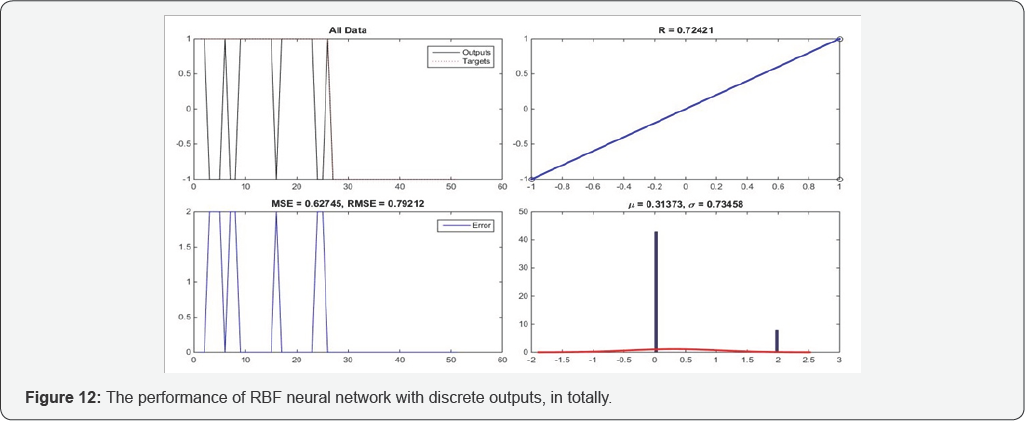
In totally, based on data obtaining from Figure 11 such as the regression value or the mse value, this model has done a good performance. It will be clearer after doing rounding process in following. Same as previous model, this model has the problem of continuous outputs. So, rounding process in the way that said in the previous subsection, have done. The results of network after this process is depicted in Figure 12. This figure shows targets and outputs of network graph, regression graph, errors graph, and errors histogram for all data. As can be seen in this figure, in errors histogram, the network has more than 40 correct discrimination (more than 80%) and this shows the good performance of the model.
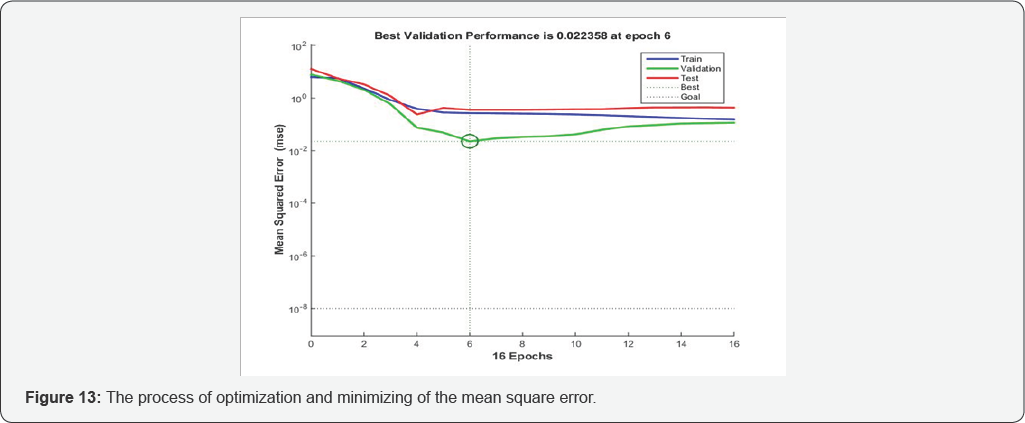
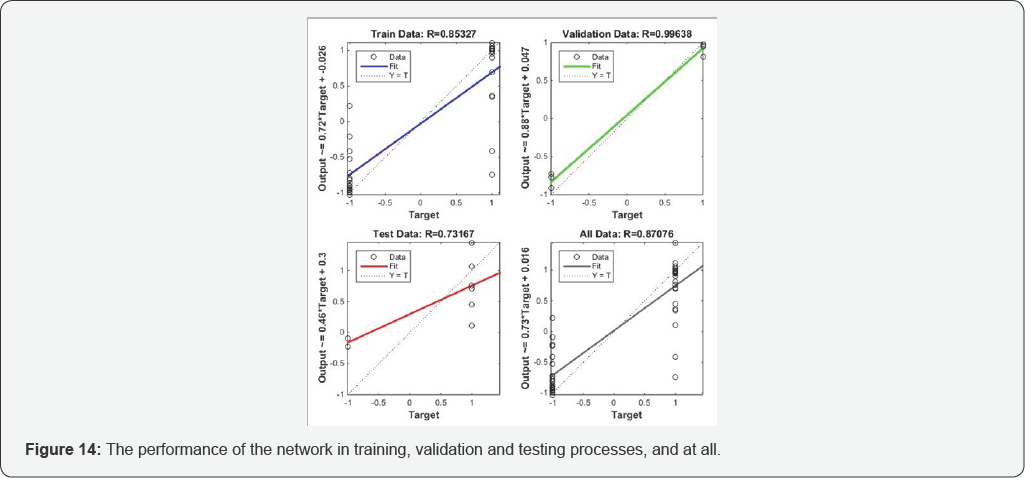
MLP neural network with constant level (Ü), spectral corner frequency (fc), and high-frequency spectral slop (s) inputs. Results of MLP network with Ü, fc, and s values dataset is depicted in Figures 13 & 14. In Figure 13 which shows the process of minimizing of the mean square error, it can be seen that the value of mean square error reaches to its minimum in the 6th epoch. Figure 14 in 4 graphs shows the performance of the network in training, validation and testing processes, and totally, respectively. As can be seen in this figure, the network has a very good performance in all training, validation and testing processes with high regression value in all levels and in total.
As said before, for solving the problem of continuous outputs of network, positive outputs rounded to 1 and negative outputs rounded to -1. The results of this solution is depicted in Figure 15. As can be seen in this graph, the performance of the network is excellent and the network in both validation and testing processes has the highest possible performance (%100 correct discrimination). This shows that this model (MLP neural network with Ω, fc, and s values dataset) has high ability in both learning and generalizing and it can discriminate the earthquakes and the explosions with high precision. The results of this model is the best between all models.
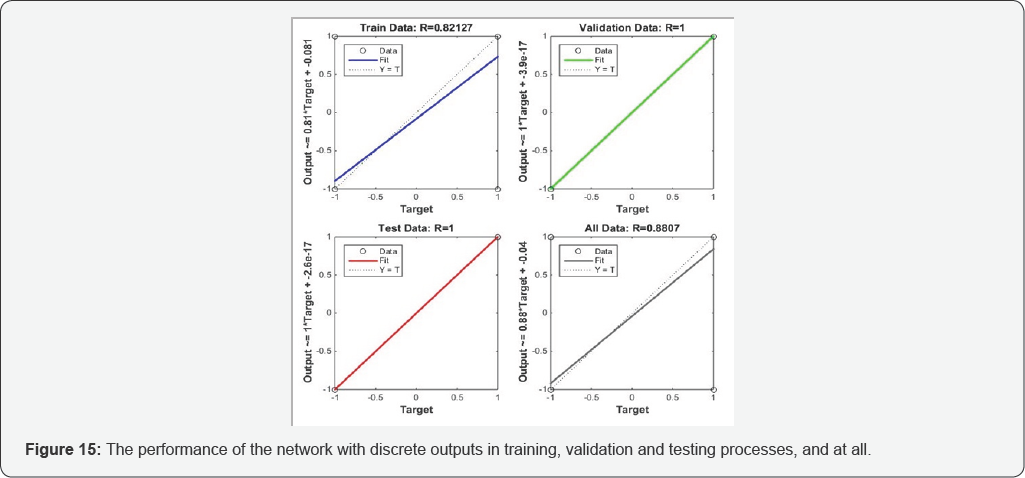
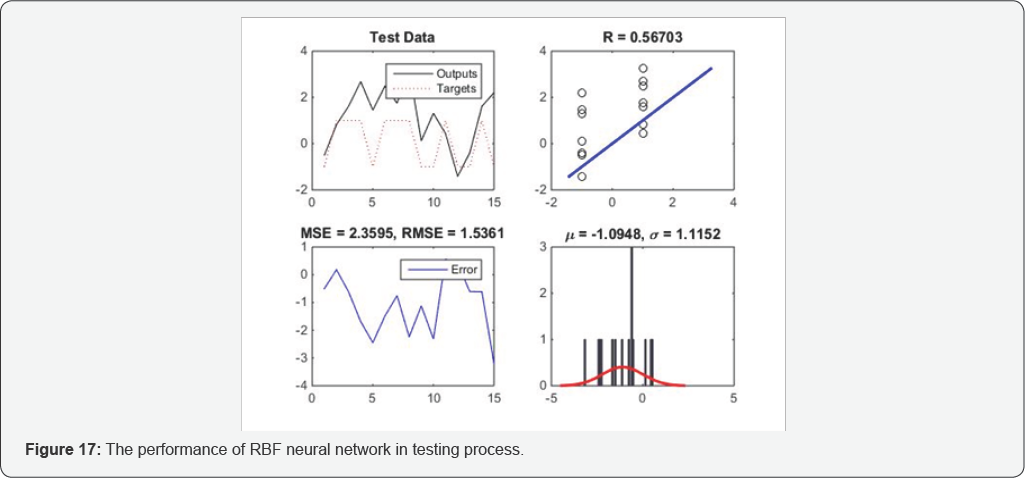
RBF neural network with constant level (Ω), spectral corner frequency (fc), and high-frequency spectral slop (s)inputs. Results of RBF neural network with Ω, fc, and s values dataset is depicted in Figures 16-18 for training process, testing process, and in totally, respectively. Each of these 3 figures shows 4 graphs and these graphs are: targets and outputs of network graph, regression graph, errors graph containing the MSE and the RMSE values, and errors histogram. According to Figure 16, results of training process, again it can be seen the RBF network learning ability is very good but in generalizing, based on Figure 17, it's weaker than MLP models.
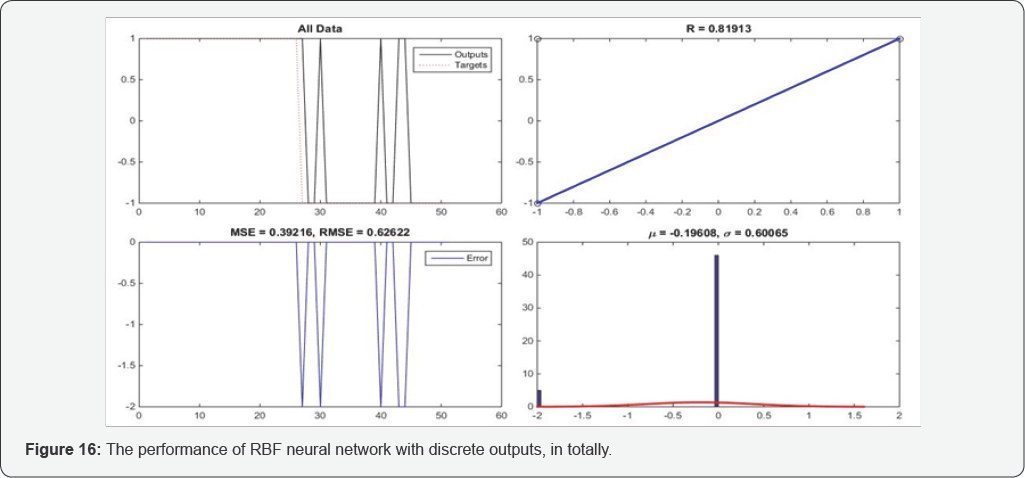
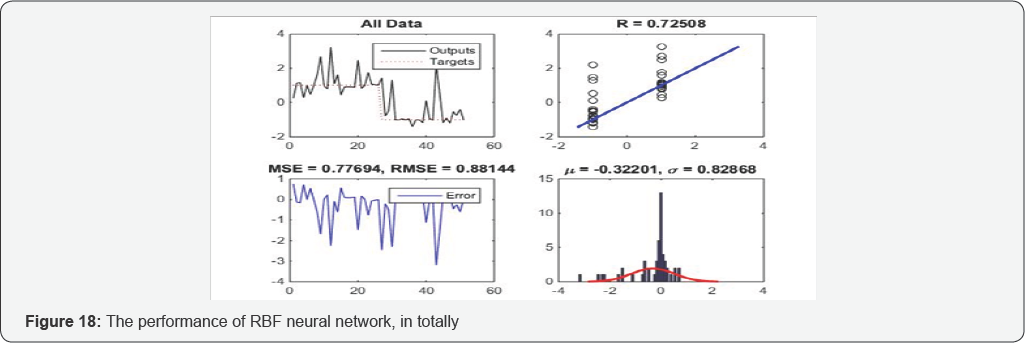
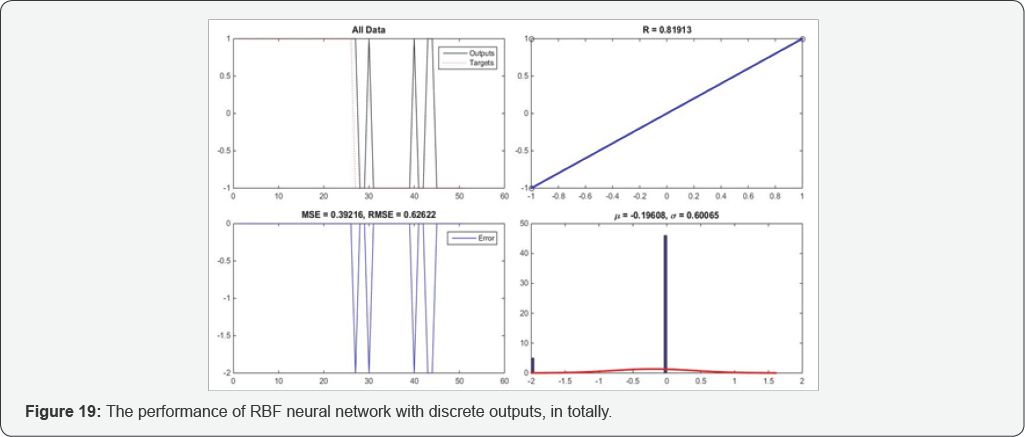
Based on data obtaining from Figure 18, in totally, this model also has done a good performance and it can be seen that its performance is better than the RBF model with P-coda/P dataset. Same as all previous models, rounding process have done for this model, too. The results of network after this process is depicted in Figure 19. This figure shows targets and outputs of network graph, regression graph, errors graph, and errors histogram for all data. As can be seen in this figure, in errors histogram, the network has done45 correct discriminations (90%) and this shows very good performance of the model. It also shows better performance of this model than the other RBF model with P-coda/P dataset.
Conclusion
In this research, discrimination of the earthquakes and the explosions by use of preprocessed data and neural networks were studied. After doing three precious preprocessing level, two different dataset, P-coda/P spectral ratio and the values of fl, fc, and s, extracted from data. Also, two powerful kind of neural networks, MLP and RBF, were selected to be used in study. As a results four different models were studied. The results show that all models have good performances and high ability in discrimination of the earthquakes and the explosions. From the results, it can be concluded that the preprocessed method which applied to the data were very suitable and by use of both datasets, the purpose of discrimination is met with high accuracy. However, the results show that dataset of the values of fl, fc, and sis a better than the dataset of P-coda/P spectral ratio for this discrimination.
The results also clarified that the MLP neural network is more suitable and more match with discrimination problem of this research than the RBF neural network. RBF Neural network, in this case of study, although was very good in learning and training process, was a little weak in generalization. But the MLP neural network had a good performance in both learning and generalization. The model with MLP neural network and using the values of fl, fc, and s was the best model between all models. This model in validation and testing phases have done 100% correct discrimination.
At last, according to the results, it can be concluded that the preprocessed method which applied to the data were very suitable, and by use of the neural networks and these preprocessed data, discrimination of the earthquakes and the explosions can be done with high reliability and precision.
References
- Pomeroy PW, Best WJ, Mc Evilly TV (1982) Test ban treaty verification with regional data- a review. Bull Seism Soc Am 72: 89-129.
- Taylor SR, Denny MD, Vergino ES, Glaser RE (1989)Regional Discrimination between NTS Explosions and western US Earthquakes. Bull Seism Soc Am 79: 1142-1176.
- Pulli JJ, Dysart PS (1990) An Experiment in the Use of Trained Neural Networks for Regional seismic Event Classifications. Geophys Res Lett 17(7): 977-980.
- Dowla FU, Taylor SR, Anderson R (1990) seismic Discrimination with Artificial Neural Networks: preliminary Results with Regional spectral Data. Bull Seism Soc Am 80: 1910-1933.
- AllamehZadeh M, Hadizadeh M (1998) Discrimination between Earthquake and Nuclear explosion using SOM. Pajouheshnameh 6: 4.
- AllamehZadeh M (2011) Discrimination analysis of Earthquakes and Man-made Events Using ARMA Coefficients Determination by Artificial Neural Networks. Natural Resources Research Journal 20(4): 367-375.
- Cormier VF (1982) The Effect of Attenuation on seismic Body waves. Bull Seism Soc Am72: S169-S200.
- Murphy JR, Barker BW, O’Donnell A (1989) Network- Averaged Teleseismic p- wave spectra for Underground Explosions, part I. Definitions and Examples. Bull Seism Soc Am 89: 141-155.?
- Murphy JR (1989) Network- Averaged Teleseismic p- wave spectra for underground Explosions, part II. Source characteristics of pahute mesa Explosions. Bull Seism Soc Am 79: 141-155.
- Kim WY, Simpson DW, Richard PG (1993) Discrimination of Earthquakes and Explosions in the Eastern United States Using Regional High-Frequency Data. Geophys Res Lett 20(14): 1507-1510.
- Lippman RP (1989) Pattern classification using neural networks. IEEE Communication Mag 27(11): 47-64.
- Farago A, Lugosi G (1993) strong Universal Consistency of Neural Network classifiers. IEEE trans. Theory 39(4): 1146-1151.
- Vellido A, Lisboa PJG, Vaughan J (1999) Neural Networks in Business: A Survey of Applications (1992-1998). Expert Systems with Applications 17: 51-70.
- Chen YY, Young KY (2007) An SOM-based algorithm for optimization with dynamic eight updating. Int J Neural Syst 17(3): 171-181.
- Senouci AB, Adeli H (2001) Resource scheduling using neural dynamics model of Adeli and Park. Journal of Construction Engineering and Management, ASCE 127(1): 8-34.
- Fyfe C, Barbakh W, Ooi W C, Ko H (2008) Topological mappings of video and audio data. Int J Neural Syst 18(6): 481-489.
- Chih Fong T, Yen Jiun Ch (2009) Earnings Management Prediction: A Pilot Study of Combining Neural Networks and Decision Trees. Journal of Expert Systems with Applications 36: 7183-7191.
- Moustra Maria, Marios Avraamides, Chris Christodoulou(2011) Artificial neural networks for earthquake prediction using time series magnitude data or Seismic Electric Signals. Expert Systems with Applications 12(38): 15032-15039.
- Alexandridis A, Chondrodima E, Efthimiou E, Papadakis G, Vallianatos F, et al.(2014) Large Earthquake Occurrence Estimation Based on Radial Basis Function Neural Networks. IEEE Transactions on Geoscien 52(9): 5443-5453.
- Mahmoudi J, Rezaei M, Mohammadi MH (2015) Prediction of the Earthquake Moment Magnitude by Use of the Multilayer Perceptron Neural Network. 7th International Conference on Seismology & Earthquake Engineering.
- Mahmoudi J, Arjomand MA, Rezaei M, Mohammadi MH (2016) Predicting the Earthquake Magnitude Using the Multilayer Perceptron Neural Network with Two Hidden Layers. Civil Engineering Journal 2(1): 1-12.
- Alexander (1992) Identification of Earthquakes and Explosions Using pattern Recognition Techniques on Frequency- Slowness seismic Images. EOS 73: 360.
- Allamehzadeh M, Nassery P (1997) Seismic Discrimination Using a Fuzzy Discriminator. Pajouheshnameh, IIEES, Tehran. Iran.
- Allamehzadeh M (1999) Seismic Source Identification Using SelfOrganizing Technique. 3th International Conference on Seismology & Earthquake Engineering.
- Haykin S (1999) Neural networks; a comprehensive foundation. second edition.
- Powell MJD (1987) Radial basis functions for multivariable interpolation: a review. In: Mason JC and Cox MG (Eds) Algorithm for Approximation. Clarendon Press, Oxford.
- Broomhead DS, David Lowe (1988) Multivariable Functional Interpolation and Adaptive Networks. Complex Systems Publications, Inc 2: 3.
- Poggio T, Girosi F (1990) Extension of a theory of networks for approximation and learning: dimensionally reduction and clustering. In: Proceeding Image Understanding Workshop 597-63. Pittsburgh, USA.
- Der ZA, Less AC (1985) Methodologies for Estimating t (f) from short- period Body Waves and Regional variations of t (f) in United states. Geophys J 82(1): 125-140.
- Burger RW, Lay T, Burdick LJ (1987) Average Q and yield Estimates from the pahute Mesa test site. Bull Seism Soc Am 77: 1274-1294.






























