Biostatistics and Biometrics Open Access Journal

Mini Review

Development of Predictive Signatures for Treatment Selection in Precision Medicine

Un Jung Lee¹, ShengLi Tzeng², Yu-Chuan Chen¹ and James J Chen^1,3*

¹Division of Bioinformatics and Biostatistics, National Center for Toxicological Research, USA

²Department of Public Health, China Medical University, Taiwan

³Department of Biostatistics, University of Arkansas for Medical Science, Arkansas

Submission: March 06, 2017; Published: August 17, 2017

*Corresponding author: James J Chen, National Center for Toxicological Research, US Food and Drug Administration, USA; Email: JJChen@uams.edu

How to cite this article: Un Jung Lee, ShengLi Tzeng, Yu-Chuan Chen, James J. Chen Development of Predictive Signatures for Treatment Selection in Precision Medicine. Biostat Biometrics Open Acc J. 2017: 2(4):555594. DOI: 10.19080/BBOAJ.2017.02.555594.

Abstract

Precision medicine applies molecular technologies and statistical methods to identify biomarkers that indicate differential disease out comes or treatment responses for better matching of disease with specific therapies to optimize treatment assignment. The success of precision medicine lies in the development of biomarker-based treatment selection strategy to identify right patients for the right treatment. Development of treatment selection strategy consists of three steps:

I. Biomarker identification,

II. Subgroup selection, and

III. Clinical utility assessment via subgroup analysis.

Biomarker identification involves fitting an interaction models to identify a set of potential predictive biomarkers from the measured genomic variables. Subgroup selection develops a prediction model based on the biomarkers identified to partition patients into subgroups that are homogeneous with respect to disease outcomes and/or responses to a specific treatment. Clinical utility assessment evaluates accuracy of patient treatment assignment and assesses enhancement of treatment efficacy. Procedures described are illustrated by simulations and analysis of breast cancer dataset.

Keywords: Biomarker identification; Interaction test; Subgroup selection; Tailored therapy

Introduction

Advances in molecular technology have shifted the development of new drugs towards precision medicine, identifying patient subgroups likely to benefit from a targeted treatment. Today, many cancer treatments are being developed for targeted therapies [1-8], in which only a subpopulation of patients is expected to benefit from the therapy. The term "personalized (precision) medicine", which is commonly referred to the right treatment for the right patient at the right time, has been used to convey the concept of customizing medical therapies to select best treatments tailored to the individual patients. In conventional drug development, it is based on the concept of "one-size-fits all", and assumed that the drug effect is similar for all patients with the particular disease. However, if a drug is only effective for a small proportion of patients, this drug may not be available for those needed patients since drug's approval is based on mean difference between treated and untreated patients based on the entire patient population.

The success of precision medicine lies in the patient treatment-selection strategy to identify patient subgroups for which a particular therapy is beneficial, and for the patients in complementary subgroup the therapy is unnecessary or possibly harmful. Subgroups refer to a subset of patients defined by baseline and/or disease characteristics with respect to a specific clinical endpoint. The baseline and disease characteristics include demographics, genetics variants, phenotypic variables, disease stages, and tumor subtypes [9,10]. These characteristics, referred as "biomarkers," provide indicators of status of an organism of a particular health condition, disease state and susceptibility, or response to a therapy.

Biomarkers for treatment-selection can generally be classified into two major types, prognostic and predictive biomarkers. Prognostic biomarkers are indicators of overall disease, regardless of treatment. The Onco type DX™ 21 gene signature [11] is the well-known breast cancer prognostic test that predicts patients with degree of risk for information to select the appropriate treatment. Predictive biomarkers are indicators of the likelihood of patient's response to a particular treatment. The known predictive biomarkers are: Herceptin treatment for HER2-postive [12] and tamoxifen treatment for ER/PR-positive breast cancers [12, 13], Erlotinib treatment for epidermal growth factor receptor mutation for non-small cell lung carcinomas [13]. Prognostic and predictive biomarkers have been discussed extensively [14]. Notice that prognostic biomarkers and predictive biomarkers are not mutually exclusive.

Development of biomarker-based strategies for treatment decisions can be divided into three components:

I. Biomarker identification,

II. Subgroup selection, and

III. Clinical utility assessment via subgroup analysis.

Biomarker identification involves fitting regression models to identify a set of potential prognostic and/or predictive biomarkers from measured genomic variables. Subgroup selection develops prediction (prognostic and predictive) models based on the biomarkers identified to partition patients into subgroups that are homogeneous with respect to disease outcomes or treatment effects. Prognostic models identify patients as good prognosis (low risk) versus poor prognosis (high risk). The predictive models identify patients who are suitable for the treatment (responders) and who are not suitable (non-responders). In the context of targeted therapy, this article focuses on predictive model to identify responder and nonresponder subgroups. Clinical utility assessment infers that the treatment-selection strategy can classify patients accurately and improve the power to detect treatment effect so that effective drugs are available for the needed the patients to receive the treatment.

Methods

Biomarker identification

Let m be the number of measurements (Z₁,..,Z_m) investigated and n be the total number of patients in the experiment. In clinical efficacy studies, the measurements are made and collected before the randomization. Thus, the treatment should not have effects on those measurements. For a given patient, let z^ij denote the j-th measurement (j = 1, ..., m) in the i-th patient(i = 1, ..., n), and y^it denote the clinical outcome of interest for the i-th patient in the t-th treatment. The notation y^it is simplified as yⁱ since the index are completely determined by i. The outcome variable can be binary, continuous, and time-to-event onset. When the number of variables is relatively large, the univariate variable-by-variable analysis is commonly used to identify the variables that are associated with the target variable. The conventional regression model for subgroup analysis [15,16] includes the genomic variable z_ij and treatment T as main effects and the variable-by-treatment interaction (T*z_ij ):

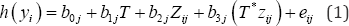
Equation (1) is a generalized linear regression model where h(y_i) is a log it function when y is binary, an identify function when y is continuous, and a Cox proportional hazard function in log form when y is a survival endpoint. This article focuses on binary outcomes.

This model is commonly used for subgroup analysis to identify a variable (factor) that shows differential subgroup effects [17-22]. The coefficient b_3j measures differential treatment effects in the sampled patients implicated by different value of z_ij . A significant b_3j implies a significant difference in treatment responses between underlying subgroups (responders and nonresponders) in the variable z_ij. Let T denote the set of significant variables z's at a predetermined level; T is the set of candidate predictive biomarkers.

Equation (1) has been known to be lack of power for assessing interaction effects b_3j's. Freidlin and Simon [16] presented an alternative model without the main effect term z_ij to identify candidate predictive biomarkers:

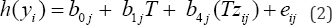
A significant interaction coefficient b_4j indicates a difference in the outcomes between subgroups due to difference either in underlying disease prognosis or in treatment response in the variable z_ij. The set of significant variables, denoted as U, would consist of both prognostic biomarkers (S) and predictive biomarkers (T).

Subgroup selection

Subgroup selection is to develop classification strategy to stratify patients into responder and non-responder subgroups based on the biomarkers identified. Classification algorithms depend on the type of target variables. For binary outcome variables, the observed outcomes (positive and negative) can be used as the class labels. The subgroup selection, then, can be regarded as a standard class prediction problem. The commonly used class prediction algorithms in genomic and personalized medicine applications include logistic regression, classification trees and random forests, linear and diagonal discriminant analysis, support vector machines, etc. [23-28]. In this article, we used diagonal linear discriminant analysis (DLDA) [26], since it has been shown to perform well and was robust against imbalanced subgroups sizes [29] even with considerable size difference, a common occurrence in subgroup selection.

Clinical utility assessment

Assessment of a biomarker-based predictive model mainly evaluates whether the predictive model fits for its intended context of use. It does not to determine whether individual biomarkers are predictive. It is to determine if the predictive model is useful for treatment selection including:

1. Accuracy of the subgroup selection and

2. Enhancement of treatment efficacy to detect treatment effect on the selected responder patients.

For binary responses, the common performance measures are sensitivity (the proportion of correct identification of responder patients out of total responders), specificity (the proportion of correct identification of non-responder patients out of total non-responders), and accuracy (the total number of correct identifications). For patient treatment assignment, it is desirable that the prediction model should have high sensitivity and high specificity, which implies high accuracy. In confirmatory clinical trials, enhancement of treatment efficacy via subgroup analyses of responders would involve testing two hypotheses. The first hypothesis is a comparison between the treatment and control arms for the whole trial population at α₁ significance level, the second hypothesis is a comparison on the responder subgroup at α₁ significance level, where at α₁ + α₂ = α, the overall family wise error rate.

Simulation study

Biomarker identification: The simulation design considered a two-arm experiment with a sample size of 600 patients, where 300 patients were randomly assigned to each arm. Two thousand covariates were generated from a normal distribution. Among them, there were 10 prognostic biomarkers, 10 predictive biomarkers, and 5 predictive and prognostic biomarkers. These 25 biomarkers were generated from N(1,0.2² ), the remaining 1975 covariates were generated from N(0,0.2²). One thousand pair of training and test sets was simulated; the training dataset was used to develop the procedure and the test dataset was used for evaluation.

In the simulation design, the proportion of responders π = 0.2. The expected numbers of responder and non-responder subgroups are 60 and240, respectively. The target variable was binary with "positive" or "negative" response. The probability of a positive outcome p for each subgroup was generated by the logit model:

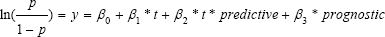
With

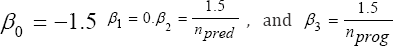
where

n_pred = n_prog = 15

Thus, the model for generating the LR patients in the SOC group was y = β₀ + β₃ * prognostic and for the HR patients in the TRT group was y = β₀ + β₁*τ+β₂*τ*predictive . The models for generating other subgroups were similar. For the SOC group, the expected probabilities of positive outcome for the responder and nonresponder subgroup were 0.436, for the treatment group, the expected probabilities were 0.754 and 0.436, respectively. The expected probabilities of positive outcomes are 0.436 and 0.50 for the SOC and TRT groups, respectively (Table 1). The expected power for the treatment effect is 0.344 at α= 0.05.

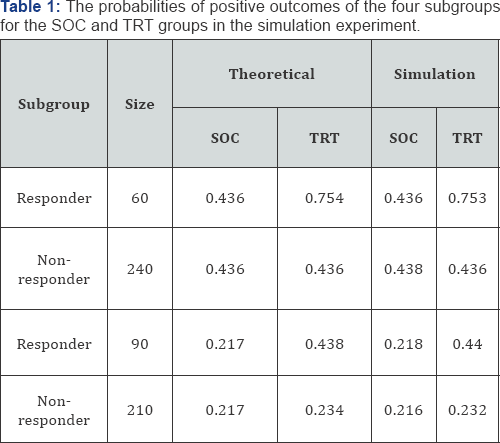
Each simulated dataset was fit to the two regression models, Eqs. (1) and (2). Table 2 shows the total number of identifications (significances) and the number of correct identifications for the biomarker sets T and U at α= 0.005 and 0.001.The model for the numbers for T and U were 15, and 25, respectively. The row for the correct identifications in U included the numbers of prognostic and predictive biomarkers correctly identified. U identified more predictive biomarkers than T.

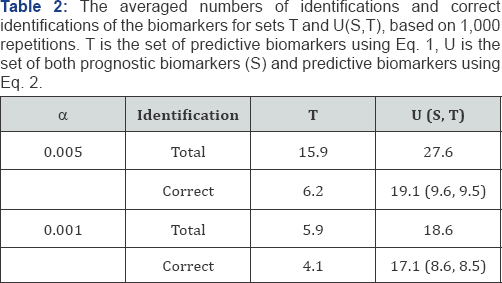
Since the specificities were high in all cases, the analyses focused on the sensitivity. For the significance levels between α= 0.005 and 0.001, the proportions of correct identifications were higher for α= 0.005; however, the proportions of true identifications were higher for α= 0.001. An explanation is that for 2,000 tests, the expected number of false positives is 10 at α= 0.005 and 2 at α = 0.001. The sensitivities were poor in T, about 40%. T identified more false positives than true positives. The analyses below will only focus on α= 0.005 since the results are similar.

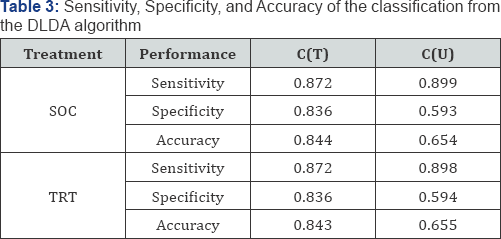
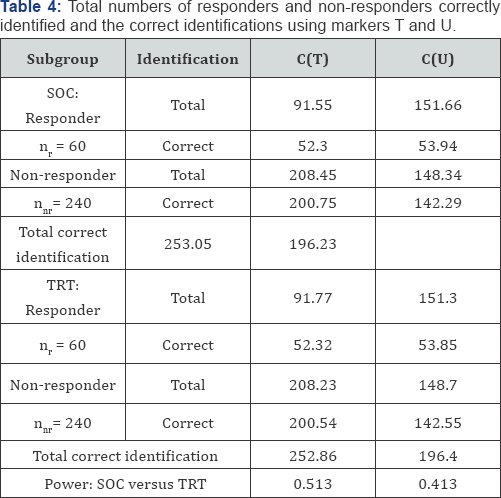
Subgroup selection: Both T and in U were used to develop the predictive classifiers C(T) and C(U), respectively. Table 3 shows the sensitivity, specificity, and accuracy for the two classifiers. The classification results for the SOC and TRT groups are very similar since the calculations were based on the test data simulated from the same model. The classifier C(U) shows good sensitivity and poor specificity due to more true positives and more false positives. Thus, when there is a treatment for all patients, the non-responder patients are likely to be classified as responders. Table 4 shows the total number of patients identified and correct number of identifications. It appears that the classifier C(T) outperformed the classifier C(U); C(U) showed too many false identifications resulting in poor specificity.

Clinical utility assessment: The expected probabilities of positive outcomes were 0.436 and 0.50 for the SOC and TRT groups, respectively. The power for detecting a treatment effect is 0.344. The probabilities of positive outcome in the responder subgroup for SOC and TRT were 0.436 and 0.754, respectively; the expected power to a detect treatment in the responder subgroup was 0.953.For the simulated data, Table 4 showed that the estimated empirical power with C(T) and C(U) were 0.513 and 0.413, respectively; both probabilities are higher than the study power 0.344. In subgroup selection, empirical power depends on subgroup sizes, effect size, and the accuracy of classification. The estimated empirical power is generally smaller than the model theoretical value since there was much false identification, partly due to random variation.

• Example

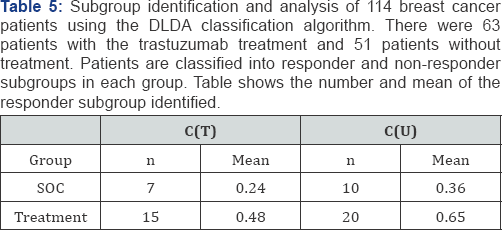
Prat et al. [30] reported an exploratory analysis of the research-based PAM50 signature to predict a response to the trastuzumab chemotherapy among breast cancer patients enrolled in the NeO Adjuvant Herceptin (NOAH) trial. The data are available from the GEO database (GSE50948). Their analysis considered 43 genes, since 7 of 50 genes did not meet the quality standard. We analyzed this dataset to illustrate an application of the proposed method. This analysis does not necessarily represent the true categorization of the patients and biomarkers. We considered only HER2+ patients in two experimental groups. The numbers of patients with and without trastuzumab treatment were 63 and 51, respectively; the corresponding observed pathologic complete responses (pCR) were 28 and 13.

Four of the 43 genes were identified as predictive biomarkers (PTTG1, FOXA1, MKI67, RRM2) by Eq. 1, and five prognostic/ predictive biomarkers (ACTR3B, RRM2, BIRC5, KRT17, MELK) by Eq. 3. Table 5 shows the numbers of patients and means of the observed outcomes in the four subgroups identified. In this dataset, the p-value for the overall test between the treatment groups was 0.058. The p-values are 0.063 and 0.051 for C(T) and C(U), respectively. The p-value from C(U) is slightly smaller that the p-value from the overall test.

Discussion

This article focuses on development of predictive biomarker- based predictive models. Two interaction models (Eq. 1 and Eq. 2) are evaluated; both models have been used to identify candidate predictive biomarkers and developed predictive classifiers C(T) and C(U), respectively. This is the first article pointing out that Eq. 2 identifies both predictive and prognostic biomarkers. The simulation shows the predictive classifier C(T) outperformed the classifier C(U). Chen et al. recently evaluated C(T) and C(U) for survival outcomes, they found that C(U) slightly outperformed C(T) in their simulations. As mentioned, accuracy of a subgroup selection procedure depends on sample size, subgroup sizes, treatment effect size, significance level, most importantly, the underlying disease and biology models. A future study to compare these two models thoroughly in terms of power and type I error in different scenarios would be helpful.

Lin & Chen [31] compared the three popular classification algorithms, RF (random forests), SVM (support vector machines), and DLDA. They showed that RF and SVM performed poorly when the class sizes differ considerably, and DLDA performed well. We, therefore, considered the DLDA classification algorithm, primarily due to imbalanced subgroup sizes, that is, many more non-responders than the responders. DLDA performs well because the decision for its boundary is based on the sample means and variances of the two subgroups, which are independent of the two subgroup sizes. More detailed discussions regarding classification of imbalanced data are given in Lin and Chen [29].

We considered only binary outcome. Subgroup selection for non-binary outcomes generally involves two steps once the candidate biomarkers have been selected. The first step is to develop mathematical models, such as Cox regression, to assign patients' predictive scores based on the biomarkers et identified. The second step is to use appropriate statistical methods to find a cutoff-point for the score and divide the patients into subgroups. For example, Li et al. [32] presented a grid search to choose the optimal cutoff that maximizes a test statistic to identify responders and non-responders. Another common approach is using classification/regression trees to partition patients into subsets of homogeneous groups [33-35]. The tree-based methods build a tree structure by simultaneously performing biomarker identification and subgroup selection in a single step.

Disease biology is complicated; the underlying genomic variables and patient population consists of several components representing different population subgroups. It is helpful to determine whether there are subgroups prior to conducting subgroup selection. Chen & Chen [36] proposed applying the likelihood ratio test (LRT) [37,38], based on the biomarkers identified, to analyze homogeneity among the sampled patients. The LRT considered the alternative model as a two-component mixture model, which may besuboptimum. We recommend that subgroup selection be conducted only when there are candidate biomarkers and the LRT is significant.

There are challenges in developing a classification model to identify patient subgroups where the genomic and target variables are random variables of observed experimental outcomes. For the binary variable considered in this article, the observed positive and negative outcomes were used as class labels to develop a binary classifier. However, positive outcomes may be non-responders, while negative outcomes may be responders. That is, some sample classes were mislabeled. Similarly, for survival outcomes there are censored observations, and long-time survival non-responders and short-time survival responders. These observed data are outliers with respect to the underlying subgroups, and the predictive models developed will be biased. Thus, when the target variable is a random variable, the developed prediction model will be prone to misclassification and bias.