Why Sub-Group Analysis is Desired to be Performed?
Sanjeev Sarmukaddam*
Maharashtra Institute of Mental Health, India
Submission: May 22, 2017; Published: June 08, 2017
*Corresponding author: Sanjeev Sarmukaddam, Research Professor, Maharashtra Institute of Mental Health, BJ Medical College and Sassoon Hospital Campus, Sangeet-Sadhana, Paramhans Nagar, Pune, Maharashtra, India, Email: sanjeev.sarmukaddam@gmail.com
How to cite this article: Sanjeev S. Why Sub-Group Analysis is Desired to be Performed?. Biostat Biometrics Open Acc J. 2017;2(2): 555581. DOI: 10.19080/BBOAJ.2017.02.555581
Abstract
The question “Is sub-group analysis desired to be performed?” is asked or raised very often. In my opinion, the answer is 'yes'. Sub-group analyses should be performed. There are few important reasons for this affirmative answer. It is important to detect subsets of patients who benefit from some of the treatments even when overall there may not be statistically significant difference in the treatments. In several types of studies we may want to examine the consistency of an observed relation across two or more subgroups of the individuals studied. For example, in a clinical trial we might want to know if the observed treatment difference is the same for young and old patients or for different stages of disease at presentation. In such cases we are interested in examining whether one effect is modified by the value of another variable. This may be viewed as the examination of the heterogeneity of an observed effect such as treatment benefit across subsets of individuals. The statistical term for heterogeneity of this type is “interaction”. The difference in 'P' values while comparing event rates or means or any other statistic, there is a temptation to claim that it establishes a difference between subgroups. However, this argument is false as a statement such as P>0.05 does not mean that 'there is no difference', merely that 'we have found no evidence that there is a difference'. A 'P' value is a combine effect of 'effect size’ (generally the difference in estimates) and 'its standard error’ (which includes, of course, sample size(s)). Therefore differences in 'P' values can arise because of differences in effect sizes or difference in standard errors or a combination of the two. Performance of 'interaction test' is must.
There are other reasons for sub-group analysis, we know that in medical/clinical research a great deal of effort is aimed at avoiding bias whenever possible and controlling for and estimating its effects when bias is unavoidable. Biases often produce the situation similar to “interaction”. Confounding is one important type of bias and one extreme example of confounding is “Simpson’s Paradox” (which occurs when the third factor reverses the apparent association between the exposures). To know whether this paradox (example: A particular risk factor may be found significant separately for males and females but the same data may not show the significance when merged) or any type of confounding was/is present in the study/trial, performing sub-group analysis is beneficial Even if some clinically expected variable is statistically not-significant, sub-group analysis may help to show that this occurance is or is not because of some bias like Simpson’s paradox.
Introduction
Patients recruited into a clinical trial are not a homogeneous sample. Their response to treatment and the differing impact on them of different treatments may well vary in ways that affect the choice of which treatment is best for which patient. Thus, if in truth there are specific subgroups of patients for which a new treatment is more (or less) effective (or harmful) than is indicated by the overall comparison with standard treatment in the trial as a whole, we have a scientific and ethical obligation to try and identify such subgroups.
But several difficulties arise while undertaking subgroup analyses. Few difficulties of these are as follows:
- Most trials only have sufficient statistical power only to detect the overall main effect that is the difference in response between treatment groups, so that if subgroup effects do exist, they may well go undetected because the trial was not large enough. Indeed, most trials could only have detected very large subgroup effects.
- Given the plethora of baseline variables and the tendency not to have a clear predefinition of which subgroup(s) may be more (or less) differentially responsive to a new treatment, there are many possible subgroup analyses that could be performed. Hence one needs to guard against data dredging and the potential for post hoc emphasis on the 'most interesting’ across many subgroup analyses.
- The most appropriate statistical methods for making inferences from subgroup analyses [namely interaction tests] are often not used in trial reports. Statistical tests for interaction, which directly examine the strength of evidence for the treatment difference varying between subgroups, are the most useful approach for evaluating subgroup analyses. Sometimes the fact that interaction tests usually lack statistical power is put forward to argue against their use. However, this is the very reason they are of great value:interaction tests recognize the limited extent of data available for subgroup analysis, and are the most effective statistical tool in inhibiting false or premature claims of subgroup findings. If the overall treatment difference is statistically significant, then it is very likely that some subgroups will and some will not show a significant treatment difference depending on chance and the smallness of subgroups.
- The extent to which subgroup analyses should affect the interpretation and conclusions in a trial report is a controversial matter. While responsible trials need to conclude whether a treatment effect (or lack of effect) is not generalizable to certain type(s) of patient, they also need to guard against making exaggerated subgroup claims that are not sufficiently robust to affect treatment policy.
Note: while compiling rates, actuaries often aggregate data from more than one source, while at the same time stratifying the data to achieve homogeneity. Such exercises may lead to biased and sometimes even surprising results, due to Simpson's paradox, because the variables involved in the aggregation process or the stratification process are confounded by the presence of other variables. Such phenomenon may also be seen in other fields.
Interaction tests
The statistical term for heterogeneity [of above defined type] is “interaction”. That is when more than one cause acts together, the resulting risk may be greater or less than would be expected by simply combining the effects of the separate causes. Sometimes, the term “biologic interaction” is used to distinguish it from “statistical interaction”. Statistical interaction is present when combinations of variables in a mathematical model add to the model's explanatory power after the net effects of the individual predictor variables have been taken into account. It is conceptually related to biologic synergy or antagonism but is a mathematical construct and may not be an observable phenomenon in nature. The statistical term interaction relates to the non-independence of the effects of two variables on the outcome of interest. Structure of such test(s), in general, is discussed with published examples below [1,2].
General
When comparing two independent estimates with standard errors, say SE1 and SE2, we can derive the standard error of the difference as 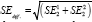 . Much the same procedure for comparing subgroups applies to all outcome measures. A confidence interval can be constructed as {Difference in estimates ± [Z1-ɑ/2 × SEdiff ]} or {Difference in estimates ± [t1-ɑ/2 × SEdiff. ]} as appropriate.
. Much the same procedure for comparing subgroups applies to all outcome measures. A confidence interval can be constructed as {Difference in estimates ± [Z1-ɑ/2 × SEdiff ]} or {Difference in estimates ± [t1-ɑ/2 × SEdiff. ]} as appropriate.
Example-1: Proportions: In a trial of antenatal steroids (i.e. treatment) for preventing neonatal respiratory distress syndrome (i.e. adverse event) was performed to see whether the effect of treatment was different in babies whose mothers are with (say group-I) and without (say group-II) pre-aclampsia. Data and relevant results are summarized in Table 1 below [1].
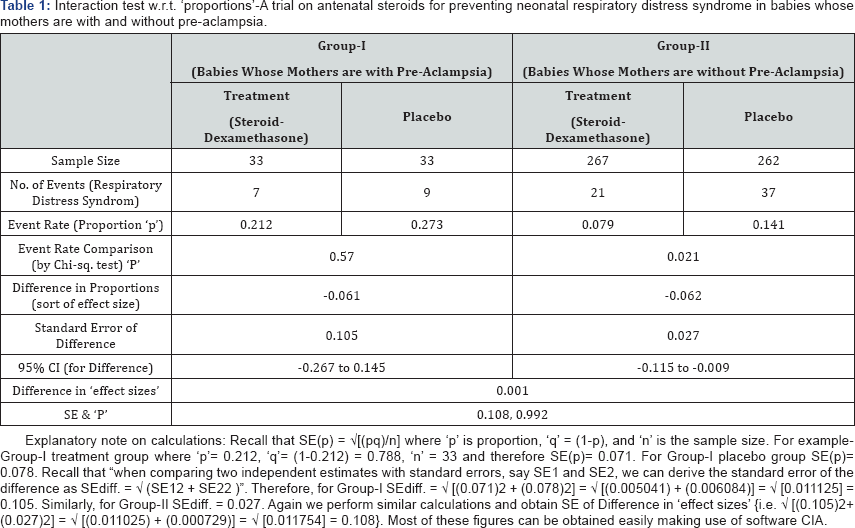
There is a temptation to claim that the difference in (Event Rate Comparison) 'P' values (0.57 & 0.021) establishes a difference between subgroups because "there is a treatment effect in mothers without pre-eclampsia but not in those with pre-aclampsia". However, this argument is false as (recall that) a statement such as P = 0.57 does not mean that 'there is no difference', merely that 'we have found no evidence that there is a difference'. A 'P' value is a combine effect of 'effect size' (generally the difference in estimates) and 'its standard error' (which includes, of course, sample size(s)). Therefore differences in 'P' values (e.g. 0.57 & 0.021) can arise because of differences in effect sizes or difference in standard errors or a combination of the two. Note that only a small proportion of mothers had pre-aclampsia (66 out of 595), so the former treatment effect is estimated much less precisely than the latter. Also note the 'overlap' in CI for 'difference'. Since the difference in 'effect size' is only 0.001 (i.e.1%) which is not significant (P=0.992) it can be concluded that there is "no interaction".
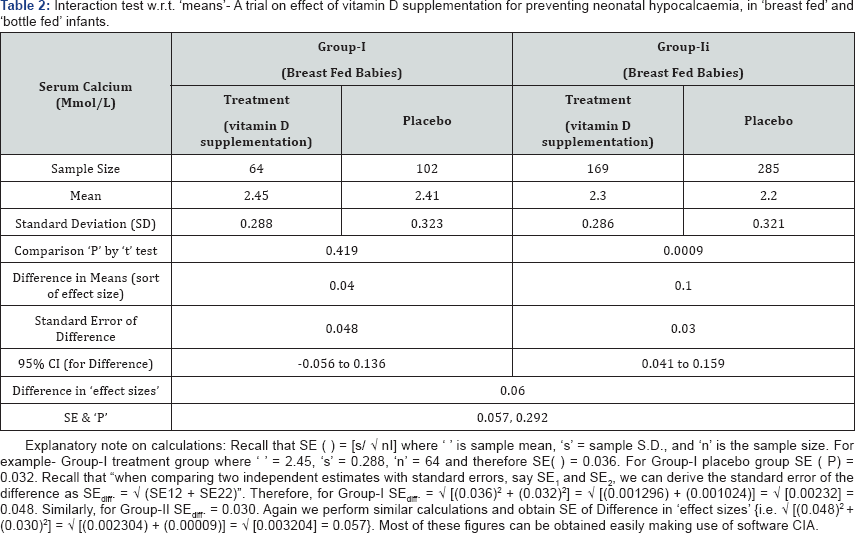
Example-2: Means: In a study of the effect of vitamin D supplementation for preventing neonatal hypocalcaemia, expectant mothers were given either supplements or placebo randomly and the serum calcium concentration of the baby was measured at one week. The benefit of vitamin D supplementation was investigated separately for 'breast fed’ and 'bottle fed' infants. Data and relevant results are summarized in Table 2 below [1].
*: Values obtained by taking "natural logarithms" of values in preceding row.
It is likely to be claimed that the difference in means by ‘t’ test yielding ‘P’ values of 0.419 & 0.0009 establishes a difference between subgroups. However, it would be wrong to infer that vitamin D supplementation had a different effect on breast and bottle fed babies on the basis these ‘P’ values. Note the ‘overlap’ in CI for the ‘difference in means’. Since the difference between the two treatment effects is 0.10- 0.04 = 0.06mmol/l with standard error 0.057 yields P = 0.292 which is not significant, it can be concluded that there is “no interaction” i.e. there is no evidence that the effect (of vitamin D supplementation) is different for the two feeding groups.
Example-3: Ratios: Here we consider comparing relative risks [3] (similar procedure is for comparing odds ratios). These measures are always analyzed on the ‘log’ scale because the distributions of log ratios tend to be closer to ‘normal’ than of the ratios themselves. Example given [3] uses the data from one meta-analysis, but it should be noted that procedure will remain same even when data are from single study. Therefore, here we just use the data (from the same paper, without consideration of source). We estimate standard errors from confidence intervals which are reported directly (without giving SEs). Trial is to study the role of hormone replacement therapy in non-vertebral fractures (where the overall relative risk was 0.73 (P=0.02) in favor of hormone replacement therapy). Data and relevant results from this trial are summarized in Table 3 below [2].
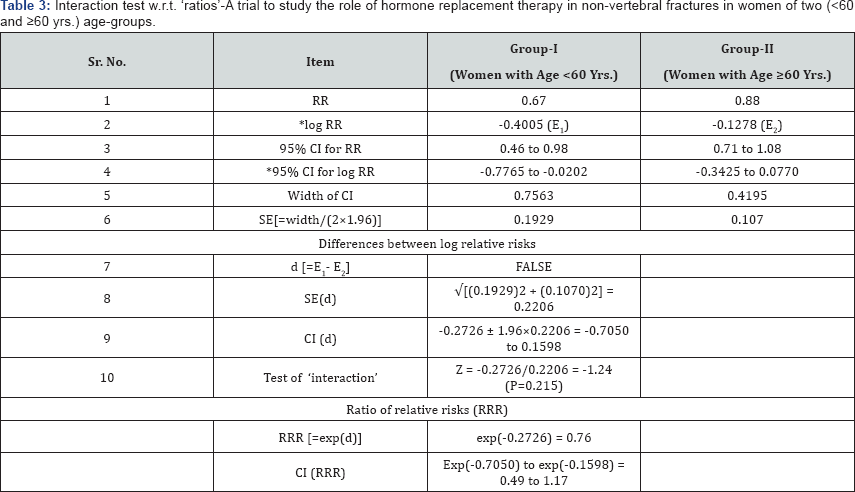
Explanatory note on calculations: All calculations are self-explanatory (i.e. figures in column 3 are obtained according to procedure given in column 2) and so there is no need of further explanation. Most of these figures can be obtained easily making use of software CIA.
It is clear from the above table that for women with age <60yrs. the relative risk was 0.67 and for women with age ≥60 yrs. the relative risk was 0.88 i.e. in younger women the estimated treatment benefit was a 33% (=100-67) reduction in risk of fracture (which was statistically significant, P=0.03, ‘P’ is not given in table) compared with a 12% (100-88) reduction in older women (which was not statistically significant, P=0.22, ‘P’ is not given in table). However the main question is ‘are the relative risks from the subgroups significantly different from each other?’ The test of interaction (which certainly answers the above question) is the ratio of ‘d’ (difference in two log transformed RRs) to its standard error i.e. Z = -0.2726 / 0.2206 = -1.24, which gives P=0.215, not significant. The estimated interaction effect is (exp (-0.2726) =) 0.76 which can also be obtained directly as ‘ratio of RRs’ (=0.67/0.88=0.76). The confidence interval for this effect is (-0.7050 to 0.1598) on log scale or (0.49 to 1.17) in relative risk scale. There is no good evidence to support a different treatment effect in younger and older women.
Even when the two estimates (say Proportions or Means or RRs or ORs) and ‘P’ values seem very different the ‘test of interaction’ may not be significant. It is not sufficient for Proportions or Means or RRs or ORs to be significant in one subgroup and not in another. Although comparing confidence intervals is less likely to mislead it is not always correct to assume that when two confidence intervals overlap the two estimates are not significantly different. For quantitative data (and means) there is a direct correspondence between the confidence interval approach and ‘t’ test of the null hypothesis at the associated level of statistical significance (i.e. resulting ‘P’ value), this is not exactly so for qualitative data (and proportions). Most of above (or discussed below) issues are described in details in the many good text books [4-7] or articles [1,2] in the specific literature on the subject (Table 1).
Enough discussion on ‘Confounding Bias’ [&/or other type of biases] can be found in many articles [8] or books [3,4] on the subject. A particular risk factor may be found significant separately for children and adults but the same data may not show the significance when merged. This special type of confounding known as "Simpson’s Paradox” (which is not a true paradox but rather a bias). Simpson’s Paradox (can viewed) as a statement about the possible effect of collapsing multidimensional tables in presence of interactions. Julious & Mullee found and published (BMJ, 1994, 309: 1480-1481) a real example of this paradox. One more example can be found in Ralf Reintjes, et al. ‘Simpson’s Paradox: An Example from Hospital Epidemiology’ Epidemiology, Vol. 11, No. 1 (Jan., 2000), pp. 81-83.
The classic illustration of the paradox involves college admissions by gender, which can be illustrated in the example in table below (Table 4). In the above table the overall acceptance ratio for female applicants, 19%, is lower than the ratio for the male applicants, 35%. However, this relationship reverses when the factor of the college to which they apply is introduced. When this variable is considered, the acceptance ratio for female applicants is 25% higher than male applicants for both the engineering college (50% to 40%) and the medical college (13% to 10%).

The reason why Simpson’s paradox occurs is that more female applicants apply to the medical college, which has an overall lower acceptance rate than the engineering college. The engineering college has a 40% to 50% acceptance rate, while the medical college has a 10% to 13% acceptance rate. In the above example, about 83% of female applicants apply to the medical college, while 83% of male applicants apply to the engineering college (Table 2).
Cates [9] considers “how should we pool data?”, focusing in particular on the calculation of the number needed to treat (NNT). He explains how Simpson's paradox may lead to the wrong answer when the NNT is calculated in a particular way. To summarize in statistical/mathematical notations:
Simpson's Paradox
It is possible to have P (A/B) < P (A/B') and have at the same time both
P (A/BC) ≥ P (A/B ‘C) & P (A/BC') ≥ P (A/B'C').
Hypothetical Example:
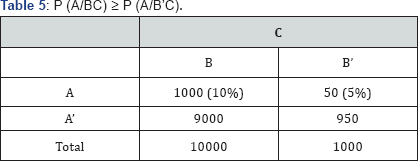
i) P (A/BC) ≥ P (A/B'C) (Table 5)
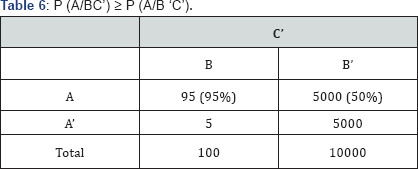
ii) P (A/BC’) ≥ P (A/B ‘C’)(Table 6)
iii) P (A/B) < P (A/B’) (Table 7)
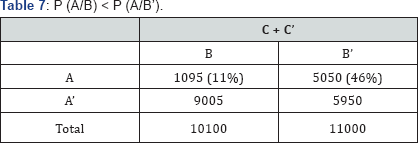
The marginal table, adding over the third variable. Odds ratio for the marginal table (Table 3) is 0.14 which is significantly lower than one. Odds ratio in each layer separately (corresponding to levels of the third variable ‘C’) are 2.11 (Table 1) and 19.00 (Table 2) respectively, which are significantly higher than one.
References
- Hanson MA (1993) Second order invexity and duality in mathematical programming. Opsearch 30: 313-320.
- Mond B, Weir T (1981) Generalized concavity and duality. In: Schaible S & Ziemba WT (Eds.), Generalized Concavity in Optimization and Economics, Academic Press, New York, USA, pp. 263-279.
- Yang X (1994) Generalized convex duality for multi objective fractional programs. Opsearch 31: 155-163.
- Dinkelbach W (1967) On nonlinear fractional programming. Management Sci 13: 492- 498.
- Verma RU, Zalmai GJ (2016) Second-order parametric optimality conditions in discrete minmax fractional programming. Communications on Applied Nonlinear Analysis 23(3): 1-32.
- Verma RU, Zalmai GJ (2016) Second order parametric optimality conditions in semi-infinite discrete minmax fractional programming based on second-order sonvexities. Transactions on Mathematical Programming and Applications 4(1): 62- 84.
- Zalmai GJ (1989) Optimality conditions and duality for constrained measurable subset selection problems with minmax objective functions, Optimization 20: 377-395.
- Zalmai GJ (2012) Generalized second-order (F,β,φ,ρ,θ)-univex functions and parametric duality models in semiinfinite discrete minmax fractional programming, Advances in Nonlinear Variational Inequalities 15: 63-91.
- Zalmai GJ, Zhang Q (2007) Generalized (F,β,φ,ρ,θ)-univex functions and global parametric sufficient optimality conditions in semiinfinite discrete minmax fractional programming, Pan American Mathematical Journal 17: 1-26.






























