Biostatistics and Biometrics Open Access Journal

Short Communication

The Device for Lowering of Insulin in the Blood with Use of Infrared Radiation and Porous Tini Alloy

Gunther S¹*, Dambaev G², Kang JH³ and Gunther V¹

¹Tomsk State University, Research Institute of Medical Materials, Russia

²Siberian State Medical University, Department of Clinical Surgery, Russia

³ Kang & Park medical, South Korea

Submission: May 23, 2017; Published: June 05, 2017

*Corresponding author: Gunther S, Tomsk State University, Research Institute of Medical Materials, Russia, Email: guntersv@inbox.ru

How to cite this article: Gunther S, Dambaev G, Kang J, Gunther. The Device for Lowering of Insulin in the Blood with Use of Infrared Radiation and Porous Tini Alloy. Biostat Biometrics Open Acc J. 2017;2(1): 555580. DOI: 10.19080/BBOAJ.2017.02.555580

Abstract

Several classes of generalized higher order parametric sufficient optimality constraints for a discrete minmax fractional programming problem are investigated toward establishing advanced results on higher order fractional programming. These results are established by applying advanced partitioning schemes and various types of generalized second-order (F,β,Π,φ,ρ,θm)-univexity assumptions. The obtained results are new and generalize most of the results on (F,β,φ,ρ,θ)-univexity in the literature.

Keywords: Discrete minmax fractional programming; Second-order univex functions; Generalized sufficient optimality conditions

Short Communication

The main objective in diabetes treatment is to reduce the blood sugar level to the normal one. Numerous studies show that diabetes prevalence is increasing every year regardless of the age, gender and ethnicity.

The most common currently used method of diabetes treatment is intradermal insulin injections. This method causes mechanical trauma, pain and psychological discomfort. In addition, it may result in allergic reactions observed in both the local area of high drug concentration and the whole organism.

Today, researchers take great interest in the development of new methods of insulin delivery that provide a long (prolonged) effect. This is caused by the need to release the patient from the necessity of frequent injections of short action insulin (3-4 times a day). Each injection is associated with a negative emotional response to pain as well as specific difficulties of compliance with conditions of asepsis and antisepsis. One of the tendencies related to this problem is development of methods providing needle-free insulin delivery in the human organism. New methods of insulin delivery (orally or inhaled) are being actively developed.

The most promising method is needle-free injection of insulin using porous TiNi alloys and IR radiation. The development of the powder metallurgy and self-propagating high temperature synthesis (SHS) in a combustion mode gave rise to a new class of highly permeable TiNi-based materials (Figure 1). These materials can hold fluid media in the pore space, including insulin solution. Due to the capillary effect, diffusion processes under IR exposure, the solution can be hold in the porous TiNi volume and the liquid can be directionally released from the pores [1-3].

The analysis of interaction of porous permeable TiNi-based alloys with various tissue fluids of the organism showed the efficiency of these materials as capacitive medical materials. High-capacitive devices for effective needle-free delivery of insulin solution into the tissue system of the organism can be developed due to a wide range of physical-mechanical properties of TiNi alloys and the possibility of producing porous structural elements. In addition, these alloys exhibit high intensity of heat transfer at low level of thermal conductivity [2,4].

The IR sources that regulate diffusion make the basis for the design of these devices and porous permeable TiNi elements. When the porosity of TiNi ranges from 60% to 70%, the insulin solution can take more than half of the volume of the capacitive construction element. The process of insulin diffusion of porous permeable of TiNi matrix depends on numerous factors, such as insulin viscosity, specific weight, density, permeability, pore length and size, the surface contacting with the environment, temperature of the porous matrix and others. The formula shows the dependence of the rate of change in the liquid volume of the TiNi porous structure on basic parameters of the insulin solution diffusion.

IR radiation can be used to change the temperature parameter .ΔT (temperature gradient). It allows control of the rate of the insulin solution diffusion relative to the power, wavelength and duration. IR radiation in the range from 800 to 1100 pm has a distinct thermal effect that causes excitation of thermo receptors in the skin, mucous membranes and cornea, and in the central nervous system (spinal cord and hypothalamus). This radiation penetrates up to 2cm deep in the body tissue. The penetration depth depends on both the wavelength and the moisture content in the skin, blood content, degree of pigmentation and other individual factors [1,3,5].

The impulses from thermo receptors travel into the thermoregulatory centers (hypothalamus and partially spinal cord). Further, the thermoregulation reactions cause expansion of the skin vessels and increase the volume of the blood circulating in the vessels, which results in increased sweating. Nerve-reflex reactions occur also under IR irradiation of the reflexogenic areas of the skin segments, which are connected with the internal organs. IR irradiation of the tissue leads to formation of biologically active substances such as bradykinin, kallidin, etc. These substances are wcrucial for humoral reactions of blood circulation (local and general).

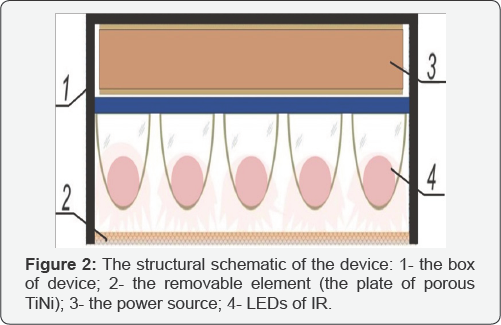
Small and medium doses of IR radiation increase metabolism accelerate cell reproduction and enzymatic reactions that stimulate regeneration processes. Figure 2 presents a schematic structure of the device for needle-free delivery of insulin solution in the tissue system of the body and figure 3 shows its practical use. To prepare the device for work, the battery is charged, the element is saturated (a plate of porous permeable TiNi alloy) with insulin solution. Then, the device should be fixed to the wrist (like a bangle). The porous element should be in contact with the skin and IR LEDs are turned on. The L-53SF6C type LEDs with wavelength λ= 920nm and power of 120mW by King bring were used as IR sources. The device is supplied with a Li- ion battery with capacity of 640mA and total weight of about 50g.

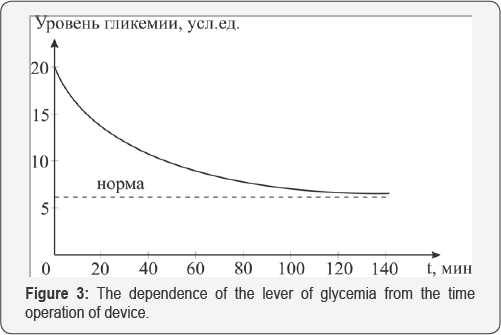
This device converts electrical energy into thermal energy to make a system of soft heat thermo mechanical IR effect. The procedure time (30-120min) depends on the change in the blood glucose level. Glycemia (Figure 3) decreases monotonically within the first 30min and then it is followed by gradual slowdown within the next 30min and reaches its steady-state level 120min after the start of the procedure [3]. Nowadays, the main goal in the treatment of diabetes is to reduce glucose in the blood. The modes of insulin introduction simulating a natural dynamic of its concentration have been used for this purpose.

The insulin secretion in healthy patients is discrete during the day. The discrete character of the secretion caused by increased blood glucose facilitates the constant release of insulin from the pancreas. The introduced long-acting insulin creates "simulated" basal secretion of insulin. The introduction of the short-acting insulin 30min before a meal creates an additional rise of insulin in the blood, which coincides with hyperglycemia in time. Sometimes, good results can be obtained if insulin is introduced at a fixed time, but the reliable data on the discrete introduction of insulin is not reported in the scientific literature. Thus, the use of IR radiation and porous permeable TiNi (MoFe) opens the perspective for development of new needle-free devices.