On Unifying Concepts of Epidemics and Systemic Risk
E Ahmed1* and HAA El Saka2
1Department of Mathematics, Mansoura University, Egypt
2Department of Mathematics, Damietta University, Egypt
Submission: March 6, 2017; Published: April 21, 2017
*Corresponding author: E Ahmed, Mathematics Department, Mansoura University, Egypt, Email: magd45@yahoo.com
How to cite this article: E Ahmed, HAA E S. On Unifying Concepts of Epidemics and Systemic Risk. Biostat Biometrics Open Acc J. 2017;1(2): 555559. DOI: 10.19080/BBOAJ.2017.01.555559
Abstract
Two unifying concepts of epidemics and systemic risk are given. The first is super spreaders. The second is population heterogeneity.
Introduction
Systemic risk is the one where the failure of one bank causes the failure of several connected ones. This is similar to percolation. There are two beliefs [1] that a given bank is too large to fail and a given bank is too well connected to fail. This means that nodes [2] in inter-banks networks are not similar. There are large banks and there are small ones. Large banks are more relevant to systemic failure than small ones. In this letter two unifying concepts of epidemics and systemic risk are given. The first is super spreaders. The second is population heterogeneity.
Super Spreaders
Here we give a mean field network model for systemic risk. It contains two types of interactions local and non-local [3]. The non-local is only for large banks. We assume that every group of small banks is connected to a large bank. The existence of these two types of interaction is an advantage to this approach. Another advantage is when a large bank gets in trouble it has two states: In the first it does not propagate its problems to others (infected but non-infectious). In the second state it becomes both infected and infectious. Let p1 (p2) be the probability of local (non-local) transmission of a troubled state. Let r0 be the probability that an infected but non-infectious bank become infectious. Let r1 be the probability that an infectious bank recovers. Let m be the expected number of nonlocal neighbors and let n(i) be the number local neighbors of node i. Thus an intuitive condition for the systemic risk to be contained is
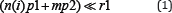
The probability that systemic failure will not propagate in the whole of the network is [3]
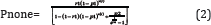
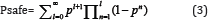
Where p = Pnone is given by Eq. (2).
Now we can comment on the following statements [4]:
Too large to fail disagree with (1) since it means large m.
Too well connected to fail disagree with (1) since it means large n(i).
This agrees with the fact that in the 2008 crisis some large banks have failed.
A proposition [5] is given to break large banks. We think this is difficult to apply.
Population Heterogeneity
Systemic risk is quite similar to epidemics on heterogeneous population [6,7]. It was shown that the condition for disease spread (systemic failure) is [6]:
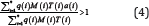
Where a(i)=q(i)R(i)/[1-p(i)R(i)], q(i)=1-p(i), i=1,2,...,n are the different subpopulations, p(i) is the portion of group i that contacts specifically to their subgroup (local interaction), T(i) is the number of susceptible individuals in group i, M(i) is the mixing rate of group i and R(i) is the reproduction number of group i.
Conclusion
In conclusion the authors would like to note that this model is a great oversimplification and lacks many features of real economy. However, it must be kept in consideration that the complexity of real economy is such that constructing a model which can be used for quantitative prediction, is a task oftremendous difficulty. A real economy is a tremendously complex system that depends on a very large number of parameters and can be influenced by a vast variety of factors. Many of these factors and parameters are unknown or even in principal unmeasurable. One hardly can expect that a precise or reasonably accurate quantitative description for such a process is feasible. Under such circumstances, constructing and exploiting a simple conceptual model that is aimed at qualitative description rather than at obtaining precise quantitative predictions, is well justified.
References
- Haldane AG, May RM (2011) "Systemic risk in banking ecosystem” Nature 469(7330): 351-355.
- Lehnert J (2016) "Controlling synchronization in patterns complex networks”, Springer.
- Small M, Tse CK, Walker M (2006) "Super-spreaders and the rate of transmission of the SARS virus”, Physica D 215: 146
- Wikipedia Systemic risk.
- Mertzanis C (2014) "Complexity Analysis and Systemic Risk in Finance: Some Methodological Issues”. Network Models in Economics and Finance Springer 100: 199-237.
- Dushoff J, Levin S (1995) The effects of population heterogeneity on disease invasion, Math Bio Sci 128(1-2): 25-40.
- Macacu A, Bicout DJ (2017) Effect of the epidemiological Heterogeneity on the Outbreak Outcomes, Math Biosci Eng 14(3): 735-754.






























