Mini Review

Features of the Laws of Wave Reflection and Refraction at the Mobile Interface

Glushchenko AG*

Department of Physics Povolzhsky State University of Telecommunications and Informatics, Samara, Russia

Submission: June 17, 2024; Published: July 03, 2024

*Corresponding author: Alexander Glushchenko AG, Department of Physics Povolzhsky State University of Telecommunications and Informatics, Samara, Russia

How to cite this article: Glushchenko AG. Features of the Laws of Wave Reflection and Refraction at the Mobile Interface. Ann Rev Resear. 2024; 11(3): 555814. DOI: 10.19080/ARR.2024.11.555814

Annotation

The Doppler Effect is one of the fundamental laws of physics and has found wide application in various fields of measuring and functional technology. It consists in changing the frequency perceived by the receiver from the radiation of the source of oscillations when they are mutually displaced. In practice, uniform displacement of the emitter and receiver is usually considered. This paper examines a type of the Doppler Effect during the reflection and transmission of waves through a moving interface between two isotropic media. It has been established that the movement of the interface leads to anisotropy of the structure and a change in the known laws of reflection and refraction. The angles of reflection and refraction of waves become dependent on the speed of movement of the interface between the media. At the same time, a change in the frequency of the waves reflected and transmitted through the interface is observed. Analytical calculated relations are obtained for the angles and for the frequencies of waves reflected and transmitted through the boundary, which transform into known relations for a stationary interface. It has been established that the reflection and transmission coefficients do not depend on the speed of movement of the interface. Formulas are obtained for calculating the angles of total internal reflection and Brewster angles, taking into account the velocity of the boundary. The conditions have been established under which the effect of negative refraction, characteristic of refraction at the boundaries of optically negative media, occurs.

Keywords: Lipid Profile; Sickle Cell; ABO; Blood Groups; TG; HDL; LDL

Abbreviations: ANOVA: Analysis of Variance; SCD: Sickle Cell Disease; HbS: hemoglobin S; SCA: Sickle Cell Anemia; RBCs: Red Blood Cells; VOC: Vaso-Occlusive Crisis; ACS: Acute Chest Syndrome; OTN: Osteonecrosis; TG: Triglycerides; TC: Total Cholesterol; HDL: High Density Lipoprotein; LDL: Low-Density Lipoprotein; LDL-C: Low Density Lipoprotein-Cholesterol; HDL-C: High Density Lipoprotein-Cholesterol; apo A: apolipoprotein A; apo B: apolipoprotein B; VLDL: Very Low-Density Lipoprotein

Introduction

When objects moving relative to each other interact, a change in the frequency of their interaction is observed (the Doppler Effect, which has a kinematic origin) [1,2]. The magnitude of the frequency shift of waves reflected and transmitted through the interface depends on the ratio of the relative speed of movement of objects and the speed of waves in the medium [2,4]. The widespread use of this physical effect in acoustics and optics determines the high attention paid to this physical effect [5-7]. Recently, there has been increased interest in the Doppler effect [8,9] due to the discovery of new possibilities for its use in various fields of optics, microwave [3] technology, technical acoustics of its various varieties: anomalous [9], reverse, transverse, double, parametric [7,8], complex, rotational [10,11], nonlinear, during the interaction of radiation with anisotropic media [12,13], meta media and negative [14] media, experimentally recorded in the optical range. Measurements of the Doppler redshift of lines in the emission spectra of galaxies led to the construction of a model of the structure and dynamics of the Universe [2].

Historically, the Doppler Effect was first well and clearly described by geometric models, the simplicity and clarity of which attracts the authors of many studies. However, the capabilities of geometric models are limited to the simplest configurations [1,2]. The influence of various factors: the movement of interfaces between media, the movement of the media themselves, accompanied by the entrainment of wave processes by them, determines the feasibility of a more rigorous analysis of the effect of reflection from moving boundaries of areas based on the theory of wave processes of any physical nature (electrodynamics, acoustics, etc.) [1,6]. In this work, using the methods of wave theory [3,4], the features of the reflection and transmission of waves of a moving interface between media are considered. It has been established that a change in the frequency of waves reflected and transmitted through the moving boundary leads to a change in the laws of reflection and refraction, which, as analysis shows, also depend on the speed of movement of the interface between the media until the appearance of the effect of negative refraction, characteristic of optically negative media (moving interface the medium behaves under certain conditions as an optically negative medium). It has been established that the magnitude of the reflection and transmission coefficients does not depend on the state of motion or rest of the interface between the media.

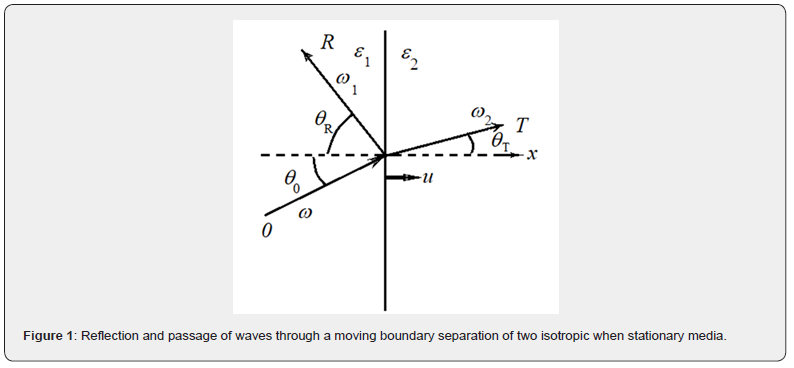
Model for research. We consider the reflection of waves from the moving boundary of a layer of two magnetodielectrics 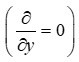that are isotropic in a stationary state (Figure 1). Let the interface between homogeneous two media with both refractive indices 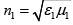and refractive index 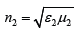move at a constant speed u along the 0x axis. The coordinate of the interface is described in time in the general case by the dependence . In particular, for the uniformly variable speed of movement, considered by Ritz [15] . The speed of propagation of waves in a stationary medium is equal to 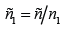, in the second , where c is the speed of light in vacuum. To analyze the features of the reflection of electromagnetic waves incident from region 1 on the surface of the moving layer 2, and the passage of waves into region 2, let us consider H (Hx, Ey, Hz) waves.

The wave equations in regions 1-2 have the form:

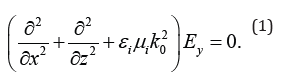
the boundary conditions at the moving interface (x = ut) have the form [3,4]:

Due to the Doppler Effect, an analytical solution is sought in the form of incident, reflected and transmitted waves with different frequencies:

where ω₀ is the frequency of the incident wave ω_R, is the frequency of the wave reflected from the boundary of the moving layer in the first medium ω_T, is the frequency of the wave transmitted to the second medium. In general, the wave numbers of the forward and backward waves in the first medium and the forward wave in the second medium are different: 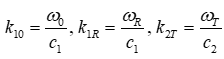. The first boundary condition must be satisfied for any moment in time, which leads to the relationship between the frequencies of the incident, reflected and transmitted waves in the form:

When the boundary moves (u ≠ 0), the frequencies of the direct, reflected and transmitted waves differ.

Basic Results and Discussion

From (5) it follows that the frequency ω_R of the wave reflected from the moving layer is determined through the frequency ω0 of the wave incident on the boundary by the relation

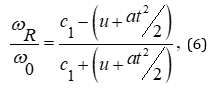
In the general case, the angle of reflection and the angle of incidence are not equal to each other, and with uniform motion of the boundary, their ratio depends on the speed of motion u, and with accelerated motion, on acceleration and changes in time. The projections of wave numbers onto the 0z axis are equal to:

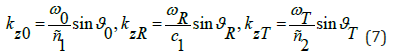
Since the boundary conditions must be satisfied at any point z, then

those the angle of incidence and the angle of reflection are related by the relation

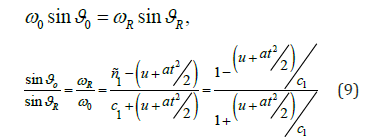
which at 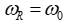i.e. in the absence of the Doppler effect 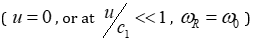and with acceleration equal to zero, it transforms into the known relationship: 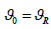(the angle of reflection is equal to the angle of incidence).

In the presence of the generalized Doppler Effect, the angle of reflection is not equal to the angle of incidence and the relationship between them depends on the speed of movement of the interface between the media, acceleration, and changes with time.

The dependence of the angle of reflection on the parameter of the relative speed of movement of the interface is shown in Figure 2, from which it can be seen that the angle of reflection is equal to the angle of incidence only for a stationary interface (u=0, a=0). When 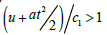(the speed of the boundary is greater than the speed of the wave), a negative ratio of the sine of the angle of incidence and reflection is obtained (negative angle of reflection, the wave is reflected in the same direction from which the incident ray came).

The greatest deviation of the angle of reflection from the angle of incidence is observed when the boundary moves in the opposite direction 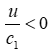. The relationship between the angles of incidence and refraction has the form

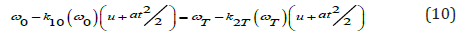
Then

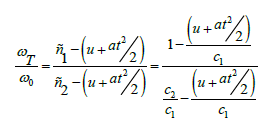
If the parameters of the adjacent media are the same 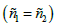, then in the second medium the wave frequency does not change 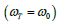. Parameters 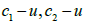play the role of refractive indices of media. The law of refraction takes the form:

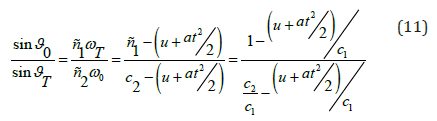
Then, with acceleration equal to zero, the angle of refraction is equal to

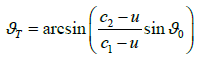
A graph of the dependence of the refraction angle on the relative speed of the boundary movement at a ratio of wave velocities in the media equal to is shown in Figure 3 at different angles of incidence The smallest dependence on the parameter 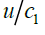is observed at small angles of incidence.

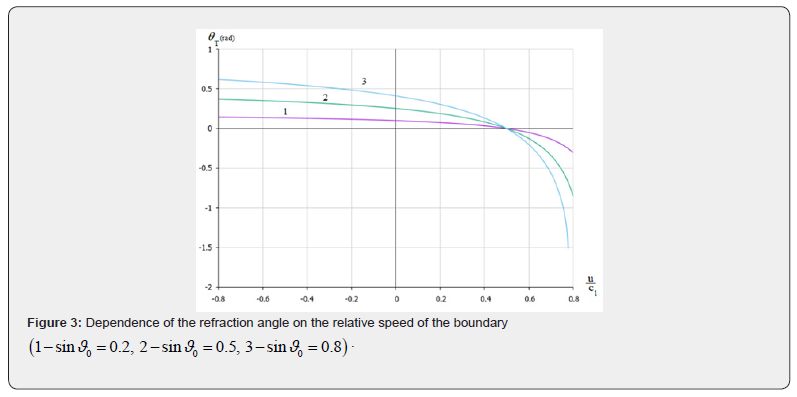
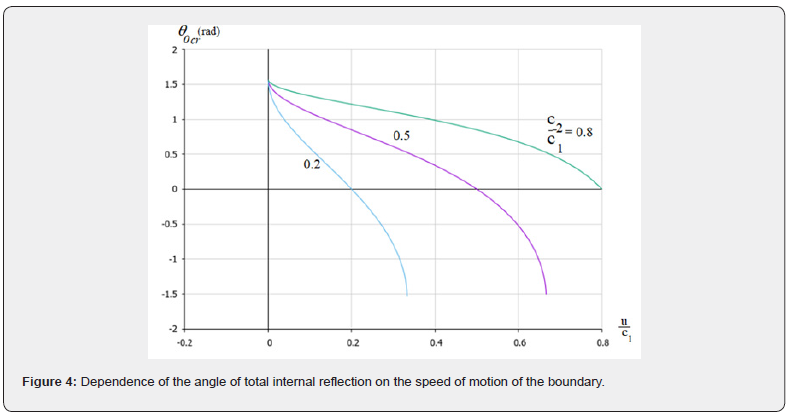
It is characteristic that if the speed of movement of the boundary exceeds the speed of movement of waves in the second medium, negative refraction can be observed at the boundary, as at the interface between optically negative media [15]. In the region 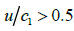negative refraction angles are observed. For the angle of total internal reflection 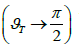we have the following relation:

In Figure 4 shows its dependence on the relative velocity of the interface. At a high speed of motion of the boundary, the angle of total internal reflection changes sign, the wave is carried away by the interface and does not pass into another medium. This effect can be recorded experimentally for acoustic signals, for which this condition can be relatively easily ensured.

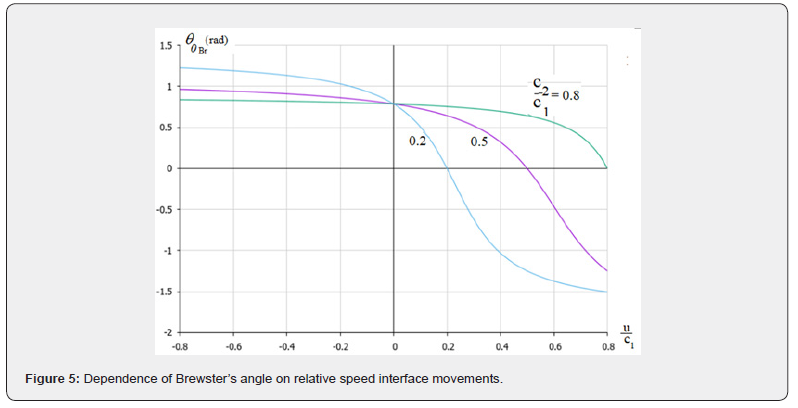
The Brewster angle (the angle of total polarization for the reflected beam) is determined by the relation: 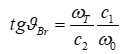whence

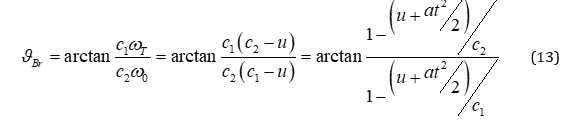
In Figure 5 its dependence on the relative velocity of the interface is shown. At high interface velocities , the angle of total polarization changes sign.

Thus, both the limiting angle of total internal reflection and the angle of total polarization at moving interfaces between media depend on the speed and direction of motion of the boundary.

Substituting the required solutions into the boundary conditions for the field components Ey, Hz at x = ut gives the relationship between amplitudes and frequencies:

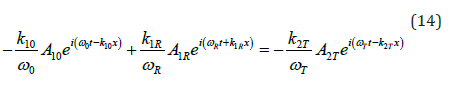
Then the reflection coefficient:

and transmission coefficient:

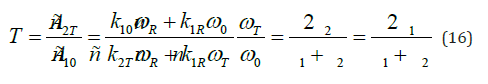
do not depend on the parameter of motion of the interface between the media and depend only on the ratio of wave velocities in the media or on the refractive indices of the media (Figure 6).

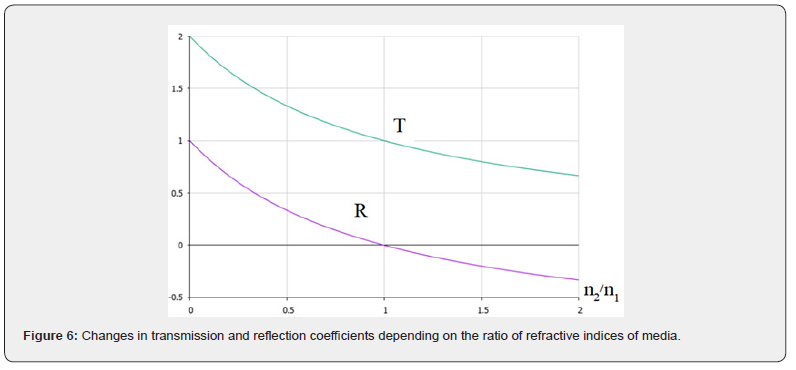
When passing through the value , the reflection coefficient changes sign (reflection changes character, reflection from a denser medium changes to reflection from a less dense medium, and a phase jump by π is observed). The transmission coefficient becomes less than one T<1.

If the interface moves in the direction of propagation of the incident wave (velocities u and c1 coincide in direction), then the frequency of the reflected signal is less than the frequency of the incident wave 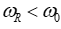; if the boundary moves towards the incident wave, then 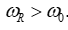. For a transmitted wave, a decrease or increase in the frequency of the Doppler shift depends on the ratio of the velocities of wave propagation in the first and third media and, if the wave velocities in these media coincide, the Doppler shift for transmitted waves is not observed.

The change in the frequencies of reflected and transmitted waves of various physical natures depends on the speed of movement of the interface between the media and the speed of the waves in the media themselves. This effect is most pronounced at speeds of movement of inhomogeneities and media comparable to the speed of wave propagation. For electromagnetic waves in these media (Figure 2 & 3), these effects manifest themselves when interacting, for example, with a flow of relativistic electrons, or with the inhomogeneity of the medium formed by wave pulses, including superluminal ones, the speed of which in the active medium can exceed the speed of light.

Conclusion

The frequency shift in the Doppler Effect depends on the speed and acceleration of the moving layer, on the speed of wave propagation in the adjacent media. At moving interfaces, the Doppler Effect can be observed due to the speed of movement of the interface and the Ritz effect due to the acceleration with which this boundary moves. The frequency shift of the reflected and transmitted waves corresponds to a change in the angles of reflection and refraction, stationary due to the Doppler Effect and changing over time due to the Ritz effect. For a refracted wave, a change in the refraction angle is observed up to negative values, previously noted in optically negative media. The movement of the interface leads to changes in the angles of total internal reflection and the angle of total polarization. In this case, the angle of total internal reflection can take negative values, which corresponds to the drift of the incident wave by the interface and the absence of a refracted wave. With accelerated movement of the boundary, these effects become dynamic and limited in time by the actually limited increase in the speed of the boundary. The data that support the findings of this study are available within the article.

References

1. Seddon N (2003) New look for the Doppler Effect. Sci 302: 1537.
2. Schuster P (2005) Moving the Stars. Christian Doppler, His Life, His Works and Principle and the World After. Living Edition Publishers pp. 232.
3. Collin RE (2000) Foundations for Microwave Engineering/ RE Collin - (2^nd Edition) Wiley-IEEE Press pp. 944.
4. Glushchenko AG, Glushchenko VA, Glushchenko AA (2024) Generalized Doppler Effect in Wave Interaction with Uneven Moving Boundaries of Mobile Environments. Biomed J Sci & Tech Res 56(2).
5. Lazarev Yu F (2011) Signal delay and the Doppler Effect. Bulletin of NTUU, Kyiv Polytechnic Institute Instrumentation Series 41: 168-179.
6. Gorban II (2004) Reflection and refraction of acoustic rays at the moving interface of media. Acoustic Herald 7(2): 36-41.
7. Rozanov NN (2012) Subluminal and superluminal parametric Doppler effects when light is reflected from a moving smooth inhomogeneity of the medium. JETP 6(12): 1101-1107.
8. Rozanov NN (2012) Superluminal parametric Doppler effect in dielectrics and in electron-positron vacuum. Letters to JETP. 95(12): 689-692.
9. Kuzelev MV, Rukhadze AA (2005) Anomalous Doppler effect and stimulated Cherenkov Effect in a plasma waveguide with a thin tubular electron beam. Plasma Phys Rep 31: 638-645.
10. Dholakia K (1998) An experiment to demonstrate the angular Doppler effect on laser light. Am J Phys 66: 1007-1010.
11. Korech O (2013) Observing molecular spinning via the rotational Doppler Effect. Nature Photon 7: 711-714.
12. Barsukov КA (1995) The Doppler Effect in chiral media. Proceedings of the 1995 International Symposium of electromagnetic theory, St. Petersburg pp. 239-241.
13. Barsukov KA (1959) About the Doppler Effect in an anisotropic and gyrotropic medium. JETP 5: 1485-1491.
14. Veselago VG (1967) Electrodynamics of substances with simultaneously negative values of ε and µ. Adv Phys Sci 92(7): 517-526.
15. Semikov S (2010) Ballistic theory of Ritz and the picture of the universe. Nizhny Novgorod. Stimul ST pp. 613.