Radian Belu

doi:10.19080/ARR.2024.10.555796

Review Article

Microgrid Optimal Power Scheduling for Grid Resilience Improvements

Radian Belu*

Professor of Electrical Engineering, Southern University and A&M College, Baton Rouge, USA

Submission: February 23, 2024; Published: March 01, 2024

*Corresponding author: Radian Belu, Professor of Electrical Engineering, Southern University and A&M College, Baton Rouge, USA

How to cite this article: Radian Belu*. Microgrid Optimal Power Scheduling for Grid Resilience Improvements. Ann Rev Resear. 2024; 10(5): 555796. DOI: 10.19080/ARR.2024.10.555796

Abstract

The adverse effects of extreme events, such as natural hazards extreme weather, or man-made contingencies on the electric grid are resulting in growing demands to address grid resilience, reliability, faster service restoration, or to provide power supply for emergency services. A microgrid, a local power system covering a small geographical area, is less vulnerable to such events and can provide emergency power. Through its features, such as local electricity generation, optimal load and power generation scheduling or islanding operation capability can significantly increase system reliability and resilience, while being able to provide power in the emergency. Optimized generation scheduling and energy management models are implemented by using simplified models of the microgrid components, composite load models, and load prioritization algorithms.

Keywords: Microgrid; Natural hazards; Extreme weather; Man-made contingencies; Energy storage systems; Diesel generators

Abbreviations: RES: Renewable energy systems; MG: Microgrid; DGs: Distributed generation; ESSs: energy storage systems; STC: Standard Test Conditions; LPSP: Loss of power supply probability; LPS: loss of power supply

Introduction

Maintaining power system reliability is one of the main concerns and objectives of any electric utility [1-8]. The adverse effects of extreme events, e.g. natural hazards, extreme weather, or man-made disruptions on the electric grids resulted in growing demands to address and enhance grid resilience, reliability, or to provide electricity for the emergency and essential services. Natural hazards, extreme weather, or man-made contingencies can severely affect the operation of the power systems with greater severity in the future smart grid due to extended communication, monitoring, and presence of the sensitive equipment [1-12]. The adverse effects of such high-impact low-probability events on the power grid resulted in growing demand to address power system resilience, provide electricity for emergency services, if needed and fast grid restoration, when such events happened. However, extreme weather is one of the main causes of power outages, having significant effects on the electrical infrastructures, with even a greater impact on the power distribution, such as extended outages and significant economic losses that can lead to large-scale and longer service interruptions impeding the post-disaster relief efforts, affecting the deployment and operation of the first-response units and recovery operations. A microgrid covering a small geographical area is less vulnerable to such events. A microgrid, consisting of distributed energy resources and renewable energy systems (RES) can provide energy to at least critical loads in a sustainable way.

A microgrid (MG), a group of local distributed electric generators, energy storage units, interconnected loads with control and management can operate in grid connected mode or disconnected from the grid (standalone or islanded operation mode) [8-17]. One of complementary valuable functionalities of microgrids, besides reducing the pollutant emissions and costs, or improving grid efficiency is to improve power system resiliency via local supply of loads and curtailment reduction. It appears to the grid as a single controllable entity, consuming or supplying power depending upon its total generation and load demands. It is also considered a key smart grid component, allowing integration of distributed generation (DGs) units, renewable energy sources, and energy storage systems (ESSs) into power distribution systems and hence removing the need for power system expansion. Such local generation, optimal load and power scheduling or islanding operation can increase system reliability, resilience while providing power in emergency, at least to essential and critical loads. Optimized generation scheduling and energy management models are implemented by using simplified MG components, composite load models, and load prioritization. Resiliency represents the power system ability to withstand low probability high impact events in an efficient manner while ensuring the least possible supply interruptions and enabling a quick recovery and restoration to the normal operation state. A novel and viable solution to resiliency issues in power systems is to deploy and/or to ad-hoc create microgrids when extreme events are taking place. A power distribution system is resilient if it can anticipate, adapt to, or rapidly recover from disruptive events, such as natural hazards, extreme weather, and humaninduced disruptions [1-8,12-17].

Simplified Microgrid Component Models, Optimal Generation Scheduling

A microgrid has key advantages, in terms of resiliency in its ability to operate in island mode, or to activate and de-activate components, which provides operational flexibility and reduces the vulnerabilities of the centralized generation and long transmission. In islanded operation mode, the loads depend upon the local MG generation [12-18]. In the case when DG units are unable to supply all the loads, MG energy management can voluntarily curtail the non-sensitive and non-critical loads utilizing adaptive strategies, ensuring that the sensitive and critical loads are not interrupted. However, for real-time MG energy management may be difficult to determine optimal operating points of generation and energy storage to minimize non-critical energy uses to provide longer emergency supply to critical loads. Our analysis focuses on critical MG components to improve the supply availability in extreme events, through the optimized use of DER units and load prioritization. The application of the defensive and optimized MG islanding is determined by a risk assessment, component weather-dependent failure probabilities and fragility curves to identify the most vulnerable ones. The islanding operation mode can occur if there is a fault within the upstream network to which the microgrid is connected or by choice. In islanded operation, the supply to the loads within the MG depends upon the generated power of the DG units, energy storage reserves and through the energy management to curtail non-critical loads, based on specific load prioritization algorithms [8-23].

The analysis focuses on critical MG components to improve the supply availability in the case of extreme events, through the optimized use of DER units [12-18]. The application of the defensive and optimized islanding solution is determined by a risk assessment, specifically, by the component weather-dependent failure probabilities by using existing unit fragility curves to identify the most vulnerable components, at higher risk of tripping due to the event. Risk assessment enables informed decisions regarding actions to mitigate risk. The defensive islanding algorithm is based on constrained clustering, using power flow analysis to split the system into islands and isolate the vulnerable components [18- 24]. The islanding operation mode can occur if there is a fault within the microgrid or in the upstream network to which the microgrid is connected. In islanded operation mode, the energy supply to loads within the MG depends upon the generated power of the microgrid DG units, ESS reserves and through the energy management (system) functions to curtail the non-sensitive and/ or non-critical loads, based on a load prioritization algorithm [1-8,18-24]. Large-scale embedding of microgrids into power systems offers values for resilience and service restoration. The deployment of the microgrid at extended scale has the potential to revolutionize grid resilience, flexibility, and sustainability, through the microgrids’ advanced and intelligent energy management schemes and adaptive islanding. Other benefits of the microgrid research include: a more reliable electric service for microgrid residents, the existence of local service helping communities to cope with wide-area grid outages, and reduced risks of cascading failure, facilitating the service recovery. By dynamically managing local energy generation and resources the microgrids can optimize efficiency, minimize the cost, or maintain stability.

Optimized and simplified MG component models are critical in developing and implementing MG generation scheduling and power models [14-24]. The power generated by one panel P1pv is calculated according to

The wind generator power output is best estimated through interpolation of the values of the data provided by the manufacturers with wind velocity observations. As the power curves are quite smooth, they can be approximated using a cubic spline interpolation. Several forms of an ESS are available in practice, such as supercapacitors, electrochemical batteries, super-conducting magnetic energy storage, compressed air energy storage and flywheel energy storage. Electrochemical batteries were selected in this study due to their popularity in storing electrical energy. The storage system can minimize the effects of the stochastic nature of RESs on microgrid to balance power generation and demand. The charging and discharging models of the battery can be represented as follows:

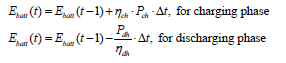
These are subject to the following battery power and energy limits constraints:

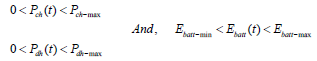
where P_ch(t) and P_dh(t) are the charging and discharging powers of the battery at time, t, respectively, E_batt(t) is the storage energy, η_ch and η_dh are the charging and discharging efficiency, respectively. The operating commands, u(t), of the battery from the optimization scheduling algorithm determine the charging and discharging energy amount. The positive values of u(t) indicate P_ch(t) while negative values refer to P_dh(t).

Interruptible loads are disconnected during an outage. The realization of interruptible loads will help to save energy and to use power in a meaningful way, when sizing the local power generation capabilities. Examples of interruptible loads in the household are the loads in the kitchen, entertainment, washing machine, air conditioning, or EV charging. Typical load profiles are determined by using recorded data. To optimize the loads in an efficient manner, we are dividing into three different categories as: a) inflexible loads, sub-divided into: most critical loads, critical loads, and essential loads; and b) flexible loads, sub-divided into: transferable, and non-critical loads [1-8,19-24]. The essential loads are the first to be shed followed by the critical in the event of contingencies, while the most critical loads should be maintained except otherwise, wherein the system is on the verge of collapsing. For all loads, we assume that the demand is bounded by:

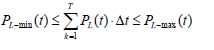
The core of the MG energy management system, in the case of the extreme events, and grind interruptions is to provide power to essential and critical loads, though power management and allocation, and through the load optimization and prioritization. The low voltage grid has mostly a simple, radial topology. The full knowledge of the cable characteristics and lengths would allow a power flow calculation and imposing current and voltage limitations during the optimization. However, there is a practical drawback to this approach: the topology at the LV level is not always available. To overcome this problem, the model uses simple power limits at the feeders and the secondary substation. The import and export power at time t is denoted as Pgrd(t) in kW, with the following interpretation:

For reliably grid operation, the power that is exchanged, must be within the following limits:

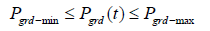
where P_grd-min and P_grd-max are the grid minimum and the maximum power exchange limits. The fuel cost of diesel generators, natural gas generators or microturbines is expressed as a quadratic function of its active power as:

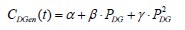
where α, β, and γ are the generator coefficients which can be obtained from the manufacturer. The DG output power should satisfy the power and ramp rate constraints at each time-period. In practice a diesel generator operation in the range of 70% to 90% of full load is preferred for economic considerations and recommended by manufacturer. Diesel generators are helpful in boosting power during peak energy demand hours as well as for energizing the energy storage units as and when required. Power limits for diesel generators can be expressed as:

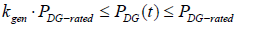
The value of k_gen is set to 0.25 to 0.35 based on the manufacturers’ recommendations. Generation scheduling and power flow are formulated as a mixed-integer linear program, and then reformulated as a twolevel problem. The first level identifies for each component, the optimal operation and scheduling, while in the second level models the system operations under the worst-case scenarios. Since the optimal scheduling of a MG is a fundamental prerequisite for emphasizing the MG merits, a resiliency-oriented linear programming approach was adopted. The main features of the proposed approach are listed here: develop a two-stage optimization model with real-time network constraints, then an efficient framework for modeling MGs, employing MG simplified components and demand response for mitigating the impact of high-impact, low-probability events. This model exploits optimal energy uses and load prioritization. In islanded operation the optimum power balance is more critical than in grid-connected operation mode. Therefore, reliable energy sources and storage are crucial elements to improve a microgrid operation (). The rigorous models of the microgrid’s generation and energy storage resources, and options, along with prevailing uncertainties are key factors in achieving the desired MG operations in the case of extreme events. MG uncertainties are categorized into: normal operation and contingency-based uncertainties. Therefore, random parameters are represented in the MG scheduling along with their associated probabilities. The proposed operation and power management approaches are flexible and can be extended and applied to any MG configurations and types. The framework minimizes the cost function of MG, taking into account the operational constraints. Since the resiliency-oriented MG scheduling models are computationally intensive, the scenarios associated with the uncertain parameters were sensibly reduced for computational tractability. The cost function (TF) which is minimized in order to obtain the minimum MG cost, is expressed by:

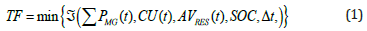
Here, the terms P_MG are the maximum available values of the active power that can be generated in the microgrid by the nondispatchable and dispatchable units, and the available energy of the storage devices. The terms CU(t) are the usage coefficients in relation to the maximum values of the active powers (rated power for generators and maximum capacity for energy storage), in their variation domain [0, 1]. AV_RES(t) represents the availability function of RES units, given by input data, e.g. the solar irradiance level or wind availability, by using the weather forecasts or prediction models. The loads are specified based on load profiles for critical, essential, non-critical, priority or transferable types. Load profiles are modeled by using probabilistic and stochastic models [18,16-24]. Decision variables include generated power by each MG source and stored energy, computed by multiplying its estimated usage coefficient with the rated power at each time step. The optimization energy management and optimal generation scheduling are constrained by the generation and stored energy to meet the specified loads, by solving the MG energy balance equations with specified constraints. The minimization procedures are applied at each time step, over specific time intervals. The inputs are weather forecasts or prediction models, load profiles (load coefficient, and reserve estimates, and represented as a black box of the minimization process (Figure 1). The MG energy and power balance equations are based on load forecast or profile, wind velocity and solar radiation data or forecast, energy storage data, dispatchable and distributed generation units, expressed as:

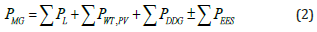
Here, P_MG is the microgrid power balance (usually zero in the islanded operation), P_L is the total load power, P_WT,PV, P_DDG, and P_EES are the wind turbine and/or P_V, dispatchable DG power, and from the ESS units. The energy balance equation is obtained, by integrating of power equation, over a specific time interval, with the term significance as before:

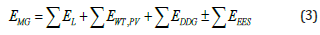
Results and Discussion

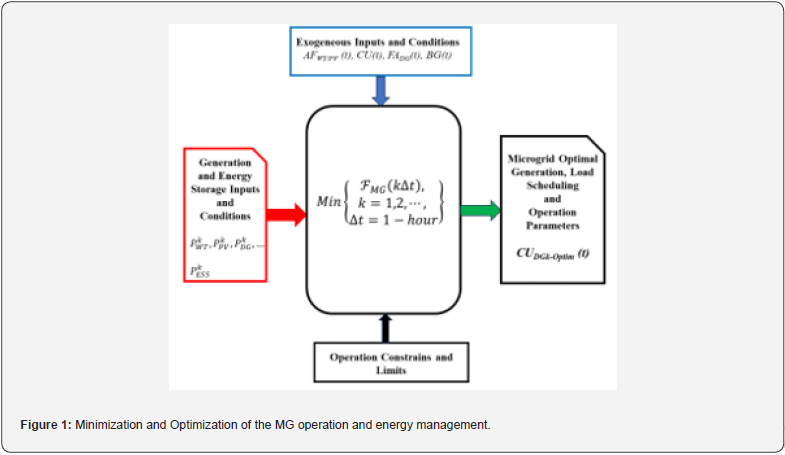
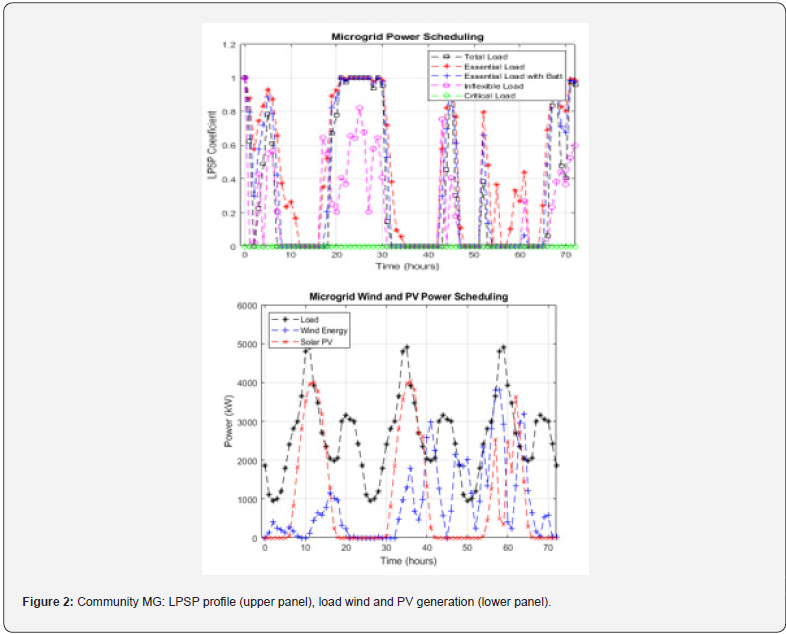
The proposed optimized energy management and optimal generation scheduling algorithms were calibrated on various MG configurations, unit sizes and for different time intervals, and load profiles and demands. The dynamic composite load models [1-9,19-24] are used in our approaches to extend the supply duration. Figure 2 shows results for a small community microgrid with wind and solar energy units. It consists of a 5 MW maximum load demand, 3 MW installed wind power, 4 MW rated PV power, and 2 MW dispatchable distributed generation. The actual wind velocity and solar radiation data are used. The loss of power supply probability (LPSP), the loss of power supply (LPS) to total demand for a considered period LPSP for various load types and profiles are shown in the upper panel. The graphs show that the power for critical loads is continuously supplied. Load prioritization and adjusting the load demand can significantly improve the MG resilience, extending energy supply for essential, critical, and most critical loads. The proposed methods calculate the optimal generation scheduling of the distributed non-dispatchable and dispatchable generators and energy storage as per load demand, taking in account power unit constraints, load prioritization and reserve availability at each time step. Figure 3 shows the same results, but for a smaller residential or commercial facility microgrid, and for various combinations of loads and generation levels of the RES and DG units. It is important to emphasize the load prioritization and adjusting the load demand can significantly improve the resilience of the microgrid, by extending energy supply for critical and most cortical loads. The generation scheduling is based on the power management strategies discussed above.

The optimal generation scheduling and power balance methods were tested and validated on several MG configurations, load profiles, dispatchable and RES generation units and scenarios, to verify the proposed models and algorithms. The generation scheduling is based on the power management strategies discussed above. The optimal generation scheduling and power balance methods were tested on several MG configurations, various load profiles, dispatchable and RES generation scenarios. Besides the testing the optimal scheduling and energy management system algorithms for various MG configurations, using predicted and real wind and solar radiation data, load profiles and fuel reserve scenarios, additional tests of the proposed scheduling models and load prioritization were conducted using PowerWorld and RTDS simulators.

In the case of extreme events, the energy management system finds an appropriate and optimal MG energy schedule, considering available power generation resources, load demand, load prioritization algorithm, and energy storage status. The scheduling models ensure the optimal MG operation, reducing vulnerability and providing extended power supply at least for critical and essential loads. Implemented and validated MG optimal generation scheduling, power management, and load prioritization show that it is possible to provide an un-interrupted energy supply for critical and essential loads in the case of extreme events. Embedding microgrids into power systems offers value for resilience and service restoration.

The MG deployment at extended scale has the potential to revolutionize grid resilience, flexibility, and sustainability, through the MG advanced and intelligent energy management schemes and adaptive islanding. Other MG benefits include: a more reliable electric and improved quality service for microgrid residents, local service helping communities to cope with widearea grid outages, reduced risks of cascading failure, facilitating the service recovery or even lower energy costs. By dynamically managing local energy generation, energy storage and resources, a microgrid can optimize efficiency, minimize the cost, or maintain system stability.

We developed improved power and energy MG models with limited generation resources to serve critical loads in the case of an extreme event. These models include the DG uncertainties, MG simplified component models, load prioritization, load composite dynamic models, and power management algorithms. MGassisted critical load service restauration problem is formulated as constrained programs. Models include maximizing the energy provided to the critical and essential loads weighted by their priority index and minimizing the overall MG energy use. Effects of loads prioritization are studied and evaluated for various MG configurations. Our results indicate that reliability is improved, and the service is continuously provided to the critical and essential loads in cases when load prioritization algorithms are employed, compared with cases when no load prioritization is used.