F. Zama*

doi:10.19080/ARR.2018.04.555656

Review Article

Iteratively Reweighted Least Squares Algorithm for Nonlinear Distributed Parameter Estimation

F. Zama*

Department of Mathematics, University of Bologna, Italy

Submission:August 09, 2019;Published:August 26, 2019

*Corresponding author: F. Zama, Department of Mathematics, University of Bologna, Piazza Porta S. Donato, 5 40127, Bologna, Italy

How to cite this article:F Zama. Iteratively Reweighted Least Squares Algorithm for Nonlinear Distributed Parameter Estimation. Ann Rev Resear. 2019; 5(2): 555656. DOI: 10.19080/ARR.2019.05.555656. DOI: 10.19080/ARR.2019.04.555656

Abstract

The distributed parameter estimation problem is solved in the case of non-smooth parameters. The extension of the Iteratively Reweighting Least Squares algorithm (IRLS) is formulated for the nonlinear problem. A sequence of weighted least squares problems is solved by a Trust Region Levemberg Marquardt method with automatic update of the regularization parameter. The algorithm, named NL-LM-IRLS, is presented as an extension of IRLS applied to the minimization of a nonlinear problem. The results on some preliminary tests are reported in the numerical experiments and confirm the validity of this approach.

Keywords: Iterative gauss newton, Trust region levemberg marquardt, Non linear minimization, Numerical experiments, Least squares problems, Regularization parameter, Linear problems, Convex problem, IRLS, Preliminary results, Mapping, Algorithm, Substitutes, Residual vector, Diagonal matrix, Machine precision, Inverse problem, Jacobian matrix, Computed regularization parameter, Armijio backtracking procedure, Embedding, Tolerance parameter

Introduction

In the treatment of distributed parameters estimation, the usual choice is that of minimizing the error norm using the least squares distance. This paper considers the problem of estimating distributed parameters representing properties of material that change over the spatial domain. In this case the parameters are represented by non-smooth functions. Moreover, the data may be affected by noise containing outliers that cannot be easily removed. In all these cases a great improvement in the solution can be obtained by solving a minimization problem in the $p$ norm where 0p<<∞. When the norm $p=2$ is used, then the regularized nonlinear least squares problem can be efficiently solved by the Iterative Gauss Newton (IRGN) method as reported in [1,2] and references therein. The case 1p<<∞is efficiently treated by the Iterative Reweighted Algorithm IRLS proposed in [3] for linear problems. We propose here a direct extension of such algorithm to the solution of non linear problems where 0p<<∞. The non linear least squares and possibly non convex problem is substituted by a sequence of weighted least squares approximations which efficiently solve the non linear identification problem. The algorithm, named NL-LM-IRLS, is presented as an extension of the IRLS applied to the non linear minimization problem. Some preliminary results on one dimension identification problems are reported confirming the validity of this approach. In section 2 we explain the details of the iterative method and report the numerical experiments in section 3.

Methods

Method We consider the discrete finite dimensional problem of estimating the parameter q∈R^kof a differential model (state equation) c(u, q) = 0, usually an ordinary or partial differential equation. We assume that the measurements are obtained by mapping the solution of the state equation u(q) (state variable) at some measurement points y=F(u(q)). The parameter identification is obtained by minimizing a cost function J(q) representing the data fit term. In our work we define:J(q)≡||F(q)-y||_phence the parameters are obtained by solving the following minimization problem:

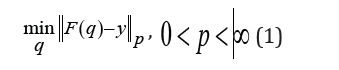
In the case 1 < p the Iterative Reweighted Least Square method (IRLS) is widely applied in the context of linear models and recent developments are given for example in [4-6].

We propose here an extension of the IRLS algorithm for the minimization of non linear models in the l_p norm with 0 < p < ∞ .

The IRLS method substitutes the problem (1) by a sequence of weighted least squares problems:

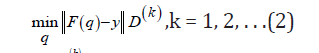
where the weights D^{(k )} are diagonal matrices obtained by the residual vector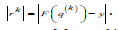.Assuming that 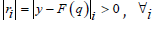, we observe that problem (1) can be restated in the following equivalent form:

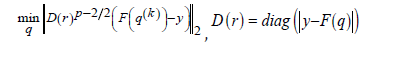
Since the residual r^k , computed at each step k, depends on the approximate solution q^k , the diagonal matrix D^kis modified to manage the possible pres- ence of zero elements in r^k [7]:

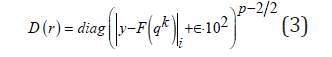
where s represents the machine precision. The Non Linear Iteratively Reweighted Algorithm (NL-IRLS) is reported in Algorithm 1. The algorithm requires the solution of a sequence of weighted nonlinear least squares problems which suffer from the ill conditioning of the inverse problem. In our approach we apply the Levemberg Marquardt (LM) method [8,9] which consists in the following minimization.

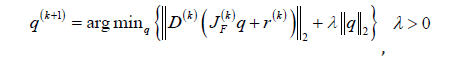
where 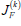is the Jacobian matrix relative to F in the iterate q^(k) and λ > 0 is a suitably computed regularization parameter. In our implementation the LM method is obtained by computing a sequence of approximate solutions 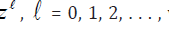where and computing a vector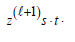

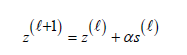
where s^(l) solves the linear system:

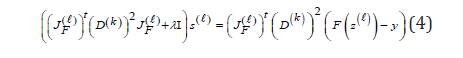
and 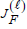is the Jacobian matrix relative to F in the iterate 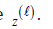. The step size α > 0 is obtained by means of an Armijio backtracking procedure to guarantee the decrease of the weighted residual norm.

The whole algorithm is defined as follows:

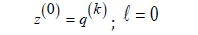
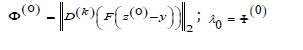
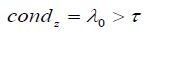
while cond_z

α =1

Compute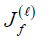

Compute s^(l) by solving (4)

while cond_α

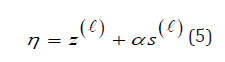
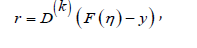
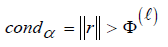
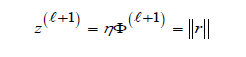
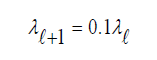
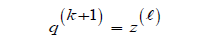
Embedding (5) in the IRLS algorithm reported in Algorithm 1 we obtain the Nonlinear Regularized IRLS algorithm (NL-TR-IRLS) reported in Algorithm 2. The exit test is based on the relative distance between the iterates q^k+1 , q^k . The same tolerance parameter τ =10⁻⁶  is used both in (5) and NL-LM-IRLS algorithm (Algorithm 2).

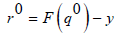
repeat

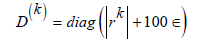
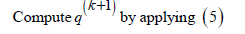
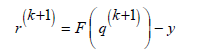
until exit test

Algorithm 2: Nonlinear Levemberg Marquardt IRLS Algorithm (NL-LMIRLS).

Numerical Results

In this section we discuss the application of the NL-LM-IRLS method to parameter identification problems. In these problems the parameters are often close to piecewise constant or linear functions. We consider the problem of identifi- cation of the reaction coefficients in elliptic problems in one spatial dimension. The experiments are carried out on Intel Core i7 using Matlab R2018a. The test problem concerns the identification of the reaction parameter q(x) in the stationary model:

the function f is defined by setting

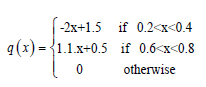
and the parameter q (x) is defined as follows:

The discrete reference solution of the state equation (6) is computed by linear finite elements, sampling the spatial domain with a uniform grid of M = 90 points

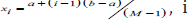
i= 1, . . . , M . The measurements y are obtained by interpolating

the reference solution in the measurement points defined by a uniformly spaced grid of N = 55 points: a = ξ1 < ξ2 <...ξ N−1 < ξ N = b . The coefficients of the computed parameter qreg are compared to the true parameter qtrue by means of the Parameter Relative Error

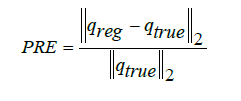
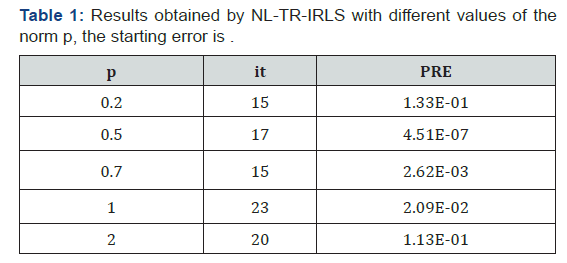
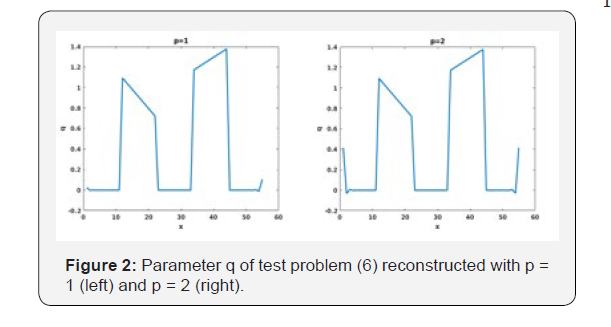
This experiment aims to investigate the approximation results obtained by the NL-TR-IRLS algorithm when the parameters are non smooth functions. For this reason we compare the different reconstructions using the 0 < p ≤ 2 norms. From the data reported in Table 1 we observe that the best reconstruction is obtained with p = 0.5. The plots reported in Figures 1 & 2 show the different reconstructions of the parameter q. We can observe a very noisy solution when p = 0.2 (Figure 1) and large oscillations at the boundaries when p>0.5 (Figure 2) the parameter q is perfectly reconstructed when p = 0.5 (Figure 1).]

Conclusion

The distributed parameter estimation problem has been solved in case of non smooth parameters. The extension of the iterative least squares method to non linear parameter identification (NLLM- IRLS) proves to be very promising. Future work includes the introduction of an automatic parameter computation such as in [10-12]. Further tests will be carried out on noisy and higher dimensions problems.

......................