Review article

Quantum Mechanics as a Fourier Representation of a Relativistic Quantum Particle

Eliade Stefanescu*

Advanced Studies in Physics Centre of the Romanian Academy, Romania

Submission: September 09, 2018;Published: December 17, 2018

*Corresponding author: Eliade Stefanescu, Advanced Studies in Physics Centre of the Romanian Academy, Academy of Romanian Scientists, Bucharest, Romania

How to cite this article: Eliade Stefanescu. Quantum Mechanics as a Fourier Representation of a Relativistic Quantum Particle . Ann Rev Resear. 2018; 4(4): 555641. DOI: 10.19080/ARR.2018.04.555641

Abstract

The starting point of this research is a representation of a quantum particle according to the Schrodinger equation of the conventional quantum mechanics. In this representation, a quantum particle is described by a wave packet in the coordinate space and the conjugated wave packet in the momentum space. The problem is that while in the coordinate space the group velocity is in agreement with one of the Hamilton equations, the group velocity in the momentum space is in contradiction with the other Hamilton equation - a minus sign is missing. Group velocities in agreement with the Hamilton equations are obtained only when in the time dependent phase of a quantum particle wave packet, instead of the Hamiltonian coming from the conventional Schrodinger equation, the Lagrangian is considered. This suggests us to consider the relativistic Lagrangian in the time dependent phase. In this way, the conventional relativistic principle of invariance of the time-space interval gets the more physically understandable form of the invariance of the time dependent phase of a quantum particle - the time dependent phase of a quantum particle is the same in any system of coordinates. Based on the relativistic time dependent phase invariance of a quantum particle, from the group velocities of this particle the relativistic kinematics and dynamics are obtained. The interaction with an electromagnetic field is described by a modification of the time dependent phase with a scalar potential conjugated to time and a vector potential conjugated to the space coordinates. In this paper, we find that, according to the formalism of the general relativity, any matter element in a field of forces is accelerated only perpendicularly to its velocity. This means that the matter propagation of a quantum particle can be conceived in planes perpendicular to velocity, while the mater distribution can be considered in a Fourier representation - quantum waves. We study the quantum particle dynamics in gravitational waves and derive the graviton spin. We consider a quantum particle in electromagnetic field and obtain a Schrödinger-Dirac-type equation, with additional terms describing the velocity dependence of the particle dynamics.

Keywords: Quantum particle, Wave packet, Group velocity, Lagrangian, Hamiltonian, Maxwell equations, Spin, Metric tensor, Covariant derivation, Gravitational wave, Graviton spin, Hamilton equations, Conjugated, Schrödinger equation, Amplitude, Curvilinear coordinates and Christoffel symbol

Introduction

We live in a period when the fundamentals of physics are put under discussion [1-9]. For instance, in the framework of open quantum physics [10-14], we found that the general principle 2 of thermodynamics, of the entropy increase, was in fact not so general, but only for molecular systems. In the more general case of a system including a coherent electromagnetic field, the entropy could also decrease [12]. On this basis, an interesting phenomenon of environmental heat conversion into usable energy has been discovered [11-18]. Some time ago, we also discovered that the conventional Schrödinger equation is contradictory to the Hamilton equations [19], which are fundamental for the matter dynamics. Really, the dynamics of a particle is perceived in a three-dimensional space of coordinates defined by a position vector , 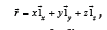and in time, defined by a scalar t. For a matter object we define an inertial property called mass,, and a dynamic quantity as the product of the mass with the velocity 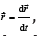, called momentum,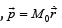. The dynamic law of a particle can be defined as a conservative process, by a conservative quantity, called energy,

as a sum of the kinetic energy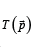, which depends on momentum, and the potential energy 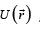, which depends on the coordinates. From the conservation condition

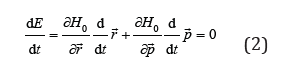
we obtain the dynamic equations called Hamilton equations,

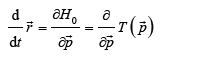
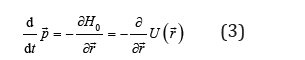
depending on the potential energy gradient called force, while the energy as a function of coordinates and momentum,

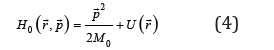
is called Hamiltonian. However, this classical description tells us nothing about the structure of the physical world. Only Quantum Mechanics tells us something about the structure of this world. Namely, that this world is composed of species of identical quantum particles. On one hand, experimentally, it has been found that these particles are of a wavy nature. On the other hand, one could find that the simplest way to define a quantum particle is by a wave packet, with the momentum conjugated to the coordinates, and the energy conjugated to time, with a single quantum constant h [20-22]:

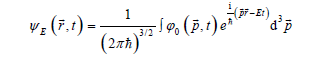
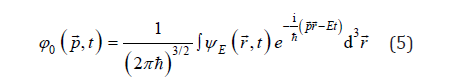
In this case, one can define a momentum operator

and a Hamiltonian operator,

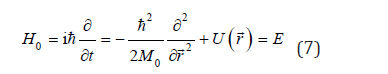
With these operators one obtains eigenvalue equations, for momentum,

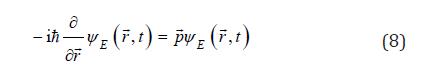
and for energy, as a Schrödinger equation:

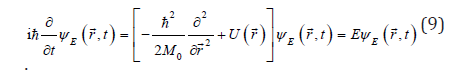
However, when the group velocities are calculated for the wave packets (5), which with (1) are of the form

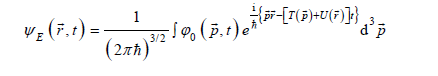
we obtain an erroneous equation, contradictory to the corresponding Hamilton equation:

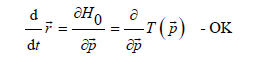
We get back the minus sign only if instead the Hamiltonian

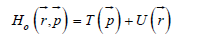
we consider the Lagrangian

In his case, the wave packets (10) take a form

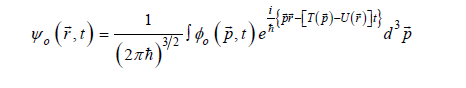
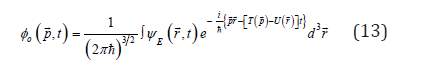
with group velocities in agreement with the Hamilton equations (3):

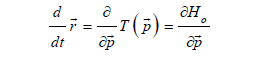
However, this description is still unrealistic, having an infinite spectrum of waves, as a function of the velocity r . A finite spectrum is obtained when the relativistic Lagrangian

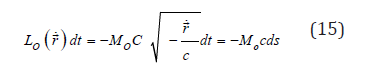
is considered in the time dependent phase of a particle wave [13, 19-22]:

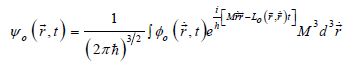
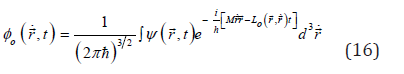
From these expressions with (15), we noticed that the invariance of the time-space interval of the Theory of Relativity is equivalent to the invariance of the time dependent phase of a quantum particle. We defined a Relativistic Quantum Principle of invariance of the time-dependent phase [23-27]. On this basis, we obtained the relativistic transform of the space-time coordinates, and the relativistic dynamics for the particle waves. We considered a quantum particle in a field described by a vector potential conjugated to coordinates, which is in agreement with the theory of Aharonov and Bohm [28], and a scalar potential conjugated to time. We obtained the Lagrange equation as a group velocity of the particle waves, the Lorentz force, the Maxwell equations, the relativistic transform of the electromagnetic field, and the spinstatistic relation [13, 19, 23-27].

In this paper, we adopt the converse starting point, not of the quantum mechanics, but of the general theory of relativity, where a quantum particle is a piece of matter with a density normalized to mass. In section 2, we find that, according to the general theory of relativity, this matter propagates in planes perpendicular to the velocity, which means that the matter propagation can be considered in a Fourier representation, as a group of waves. In section 3, we find a relativistic invariant of the matter density, and derive the equation of the matter conservation. In section 4, we find a dynamic equation of the velocity field as a function of the metric tensor. In section 5, we obtain the particle oscillation in a gravitational wave. In section 6, we find the particle acceleration in a gravitational wave, and define a gravitational invariant including a proper dynamic, called spin. In section 7 we consider the graviton spin as a matter rotation and find the angular momentum St=2. In section 8, we obtain a pseudo-energy tensor proportional to the square of the gravitational amplitude. In section 9, we obtain a fully relativistic dynamic equation. In section 10 we give a summary.

Quantum Particle as a Distribution of Matter

We consider a quantum particle as a distribution of matter with the density as a positively defined quantity:

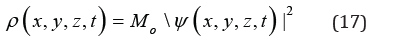
satisfying a normalization condition

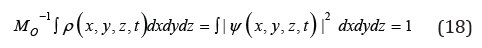
According to the general theory of relativity [29, 30] in a system of curvilinear coordinates

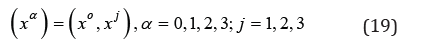
we define a velocity field in the system of the proper time

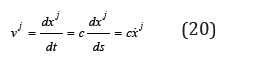
We define the differential time-space interval ds , which depends on the metric tensor g_uv

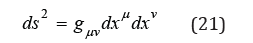
From this expression, we obtain the fundamental property of the velocity field

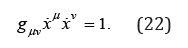
Since the covariant derivative of the metric tensor is null, this property takes the form

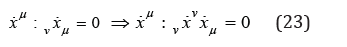
which means that any covariant variation of a velocity, or any covariant acceleration, is perpendicular to this velocity. At the same time, for any quasi free particle, i.e. when no external force is present, any matter element follows a geodesic trajectory,

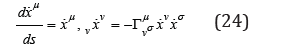
which means that the covariant acceleration is null:

In this case the acceleration , v v x x μ   of any differential element of matter includes only a component induced by the gravitational field described by the second kind Christoffel symbol

When an external force is present, an additional, external acceleration Aμ arise,

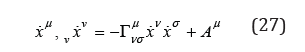
This acceleration is of the form

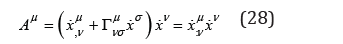
which means that any acceleration induced by an external field is a covariant acceleration, while the acceleration induced by an internal, gravitational field, does not modify the covariant

acceleration. It is interesting that by multiplying the external acceleration (11) with the velocity xμ , and taking into account the fundamental property (7),

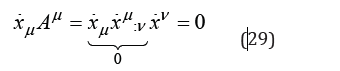
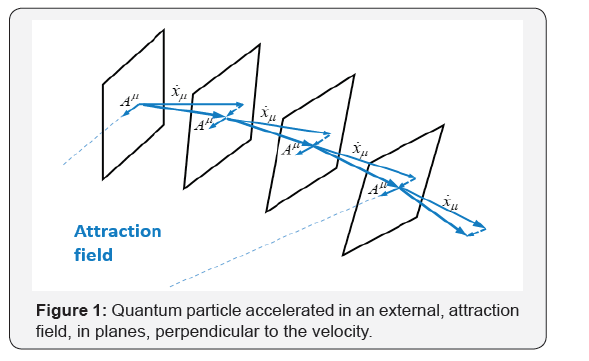
we find that any external acceleration is perpendicular to the particle velocity. This means that a particle can be conceived as a distribution of matter moving in planes perpendicular to the velocity (Figure 1) the external forces acting on the particle modifies the matter distribution in these planes, but not in between these planes (Figure 2).

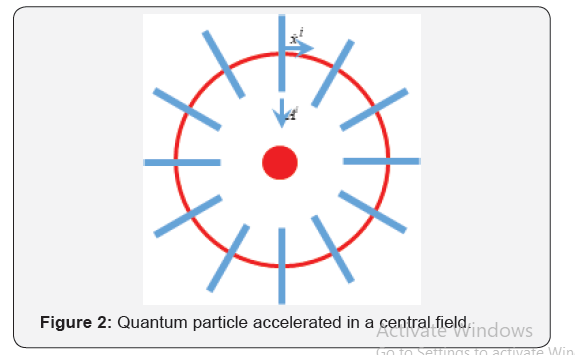
Thus, according to the general theory of relativity, the distribution of matter in a central field takes the form of an atom. This means that the distribution of matter of a quantum particle in a system of curvilinear coordinates can be considered in a Fourier representation,

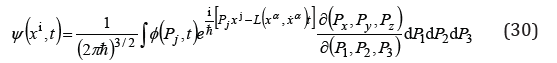
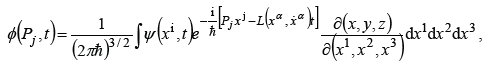
with the normalization condition (18),

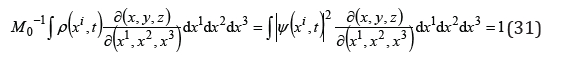
for the matter density

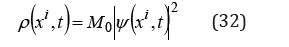
and the Lagrangian

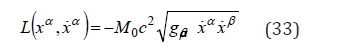
while t is the proper time. In a stationary state, gαβ ,0 = 0, gi0 = 0 , with the general property (6), the momentum is

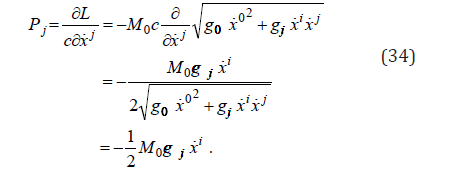
With these expressions, from the group velocity in the coordinate space, we find an equation, which with (6) takes the form an identity,

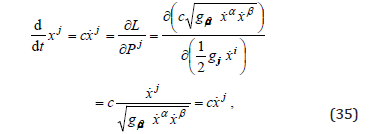
while from the group velocity in the momentum space, we find the Lagrange equation,

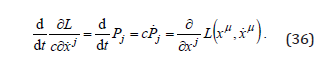
For the Hamiltonian

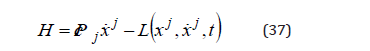
from its differential with the Lagrange equation,

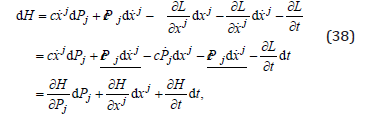
we obtain the Hamilton equations

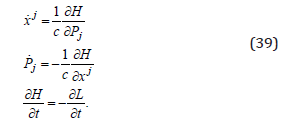
In this way, the dynamics of a quantum particle as a distribution of matter, of density (17) and the normalization condition (18), or of the wave functions (30) with the normalization conditions (31), is described by the dynamics of the matter differential elements according to the Hamilton equations (39).

The Matter Conservation

We consider the density normalization in two systems of coordinates,

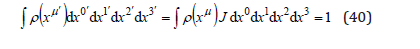
which depends on the Jacobian

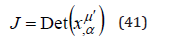
It is interesting that this Jacobian has the same elements as the tensor transformation. From the transform of the metric tensor between these two systems of coordinates,

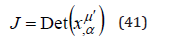
with the determinant

we obtain the Jacobian

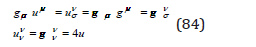
With the volume differential elements

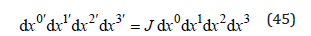
the density integral on an arbitrary volume V takes the form

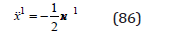
which means an invariance relation of the matter density, depending on the quantity 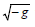we call scalar density,

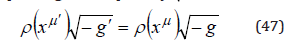
We define the matter flow four-vector

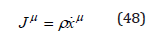
with the conservation relation

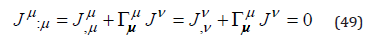
With the second kind Christoffel symbol

and the symmetry of the metric tensor, the coefficient of the last term of equation (49) is

In this way, the conservation relation (49) of the null covariant divergence of the matter flow four-vector takes the form of a null ordinary divergence,

By integrating in a space volume,

and separating the time term from the space terms, we obtain the conservation relation under the more understandable form of the time variation of the matter contained in a volume V , due to a flow 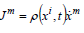through the surface of this volume,

For a low velocity, 0 x = 1 , weak gravitational field, g = −1 , we obtain the ordinary conservation relation:

Dynamic Equation of a Quantum Particle as a Distribution of Matter

As we showed in the previous sections, a quantum particle in a system of curvilinear coordinates can be considered as a distribution of matter with the positively defined density (32), as a function of the Fourier expansions (30), with the Lagrangian (33), and the canonical momentum (34). The matter density satisfies the matter conservation relation (55), which is

and the invariance condition (47), which is

From the second equation (30) with the fundamental property (21), the group velocity in the momentum space is

while from the derivative of (34) we obtain

We notice that the second derivative of the coordinate in this equation can be eliminated with the geodesic equation

From (58)- (60), we obtain,

With the expression (50) of the second kind Christoffel symbol, we obtain the dynamic equation

for the differential elements of the matter of a quantum particle.

Quantum Particle Oscillation in a Gravitational Wave

A gravitational wave is a solution of the second order wave equation

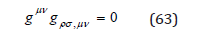
We consider such a solution of the form

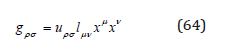
where uρσ is called amplitude tensor, while lμν is called polarization tensor. With this solution, from the wave equation (63) we obtain a normalization condition for the polarization

tensor

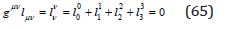
We notice that the metric tensor, being symmetric, it can be diagonalized. By a space-time diagonalization, g _j0 = 0 the dynamic equation (62) takes the form

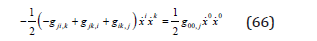
this equation takes the form

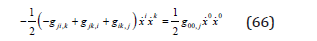
With the Christoffel symbol of the first kind,

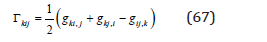
this equation takes the form

Since the gravitational waves are created by motions of large masses, we consider small velocities, x0 =1 , which means that the dynamic equation (68) takes the simpler form

By multiplying this equation with x j , and taking the first kind Christoffel symbol as a function of the Christoffel symbol of the second kind,

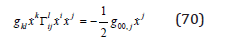
with the geodesic equation (60), we obtain a dynamic equation for the acceleration of a matter differential element in a gravitational potential g0

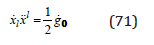
By taking into account the derivative of the gravitational potential with the proper time,

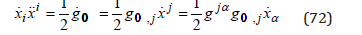
and a space-time diagonalization of the metric tensor, g ^jα = 0 , we obtain the dynamic equation

which is

It is interesting that the first order derivatives of the gravitational potential (64) which is of the second order in the spatial coordinate, are of the first order in these coordinates. We obtain the dynamic equation

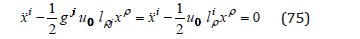
which with the condition

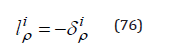
takes the form of a harmonic oscillation

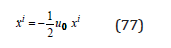
Let us consider a wave oscillating in the direction 1 x , corresponding to a polarization tensor

which satisfies the condition (65). With a metric tensor for a weak gravitational field,

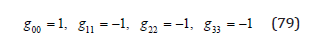
the polarization tensor is

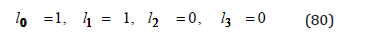
For a system with rotational symmetry, while the amplitude tensor is of the form

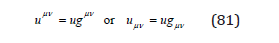
and a low velocity, while the fundamental property (21) is

we obtain

From

we obtain the coefficient

we call gravitational wave amplitude. With this expression, the dynamic equation is

which describes a harmonic oscillator with the frequency

Quantum Particle Acceleration in a Gravitational Wave and Proper Dynamics

In the previous section, we showed that a gravitational wave described by the wave equation (63), with a second-order solution (64), means an oscillation of any matter differential element with the frequency of this wave. However, we notice that the wave equation (63) accepts also a first-order solution,

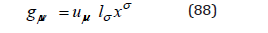
with a normalization condition similar to

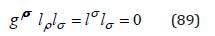
With this solution, from (74) we obtain the dynamic equation

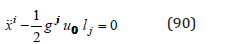
which, with (5.20) is

We notice that a solution of the form (88) means a constant acceleration of any differential element of matter in the direction of polarization of the gravitational wave. No oscillation is perceived by such an element in a gravitational wave. With the expression (81)

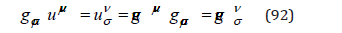
by multiplying with l_ν , we find an equation for amplitude tensor:

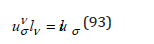
We consider a gravitational wave polarized in the direction x³ ,

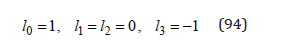
and a weak gravitational field, with the metric tensor elements

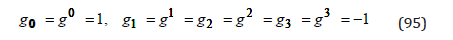
With (93), from (92) we obtain the equations

which, with (95) become

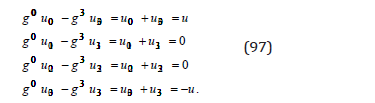
From the first and the fourth equation (95) we obtain

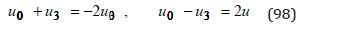
From the second equation (98) with (84)

we obtain

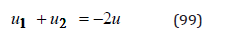
With the contravariant elements of the polarization tensor/p>

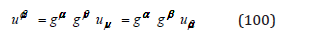
we calculate the gravitational invariant

The Graviton Spin

As we have shown in the preceding sections, a gravitational wave is described by an amplitude tensor u_μν We define the operator R ^δα of rotation with a differential angle δα in a plane (x, y). For a vector

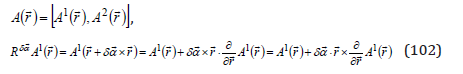
With the angular momentum operator

the rotation operator (109) takes the form

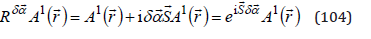
This means that the operator of rotation with an arbitrary angle α  is

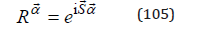
We notice that a rotation with an angle is equivalent to an inversion,

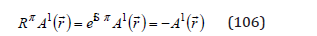
This means that a vector A(r) describes a rotation with the spin S =1 . For a rotation with an

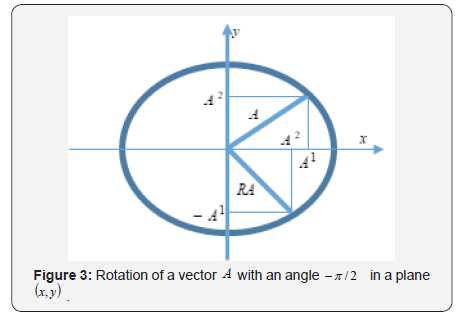
Angle −π / 2 , as it is shown in (Figure 3), we obtain

Now, let us consider a rotation with an angle α  in the plane(x, y) of a tensor uμν (x, y) . From the invariance of an arbitrary scalar of the form

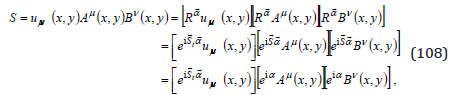
we deduce the spin eigenvalue of a tensor S_t=-2 , i.e. a spin |S|_t = 2 . For a rotation with an angle −π / 2 ,

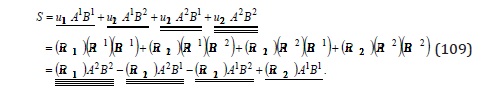
We obtain

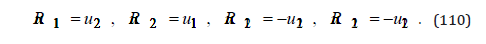
Let us consider the vectors

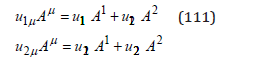
By rotating this vector with an angle −π / 2 ,

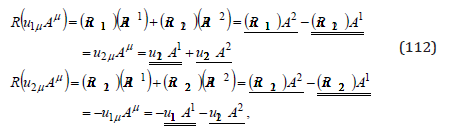
we obtain again

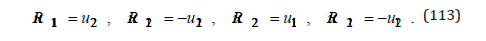
Let us consider a rotation of the scalar (114) with an angle −π / 4 :

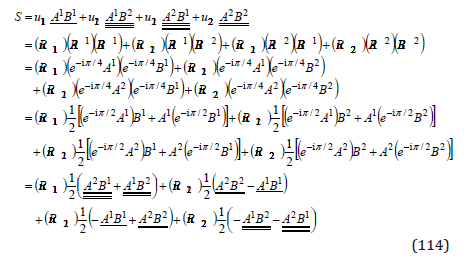
We obtain the relations:

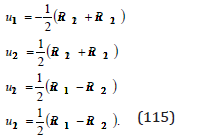
With the relations

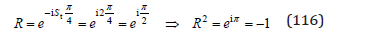
equations (7.21) become:

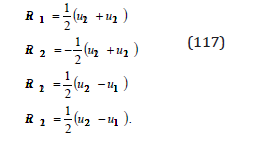
By rotations R , the two terms of the gravitational invariant (104) are transformed one another:

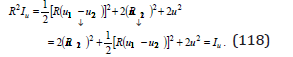
This means that this invariant includes two components: a component u , which means a matter acceleration according to the expression (91), and an oscillating component u₁₁ ,u₁₂ = u²¹ ,u2 , describing an oscillatory motion - the spin.

Gravitational Action and Pseudo-Energy Tensor

We consider the gravitational action as an integral of the total curvature of the space,

where we used the notation . With the Ricci tensor (Appendix A),

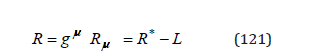
the total curvature is of the form (Appendix B)

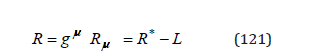
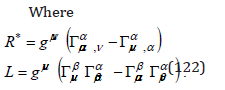
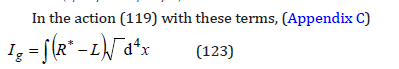
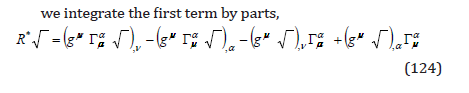
and, since the variations of the action at the integration limits are null by its definition, we eliminate the total derivatives. In this case, we can take

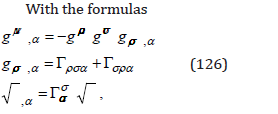
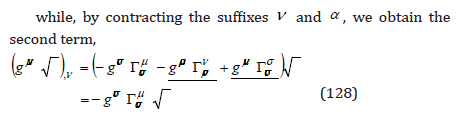
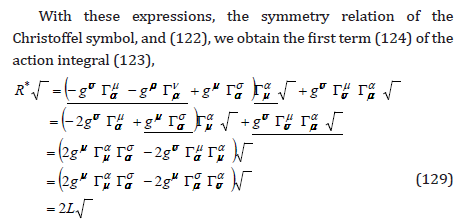
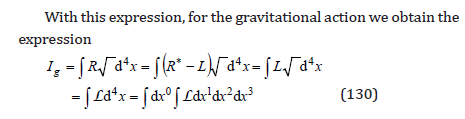
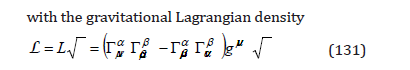
which depends on the variables g^μν which here we consider as “coordinates” and the variables g_μν ,σ considered as “velocities”. With these “coordinates” and “velocities”, we obtain the variation

of the gravitational action

which leads to the Lagrange equations,

with terms of the Lagrangian variation

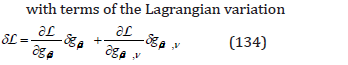
These equations suggest the definition of an energy pseudotensor

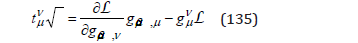
However, for the Lagrangian (131), from (B.7) we obtain

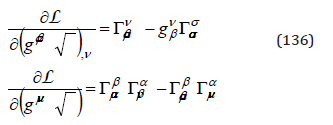
which suggest the definition of the energy pseudo-tensor

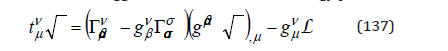
It is interesting that this change of coordinates, q_n →Q_m ,

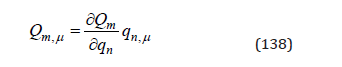
does not modifies the terms of the equation (135),

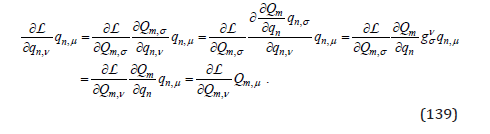
This means that the two expressions (135) and (137) define the same energy pseudo-tensor. With the expressions (88) of the metric tensor, and the expression

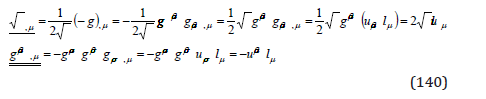
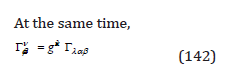
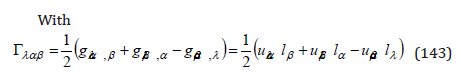
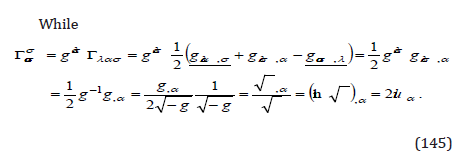
With the expressions (144), (145), and (141), the first term of the energy pseudo-tensor (137) is

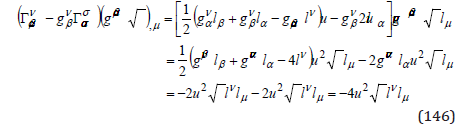
The second term of the pseudo-energy (137) is proportional to the Lagrangian

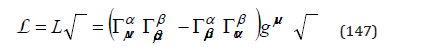
which, according to (C.7) and the normalization condition (89), is

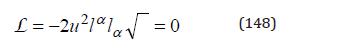
We notice that, according to (89), the pseudo-energy satisfies the normalization condition of a null trace:

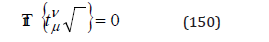
Non-zero elements arise only for a non-zero amplitude of a gravitational wave, as an acceleration field (91). When the amplitude is null, only a proper motion is described by the elements of the amplitude tensor in the invariant (118), which is the gravitational spin.

Relativistic Wave Equation of a Quantum Particle in Electromagnetic Field

In a flat space, corresponding to the special theory of relativity, the wave equation of a particle in electromagnetic field, the wave functions (30) take a simpler form

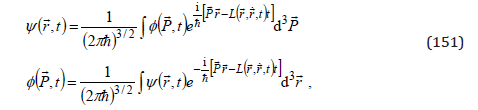
depending on time t, x⁰ =ct , the Lagrangian

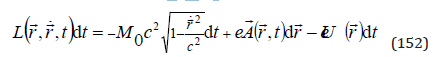
and the momentum

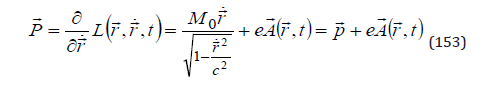
From the group velocity in the momentum space, we obtain the Lagrange equation

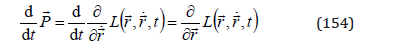
For an electromagnetic field with a time independent scalar potential as of an atom, and a time dependent vector potential as of a radiation field. It is interesting that, in this case, we obtain time the Hamiltonian as a function not explicitly depending on time, but only on coordinate velocity - the energy:

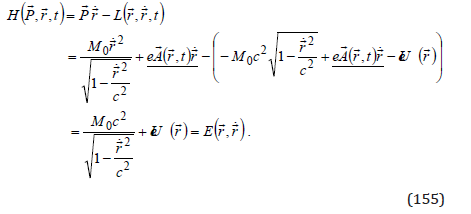
From (153), we obtain the velocity dependent term of the energy as a function of the canonic potential, which is the eigenvalue of the quantum momentum operator,

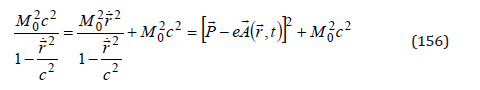
We obtain the relativistic Hamiltonian

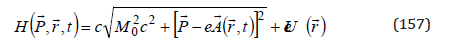
while, with (155), the particle wav function (151) takes the form

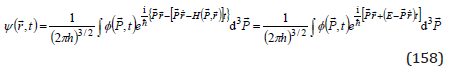
We obtain the relativistic wave equation

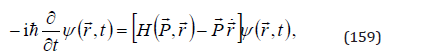
which depends on the momentum operator

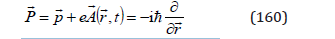
With the total time derivative

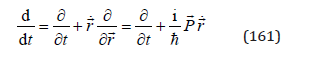
we obtain the relativistic wave equation of the form of the Schrödinger equation, but with the minus total time derivative instead of the partial time derivative of the wave function, and the relativistic Hamiltonian:

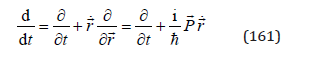
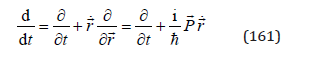
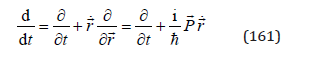
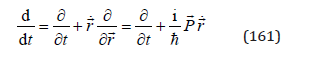
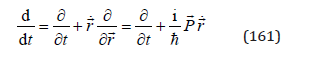
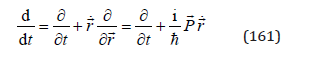
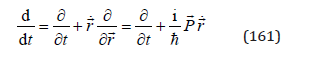
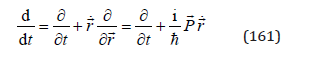
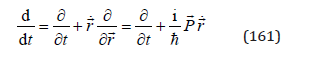
For these components, from (166) we obtain the explicit system of equations

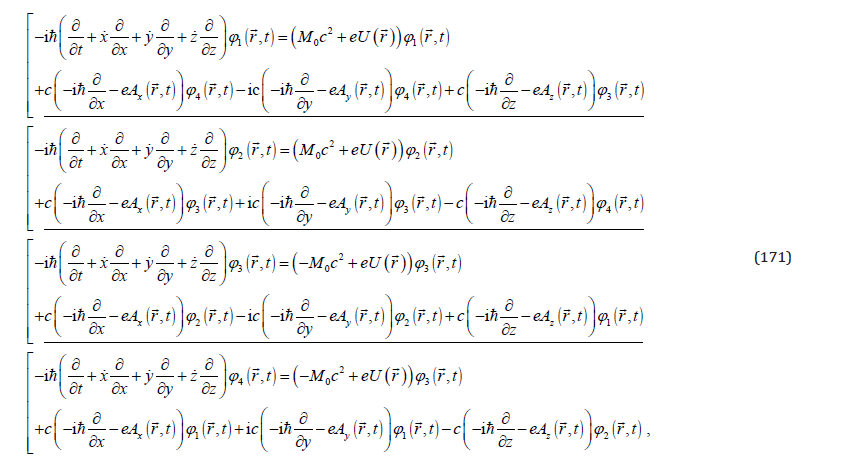
depending on the rest energy, velocity, and the electromagnetic potentials.

Summary

We considered a quantum particle with a mass M0 , as a continuous distribution of matter in a curvilinear system of coordinates, with a density positively defined as the square of the absolute value of a complex function. As a description of the matter dynamics, we defined a velocity field and showed that, according to the general theory of relativity, any covariant acceleration of a matter differential element, under the action of an external field, is perpendicular to this velocity. This means that the matter moves in planes perpendicular to the velocity, and that, for the complex We considered the matter conservation, and obtain a dynamic equation for velocities, depending on the metric tensor elements. When, in the equation of a gravitational wave, we consider a metric tensor of the second degree in coordinates, from the dynamic equation we obtain a harmonic oscillation of a differential element of matter. In this case, the metric tensor is proportional to an amplitude tensor, and a polarization tensor which satisfies a normalization condition. When we consider a metric tensor of the first degree in coordinates, we obtain an acceleration of a matter differential element. In this case, the metric tensor is also proportional to an amplitude tensor, but with a polarization vector, which also satisfies a normalization condition. For an amplitude tensor, we defined a scalar we called gravitational wave amplitude. In both cases, of a first-order solution, or of a second-order solution, the acceleration is proportional to this amplitude. For the amplitude tensor of a first-order solution of the metric tensor, we obtained a gravitational invariant, as a sum of the square of the gravitational amplitude plus two terms which, by rotation, transform one another. When the gravitational wave amplitude is null, no acceleration is present, while the two terms, describe an inner motion of the matter, we call spin. We obtain the gravitational spin 2 as an eigenvalue of the rotational angular momentum.

We considered the gravitational action as a time-space integral of the total curvature with the scalar density and obtained a Lagrangian depending on the elements of the metric tensor, and the derivatives of these elements with the contravariant coordinates. We defined a pseudo-tensor of energy, proportional to the square of the gravitational wave amplitude, which satisfies the normalization condition of a null trace.

In a flat space, for wave functions defined in a time-space system of coordinates, we obtained a relativistic wave equation of a quantum particle in electromagnetic field. Unlike the conventional Schrödinger-Dirac equation, instead of the partial time derivative of the wave function this equation contains the minus total time derivative, which includes an additional dependence on velocity. These differences appear from dependence of the time dependent phases of the wave functions on the Lagrangian, as the product of the momentum with the velocity minus the Hamiltonian, instead of the Hamiltonian in the conventional Schrödinger- Dirac equation. We obtained an explicit system of equations for the four components of the wave function, describing the velocity dependence of the particle dynamics.

References

1. Hall MJW, Reginatto M (2016) Ensembles on Configuration Space - Classical, Quantum, and Beyond. Fundamental Theories of Physics p. 184.
2. Barret R, Delsanto PP, Tartaglia A (2016) Physics: The Ultimate Adventure.
3. Plotinsky A (2016) The Principles of Quantum Theory, From Planck’s Quanta to the Higgs Boson. The Nature of Quantum Reality and the Spirit of Copenhagen.
4. Rowlands P (2015) The Foundations of Physical Law. World Scientific p. 264.
5. Baggott J (2015) Origins. The Scientific Story of Creation, Oxford University Press, UK.
6. Cox B, Forshaw J (2012) The quantum universe, Boston: Da Capo Press.
7. Smolin L (2006) The Trouble with Physics: The Rise of String Theory, the Fall of a Science and What Comes Next. ALLEN LANE an imprint of Penguin Books.
8. Penrose R (2004) The Road to reality. London: Vintage Books.
Brody TA (1993) The Philosophy Behind Physics. Berlin and Heidelberg: Springer-Verlag.
9. Stefanescu E, Scheid W, Sandulescu A (2008) Non-Markovian master equation for a system of Fermions interacting with an electromagnetic field. Annals of Physics 323(5): 1168-1190.
10. Stefanescu E (2010) Master equation and conversion of environmental heat into coherent electromagnetic energy. Progress in Quantum Electronics 34(6): 349-408.
11. Stefanescu E (2013) Open Quantum Systems of Particles and Principle 2 of Thermodynamics. Journal of Physics: Conference Series 413.v
12. Stefanescu E (2014) Open Quantum Physics and Environmental Heat Conversion into Usable Energy, Sharjah (UAE), Brussels, and Danvers (Massachusetts, USA): Bentham Science Publishers.
13. Stefanescu E (2017) Open Quantum Physics and Environmental Heat Conversion into Usable Energy 2, Sharjah (UAE): Bentham Science Publishers.
14. Stefanescu E (2012) Quantum Injection Dots. Fingerprints in the Optical and Transport Properties of Quantum Dots Edited by Ameenah Al-Ahmadi, INTECH, 299-34.
15. Stefanescu E, Cornescu LE (2009) Longitudinal Quantum Heat Converter. US Patent Office US20090007950.
16. Stefanescu E, Cornescu LE (2009) Quantum Injection System.US Patent Office US20090007951.
17. Stefanescu E, Cornescu LE (2010) Transversal Quantum Heat Converter. US Patent Office US20100019618.
18. Stefanescu E (2014) The relativistic dynamics as a quantum effect. Journal of Basic and Applied Research International 1(1): 13-23.
19. Broglie L (1932) Theory of Quantification in the New Mechanics, Paris: Hermann et Cie.
20. Heisenberg W (1949) The Physical Principles of the Quantum Theory. Dover Publications, Inc, New York, USA.
21. Pagels HR (1983) The Cosmic Code: Quantum Physics as the Language of Nature. Toronto, New York, London, Sydney: Bantam Books, USA.
22. Stefanescu E (2017) Relativistic Dynamics, Electromagnetic Field, and Spin as All Quantum effects. Journal of Electronic Science and Technology 15(4): 333-341.
23. Stefanescu E (2016) Semiconductor Structure Converting Environmental Heat into Usable Energy. Energy Materials Nanotechnology Meeting on Spintronics: October 10-14, 2016 Las Vegas, USA.
24. Stefanescu E (2017) Electromagnetic field, spin, and gravitation, as characteristics of a charged quantum particle wave function. 2^nd International Conference on Physics: August 28-30, 2017 Brussels, Belgium.
25. Stefanescu E (2017) Quantum master equation for Fermions and a unitary relativistic quantum theory. 2^nd International Conference on Quantum Physics and Quantum Technology 25-26, Berlin, Germany.
26. Stefanescu E (2017) Unitary relativistic quantum theory. 3^rd International Conference on Theoretical and Condensed Matter Physics: October 19-21, 2017 New York, USA.
27. Kregar A (2011) Aharonov-Bohm effect, University of Ljubljana, Faculty of Mathematics and Physics, Department of physics, Seminar 4, Ljubljana.
28. Dirac PAM (1975) General Theory of Relativity. New York, London, Sydney, and Toronto: John Wiley & Sons, New York, USA.
29. Einstein A (2008) The Meaning of Relativity, London and New York: Routledge Classics.