Research Article

A Novel Empirical Approach to Estimate the Acoustic Properties of Smart Materials: Part I

Federico Cecchini^1,2, Francesco Fabbrocino³, Massimo Bassan^4,5, Pietro Russo⁶ and Francesca Nanni^1,2 *

¹Department of Enterprise Engineering, University of Rome Tor Vergata, Italy

² Italian Interuniversity Consortium on Materials Science and Technology (INSTM), Italy

³Department of Civil Engineering, Pegaso University, Italy

⁴Department of Physics, University of Rome Tor Vergata, Italy

⁵ National Institute of Nuclear physics, Italy

⁶ Institute for Polymers, Composites and Biomaterials (IPCB), Italy

Submission: May 16, 2018; Published: July 02, 2018

*Corresponding author: Francesca Nanni, Department of Enterprise Engineering, University of Rome Tor Vergata, Italy, Email: fnanni@ing.uniroma2.it

How to cite this article: Federico C, Francesco F, Massimo B, Pietro R, Francesca N. A Novel Empirical Approach to Estimate the Acoustic Properties of Smart Materials: Part I. Academ J Polym Sci. 2018; 1(2): 555557. DOI: 10.19080/AJOP.2018.01.555557

Abstract

In this work, a novel empirical approach to the estimation of the rheological behaviour of smart materials from the sound insulation capabilities is proposed. The testing protocol relies on a small sound research facility that was designed with the goal of achieving a movable yet flexible measurement system, suitable for both laboratory environments and quality assurance departments.

Unlike other test protocols relying on lightweight acoustic research solutions, the proposed methodology was developed to perform acoustic tests in a diffused field environment, a test condition much closer to real life applications, and in a sufficiently wide frequency range (eg. 2 -10kHz).

The proposed test methodology was validated by means of modal analysis of the chamber and by comparison between empirical acoustical test results (insertion loss) and the expected theoretical results.

At last, as a proof of concept, it is showed how to apply the proposed protocol to the measurement of the sound insulation of a novel laminate containing a nano composite core and how to evaluate indirectly the rheological behaviour merely from acoustical data.

Keywords: Acoustics; QA; Smart materials; Sound-insulation

Introduction

The development of Smart materials, composite systems capable of altering their properties when subjected to external stimuli, has brought about a revolution in materials science and in modern society as a whole. In fact, smart materials can be designed basing on the requirements of a particular application and the response can be tailored up to the customer’s needs, thus allowing engineers to develop materials with many different functions embedded.

The alteration can be triggered either by means of autonomous modifications in the microstructure of the material (passive smart materials) or by means of external control systems (active or semi-active smart materials). The first class is based on non-Newtonian fluids such as Shear-thickening fluids, while the latter on magneto rheological and electro rheological fluids.

In particular, as smart materials can alter their vibration damping properties, they prove to be particularly interesting for acoustic applications in the aeronautical and automotive field, in which the acoustic comfort of the cabin interior is a major concern.

These advanced composites usually comprise non-Newtonian fluids encapsulated in a stiffer medium. In particular, as most smart materials are used in lightweight structures such as sandwich panels, smart materials are usually interposed as the core of laminates in constrained layer damping (CLD) configuration.

Furthermore, active or semi-active smart materials allow for the optimization of the performance of the material for a wide range of working conditions, as the associated control system modifies the acoustical response. The acoustical response of Smart materials is heavily influenced by the rheological response of non-Newtonian fluids at acoustically significant frequencies, typically in the kHz range. In practice, in order to evaluate the acoustical performance of a newly developed Smart material, as the maximum oscillation frequency of the most commonly available rheometers is less than 16Hz, regression methods to derive the high-frequency data from low-frequency rheological data must be employed.

These methods solve an ill-posed mathematical problem (Tikhonoff inverse problem), where acoustical data must be extrapolated from experimental rheological measurements with an unknown error [1,2]. These numerical methods to evaluate the acoustical response of smart materials, although tempting, are still undergoing intensive studies in various fields of research and typically require massive rheological experimental campaigns and the solvers are CPU intensive. In the second instance, these numerical methods only provide a first good estimate of the acoustical properties of the core, as the acoustical properties of the smart material are dependent on the boundaries and loads applied on the full structure.

As a consequence, as R&D laboratories often present the necessity of testing the outputs of the research right after the chemical synthesis of the material, it is desirable to find an empirical approach to provide a preliminary good estimation of the acoustical properties of the final sandwich structure.

Furthermore, as shown in previous works [3], sound transmission loss or insertion loss tests can be used as an alternative to other non-destructive tests (NDT) and can provide valuable information concerning the mechanical properties of CLD structures and structures that present adhesive joints or other permanent bonds as well.

In the following, a novel empirical approach to the evaluation of the sound insulation properties of smart materials will be proposed. This method will rely on the design of an Acoustic Properties Evaluation-Small Room Facility (APESR facility). The whole leitmotiv of the proposed design procedure relies on the extension of the measurable frequency range, the weight reduction of the structure and the maximisation of the versatility of the facility itself. Secondarily, the APE SR facility was designed in a modular way, with the possibility of joining it with another reverberation chamber or anechoic chamber.

This design choice in the future, can allow for changes in the sound test layout. Finally, it was taken into account the possibility of attaching a shaker [4,5], for forced-response vibroacoustic tests. In fact, during the design process, it was considered the necessity of achieving a sound research facility suitable for addressing both sound transmission loss and sound absorption loss, respectively by means of insertion loss (and/or transmission loss) test evaluations and sound absorption test evaluations.

While traditional sound transmission loss tests performed in standardized facilities require non-negligible amounts of materials for the test samples (up to 6square meters), the APE SR facility was designed trying to minimize the amount of material necessary for each test. ISO A3 samples were considered as a reasonable compromise between good measurements (the larger the sample, the better) and typical laboratory material production rates.

On the other hand, even though standard laboratory tests like the ones performed by using impedance tubes [6], require small samples, they only allow normal incidence sound fields and very narrow frequency bandwidths. Therefore, the design of the main body of the reverberation chamber is characterised by some main critical factors: volume of the acoustical cavity, shape of the cavity, surface finish of the internal surface and effect of the closing wall.

The interior volume of the small reverberation chamber introduces limitations as far as the analysis at lower frequencies is regarded. This can be traced back to the modal response of the air volume, characterized by highly superposed and singularly undistinguishable modes. The lower limit to the beginning of this chaotic dynamic response is given by the Schroeder frequency, which is inversely proportional to the air volume contained inside the reverberation chamber.

Below this lower limit, the absolute results of the sound insertion loss and sound transmission loss tests are not reliable, but the experimental data can however be useful for comparative tests. The shape of the cavity affects the modal distribution: the more irregular, the more homogeneous the distribution. However, more complex shapes tend to reduce the stiffness to weight ratio of the structure, thus limiting its mobility and requiring higher production costs.

On the other hand, the surface finishing influences the cut-off frequency of the measurable frequencies. Finally, the dimension of the opening window, which doubles as a sample holder for insertion loss tests, influences the measurements because smaller samples tend to resent more of the boundary effects. In other term, it must be found a good compromise for the sample dimension: the larger the sample, the more negligible are the boundary effects and the more material is required in order to perform each test.

All of these factors will be analysed at great lengths in the following.

Theory/Calculation

Insertion loss measurements

The sound insulation properties of a material can be indicated by means of the sound transmission loss (STL) parameter. This parameter, expressed in the dB scale, can be derived from the acoustic transmissibility as follows.

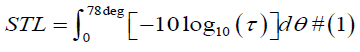
As an example, for a CLD sandwich with skins named 1 and 2, can be estimated as follow

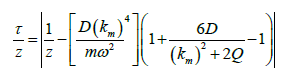
With:

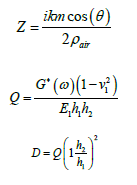
Where:

i. k is the wave number.

ii. θ is the integration angle that varies from 0deg to 78deg. This particular value derives form numerical considerations, as the contribution of angles higher than this are negligible to the sound insulation properties of the panel [7].

iii. Z is the acoustical impedance.

iv. m is the surface density of the panel.

v. air ρ is the density of air.

vi. G∗ (ω ) is the frequency dependent complex shear modulus of the core.

vii. h is the thickness.

viii. v is the Poisson modulus.

Theoretically, if all parameters are known, the STL can be estimated from low-frequency rheological data by substituting the frequency dependent shear modulus in the equation.

However, as this parameter requires a rather complex numerical regression, it is possible to provide a first estimate of the sound insulation properties of a polymer by extrapolating the shear modulus form the measured STL spectrum. This spectrum can be measured by means of a sound insertion loss (IL) test.

In this case, the test will be performed by employing opportunely baffled samples inserted in a modified reverberation chamber.

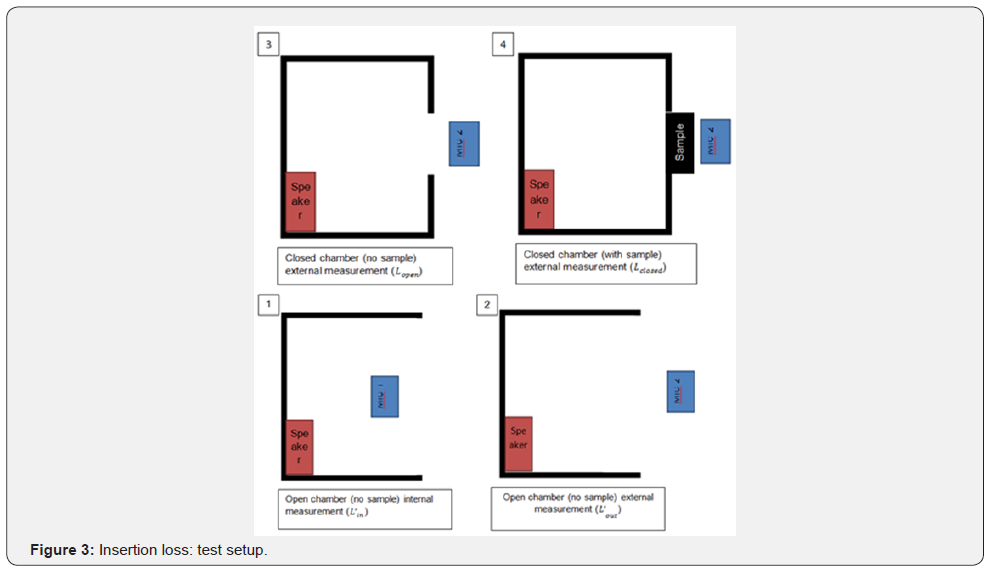
In general, the IL evaluation is based on the measurement of the sound pressure field in four different configurations:

i. Front wall open + internal microphone in L_in^'

ii. Front wall open + external microphone L_out^'

iii. Front wall closed (no sample) + external microphone L_open^'

iv. Front wall closed (with sample) + external microphone L_closed^'

v. The sound transmission loss of the sample is equal to (Figure 1 & Figure 2):

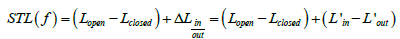
Preliminary considerations

The main global design prerequisites for the reverberation chamber can be resumed as follow:

i. Minimal amount of space required for the whole structure (accessories and base frame included).

ii. Minimal wall thickness imposed by the necessity of sound insulation inside the chamber and stiffness of the structure during the construction and transport phases

iii. Shape of the cavity motivated by the desire to homogenize the natural mode distribution on the whole spectrum

iv. Maximisation of the internal volume in the chamber, in order to minimize the lower measurement limit imposed by the Schroeder frequency [7-10];

v. Minimum porosity of the internal surface, in order to increase the cut-off frequency of the structure [11].

Before proceeding, it was considered as a minimum acceptable frequency range for sound insulation measurements 2000-10000Hz, compatible with many engineering applications of industrial interest, from an acoustical perspective.

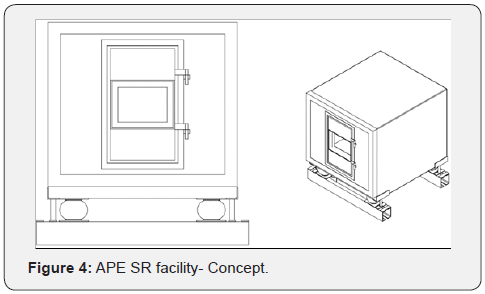
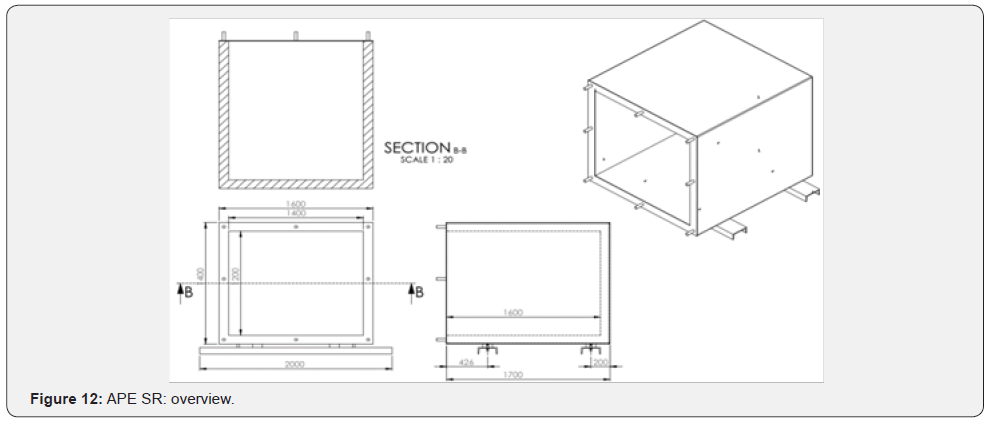
Taking into account the previously listed requisites, it was chosen for the main body of the reverberation chamber a concrete cube with a cavity on the front side (Figure 3). The front side presents threaded wire for a secure attachment of the closing wall or the second reverberation/anechoic chamber.

On a side note, even if opportunely shaped hexahedral cavities were proven to provide a more uniform distribution of the natural frequencies [12], the internal cavity of the APE SR was shaped as a rectangular parallelepiped, because of the better stiffness to weight ratio of the structure of the latter solution and, as a consequence, higher manoeuvrability. For the base of the reverberation chamber, it was chosen a frame connected to pneumatic vibration isolators (4Hz cut-off frequency).

These last structural elements, interposed between the frame and the main body of the reverberation chamber, serve the purpose of decoupling the structure from the external environment, in order to minimize the external influences (i.e. floor vibrations, shaker induced structure borne vibrations) during the measurement phase. The closing wall is fashioned with the same goal of achieving a multi-purpose structure and presents a movable inspection panel, with a detachable sample holder, allowing a “clamped” boundary condition. We installed ulterior threaded wires for attaching the measure apparatus (i.e. omnidirectional microphone) and a secondary anechoic chamber; both used in transmission loss (TL) and insertion loss (IL) evaluations.

Design and optimization of the APESR facility

Staring from the solution of Helmholtz’s equation, it is possible to evaluate the distribution of the modes of the system [13-16].

Taking into account the infinitely rigid boundaries, we can assume that the wall specific impedance is infinite and the velocity field at the boundaries is null.

In a Cartesian reference system with axis parallel to the sides of the enclosed cavity:

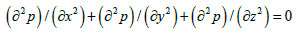
By substituting the trial solution p( x ,y, z) = p_x( x) p_y( y) p_z( z) into the wave equation(1), this is decomposed into three analogous ordinary differential equations (ODE), where the only difference is in the coordinates (x in the first, y in the second and z in the third one). The same consideration is verified for the rigid wall boundary conditions (BC). From now on, the discussion will be focused on the first ODE and its BC (the one in the x coordinate), but the obtained results can be easily inferred for the other two equations.

The function P_x , in order to be physically acceptable, must verify the following conditions (2):

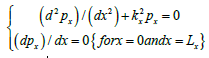
Where L_x denotes the base width, considering the origin of the reference systemlocated in a vertex of the base rectangle.

The three orthogonal components of wave numbers k must satisfy the following condition:

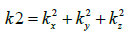
The solution of the first ODE can be written as: p_x( x)=A₁cos(k_xx=B₁kx_x)

In order to satisfy the imposed BCs, 1 B = 0 and K_x = (n_x π)/ L_x where n_x is a generic natural number.

By substituting these last equations (and the analogous ones for K_y and K_z into equation (3), we obtain:

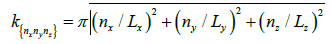
Associated to the eigenvectors, we can evaluate the functions:

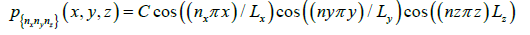
Where C is an arbitrary constant which satisfies the boundary conditions.

Finally, the associated eigen frequencies of the air cavity are:

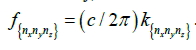
At this point, it is possible optimizing, from an acoustical perspective, the shape of the cavity considering the following constraints:

i. Maximum stiffness-to-weight ratio of the structure

ii. Maximum Schroeder’s frequency

iii. Uniform distribution of the eigenfrequencies

iv. Construction simplicity.

Taking into account the average distance between two successive eigenmodes

and the variation in frequency

of the Δf -nth eigen mode from the average value, this last constraint imposes the minimization of the index

, indicating the homogeneity in the distance between different mode shapes.

This constrained optimization was further refined by Blaszak’s method [9,17], consisting in the minimisation of a secondary index

This simultaneous constrained optimization, carried out while taking into account the ease of construction of the structure and other technological constraints, led to the design shown in the following schematics (Figure 4):

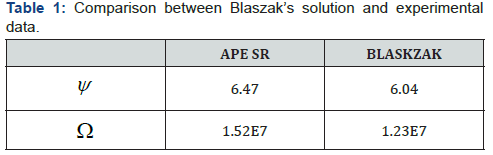
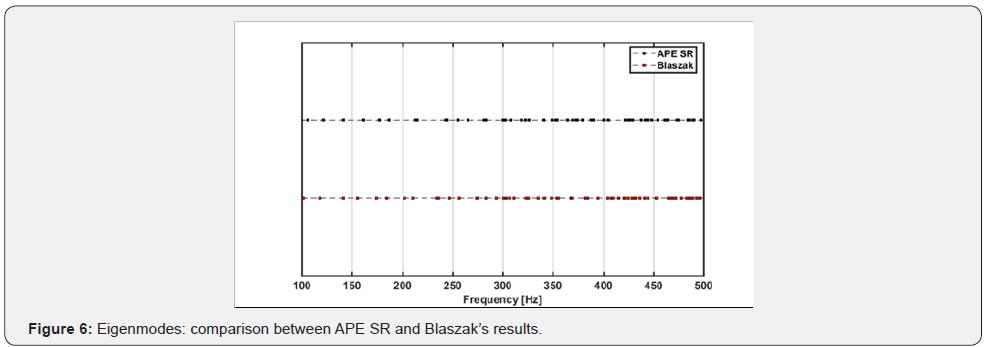
This results rounds down Blaszak’s proportion fora reverberation chamber with walls characterised by an average acoustic absorption of α ≈ 0.01(1:1.2 :1.4). The differences between Ωψ for the two solutions are shown in the following table (Table 1):

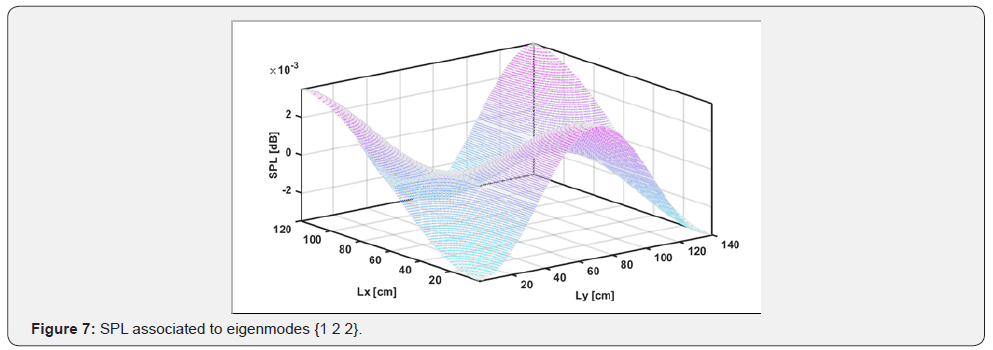
The differences between the proposed design and Blaszak’s optimised design in terms of eigenmodes distribution can be shown in the following graph (Figure 5). The graph considersa hypothetic reverberation chamber with internal dimensions of 1.20mx1.44mx1.68m (which accords to Blaszak’s proportion). By substitutingthe eigenmodes inside the Helmholtz’s equation, it is possible to evaluate the acoustic pressure field for the various eigenmodes. For example, in the following Figure 6, it is shown the sound pressure level (SPL) in the x-y plane at z=50 [cm] associated toeigen modes {1 2 2}.

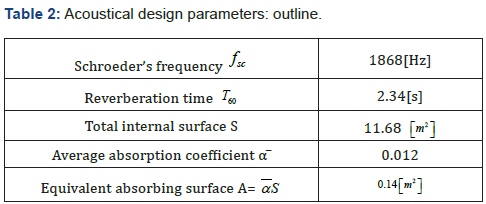
From a merely qualitative perspective, it can be noticed that the regions where the sound pressure level is null coincide with the projections of the nodal planes on the x,y plane. In conclusion, the acoustical design parameters can be summarized in the following (Table 2).

Construction of the sound research facility

The material chosen for the construction of the reverberation chamber was reinforced concrete, because of the low cost, low acoustic absorption and high density. This last parameter influences the acoustic insulation properties and the seismic mass of the system: the higher the density, the better the sound insulation. The reverberation chamber was manufactured by using a mix design of Portland cement (type II/A-LL 45,2R) and finely grinded sand which was compacted both by ultrasonic means (needle compaction) and external means (vibrating plate compaction). This process was carried out in order to maximize the sound reflection and minimize the absorption caused by local Helmholtz resonator effects.

This acoustical mechanism can be traced back to the microporosities naturally present in concrete-based structures. In order to reduce the sound absorption of the concrete, the interior of the cavity was furtherly coated with a thin layer of stucco. The concrete was reinforced with an electro-soldered steel net with the following characteristics (Table 3).

Because of the necessity of rotating the structure once the concrete dried, the reverberation chamber was designed with a reinforced bottom, with two electro-soldered nets Figure 7 and an increased wall thickness of 200mm [18]. The structure was removed from the mould after 2days and the concrete was left to maturate for 30 days before the rotation (see rotated APE SR in Figure 8), in order to increase its compression strength up to 42.5MPa and to minimize the risk of failure.

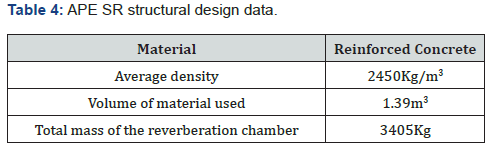
The design data can be resumed in the following table (Table 4):

In order to decouple the dynamic response of the reverberation chamber from the floor vibrations [19-21], for the suspension system were used 4 pneumatic suspensions (Figure 9), each one with a load bearing capability up to 1600kg at 7 bar [22]. The whole assembled structure is shown in the following (Figure 10).

The schematics of the reverberation chamber, excluding the sample holder and inspection panel, is reported in (Figure 11).

In order to validate the chamber and the measuring system different materials were used.

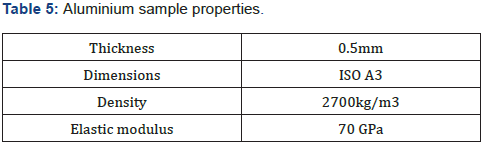
In the case of insertion loss, instead, an aluminium alloy plate Al 6060, with the following characteristics (Table 5) was employed:

Finally, after chamber validation, measurements of a sandwich in constrained layer damping configuration, were carried out in order to assess its acoustic properties. At this regard, the damping layer was prepared by mixing a Polyethylene Glycol 200g/mol (Sigma Aldrich) with a 20% by weight of 12nm fumed silica (Sigma Aldrich), while the outer skins were two plates of Al6060 with a thickness of 0.5mm.

The colloid was prepared by recurring to the following approach [23]:

i. The powders were dried in an unventilated oven (8h-50 °C).

ii. The powders were dispersed in intermediate carrier and the resulting slurry was subsequently dispersed in excess solvent.

iii. The slurry was magnetically stirred at ambient temperature and then in an ultrasonic bath.

iv. The agglomerates were dispersed in the carrier fluid by jar-stirring.

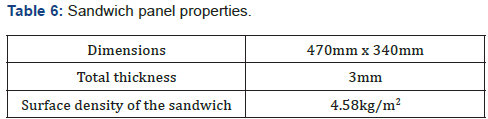
The sandwich used exhibits the following characteristics (Table 6).

Experimental

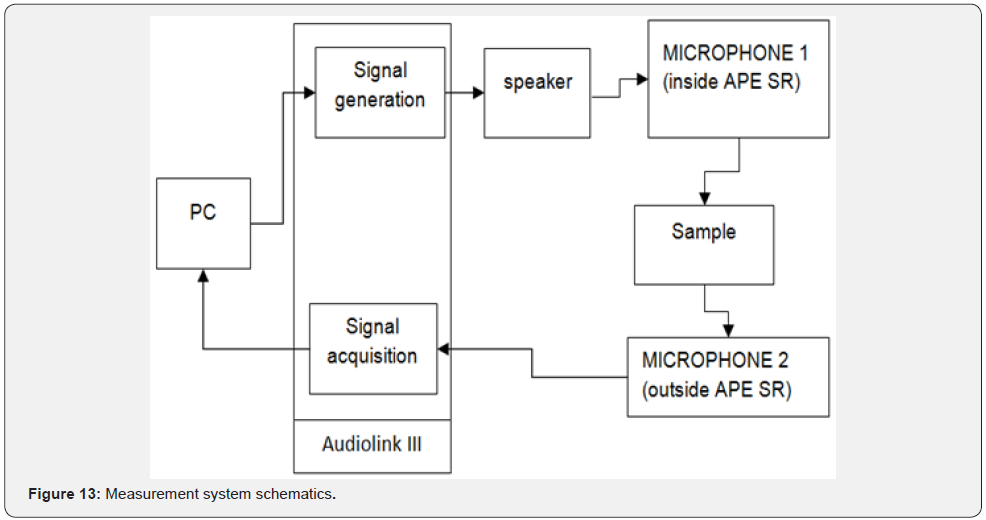
The measurement system annex to the facility and used in the various acoustical characterisation (insertion loss, absorption loss) consists of:

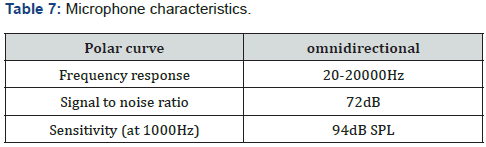
i. Two laboratory microphones Super lux ECM 888 B ¼’’ with the following characteristics (Table 7).

ii. An 80-watt speaker with a flat frequency response (without a prevailing frequency content) between 50Hz and 20000Hz.

iii. A dual mode acquisition card Midtech Audiolink III (two microphone input-ports and a STEREO or dual MONO audio output-ports).

The measurement system (Figure 12) is connected as follows.

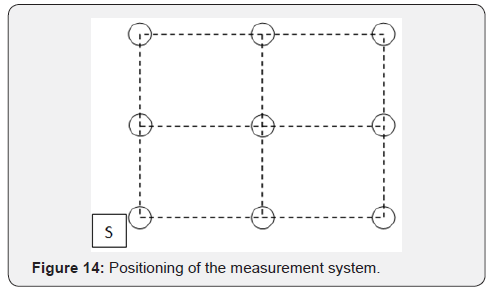
The proposed design of the APE SR reverberation chamber was validated and compared to the previous analytical results. The speaker was located in a fixed position while the microphone was relocated in 9 different positions (indicated as white circles in the following Figure 13) in the x-y plane at the same height z=h/2=1200 mm/2=600mm. During the validation, the sample holder was momentarily closed with a concrete panel and completely sealed with a layer of sealant.

The input signal generated was a sine sweep wave with a linearly variable excitation frequency from 20Hz to 20kHz and constant unitary amplitude, maintained for 10seconds. The effective SPL inside the chamber was recorded by the microphone in each of the 9 configurations and post-processed with the commercial software Fuzz Measure.

The post-processing is divided into the following phases:

i. Deconvolution of the audio signal, in order to evaluate the system response to the excitation wave.

ii. Fast Fourier transform (FFT) of the time history data, in order to evaluate the response in terms of frequency and SPL [dB].

iii. Evaluation of the actual reverberation time of the structure and its dependence on frequency.

The Deconvolution is necessary to evaluate the response of the system to the excitation, in order to filter the signal from the background noise innate to the measurement system and to calculate the FFT. This allowed us to evaluate the SPL in 9 different microphone positions (indicated by the thin coloured lines) of the reverberation chamber.

In the following graph (Figure 14), the envelope of the 9 curves is represented by a bold black line. The signal was smoothed choosing 1/3 octave bandwidth smoothing (Figure 15).

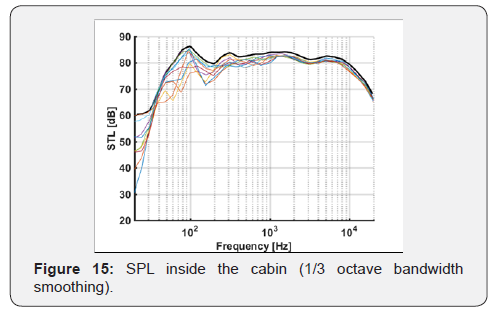
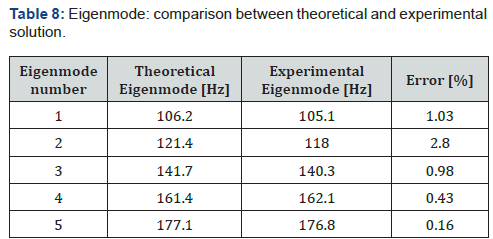
By observing the data, it can be acknowledged the existence of a region approximately below 100Hz where the SPL inside the chamber reaches a minimum. This is caused by the first resonance of the chamber, which occurs at approximately 106Hz. Before this frequency there are de facto no reflexions and the sound pressure level varies significantly from point to point inside the chamber and assumes low values. Between 100 and 500 Hz the SPL is highly variable from point to point and the response is highly dependent on frequency: this is caused by the higher eigenmodes.

By analysing the envelope of the SPL curved, it is possible to compare the theoretical eigenfrequencies, calculated by Helmholtz’s equation, and the experimentally measured ones (Table 8):

Roughly above 700Hz the SPL envelope curve approximates a quasi-linear trend and the nine curves tend to coincide. This phenomenon is an indicator of the fact that the sound power inside the chamber is almost constant above this frequency. As a consequence, this signals the passage from a system whose dynamics are dominated by its modal response to a more desirable condition of diffused acoustic field.

Also in this case, there is good accordance with the theoretical value for Schroeder’s frequency. Taking into account that 1000Hz is the central frequency of the octave bandwidth 710Hz-1420Hz, we can notice graphically that the diffused field in the APE SR facility occurs approximately between 700Hz and 1000Hz: this limit denotes the inferior limit of validity of the successive results for the STL of the tested samples.

As it can be noticed, between 9000Hz and 20kHz the SPL decreases, even though it is still maintained the diffused acoustic field condition. This reduction in the SPL is caused by the microporosities in the concrete, which act as microscopic Helmholtz resonators at higher frequencies.

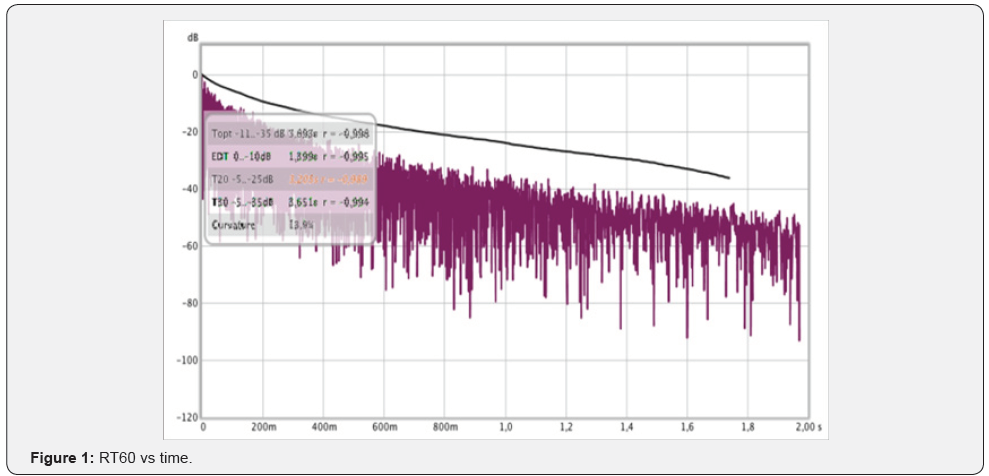
This variation is however limited to 2-3dB up to 15kHz and, therefore, can be considered negligible. Because of the complexity associated with the calculation of the reverberation time RT60, it was chosen to extrapolate this parameter from the T20, a conceptually analogous parameter, which is evaluated for an attenuation of 20dB instead of the 60dB required for the previous parameter. In fact, in order to calculate the RT60 it is first necessary to calculate time necessary to have a 60DB attenuation in the sound energy density D(t) [dB].

However, even though theoretically possible, the calculation of this value is nontrivial, in particular in small room acoustics where the dynamic range, nominally the difference between the maximum value of D(t) and its asymptotic value, is much smaller than 75dB. This particular value has been demonstrated empirically [24] to be the threshold value of this parameter necessary to actually measure and attenuation of 60 dB and therefore, to evaluate, the RT60. Therefore, according to the norm ISO 3382, the reverberation time was calculated basing on the evaluation of a parameter requiring an inferior dynamic range.

The starting point for the refining of the analysis was the measurement of D(t)=20 log(h(t)/max[h(t)]) where h(t) is the envelope of the excitation H(t).

D(t), represented as a thin purple line in the following picture varies between 0 dB and the value corresponding to the sound energy density of the background noise.

On the other hand, the Schroeder’s integral

is represented as a bold black line in the graph.

From Schroeder’s integral, it is possible to derive a linear extrapolation of the reverberation times, by considering a linear relationship r = A∗t + B ,where A is the slope and B is the expected attenuation.

Therefore 60 RT = −60 / A, where A is evaluted from the experimental measurement of the T20.

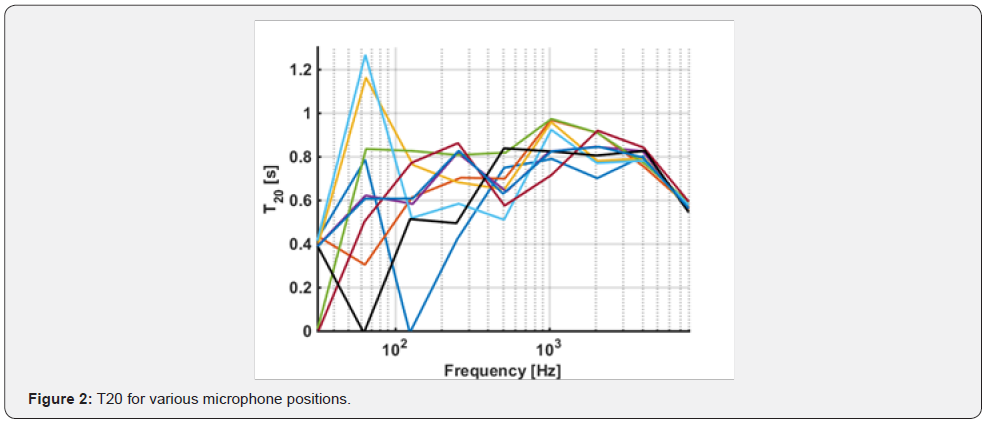
The results for the T20for the various positions of the microphone at the centre frequency for each octave band width can be shown in the following graph (Figure 16):

The extrapolated experimental value for RT60 is 2.34s, which coincides with the value theoretically expected from Sabine’s formula.

Results and Discussion

The first step to evaluate the sound transmission loss of the system was the evaluation of the system in the first two configurations. The samples were all be tested with the baffled boundary condition and a white noise signal (a random signal having a constant power spectral density). This value is an index of the influence of the closing wall to the sound pressure level effectively perceived by the sample (Figure 17). The results with a 1/3 of octave bandwidth smoothing showed that this value attests at around 10dB after the diffused field condition is established. This parameter is extremely relevant in the case of the APE SR, because of the reduced size of the sample holder, which causes a non-negligible boundary effect contribution to the IL.

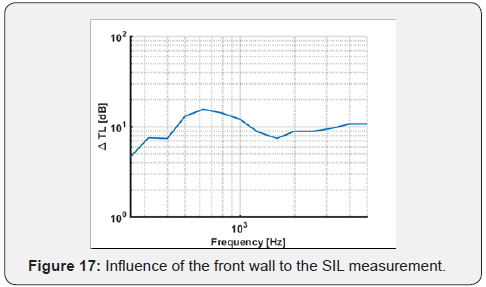
For the proposed design, the minimum sample dimension was reduced to a ISO A3 standard, much smaller than the 6m2 required for traditional transmission loss testing and therefore this parameter is non-negligible to the system response. Once the system was set, it was possible to compare the numerical expected results for a simple system, whose vibroacousticresponseis widely known in the currently available literature (i.e. aluminium plate) with the measured ones.

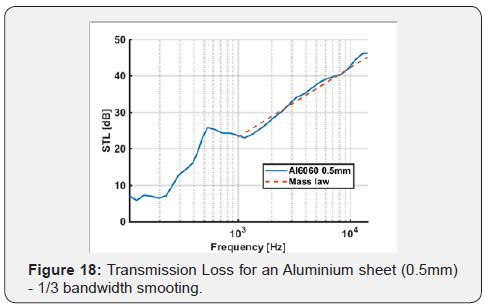
As it can be seen (Figure 18), the experimental results are adherent to the theoretical ones in the diffused field region, as expected. We can therefore consider the system fully validated and we can consider reliable the results for our measurements between 700 and 15000Hz. Below 700Hz, as previously discussed, there is a highly instable zone characterized by the presence of both the modal response of the chamber and of the resonance of the material.

However, it is still possible to identify the stiffness-controlled zone of the response of the system at approximately 100Hz and the damping-controlled zone between 200Hz and 1000Hz, as expected by the theoretical results [25-28].

With the fully validated system, the same analysis was repeated, as a proof of concept, for a sandwich structure in constrained layer damping configuration, realized as previously described in the Materials section. First of all, we carried out the rheological analysis of the nanocomposite previously described, by recurring to the following rheological approach.

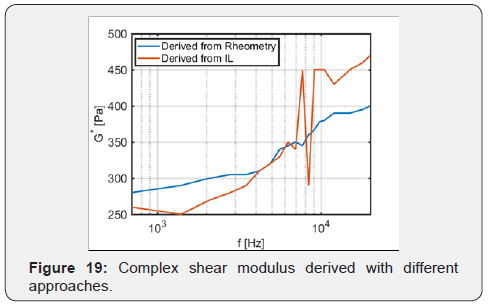
We carried out an steady-shear rheological measurement with a Strain-controlled rheometer (Kinexus LabPro+). The chosen fixture was a conical plate with a 0.8mm gap between the sample and the lower end of the fixture. A 1 minute 1s{ 1} − shear rate was applied to each sample (25ml), to break-pre-existing gel structures and therefore, to be able to neglect pre-existing stress fields in the fluid. The shear strain varied between 1 % and 120 %. This allowed us to pre-screen the properties of the fluid that exhibits a shear-thickening Non-Newtonian behavior (Figure 19).

However, as these materials are rheologically complex and do not obey to Delaware-Rutgers’ rule [29], to fully model the acoustic constitutive behavior of this material requires further research. Furthermore, Time-temperature superposition techniques, such as WLF, generally provide unreliable constitutive behavior at higher frequencies [30,31].

In order to fully model and analyse the vibroacoustic response of the sandwich at acoustic frequencies and the dependence on the composition of the nanocomposite, further investigation is required for the rheological response of the polymer at acoustic frequencies [1,32]. By iterating the Insertion loss measurement method reported above, it was possible to calculate the sound insulation properties for the proposed sandwich material (Figure 20 & 21):

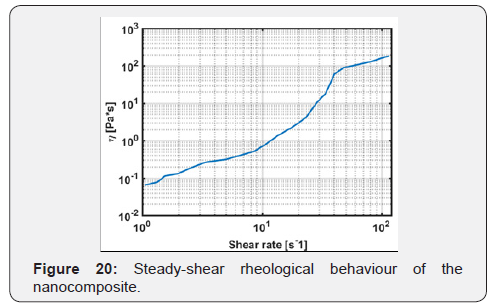
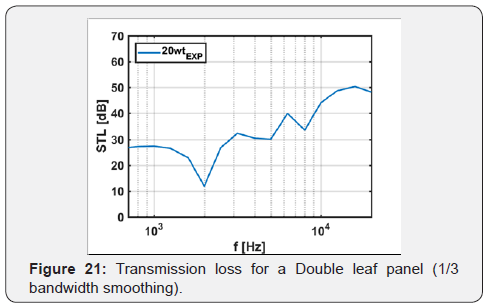
Between 2200Hz and 10000Hz shows a step increase in the STL, before experiencing a progressive decrease in the sound insulation properties. This is caused by the high-frequency response of the proposed material composing the constrained damper [7,33-36]. The decrease in the STL of the sandwich can be ascribed to the reduction in the damping of the core at higher frequencies, which occurs in the sandwich nearby the coincidence frequency. In this range its response is actually dominated by the damping of the system, in accordance with the previous results.

Finally, the complex shear modulus can be derived from the STL. In both cases, as typically expected for STFs, the complex shear modulus increases with frequency. As a comparison, the results for the numerical extrapolation proposed in [23] are compared with the ones extrapolated from equation 1 in (Figure 19). The linearly extrapolated shear modulus provides a good matching with nonlinearly extrapolated one for lower frequencies. However, the values tend to deviate from one another as the frequency increases. This can be traced back both to errors in the non-linear regression and in the experimental measurement, that tend to increase at higher frequencies. Further research is due.

Conclusion

The objective of this work was the development of a empirical approach to evaluate the rheological behaviour of smart materials. This method required the design of a small acoustic research facility, optimized for laboratory environments and quality assurance laboratories.

The structure was designed as a flexible tool, usable for the evaluation of the sound insulation of innovative composite materials in diffused sound field conditions, which cannot be achieved in conventional acoustic laboratory equipment such as impedance tubes there are standard test methods for the determination of these properties. There is, however, no standard for the equipment used in these tests, only a specification for the test conditions. The objective of this work was to evaluate the operation and performance of a bench top laboratory sound testing system for its potential as a simple cost effective method for the initial evaluation of materials that require specific acoustic properties. The work was limited to an investigation of the property of sound transmission loss (STL(6)(6)(5)(5)(6)(6)(6).

As a consequence, the structure was designed taking into account:

i. The maximisation of the stiffness to weight ratio of the structure and its movability

ii. The reduction of the required dimension of the samples (from 6m2 to an ISO A3).

iii. The maximisation of the frequency ranges of analysis, up to 700Hz-15000Hz.

The reverberation chamber, built in reinforced concrete according to these guidelines, was validated by testing the insertion loss of an aluminum alloy plate Al 6060. The achieved results showed a good agreement with datasheets of investigated samples.

Further experimental tests demonstrated the potential use of the chamber to assess the vibroacoustic behavior of structures comprising smart materials. At this regard, preliminary measurements carried out on a system constituted by aluminum skins and a core including fumed silica nanoparticles highlighted interesting perspectives of the new acoustic facility to investigate nano structured systems that can be used as damping materials as well as its actual reliability. Finally, the complex shear modulus extrapolated from acoustical data was compared with the one obtained by means of non-linear regression of rheological data from low-frequency data.

References

1. Cecchini F, Fabbrocino F, Cherubini V, Nanni F (2017) Numerical modeling of a Composite pentamode comprising a shear-thickening fluid. Int J Mason Res Innov.
2. Cecchini F, Cherubini V, Nanni F (2016) A D.O.E. analysis of the rheological properties of non-Newtonian fluids with different compositions. ECNP IX.
3. Malakooti S, Mohammadi N, Mahjoob MJ, Mohammadi K (2010) Identification of Adhesive Bond in A Multi-Layered Structure Via Sound Insulation Characterestics. J Mech 26(3): 363-372.
4. Fabbrocino F, Farina I, Modano M (2017) Loading noise effects on the system identification of composite structures by dynamic tests with vibrodyne. Compos Part B Eng 115: 376-383.
5. Modano M, Fabbrocino F, Gesualdo A, Matrone G, Farina I, et al. (2015) On the forced vibration test by vibrodyne. COMPDYN 2015 - 5th ECCOMAS Themat. Conf. Comput Methods Struct Dyn Earthq Eng.
6. Allan PSS, Ahmadnia A, Withnall R, Silver J (2012) Sound transmission testing of polymer compounds. Polym Test 31(2): 312-321.
7. Assaf S, Guerich M (2008) Numerical Prediction of Noise Transmission Loss through Viscoelastically Damped Sandwich Plates. J Sandw Struct Mater 10(5): 359-384.
8. Schroeder MR (1996) The Schroeder frequency revisited. J Acoust Soc Am 99: 3240.
9. Błaszak MA (2008) Acoustic design of small rectangular rooms: Normal frequency statistics. Appl Acoust 69(12): 1356-1360.
10. Rossing TD (2007) Springer Handbook of Acoustics, Switzerland.
11. Nagler L, Rong P, Schanz M, Estorff O von (2013) Sound transmission through a poroelastic layered panel. Comput Mech 53(4): 549-560.
12. Diaz CG, Vivolo M, Pluymers B, Vandepitte D, Desmet W (2010) Transmission suite design for vibro-acoustic. ISMA,pp. 2117-2130.
13. Jacobsen F (2011) The Sound Field in a Reverberation Room. Lect Note No 31261 Adv Acoust.
14. Gilford CLS (1959) The acoustic design of talks studios and listening rooms. Proc IEE - Part B Electron Commun Eng 106: 245-256.
15. Schmalle H, Noy D, Feistel S, Hauser G, Ahnert W, et al. (2011) Accurate Acoustic Modeling of Small Rooms. 131th Conv. Audio Eng Soc, USA, pp. 1-8.
16. Kuttruff KH (2008) Sound Propagation in Rooms. Handb. Noise Vib Control, USA, pp. 52-66.
17. Rivet E, Boulandet R, Lissek H, Rigas I (2012) Study on room modal equalization at low frequencies with electroacoustic absorbers 23-27.
18. Formisano A, Iazzetta G, Marino G, Fabbrocino F, Landolfo R (2016) Seismic residual capacity assessment of framed structures damaged by exceptional actions. ECCOMAS Congr. 2016 - Proc. 7th Eur. Congr. Comput Methods Appl Sci Eng 3: 4942-4958.
19. Fabbrocino F (2016) Estimation of the natural periods of existing masonry towers through empirical procedure. Int J Sustain Mater Struct Syst 2: 250.
20. Sarhosis V, Milani G, Formisano A, Fabbrocino F (2018) Evaluation of different approaches for the estimation of the seismic vulnerability of masonry towers. Bull Earthq Eng 16(3): 1511-1545.
21. Formisano A, Chieffo N, Monaco D, Fabbrocino F (2016) On the influence of the aggregate condition on the vibration period of masonry buildings: A case study in the district of Naples. AIP Conf Proc 1790.
22. Fabbrocino F, Titirla M, Amendola A, Benzoni G, Fraternali F( 2017) Innovative devices for the base isolation of existing buildings. COMPDYN 2017 - Proc. 6th Int. Conf. Comput. Methods Struct. Dyn Earthq Eng 2.
23. Cecchini F, Fabbrocino F, Nanni F (2017) Vibroacoustic response of a sandwich panel with a shear-thickening core. In: Hui D, editor. Compos Eng ICCE-25, Rome, Italy, pp. 32
24. Veen J, Jian P, pranab s (2005) Standardized Test Procedures for Small Reverberation Rooms, pp.18-20.
25. Lyubchik Y, Kenyo H (2013) Model of acoustic and vibroacoustic information leakage through a glass window in a protected room 62: 21-23.
26. Pluymers B (2006) Wave based modelling methods for steady-state vibro-acoustics, Belgium.
27. Zou D, Crocker MJ (2009) Sound Power Radiated from Rectangular Plates 39: 25-39.
28. Fahy F, Gardonio P (2006) Sound and Structural Vibration 2, Netherlands, pp: 656.
29. Fischer C, Plummer CJG, Michaud V, Bourban PE, Månson JAE (2007) Pre- and post-transition behavior of shear-thickening fluids in oscillating shear. Rheol Acta 46(8):1099-1108.
30. Mahjoob MJ, Mohammadi N, Malakooti S (2009) An investigation into the acoustic insulation of triple-layered panels containing Newtonian fluids: Theory and experiment. Appl Acoust 70(1): 165-171.
31. Mohammadi N, Mahjoob MJ (2009) Transmission loss of multilayer panels containing a fluid using progressive wave model : Comparison with impedance progressive model and experiments. C R Mec 337(4): 198-207.
32. Cecchini F, Cherubini V, Sadaf M, Fabbrocino F, Nanni F (2018) Design of a puncture-resistant composite shell comprising a non-Newtonian core. Polym Test 67: 494-502.
33. Larbi W, Deü JF, Ohayon R (2015) Vibroacoustic analysis of double-wall sandwich panels with viscoelastic core. Comput Struct 174: 92-103.
34. Amichi K, Atalla N, Ruokolainen R (2010) A new 3D finite element sandwich plate for predicting the vibroacoustic response of laminated steel panels. Finite Elem Anal Des 46(12): 1131-1145.
35. Loredo A, Plessy A, El Hafidi A, Hamzaoui N (2011) Numerical vibroacoustic analysis of plates with constrained-layer damping patches. J Acoust Soc Am 129(4): 1905-1918.
36. Corsaro RD, Sperling LH (1990) Sound and vibration damping with polymers. Sound Vib. Damping with Polym 424 : 5-22.