Peer Reviewed Chemistry Journals | Impact Factor Rankings

Metaheuristic Crafting of Organic Donor-Acceptor -Donor Copolymers

Priyanka Thakrala¹ and A K Bakhshi b²*

¹Department of Chemistry, St. Stephen's College, University of Delhi, India

²PDM University, Sir Shankar Lal Professor of Chemistry, India

Submission: July 03, 2017; Published: July 31, 2017

*Corresponding author: A K Bakhshi, Vice-Chancellor, PDM University, Harayana-124507; Email: akbakhshi2000@yahoo.com

How to cite this article: Priyanka T, A K Bakhshi b. Metaheuristic Crafting of Organic Donor-Acceptor-Donor Copolymers. Organic & Medicinal Chem IJ. 2017; 3(1): 555605. DOI: 10.19080/OMCIJ.2017.03.555605.

Abstract

Particle swarm optimization has been integrated with negative factor counting technique and inverse iteration method for efficient tailoring of binary low band gap donor-acceptor-donor copolymers. The structures investigated in this study include pyrrole and silole donor moieties in combination with carbonyl and dicyanomethylene acceptor groups respectively. A comparative examination of the electronic properties of all the possible donor and acceptor combinations has been done using the band structure results derived from ab-initio Hartree Fock crystal orbital calculations. The pyrrole-carbonyl donor-acceptor packaging is found to return lowest band gap combination. The DOS distributions of the investigated binary D-A-D

Copolymers give a similar qualitative picture of the trends in the electronic properties. Such a metaheuristic computational method efficiently returns optimized results worthy of synthetic trials.

Keywords: Copolymerization, Particle swarm optimization, Conducting polymers, Band gap, Computational chemistry, Meta-heuristic optimization, Donor-Acceptor Polymerizatio

Abbreviations: PSO: Particle Swarm Optimization; HOMO: Highest occupied molecular orbital; AI: artificial intelligence; DAD: donor-acceptor- donor

Introduction

The escalating need for smart and portable electronic devices has directed research towards development of sustainable, flexible and easy to handle and low on pocket conducting components of devices based on organic conjugated polymers [1-3]. Conducting polymers have found a variety of applications in electronic, medical, analytical and polymer technologies [4-7] because of their multifaceted assets which include low band gap, delocalized electronic backbone, redox activity, structural flexibility etc.

One driving force for polymer electronics is that their functionalities stem from the molecular skeletons rather than device structures [8,9]. The important electronic parameters that are used to characterize polymeric skeletons are band gap (Eg), HOMO (Highest occupied molecular orbital) energy positions and LUMO (Lowest unoccupied molecular orbital) energies positions [10-12]. Band gap (HOMO-LUMO energy gap) is an important device parameter that has been found to modulate in response to the structural variations in the polymer backbone [13-15]. Fine tuning of the band gap is important for device optimization as it dictates their electrochemical, optical and charge transport properties.

One efficient approach for band gap engineering is copolymerization [16,17]. Copolymerization is nothing but a combination of two or more repeat units that make up the polymer backbone. Copolymers can be built in a number of ways depending on the number (and type) of components and their connectivity in the polymer backbone. Since for a given copolymer combination, a large number of combinations are possible which differ in number and arrangements of repeat units in the chain, there is a considerable challenge in finding how best to couple the statistical nature and the properties of the combining components. Experimental as well as theoretical analysis of all possible combinations for a given copolymer assembly is a laborious task. Even systematic computational analysis is complex. Consequently, the development of efficient predictive methods to evaluate the candidates with respect to properties has gained urgency that save time and money without compromising accuracy, thereby returning optimized results. To blueprint copolymer combination with best structure-property correlation, we have developed an in-silico procedure based on metaheuristic artificial intelligence (AI) algorithm, viz, particle swarm optimization (PSO). PSO algorithm is a swarm intelligence technique where the central idea is "social adaptation of knowledge” motivated by bird flocking and fish schooling in search for food. PSO proposed by Kennedy and Eberhart in 1995 has been used extensively for solving a variety of complex nonlinear optimization problems [18,19]. In this urge to design copolymers with optimized electronic properties, PSO algorithm provides a rational course minimizing extensive manual effort and guiding experimentalists towards optimized results.

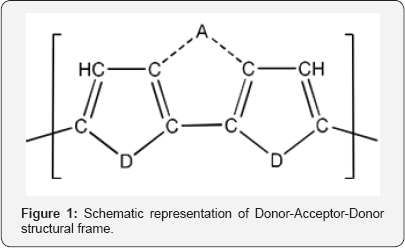
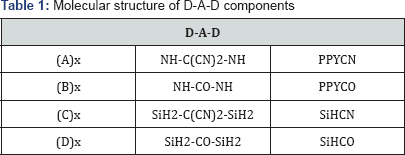
The molecular structures considered in this study are based on donor-acceptor-donor (D-A-D) framework. The donor- acceptor band gap engineering strategy was proposed by Havinga et al. in 1993 where he showed that the band gap can be narrowed or widened on the basis of the choice and design of donor and acceptor moieties or more correctly on the basis of the difference in electron density between the donor and acceptor units along the polymer backbone [20-22]. In this work, we have considered donor moieties based on pyrrole and silole. The intermediate acceptor units considered are dicyanomethylene group (>C-(CN) 2) and carbonyl group (>C=O) respectively

Conjugated polymers with thiophene / pyrrole as electron donating groups and cyano substituted acceptor group have been synthesized and reported to have band gap values in the range 1.6-2.7 eV [23] due to enhanced quinoid character and extended π-conjugation in the D-A-D backbone [24]. Density functional theory calculations on various thiophene / pyrrole donor-acceptor structures reveals -cyano and -hydroxy substituted donor-acceptor skeletons to have better intramolecular charge transfer abilities imparting good transport properties to the materials [25]. Silole based materials have found utility in opto-electronic devices24. Polypyrrole because of its facile functionalization and environmental stability have been used for biosensors6. Keeping in mind, the utility of these materials in various electronic mechanisms, in this work, we have investigated the electronic properties of binary D-A-D copolymer combinations to return potent donors, acceptors and donor-acceptor combination using PSO algorithm [26-28].

The structural skeleton of D-A-D unit considered in this work is shown in Figure 1, where the acceptor unit A is sandwiched between two heterocyclic donors at β-β' positions (as the β positions in these heterocyclic structures have larger n donating capacities than the α positions). The combinations of donor- acceptor units which are investigated in this study are shown in Table 1.

Methodology

The principle objective of this study is to craft the molecular codes of binary copolymers that correspond to optimal electronic properties. The aim of this investigation is to determine relative percentage compositions x% and y% of the constituent units A and B in the binary copolymer (AxBy)l respectively (where l = chain length / (x + y)) that correspond to minimum band gap value and maximum conducting ability such that the condition imposed x + y =100 is always satisfied. The relative percentage compositions x% and y% of constituents in the copolymer chain can take up integer values because of which we have employed the binary version of PSO algorithm viz., binary particle swarm optimization28, where the respective composition values in binary number form convert to integer values following a certain set of operations. The PSO algorithm maintains a swarm of particles which with limited individual intellect interacts locally among themselves and with their environment without any central supervision resulting in emergence of intelligent global and self-organized behavior.

To tailor low band gap copolymers, PSO algorithm [28] is integrated with two numerical methods, namely, negative factor counting technique (NFC) [29] and inverse iteration method (IIM) [29,30]. The PSO algorithm is initiated with a randomly generated swarm of particles. Each particle is represented in binary number form (in bits 0 and 1) (binary PSO) which on conversion gives integer numbers representing initial particle position (values of p, q, r and s) and velocity. Each particle position represents the relative percentage composition of the respective components corresponding to which a copolymer chain of 300 units is generated using a quasi-random function [31]. For every copolymer chain, the Huckel determinant is built up taking nearest neighbor

Interactions into account. A tridiagonal matrix is obtained with a's and P's as the diagonal and off-diagonal elements respectively and A's as the eigen values. Using NFC technique, eigen values are computed to obtain ionization potential (IP), electron affinity (EA) and band gap (Eg) values. IIM is used to return eigen vectors (coefficients Civ) of interest to compute inverse participation number (IPN, Ii) [32] which is a measure of the extent of delocalization of a MO in the polymer chain.

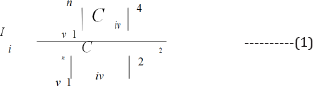
For each particle, the fitness function is evaluated. Fitness function is the only connecting link between algorithm and problem and therefore has to be appropriately adjusted. For the problem of designing low band gap copolymers, the fitness function is formulated as:

This gives equal statistical weight to band gap and IPN values respectively [33]. The properties so selected to test the fitness of particles are appropriately adjusted and therefore Eg is scaled using a constant 'ρ' which is taken as the difference between highest occupied energy level of the Valence Band and lowest unoccupied energy level of the Conduction Band amongst the combining constituents for a given copolymer system.

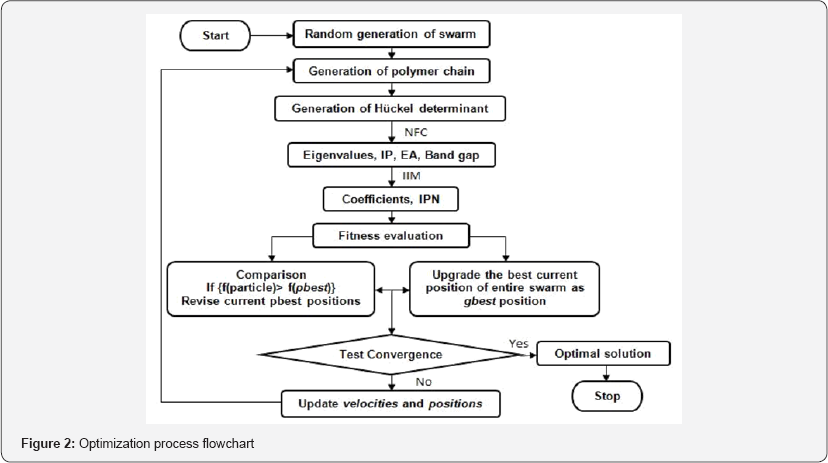
Once the fitness of the entire swarm is evaluated, a fitness comparison is performed for each particle between its current and previous solutions, storing the best amongst the two as particle's pbest (personal best) position. Another comparison is performed between the pbest positions of all the particles in the swarm, storing the best amongst the entire swarm as gbest (global best) position. The search is terminated by specifying a fixed number of iterations over which the gbest solution remain un-changed; else a new swarm is generated using the update rules cumulating pbest positions, gbest positions and velocity data. The new positions obtained are then evaluated with the constraint of not allowing the particles to revisit any position in its entire cycle. This constraint improves the exploration ability of the algorithm making each particle explore more solution space and upgrade pbest positions which in turn influence the gbest data. To further enhance the efficiency of the methodology, a boundary condition is specified which functions to draw back the particles to their upper and lower limits (based on the condition x + y =100), if they tend to explore beyond the specified limits. The execution of this PSO algorithm for efficient tailoring of low band gap polymers takes place in the manner shown in Figure 2. The detailed procedure and choice of various parameters used in this computational optimization has been discussed in our earlier study [27,33].

To determine the electronic density of states (DOS), we consistently used an energy grid of 0.001eV in all the calculations. The relative band alignments of the combining components of respective D-A-D copolymers are shown in Figure 3. The D-A-D band structures used in our calculations have been obtained from ab-initio Hartee-Fock Crystal orbital method using Clementi's 7s/3p minimal basis set [34].

Results and Discussion

In this work, we tailored different binary D-A-D copolymers and analyzed the effect of different donor-acceptor combinations on the electronic properties of the D-A-D copolymers using a computational scheme based on PSO algorithm. The electronic properties (obtained using Koopman's theorem) viz., IP, EA and Eg corresponding to the optimal copolymer compositions obtained by PSO algorithm are reported in Table 2.

IP value measure of electron donating ability of the chemical backbone and corresponds to the top of VB. A lower IP value is indicative of good electron donating capacity of the polymer or in other words, the structure becomes more labile towards p-doping. EA value is indicative of the electron attracting ability of the polymeric skeleton and corresponds to the bottom of the CB. A higher EA value results in better electron accepting character of the polymer or in other words, more is the inertia towards n-doping. The Eg value determines the intrinsic conducting ability of the polymer backbone. The lower the band gap value more is the conduction character of the macromolecular skeleton. The purpose of this study is to design the molecular codes of D-A-D copolymers corresponding to low IP, high EA and low Eg.

The copolymer B1 is a combination of PPYCN-SiHCN. The optimized composition (A86C14) returned by PSO indicates that a higher percentage of component A in the copolymer results in a low band gap copolymer conferring high intrinsic conductivity. This combination gives IP value (8.055 eV) in the region of HOMO of PPYCN and EA value (3.801) in the region of SiHCN. This indicates that pyrrole based structure is a better donor in comparison with silole based structure. Also, the optimized composition obtained contains a higher percentage of low IP value components, i.e., pyrrole backbone, making the polymer labile towards p-doping.

The other combination of PPYCN-SiHCO results in copolymer B2 for which the optimal solution (A92D8) again contains maximum amount of pyrrole based D-A-D component. Again, the IP value (8.054 eV) in the vicinity of HOMO of PPYCN and EA value (2.920) in the region of SiHCO. The copolymer B3 is a combination of PPYCO-SiHCN for the optimized composition is obtained as B73C27, again with higher percentage of pyrrole based skeleton. The combination of PPYCO-SiHCO gives optimized copolymer B4 composition as B64D36.

The cumulative study of these systems reveals that pyrrole is a better donor in comparison to silole based skeleton. And also the presence of higher percentage of pyrrole backbone not only results in lowering of band gap but also amplifies the ability of the polymer towards p-doping. Further, the IP values obtained indicate that PPYCO has better donating ability in comparison to PPYCN. If we analyze the optimized results and the corresponding EA values, it is found that dicyanomethylene based silole skeletons have higher EA values in comparison to carbonyl structures. This indicates silole and dicyanomethylene combination results in better donor-acceptor coupling in comparison to silole-carbonyl D-A-D coupling.

On analysis of the optimized results obtained from PSO algorithm, we find that the binary combinations comprising of component PPYCN (A) (Copolymers B1 and B2 respectively) have a major percentage of this component in comparison to the other combining components. However, the copolymers containing PPYCO

(B) (Copolymers B3 and B4 respectively) do contain a higher percentage of PPYCO but in comparison to copolymers B1 and B2 respectively, the amount of the other combining components in B3 and B4 is comparatively higher. The D-A-D copolymer combination with the lowest band gap obtained is that of PPYCO-SiHCN (Copolymer B3).

The DOS distribution curves obtained for all the binary D-A-D copolymers corresponding to the optimized solutions are shown in Figure 4 which consists of fine peaks as the units in the copolymer sequence are randomly arranged because of which the neighboring environment of each respective unit is not fixed and changes randomly The results obtained from DOS curves are in good agreement with the PSO results.

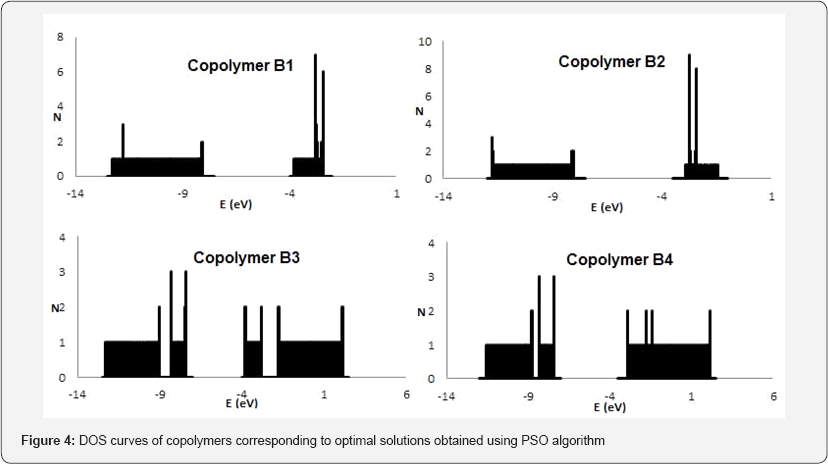
The IPN values prognostic of electronic delocalization in the polymer backbone, so computed for the PSO optimized results, indicate extensive delocalization in all the copolymer structures. Though extensive delocalization is observed from results in all the structures but copolymers with higher percentage of pyrrole skeleton have lower IPN values. And with increase in proportions of silole based backbone, increase in IPN value is observed. Nonetheless, extensive delocalization is observed in all the copolymer combinations.

On the whole, we can say that, the nature of the donor and acceptor moieties have statistically equal influence on the HOMO and LUMO energies of the copolymer backbone. Also, the nature of the heteroatom has a prominent control over the electronic band structures and conducting abilities of copolymers. In general, the low band gap compositions so obtained accommodates higher proportion of pyrrole based D-A-D structures. This is indicative of the relatively high donor strength of pyrrole group in comparison to silole based structures. All the copolymer combinations have lower band gap in comparison to the combining parent components which means that copolymerization results in enhanced intrinsic conductivity in all the structures.

Conclusion

In this study, we have investigated binary copolymers based on D-A-D framework using PSO algorithm. The optimized relative percentage compositions of D-A-D constituents in the respective copolymers so returned by PSO algorithm optimally qualify the fitness criterion so defined (low band gap value and extended n-conjugation in the copolymer backbone). A comparative study of electronic properties of all possible D-A-D copolymer combinations is inferred.

The trends in the electronic properties of the respective D-A-D copolymers so investigated in this study reveal the strong electron donating abilities of pyrrole derived skeleton. This observation suggests that the pyrrole derived donors can effectively be used for designing heterojunction photovoltaic devices and biosensors (which require low band gap components). The fusion of carbonyl acceptor onto the pyrrole skeleton in D-A-D model is found to deliver low IP values in the respective copolymers than the dicyanomethylene analogue.

The copolymers with the combination of pyrrole donor and carbonyl acceptor as one component returned lowest band gap configuration in comparison to the rest of the combinations due to enhanced n-delocalization in the polymer backbone imparting better charge transport properties. In all, we conclude that a higher relative percentage of PPYCO is highly desirable for designing low band gap materials. The best D-A-D copolymer combination obtained in this study is of PPYCO-SiHCN. The DOS distributions of the investigated binary D-A-D copolymers give a similar qualitative picture of the trends in the electronic properties.

The copolymerization scheme so adopted fine tunes the band gaps of D-A-D copolymers to lower values in comparison to the respective combining constituents. From these systems, the copolymers comprising of PPYCO component are found to be the strongest candidates for p-doping while those composed of SiHCN are found sturdiest for n-doping.

The results obtained indicate the potency of this in-silico methodology viz., PSO algorithm employed for investigating the influence of donor and acceptor groups on electronic properties of the copolymers. Adaptation of PSO algorithm helps simplify this compositional choice of building blocks of copolymers enabling fine tuning of band gap. Such a methodology is not only computationally cost effective but also labor and time saving without compromise on accuracy.

Investigations are being carried out using PSO algorithm to design intrinsically low band gap copolymers examining some other important classes of donor and acceptor groups for applications in medical and environmental analysis which are of utmost concern across the globe. Such an in-silico methodology can help channelize synthetic efforts by providing a judicious choice of potent donor-acceptor pairs for molecular engineering of efficient low band gap materials.