Peer Reviewed Chemistry Journals | Impact Factor Rankings

Research Article

The Application of Some Computing Techniques in the Drug Design

Nazmul Islam¹* and Savas Kaya²

¹Department of Basic Science & Humanities/ Chemistry, Govt. Engineering College Ramgarh, India

²Department of Chemistry, Cumhuriyet University, Turkey

Submission: April 26, 2017; Published: June 02, 2017

*Corresponding author: Nazmul Islam, Department of Basic Science & Humanities/ Chemistry, Govt. Engineering College Ramgarh, Jharkhand, India, Tel: + 91.9432878737 Email: nazmul.islam786@gmail.com

How to cite this article: Nazmul I & Savas K. The Application of Some Computing Techniques in the Drug Design.Organic & Medicinal Chem IJ. 2017; 2(5): 555596. DOI: 10.19080/omcij.2016.02.555596

Abstract

Using global and local reactivity descriptors of DFT and MO theory, in this work, we obtained a nice correlation between theoretically computed and experimentally determined drug activities (MIC). This study once again reveals the fundamental statement of theoretical chemistry that "the structure of a molecule determines its electronic wave function which in turn determines many of its physicochemical properties”. It is reasonable to suppose that the biological activity of molecules its potency as a drug for examples will also, often enough, be dependent upon the molecular electronic wave function. It is possible in principle to determine any molecular property that is ultimately dependent upon the molecule's electronic ground state wave function. In practice this can sometimes be achieved using rigorous procedures.

Abbreviations: QSAR: Quantitative Structure Activity Relationship; QC: Quantum-Chemical; EHT: Extended Huckel Theory; CNDO: Complete Neglect of Differential Overlap; INDO: Intermediate Neglect of Differential Overlap; MINDO: Modified Intermediate Neglect of Differential Overlap; MNDO: Modified Neglect of Diatomic Overlap; AM1: Austin Model 1; PM3: Parametric Model 3; RHF: Restricted Hartree-Fock level.

Introduction

Years of cumulative research can result in the development of a clinically useful drug, providing either cures from a particular disease or symptomatic relief form a physiological disorder. A dug, with a diseased pharmacological activity may have associated with some undesirable side effects which limits its' use. Current research reveals that the function of a drug may associate with its structural features. Computational theoretical chemistry is a branch of chemistry that uses theoretical studies to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids. While its results normally complement the information obtained by chemical experiments, it can in some cases predict hitherto unobserved chemical phenomena. It is widely used in the design of new drugs and materials.

Now a day, the synthesis of novel pharmacologically active molecules with reduced toxicity is of prime interest. Recently, QSAR has gained importance in the field of pharmacological sciences [1]. Quantitative structure Activity relationships (QSAR) are predictive tools for a preliminary evaluation of the activity of chemical compounds by using computer-aided models. The computational chemist can assist the experimental chemist or it can challenge the experimental chemist to find entirely new chemical objects.The Hohenberg and Khon theorm based DFT [2-4] provide a major boost to the computational chemistry The performance of DFT method in description of structural, energetic and magnetic molecular properties has been reviewed quite substantially in recent time.

DFT methods are in general capable of generating a variety of isolated molecular properties [5-12]. The commercial exploitation of organic compounds as a medicinal drug for examples is likely to require, at some stage of its development, the determination of biological or chemical activities or properties related to the intended end use of the compound. It is desirable therefore to have at hand relatively straightforward and inexpensive procedures enabling the efficient and accurate prediction of a molecular activity or property especially when its direct measurement by experiment is, for one reason or another, to be avoided if at all possible. The procedures that are conventionally used for indirect determinations of activities make use of molecular “descriptors” which include suitable molecular properties and physical-organic constructs obtained from both experimental and computational sources. Molecular descriptors are ultimately related to molecular structure. Hence the relationships between activities and the descriptors on which they depend are generally known as Quantitative Structure- Activity Relationships (QSARs) or Quantitative Structure- Property Relationships (QSPRs) depending upon whether the property of interest is to be characterized as biological or nonbiological, respectively.

The structure of a molecule determines its electronic wave function which in turn determines many of its physicochemical properties. It is reasonable to suppose that the biological activity of molecules its potency as a drug for examples will also, often enough, be dependent upon the molecular electronic wave function. It is now possible to perform accurate ab initio calculations routinely on molecules of moderate size at reasonable cost. Thus, it would clearly be advantageous to have available a procedure for estimating a molecular activity or property from descriptors which are derived from, and in turn characterize, the electronic wave function of a molecule.

It is possible in principle to determine any molecular property that is ultimately dependent upon the molecule's electronic ground state wave function. In practice this can sometimes be achieved using rigorous procedures. It can, for instance, be achieved for certain properties using quantum-mechanical expectation values. But when rigorous procedures are difficult or virtually impossible then it is necessary to use either a less rigorous model calculation or to use the Quantitative structure- activity relationship or Quantitative structure-property relationship methods.

Quantitative structure-activity relationship (QSAR) techniques increase the probability of success and reduce time and cost involvement in drug discovery process [13,14]. In this work, a correlation between the DFT descriptors and the drug activity of the Benzo[f]quinazolin-1(2H)-ones has been discussed. The aim of the present work is to explore the efficacy of the DFT based descriptors to provide some relationship by which the biological activity of hypothetical molecule can be measure prior to their synthesis. This technique shall reduce the drug discovery coast, time and efforts. In recent year heterocyclic compounds analogues of benzothaizoles and derivatives have attracted strong interest due to their useful biological and pharmacological properties. The chemistry of quinazolinones is interested because of its biological significance. Many of them shows antifungal [15], antibacterial [16], anticancer[17] anti- inflammatory[18] anticonvulsant [19] and antiproliferative activities as well as inhibitory effects for thymidylate synthase and poly-(ADP-ribose) polymerase (PARP) [20]. Quinazolin- 1-one derivatives are also found to be tranquilizer, antiallergic agent, an antiulcer agent and antiasthmatic agent.

Quantum-chemical (QC) calculations are a key element in biological research [21]. When constantly tested for their range of validity QC methods provide a description of how molecules interact and form their three-dimensional shape, which in turn determines molecular function. They can aid the formulation of hypotheses that provide the connecting link between experimentally determined structures and biological function. QC calculations can be used to understand enzyme mechanisms, hydrogen bonding, polarization effects, spectra, ligand binding and other fundamental processes both in normal and aberrant biological contexts. The power of parallel computing and progress in computer algorithms are enlarging the domain of QC applications to ever more realistic models of biological macromolecules.

The key insight of chemistry is the relationship between molecular structure and molecular function. We use the details of molecular structure to predict the properties of molecules. Medicinal chemistry is a particularly glaring example of our use of structure-function relationships. There is a tremendous need to be able to quickly design new drugs for curing human disease. The rapid prediction of the activities of compounds for use as drugs and the discovery of new compounds is an important goal. Quantitative Structure Activity Relationships, or QSAR [22] enables us to predict the properties of compounds and are a quantitative expression of structure-function relationships. QSAR has been responsible for the rapid development of many new drugs.

An example of a QSAR study is the narcotic activity of esters, alcohols, ketones, and ethers with tadpole. In this study various organic compounds were added to water with swimming tadpoles. The swimming speed of the tadpoles was observed and the amount of the compound that was necessary to slow the tadpoles swimming was determined. A very effective compound has a very low concentration for the production of the desired effect. In QSAR studies we often like to have the more effective compounds have a higher "activity,” not a lower. Therefore, it is very common to transform the concentration for a desired effect, C, to an activity by:

A = log(1/C) (1)

The log(1/C) value increases with compound efficacy

The genesis of QSAR is from physical organic chemistry and linear free energy relationships. The first such studies were done by L. P. Hammett [23]. His goal was to uncover the effects of electronic structure on organic reactivity. A short discussion of his work will be instructive as we start to understand the foundations of QSAR. Hammett's first studies were to understand the effect of electron withdrawing and donating groups on the pKa's of substituted benzoic acids, Hammett first wanted to develop a descriptor that described inductive substituent effects. He compared the log Ka for a variety of substituted benzoic acids with the log K_aH for unsubstitued benzoic acid to define the substituent constant σ.

σ = log Ka - log KaH (2)

σ the Hammett constants for meta and para substituents. He then postulated that other properties, other than acidity, would be likewise effected by the same substituent effects, and that these other properties would follow the relationship

log (property) = ρ σ + cst (3)

In other words, the expected function was a linear relationship with the ρ inductive constant.

Hammett obtained the equation from the relationship between Gibbs free energy and the equilibrium constant for a reaction,

Δ _rG = - RT ln Keq (4)

Semi-empirical methods can be used to calculate quantum chemical descriptors [24]. A number of semi empirical methods have been developed over the last several decades. To name but some of the most popular extended Huckel theory (EHT) [25], complete neglect of differential overlap (CNDO) [26] intermediate neglect of differential overlap (lNDO),[27]modified INDO- (MINDO), [28]modified neglect of diatomic overlap (MNDO),[29] Austin model 1 (AM1), ),[30] and parametric model 3 (PM3) [31].

The density functional theoretical parameters

Given the electron density function p(r) in a chemical system (atom or molecule) and the energy functional E(p), the chemical potential, μ of that system having N number of electrons in equilibrium has been defined as the derivative of the energy with respect to the number of electrons at fixed molecular geometry

The chemical potential [32], μ, is given by

μ= [δE(p) / δp] (5)

The differential definition more appropriate to atomic system is

μ = [∂E / ∂N]v (6)

Then following Iczkowski and Margrave [33], Parr and Pearson [34] defined the electro negativity as the additive inverse of the chemical potential-

χ = - μ (7)

or, χ = - [∂E/∂N] v (8)

and the absolute hardness, η, as

η = 1/2[∂μ/∂N] v = 1/2[∂2E/∂N2)] v (9)

The softness is defined as inverse of hardness (S=1/η).

Parr and Pearson [34] invoking the calculus of finite difference approximation suggested the approximate and operational formulae of electro negativity and hardness as under

χ = (I + A)/2 (10)

η = (I - A)/2 (11)

where l and A are the first ionization potential and electron affinity of the chemical species. Pearson [35] proceeded further to evaluate I and A in terms of orbital energies of the highest occupied molecular orbital, HOMO and the lowest unoccupied molecular orbital, LUMO as

χ = (€HOMO -€LUMO)/2 (12)

η = (-€HOMO + -€LUMO)/2 (13)

The electrophilicity, w is a descriptor of reactivity that allows a quantitative classification of the global electrophilic nature of a molecule within a relative scale. Parr et al. [36] suggested that electro negativity squared divided by hardness measures the electrophilic power of a ligand its prosperity to "soak up” electrons.

Thus,

ω = μ2/2η (14)

It is further anticipated that electrophilicity,w should be related to electron affinity, because both w and electron affinity measures capacity of an agent to accept electrons. Electron affinity reflect capability of an agent to accept only one electron from the environment, whereas electrophilicity index measures the energy lowering of a ligand due to maximal electron flow between the donor and acceptor The electron flows may be either less or more than one. Thus the electrophilicity index provides the direct relationship between the rates of reaction and the electrophilic power of the inhibitors [37].

Fukui functions play a prominent role in the field known as conceptual Density Functional Theory (DFT). Parr and Yang [38] based on the original ideas of Fukui [39], introduced fukui function which reflect the response of a molecular system towards a change in the number of electrons (Ne) of the molecular system under consideration .The fukui functions is a measure of local reactivity and defined as:

f (r) = ( ∂ ρ (r) /∂N )v (15)

where ρ(r) is the electron density.

Parr et al. [38] gave us the statement "the preferred direction is the one with largest f(r) at the direction side" and their firm prediction was -

Governing electrophilic attack f- (r)= [ ∂ ρ (r) / ∂N]- v (16)

Governing nuclophilic attack f+ (r)= [ ∂ ρ (r) / ∂N] +v (17)

Governing nutral attack f 0(r)= [ ∂ ρ (r) / ∂N] 0v (18)

These three cases have μs> μr, μs< μr and μs~ μ'r.

A "frozen core" approximation reveals dρ = dρvalue in each case and therefore governing electrophilic attack, f- (r) ≈ ρ (HOMO) (r) (19 ),

governing nuclophilic attack, f+(r) ≈ ρ (LUMO) (r) (20 ),

and governing neutral attack, f 0(r) ≈ 1/2[ρ (HOMO) (r) + ρ (LUMO) (r)] (21).

Method of Computation

We have used semi-empirical computational procedure, AM1 [31] to compute the orbital energies (HOMO, LUMO). Side by side we have also adopted a sophisticated ab-initio quantum chemical calculation procedure to compute the orbital energies (HOMO, LUMO). To be more specific, the planar structure of each of the substituted biphenyls was drown on the programme ArgusLab4.0.1[40] and geometry optimization was carried out at the restricted Hartree-Fock level (RHF) using STO-3G minimal basis set to compute the orbital energies (HOMO, LUMO) using AM1 procedure[31]. The ab-initio values are obtained when geometry optimization of the planar structure of each of the substituted biphenyls were carried out at restricted HartreeFock level (RHF) using STO-3G minimal basis set on the Hyper Chem 8.06 software [41].

The Ionization energies and electron affinities are calculated using the Koopmans theorem. The hardness value was calculated using Parr and Pearson method [34]. The electrophilicity index was calculated using the Parr et al's formula [36]. HOMO and LUMO Eigen functions obtained in the AM1 calculations were used to compute the fukui functions using Parr et al formulae [38].

Results and Discussion

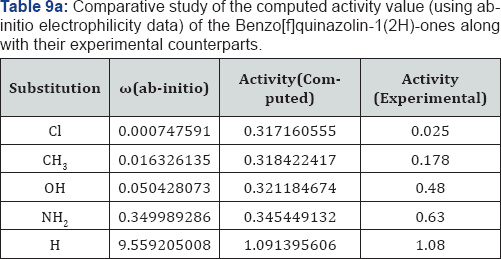
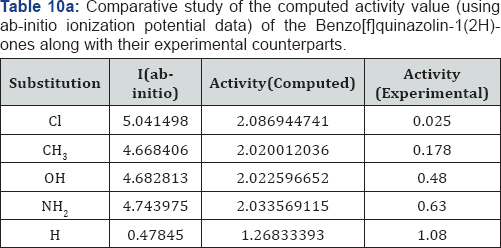
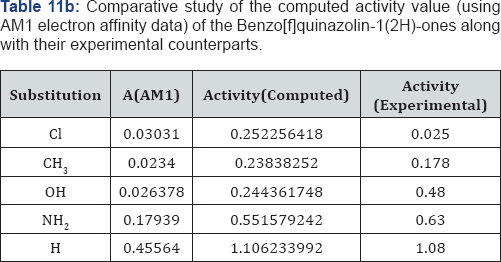
A look on the Tables 1a &1b reveal that, in both computational procedure-first principle and AM1, the ionization energy is maximum in the case of chloro substituted Benzo[f]quinazolin- 1(2H)-one and it is minimum in case of Benzo[f]quinazolin- 1(2H)-one. Further scrutiny of the table reveals that the electron affinity is maximum for NH₂ substituted Benzo[f]quinazolin- 1(2H)-one.and minimum for Benzo[f]quinazolin-1(2H)-one The electro negativity is maximum for Cl substituted Benzo[f] quinazolin-1(2H)-one and minimum for OH Benzo[f]quinazolin- 1(2H)-one. The hardness is maximum for Cl substituted and minimum f Benzo[f]quinazolin-1(2H)-one or OH substituted. The chemical potential is maximum for OH substituted Benzo[f] quinazolin-1(2H)-one Benzo[f]quinazolin-1(2H)-one.andminimum for H Benzo[f]quinazolin-1(2H)-one.

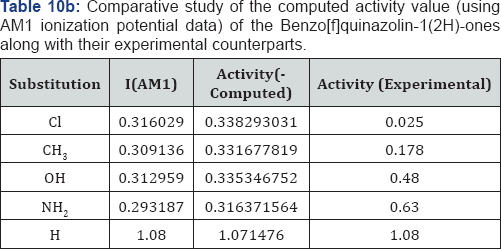
But we have surprisingly noted that the electro negativity value of all compounds studied by first principle on the minimal basis set STO-3G is negative. These do not agree with our normal experiences. We have thus adopted semi-empirical AM1 calculation on the same compounds. The semi-empirical results are discussed on the foregoing sections.

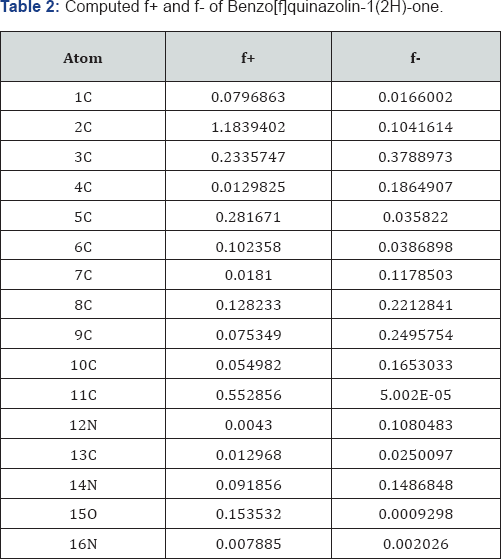
A look on Table 2 reveals that the centre 2C has the maximum f+ value and the centre12N has the minimum f+ value. Also it is found that the centrellC has the maximum f- value and the centre 15O has the minimum f- value in case of Benzo[f]quinazolin-1(2H)-one. A look on Table 3 reveals that the centre 4C has the maximum f+ value and the centre...17C has the minimum f+ value. Also it is found that the centre 3C has the maximum f- value and the centre 6C has the minimum f-value in case of Cl substitution Benzo[f]quinazolin-1(2H)-one.

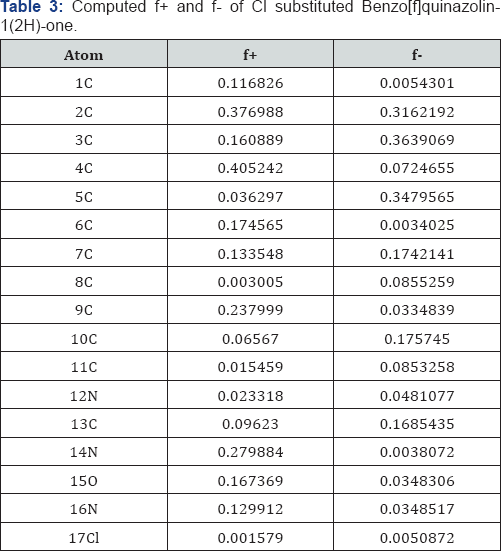
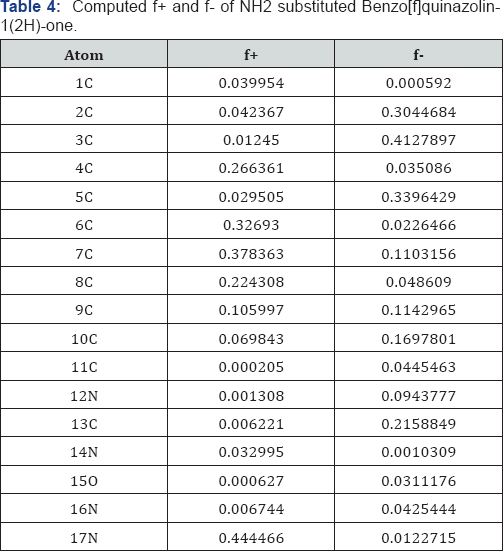
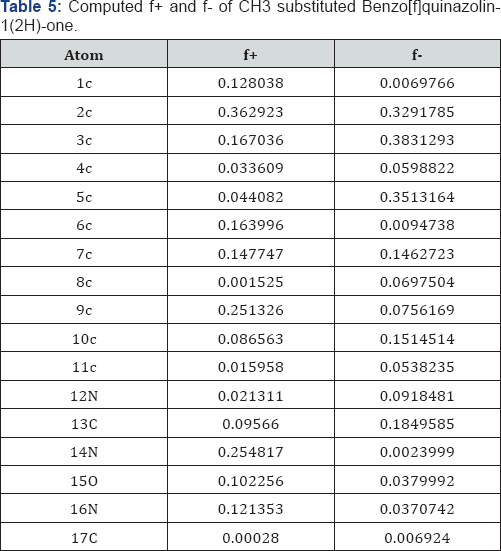
A look on Table 4 reveals that the centre 17N has the maximum f+ value and the centre 11C has the minimum f+ value. Also it is found that the centre 3C has the maximum f- value and the centre 1C has the minimum f-value in case of NH₂ substitution Benzo[f]quinazolin-1(2H)-one. A look on Table 5 reveals that the centre 2C has the maximum f+ value and the centre 8C has the minimum f+ value. Also it is found that the centre 3C has the maximum f- value and the centre 1C has the minimum f-value in case of CH₃ substitution Benzo[f]quinazolin-1(2H)-one .

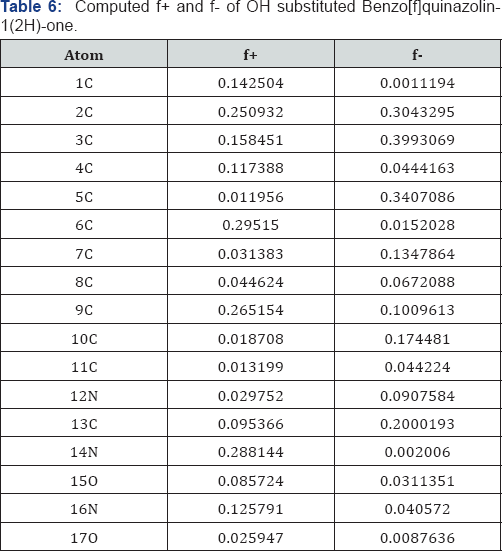
A deeper look on the Tables 3-6 reveals that the fukui functions on the different atoms of the molecules studied depends upon the substituents. The nucleophilic fukui functions of the 12 N atom varies in the following order- Benzo[f]quinazolin- 1(2H)-one OH->Cl>CH₃>H>NH₂ Benzo[f]quinazolin-1(2H)-one .The electrophilic fukui function of the 12 N atom varies in the following order- H>NH₂l>CH₃>Cl>OH Benzo[f]quinazolin-1(2H)- one .The nucleophilic fukui function of the 14 N atom varies in the following order- Cl>CH₃>OH>H>NH₂ Benzo[f]quinazolin- 1(2H)-one. The electrophilic fukui function of the 14 N atom varies in the following order- H>Cl>CH₃>OH>NH₂ Benzo[f] quinazolin-1(2H)-one. The nucleophilic fukui function on the 15 O atom varies in the following order-OH-Benzo[f]quinazolin- 1(2H)-one>Cl-Benzo[f]quinazolin-1(2H)-one>CH₃- Benzo[f] quinazolin-1(2H)-one >H- Benzo[f]quinazolin-1(2H)-one>NH₂- Benzo[f]quinazolin-1(2H)-one.

The electrophilic fukui function on the 15 O atom varies in the following order-CH₃ Benzo[f]quinazolin-1(2H)-one >Cl Benzo[f]quinazolin-1(2H)-one >OH Benzo[f]quinazolin-1(2H)- one >NH₂>H Benzo[f]quinazolin-1(2H)-one. The nucleophilic fukui function on the 16N atom varies in the following order-

Cl- Benzo[f]quinazolin-1(2H)-one> Benzo[f]quinazolin- 1(2H)-one>OH- Benzo[f]quinazolin-1(2H)-one >CH₃- Benzo[f] quinazolin-1(2H)-one> NH₂- Benzo[f]quinazolin-1(2H)-one. The electrophilic fukui function on the 16N atom varies in the following order-NH₂- Benzo[f]quinazolin-1(2H)-one>OH- Benzo[f]quinazolin-1(2H)-one>CH₃ Benzo[f]quinazolin-1(2H)- one >Cl- Benzo[f]quinazolin-1(2H)-one> Benzo[f]quinazolin- 1(2H)-one.

We have found a linear correlation between the global reactivity parameters of conceptual density functional theory and their drug activities.

We have correlated the global reactivity parameters of conceptual density functional theory with the drug activities of the Benzo[f]quinazolin-1(2H)-ones. We have found excellent correlation between the global hardness of the molecules and their drug activity.

Our suggested ansatz for the drug activity are‑

Drug Activity = ‐0.1289rηab‐initio + 1.1378 (22]

Drug Activity =‐0.1919 χab‐initio +0.3446 (23)

Drug Activity = 0.1919 μab-initio +.3446 (24)

Drug Activity = 0.081ωab‐initio + 1.3171 (25)

Drug Activity = 0.0086Sab‐initio + 0.3268 (26)

And using AM1 reactivity parameters

Drug Activity = ‐6.00386ηAM1 + 1.0789 (2 7)

Drug Activity =2.2924 χAM1 +0.1481 (28)

Drug Activity = ‐2.2924 μAM1 ‐0.1481 (29)

Drug Activity = 0.0894ωAM1 + 0.2604 (30)

Drug Activity = 0.0688SAM1 + 1.0789 (31)

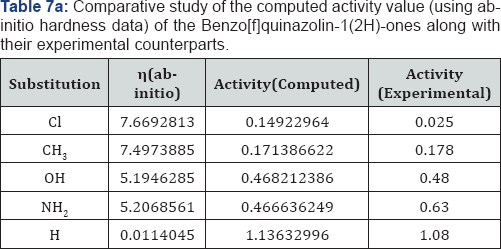
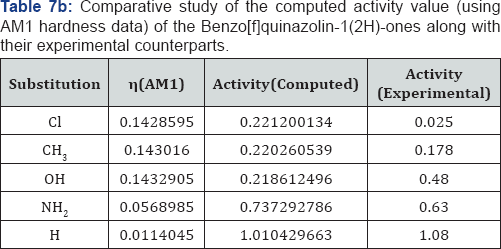
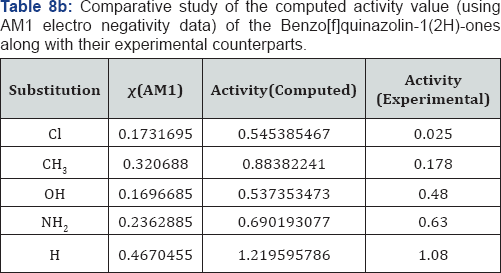
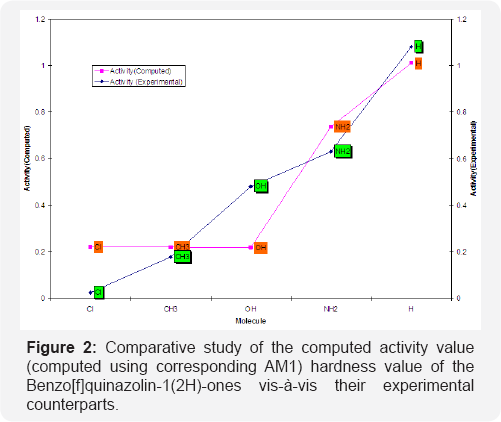
We have computed the drug activity of the Benzo[f] quinazolin-1(2H)-ones using the above ansatz 1,2 and 4 and 6,7 and 9 and presented them in Tables 6-12. As the chemical potential is the negative counterpart of electro negativity and the softness is the inverse of hardness only, we have not considered them for computing the activity value. A deep scrutiny of the Tables 6-12 reveal that the theoretical activity value correlate well with the experimental values. In the case of hardness, this correlation is the best among the reactivity parameters in both ab-initio and AM1 computed results. We have drown Figures 1 & 2 to explore the correlation between theoretical computed and experimentally determined drug activity value of the Benzo[f] quinazolin-1(2H)-one using ab-initio and semi empirical hardness values respectively. From Figures 1 & 2 we can see that the activity data of the four compound correlate excellently with the experimental values. In the case of AM1 hardness data excellent correlation found in two values and other values fairly correlate with the experimental data.

Conclusion

Using global and local reactivity descriptors of DFT and MO theory, we have found a nice correlation between theoretically computed and experimentally determined drug activities (MIC). The fukui functions and local softness's at different sites changes with the change in substituents. This study once again reveals the fundamental statement of theoretical chemistry that "the structure of a molecule determines its electronic wave function which in turn determines many of its physicochemical properties”. It is reasonable to suppose that the biological activity of molecules its potency as a drug for examples will also, often enough, be dependent upon the molecular electronic wave function. It is possible in principle to determine any molecular property that is ultimately dependent upon the molecule's electronic ground state wave function. In practice this can sometimes be achieved using rigorous procedures.